L I GI I THI UỜ Ớ Ệ
T p bài gi ng v “ T đ ng hoá thi t k tàu thu A1” do PGS.TS. Lê H ng Bangậ ả ề ự ộ ế ế ỷ ồ
– B môn Lý thuy t thi t k tàu th y khoa Đóng tàu Đ i h c Hàng h i Vi t Nam biênộ ế ế ế ủ ạ ọ ả ệ
so n nh m m c đích trang b cho các sinh viên h chính qui chuyên ngành Thi t k thânạ ằ ụ ị ệ ế ế
tàu th y m t s nh ng ki n th c c b n nh t v t đ ng hóa tính toán các y u t th yủ ộ ố ữ ế ứ ơ ả ấ ề ự ộ ế ố ủ
tĩnh và n đ nh c a các lo i tàu th y thông d ng. Bài gi ng này là m t b ph n c a giáoổ ị ủ ạ ủ ụ ả ộ ộ ậ ủ
trình v “T đ ng hóa thi t k tàu th y và công trình n i “ s ra m t b n đ c nay mai.ề ự ộ ế ế ủ ổ ẽ ắ ạ ọ
T p bài gi ng đ c chia thành 2 ph n: Ph n I mang tiêu đ “ PH NG PHÁP TÍNHậ ả ượ ầ ầ ề ƯƠ
TOÁN". Ph n này s gi i thi u vi c ng d ng ph ng pháp s đ gi i các bài toán v tầ ẽ ớ ệ ệ ứ ụ ươ ố ể ả ề ự
đ ng hóa tính toán các y u t th y tĩnh và n đ nh c a tàu th y bao g m đa th c n i suyộ ế ố ủ ổ ị ủ ủ ồ ứ ộ
Lagrange, ph ng pháp bình ph ng nh nh t, các ph ng pháp g n đúng đ tính các tíchươ ươ ỏ ấ ươ ầ ể
phân xác đ nh. Ph n II mang tiêu đ “ H NG D N S D NG ph n m mị ầ ề ƯỚ Ẫ Ử Ụ ầ ề
AUTOSHIP”. Do th i l ng c a môn h c có h n vì v y ph n này ng i biên so n chờ ượ ủ ọ ạ ậ ở ầ ườ ạ ỉ
t m d ng l i ch gi i thi u và h ng d n s d ng 3 module trong 5 module c a ph nạ ừ ạ ở ổ ớ ệ ướ ẫ ử ụ ủ ầ
m m nêu trên bao g m: AUTOSHIP; AUTOHYDRO và AUTOPOWER. Hai module cònề ồ
l i là ; AUTOPLATE và AUTOSTRUCTURE sinh viên s t nghiên c u áp d ng khi th yạ ẽ ự ứ ụ ấ
c n thi t b i l trong ph n hai c a “T đ ng hoá thi t k tàu thu A2” chúng tôi s t pầ ế ở ẻ ầ ủ ự ộ ế ế ỷ ẽ ậ
trung h ng d n s d ng ph n m m SHIPCONSTRUCTOR dành cho t đ ng thi t kướ ẫ ử ụ ầ ề ự ộ ế ế
công ngh mà trong đó có ch a hai Module có tính năng m nh h n AUTOPLATE vàệ ứ ạ ơ
AUTOSTRUCTURE trong AUTOSHIP. Riêng Ph n II c a T p Bài gi ng “T đ ng hoáầ ủ ậ ả ự ộ
thi t k tàu thu A1” s đ c in thành m t b riêng đ đ các sinh viên và các k sế ế ỷ ẽ ượ ộ ộ ủ ể ỹ ư
cũng nh các h c viên cao h c ngành K thu t tàu th y s d ng m t cách có hi u quư ọ ọ ỹ ậ ủ ử ụ ộ ệ ả
trong quá trình th c hi n các bài toán c th .ự ệ ụ ể
Đ h c và nghiên c u có hi u qu môn h c này ng i biên so n mong mu n b nể ọ ứ ệ ả ọ ườ ạ ồ ạ
đ c và các em sinh viên chuyên ngành Thi t k tàu th y hãy dành m t ph n th i gian đọ ế ế ủ ộ ầ ờ ể
ôn l i các ki n th c thu c ch ng trình toán cao c p dành cho k s , tham kh o các tàiạ ế ứ ộ ươ ấ ỹ ư ả
li u nói v ph ng pháp tính, tĩnh h c tàu th y, đ ng l c h c tàu th y, giáo trình toán ngệ ề ươ ọ ủ ộ ự ọ ủ ứ
d ng trong k thu t ....ụ ỹ ậ
Ng i biên so n xin bày t lòng bi t n chân thành đ i v i các ý ki n góp ý đ t pườ ạ ỏ ế ơ ố ớ ế ể ậ
bài gi ng này s ngày càng hoàn thi n h n c v n i dung l n ph ng pháp trình bày.ả ẽ ệ ơ ả ề ộ ẫ ươ
M i ý ki n góp ý xin b n đ c g i v cho tác gi theo đ a ch sau: B môn Lý thuy t thi tọ ế ạ ọ ử ề ả ị ỉ ộ ế ế
k tàu th y khoa Đóng tàu Đ i h c Hàng h i ho c E-Mail: ế ủ ạ ọ ả ặ lehbang@hn.vnn.vn.
TÁC GIẢ
1
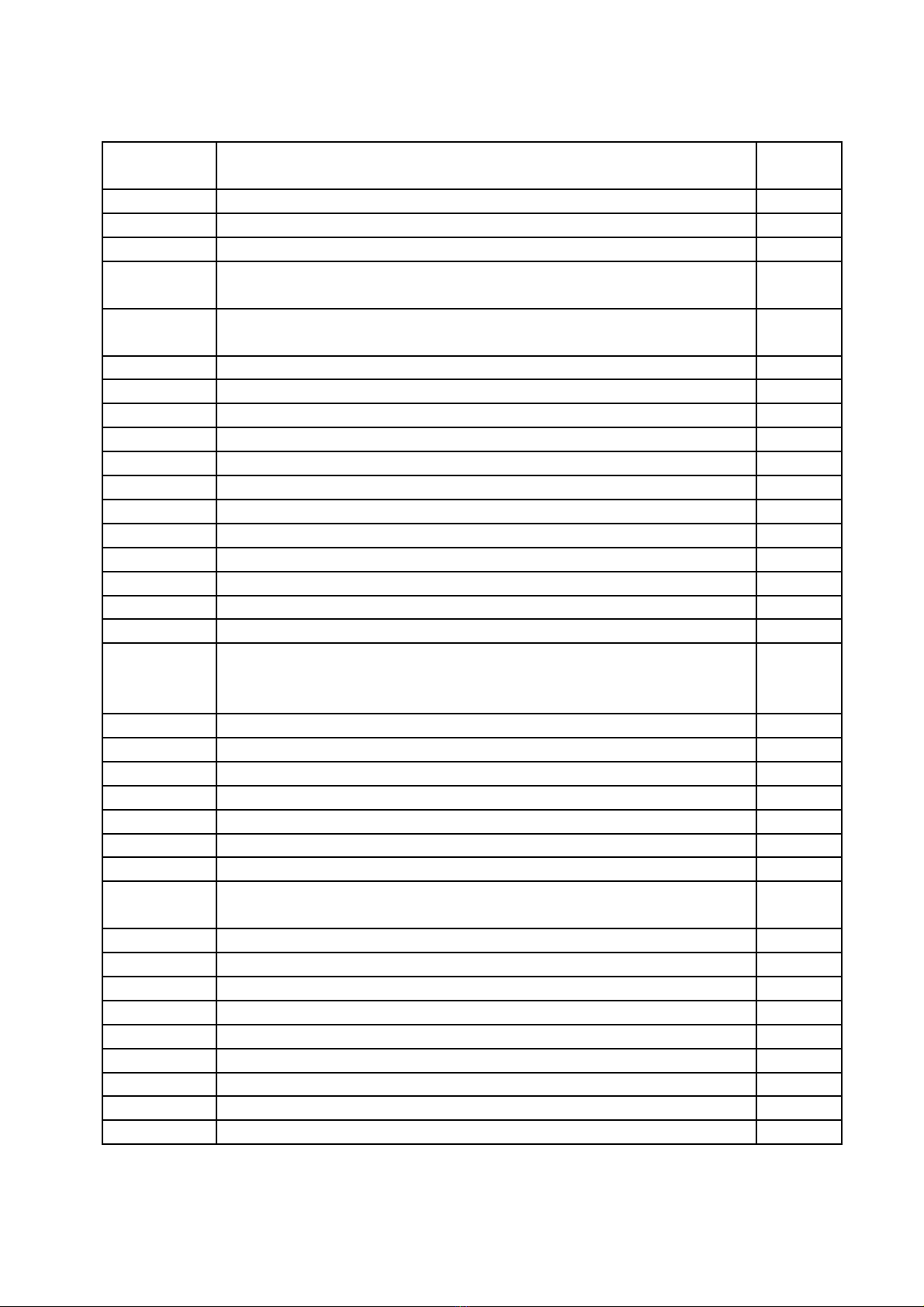
M C L CỤ Ụ
Ch ng ,ươ
m cụTên ch ng, m cươ ụ Trang
số
Ch ng ươ 1 NGÔN NG L P TRÌNH VÀ T Đ NG HOÁ THI T K Ữ Ậ Ự Ộ Ế Ế 4
1.1 Khái ni m v ngôn ng l p trìnhệ ề ữ ậ 4
1.2 Gi i thi u m t s ngôn ng l p trình đi n hìnhớ ệ ộ ố ữ ậ ể 4
Ch ng ươ 2 T Đ NG HÓA TÍNH TOÁN CÁC Y U T TH Y TĨNHỰ Ộ Ế Ố Ủ
VÀ TÍNH CÂN B NG- N Đ NH C A TÀUẰ Ổ Ị Ủ 9
2.1 Ph ng pháp s dùng trong t đ ng hoá tính toán các y u tươ ố ự ộ ế ố
th y tĩnh và tính cân b ng- n đ nh c a tàuủ ằ ổ ị ủ 9
2.1.1 Đa th c n i suy Lagrangeứ ộ 9
2.1.2 Ph ng pháp bình ph ng bé nh t ươ ươ ấ 13
2.2 Các ph ng pháp tính g n đúng tích phân xác đ nhươ ầ ị 15
2.2.1 Đ t bài toánặ15
2.2.2 Công th c hình thangứ16
2.2.3 Đánh giá sai số17
2.2.4 Ví dụ17
2.2.5 S đ tóm t tơ ồ ắ 18
2.2.6 Công th c Simsonứ19
2.2.7 Đánh giá sai số19
2.2.8 Ví dụ20
2.2.9 S đ tóm t t công th c Simsonơ ồ ắ ứ 20
2.3. ng d ng các ph ng pháp tính g n đúng tích phân xác đ nhỨ ụ ươ ầ ị
đ tính toán các y u t tính n i th y l c và n đ nh cho tàuể ế ố ổ ủ ự ổ ị
th yủ
21
2.3.1 Ph ng pháp hình thangươ 21
2.3.2. Ph ng pháp Simpsonươ 22
2.3.3 Ph ng pháp Tre-b -sevươ ư 25
2.4 Tính n i tàu thuổ ỷ 26
2.4.1 Tính các đ i l ng hình h c v tàuạ ượ ọ ỏ 26
2.4.2 T l Bonjeanỉ ệ 28
2.4.3 Th tích ph n chìm và các đ i l ng liên quan đ n th tíchể ầ ạ ượ ể ể 28
2.4.4 Bi n pháp nâng cao đ chính xác c a các ph ng pháp tíchệ ộ ủ ươ
phân g n đúngầ31
2.4.5 Tính các đ ng thu tĩnh trên máy cá nhânườ ỷ 35
2.4.6 Bi u đ mang tên Firsovể ồ 40
2.5 Cân b ng- n đ nh tàuằ Ổ ị 41
2.5.1 n đ nh ngang ban đ uỔ ị ầ 41
2.5.2 n đ nh khi tàu nghiêng góc l nỔ ị ớ 44
2.5.3 Đ th n đ nhồ ị ổ ị 46
2.5.4 Thu t toán xác l p h đ ng ậ ậ ọ ườ Pan-tô-ka-ren 51
2.5.5 D ng đ th n đ nh trên c s Pan-to-ka-renự ồ ị ổ ị ơ ở 53
TÀI LI U THAM KH OỆ Ả 54
2
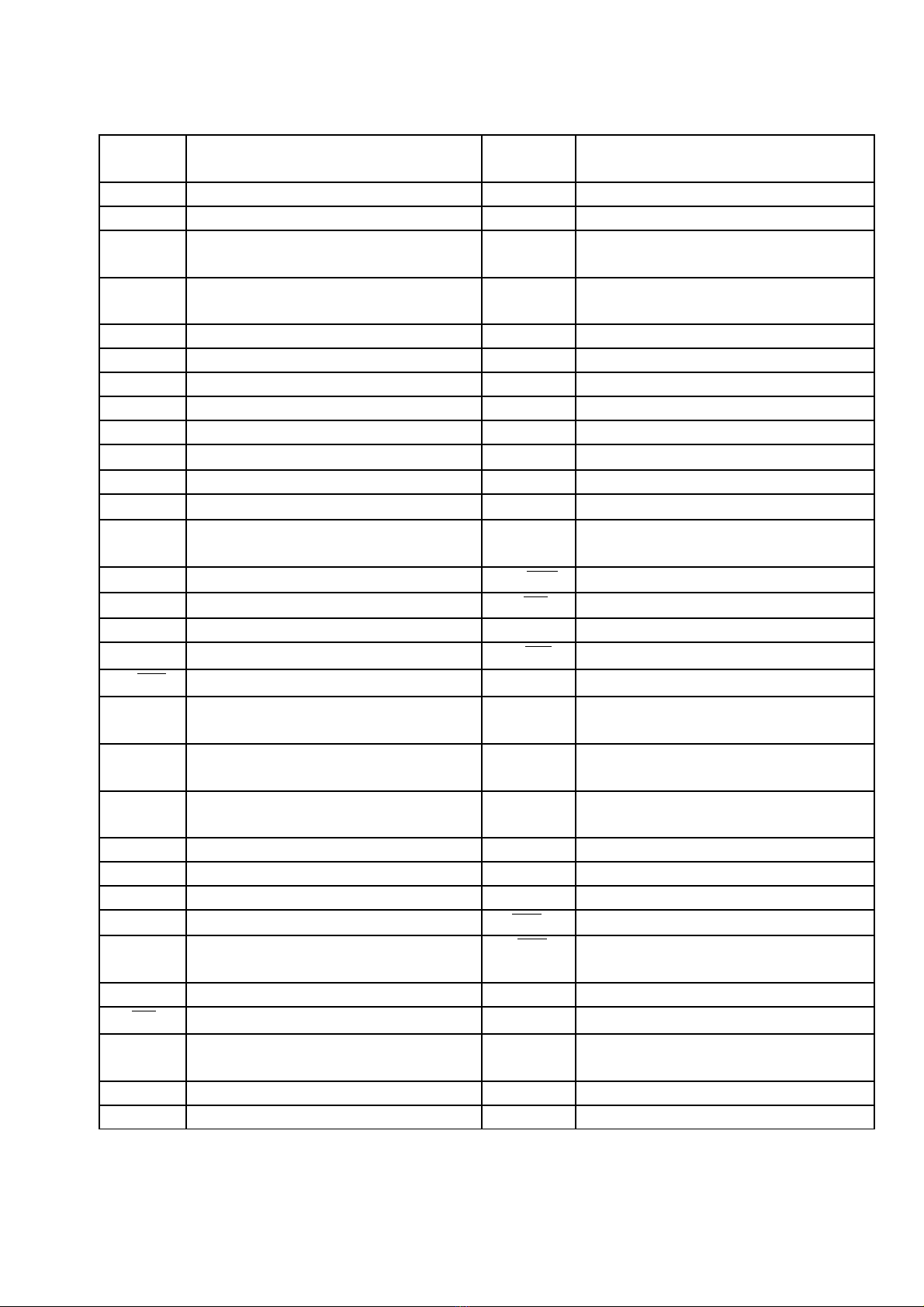
b¶ng ký hiÖu thêng dïng
Ký
hi uệTên g iọKý hi uệTên g iọ
AVDi n tích h ng gióệ ứ MTRIM Mô men chúi trên 1 cm
AWDi n tích m t đ ng n cệ ặ ườ ướ Mchf Mô men nghiêng cho phép
AMDi n tích m t s n gi aệ ặ ườ ữ M0y Mô men tĩnh di n tích m tệ ặ
đ ng n c đ i v i tr c 0yườ ướ ố ớ ụ
aKho ng cách t tr ng tâm đ nả ừ ọ ế
tâm n iổM0x Mô men tĩnh di n tích m tệ ặ
đ ng n c đ i v i tr c 0xườ ướ ố ớ ụ
BChi u r ng tính toánề ộ Mx0y Mô men tĩnh th tích đ i v i xoyể ố ớ
Bmax Chi u r ng toàn bề ộ ộ My0z Mô men tĩnh th tích đ i v i y0zể ố ớ
CBH s béo chungệ ố XGHoành đ tr ng tâmộ ọ
CMH s béo s n gi aệ ố ườ ữ XBHoành đ tâm n iộ ổ
CWH s béo đ ng n cệ ố ườ ướ XfHoành đ tr ng tâm đ ng n cộ ọ ườ ướ
CVH s béo th ng đ ngệ ố ẳ ứ θGóc nghiêng ngang c a tàuủ
CPH s béo d cệ ố ọ ψGóc chúi c a tàuủ
∆ L ng chi m n c tr ng l ngượ ế ướ ọ ượ YBTung đ tâm n iộ ổ
∆dKho ng cách gi a các đ ngả ữ ườ
n cướ yiN a tung đ đ ng n c kh oử ộ ườ ướ ả
sát ng v i s n th iứ ớ ườ ứ
∆LKho ng cách gi a các s nả ữ ườ ZM,
KM
Cao đ tâm nghiêng ngangộ
D, dChi u cao m n, Chi u chìmề ạ ề ZB,
KB
Cao đ tâm n iộ ổ
dθcánh tay đòn n đ nh đ ngổ ị ộ ZCCao đ tâm n iộ ổ
h Chi u cao tâm nghiêng ngangềZG,
KG
Cao đ tr ng tâmộ ọ
h0,
MG
Chi u cao tâm nghiêng ban đ uề ầ ZVCao đ tr ng tâm h ng gióộ ọ ứ
ITMô men quán tính di n tíchệ
đ ng n c đ i v i tr c d cườ ướ ố ớ ụ ọ ΩDi n tích m t s n kh o sátệ ặ ườ ả
ILMô men quán tính di n tíchệ
đ ng n c đ i v i tr c ngangườ ướ ố ớ ụ VTh tích l ng chi m n cể ượ ế ướ
I’LMô men quán tính di n tíchệ
đ ng n c đ i v i tr c 0ườ ướ ố ớ ụ ’- y’
VZTh tích ngâm n c ng v iể ướ ứ ớ
đ ng n c zườ ướ
kg H s cao đ tr ng tâm ệ ố ộ ọ SZDi n tích m t đ ng n c t i zệ ặ ườ ướ ạ
LChi u dài tính toánềmzMô men tĩnh di n tích m t s n ệ ặ ườ
Lmax Chi u dài toàn bề ộ CzTr ng tâm di n tích m t s nọ ệ ặ ườ
Lkwl Chi u dài đ ng n c thi t kề ườ ướ ế ế r,
BM
Bán kính tâm nghiêng ngang
LPP Chi u dài gi a hai đ ng vuôngề ữ ườ
góc R,
L
BM
Bán kính tâm chúi
Lk Cánh tay đòn n đ nh hình dángổ ị
lθ,
GZ
Tay đòn n đ nh tĩnh ổ ị
lchf Tay đòn mô men nghiêng cho
phép
Mhp Mô men h i ph cồ ụ
MVMô men nghiêng do gió tác d ngụ
3
Ch ng 1ươ
NGÔN NG L P TRÌNH VÀ T Đ NG HOÁ THI T KỮ Ậ Ự Ộ Ế Ế
1.1. KHÁI NI M V NGÔN NG L P TRÌNHỆ Ề Ữ Ậ
Ngôn ng l p trình là nh ng ph n m m đ phát tri n các ng d ng. Ngôn ng l pữ ậ ữ ầ ề ể ể ứ ụ ữ ậ
trình đã tr i qua quá trình phát tri n và không ng ng hoàn thi n, nó là công c quan tr ngả ể ừ ệ ụ ọ
đ i v i s phát tri n c a công ngh thông tin. T đ ng hoá tính toán, thi t k và hi n thố ớ ự ể ủ ệ ự ộ ế ế ể ị
k t qu tính đ u thông qua ngôn ng l p trình. Nh ng ngôn ng l p trình có ng d ngế ả ề ữ ậ ữ ữ ậ ứ ụ
r ng rãi và hi u qu có th nêu lên sau đây.ộ ệ ả ể
1.2. GI I THI U M T S NGÔN NG L P TRÌNH ĐI N HÌNHỚ Ệ Ộ Ố Ữ Ậ Ể
•FORTRAN (vi t t t t FORmula TRANslation) ra đ i t nh ng năm nămế ắ ừ ờ ừ ữ
m i, chính xác h n năm 1957, ng d ng ch y u trong các ngành khoa h c, k thu t.ươ ơ ứ ụ ủ ế ọ ỹ ậ
Phiên b n đ u c a FORTRAN th ng đ c nh c đ n v i tên g i FORTRAN II ,ả ầ ủ ườ ượ ắ ế ớ ọ
song phiên b n đ c dùng ph bi n nh t là FORTRAN IV. Các dàn máy IBM th i b y giả ượ ổ ế ấ ờ ấ ờ
nh n d ng phiên b n ph thông này d i tên vi t ghép FORTRAN. Ngôn ng thích h pậ ạ ả ổ ướ ế ữ ợ
cho vi c x lý nh ng bài toán c l n c a th i đ i, đ c dùng trong các ch ng trình tínhệ ử ữ ỡ ớ ủ ờ ạ ượ ươ
toán thi t k ô tô, tàu thu , máy bay, tính toán đ b n các công trình xây d ng, thi t k t iế ế ỷ ộ ề ự ế ế ố
u. Có th coi h n 90% nh ng ch ng trình l n trong các lĩnh v c khoa h c, k thu tư ể ơ ữ ươ ớ ự ọ ỹ ậ
đ c vi t b ng ngôn ng này.ượ ế ằ ữ
Th c t s d ng đã n y sinh vài v n đ phi n toái. Các nhà s n xu t các ch ngự ế ử ụ ả ấ ề ề ả ấ ươ
trình đa năng t cho phép mình vi t các b d ch cho FORTRAN theo s tr ng c a riêngự ế ộ ị ở ườ ủ
mình. Tuy ph n l n các nhà s n xu t v n d a vào tiêu chu n c a ANSI - Americanầ ớ ả ấ ẫ ự ẩ ủ
National Standards Institute đ biên so n compiler cho FORTRAN IV song ch ng có bể ạ ẳ ộ
d ch nào gi ng b d ch nào, vì ng i nào cũng c xé rào kh i chu n ANSI. Tình hình yị ố ộ ị ườ ố ỏ ẩ ấ
b t bu c ANSI ph i ra tay th ng nh t, năm 1978 phiên b n cu i cùng mang tên ANSI X3.9ắ ộ ả ố ấ ả ố
- 1978 đã đ t d u ch m cho s bùng phát t do. Phiên b n này có tên g i FORTRAN 77,ặ ấ ấ ự ự ả ọ
ngày nay đ c dùng t ng đ i r ng rãi.ượ ươ ố ộ
• Algol , vi t t t t Algorithm, ra đ i vào đ u nh ng năm sáu m i v i s thamế ắ ừ ờ ầ ữ ươ ớ ự
gia r t đông các nhà toán h c, nh ng ng i vi t ch ng trình c a châu Âu. Ngôn ngấ ọ ữ ườ ế ươ ủ ữ
đ c thi t k r t trong sáng, d h c, d th c hi n. Đây là phiên b n c a b môn toán tínhượ ế ế ấ ễ ọ ễ ự ệ ả ủ ộ
dùng trong máy tính. Ngôn ng thích h p cho vi c gi i quy t nh ng v n đ khoa h c c aữ ợ ệ ả ế ữ ấ ề ọ ủ
th i đ i. T t c các thu t toán chu n ra đ i trong th i kỳ này đ c chuy n thành ch ngờ ạ ấ ả ậ ẩ ờ ờ ượ ể ươ
trình vi t b ng Algol 60. Cho đ n cu i nh ng năm b y m i ch ng trình b ng ngôn ngế ằ ế ố ữ ả ươ ươ ằ ữ
Algol còn đ c ch y trên các dàn máy l n. Nh ng ch ng trình m u gi i quy t nh ngượ ạ ớ ữ ươ ẫ ả ế ữ
v n đ tính toán theo ph ng pháp s , đ c bi t ph n đ i s tuy n tính, vi t b ng Algol tấ ề ươ ố ặ ệ ầ ạ ố ế ế ằ ừ
nh ng năm sáu m i cho đ n t n ngày nay v n là nh ng ch ng trình u vi t, ch a gìữ ươ ế ậ ẫ ữ ươ ư ệ ư
thay đ c.ượ
4
Ngôn ng này là ngôn ng t t song không sinh ra t i M , có l đó là căn c đ gi iữ ữ ố ạ ỹ ẻ ứ ể ả
thích câu h i t i sao ngôn ng này không tìm đ c ch đ ng M , vi c này đ ng nghĩaỏ ạ ữ ượ ỗ ứ ở ỹ ệ ồ
v i s h n ch s ng i dùng và s phát tri n ti p theo.ớ ự ạ ế ố ườ ự ể ế
• COBOL (Common Business Oriented Language) ra đ i năm 1960, áp d ngờ ụ
ch y u trong lĩnh v c kinh doanh, th ng m i. Ngôn ng này đ c hoàn thi n và còn tìmủ ế ự ươ ạ ữ ượ ệ
th y ch đ ng t n hôm nay.ấ ỗ ứ ậ
•BASIC (vi t t t t Beginner's All-purpose Symbolie Instruction Code) doế ắ ừ
Kemeny và Kurtz phát tri n t năm 1964 t i M , là ngôn ng dùng cho máy tính nh . Basicể ừ ạ ỹ ữ ỏ
d h c và s d ng không khó l m, song kh năng gi i quy t công vi c không l n. Đi uễ ọ ử ụ ắ ả ả ế ệ ớ ề
phi n toái n a là ngôn ng này thu c d ng "d tính" nên đ c phát tri n g n nh khôngề ữ ữ ộ ạ ễ ượ ể ầ ư
ki m soát đ c. T n t i quá nhi u "th ng " t Basic nên khó ch n th ti ng chu n m cể ượ ồ ạ ề ổ ữ ừ ọ ứ ế ẩ ự
cho ng d ng.ứ ụ
Năm 1975 Gates W. vi t ngôn ng cũng mang tên BASIC cho máy Altair, d ngế ữ ạ
microcomputer đ u tiên. Ngôn ng mang tên BASIC ngày nay th c t là các c i biên c aầ ữ ự ế ả ủ
th ti ng mà Gates đã đ a ra th i đó.ứ ế ư ờ
•Ngôn ng PLữ ( Programming Language ) còn đ c vi t d i d ng PL1 ho cượ ế ướ ạ ặ
PL/I, c i biên cách vi t PL1, đ c ng i kh ng l lúc b y gi IBM đ t ra trong th i gianả ế ượ ườ ổ ồ ấ ờ ặ ờ
1963 - 1966 sau thành công c a FORTRAN và các ngôn ng khác t i M . Ngôn ng th aủ ữ ạ ỹ ữ ừ
k nh ng k t qu t t đ p c a FORTRAN, Algol , Cobol . B n thân ngôn ng b c cao nàyế ữ ế ả ố ẹ ủ ả ữ ậ
cũng đã có tham v ng s d ng ngôn ng assembly làm các ph ng ti n n i ghép, ch yọ ử ụ ữ ươ ệ ố ạ
ch ng trình m u. Ng i ta đ t thêm s 1 cu i tên g i v i hàm ý "ngôn ng l p trình sươ ẫ ườ ặ ố ố ọ ớ ữ ậ ố
1". Tuy ý t ng hay, thi t k chu n song th c t không đ c nh ý mu n ch quan c aưở ế ế ẩ ự ế ượ ư ố ủ ủ
nh ng ng i sinh non ra nó. Ngôn ng đ c qu ng cáo rùm beng, song ng i dùng khôngữ ườ ữ ượ ả ườ
nhi u vì các compiler c a PL làm vi c quá t i. Ngôn ng không th đ c bao lâu, ngày nayề ủ ệ ồ ữ ọ ượ
th h tr kh i ph i nghe qu ng cáo ngôn ng number one n a .ế ệ ẻ ỏ ả ả ữ ữ
•Pascal ra đ i chính th c 1971. Ng i có công thi t k ngôn ng là Niklausờ ứ ườ ế ế ữ
Wirrth . Tên g i c a ngôn ng Pascal đ ghi nh công lao c a nhà toán h c l n th k 17ọ ủ ữ ể ớ ủ ọ ớ ế ỷ
Blaise Pascal. Ngôn ng Pascal thu c nhóm có c u trúc ch t, là ngôn ng l p trình tiêuữ ộ ấ ặ ữ ậ
chu n b t c ng i l p trình nào cũng nên bi t. Theo nh n đ nh c a các nhà chuyên môn,ẩ ấ ứ ườ ậ ế ậ ị ủ
đây là th ngôn ng "lingua franca", làm c ch c năng "common tongue", là ti ng nói chungứ ữ ả ứ ế
cho l p trình. Ngày nay trong các tr ng h c, trong các l p h c v l p trình, t i các kỳ thiậ ườ ọ ớ ọ ề ậ ạ
năng khi u ngôn ng này còn là ngôn ng chính th c đ truy n th và thi tài.ế ữ ữ ứ ể ề ụ
•C là ngôn ng l p trình đa năng, ng d ng vào vi c gi i quy t nh ng côngữ ậ ứ ụ ệ ả ế ữ
vi c th c t n y sinh t cu c s ng. C đ c coi là ngôn ng g n "ngôn ng máy", có khệ ự ế ả ừ ộ ố ượ ữ ầ ữ ả
năng gi i quy t m i công vi c mà nh ng ngôn ng l p trình "b c cao" sinh tr c nó nhả ế ọ ệ ữ ữ ậ ậ ướ ư
FORTRAN, PL1, Pascal đã làm, đ ng th i còn gi i quy t c nh ng vi c mà đàn anh khôngồ ờ ả ế ả ữ ệ
mu n ch m t i, nh ng vi c ch giành cho ngôn ng g n gũi máy nh Assembler gi iố ạ ớ ữ ệ ỉ ữ ầ ư ả
quy t.ế
L ch s phát tri n c a C có nhi u đi u đáng nh c. Yêu c u th c t c a AT & T làị ử ể ủ ề ề ắ ầ ự ế ủ
ph i có ngôn ng dùng cho h đi u hành UNIX, s d ng trên máy DEC PDP - 11. Vi cả ữ ệ ề ử ụ ệ
này đ c giao cho Nennis Ritchie. H đi u hành, compiler và ch ng trình ng d ng đ uượ ệ ề ươ ứ ụ ề
đ c D.Ritchie vi t b ng C năm 1972. Th c ra, tr c đó Martin Richards đã đ c giaoượ ế ằ ự ướ ượ
công vi c t ng t và k t qu c a nó là ra đ i ngôn ng có tên vi t t t BCPL. Trên c sệ ươ ự ế ả ủ ờ ữ ế ắ ơ ở
BCPL năm 1970 Ken Thompson so n ngôn ng B (có th b t ngu n t cái tên BCPL) và đãạ ữ ể ắ ồ ừ
so n đ ph n m m đ đi u hành DEC PDP - 7. Vào năm 1972 v i s c ng tác c aạ ủ ầ ề ể ề ớ ự ộ ủ
K.Thompson , D.Ritchie đã đi t B đ n C. Ngu n g c c a tên g i "C" ch đ n gi n v y.ừ ế ồ ố ủ ọ ỉ ơ ả ậ
Năm 1978 nhà xu t b n Prentice - Hall tung ra th tr ng "The C Pragramming Language"ấ ả ị ườ
5