
TỔNGHỢPHỆTHỐNGĐIỀUKHIỂNCHOQUADROTOR
PhùngĐìnhKiên
Email:kiensuong9614@gmail.com
Ngàytòasoạnnhậnđượcbàibáo:07/05/2024
Ngàyphảnbiệnđánhgiá:14/11/2024
Ngàybàibáođượcduyệtđăng:28/11/2024
DOI:10.59266/houjs.2024.485
Tómtắt:Quadrotorđượcứngdụngnhiềutronggiámsátnúilửa,cháyrừng,kiểmtra
đườngdâyđiện,tìmkiếmngườithấtlạc,cứuhộthiêntai,....Quadrotorđượctrangbịbốn
độngcơvới4cánhquạtvớimụcđíchđiềukhiểnvàổnđịnhchuyểnđộngcủaquadrotor,điều
nàylàmchomôhìnhđộnglựchọccủaquadrotorphứctạpvàcósựphituyếnmạnh.
Bàibáo
tậptrungpháttriểnmôhìnhtoánquadrotor,thiếtkếbộđiềukhiểnPIDYjLQR,tiếnhànhmô
hìnhhóavàmôphỏngcácbộđiềukhiểntrênMatlab/Simulink.Cáckếtquảmôphỏngđược
đưarađểchứngminhtínhhiệuquảcủacácbộđiềukhiển.
Từkhóa:Tổnghợphệthốngđiềukhiển,Quadrotor,UAV,LQR,PID.
KhoaVôtuyếnđiệntử,TrườngSĩquanKhôngquân
I.Đặtvấnđề
Hiện nay,trên thế giới, thiết bị bay
khôngngườilái(haycòngọilà-UAV)ngày
càngpháttriểnvàđượcứngdụngrộngrãi
trongcảlĩnhvựcquânsựvàdânsự.Trong
đó,loạiQuadrotorđangđượcsửdụngphổ
thônghơnnhờvàocấutrúcđơngiản,tính
đốixứng,dễdàngthiếtkế,điềukhiểnvàcó
thểhoạtđộnglinhhoạttrongkhuvựcnhỏ.
Tuy nhiên, việc xây dựng một hệ thống
UAVhoànchỉnhkhôngđơngiảnvàtồntại
rấtnhiềurủironhưsaisốvềthiếtkếcácchi
tiếtphầncứng,thuậttoánhoạtđộngkhông
ổnđịnh,trongquátrìnhhoạtđộngcóthểgây
ranhữngtainạnngoàiýmuốnv.v.Việcthiết
kếmộtbộđiềukhiểnchothiếtbịlàmộtvấn
đềquantrọnghàngđầu.
Trongthựctếcórấtnhiềunghiêncứu
vềbộđiềukhiểnchoquadrotorcủanhiềutác
giảđưara.Trongbàibáonàytácgiảđisâu
tổnghợp2bộđiềukhiểnlà:bộđiềukhiển
PID và bộ điều khiểntốiưu toànphương
tuyếntínhLQR. Kếtquả được môphỏng
trên phần mềm Matlab/Simulink với các
thôngsốcủaquadrotorbấtkỳ,quađórútra
ưunhượcđiểmcủatừngbộđiềukhiển.
II.Cơsởlýthuyết
2.1. Biến đổi mô hình toán của
quadrotor
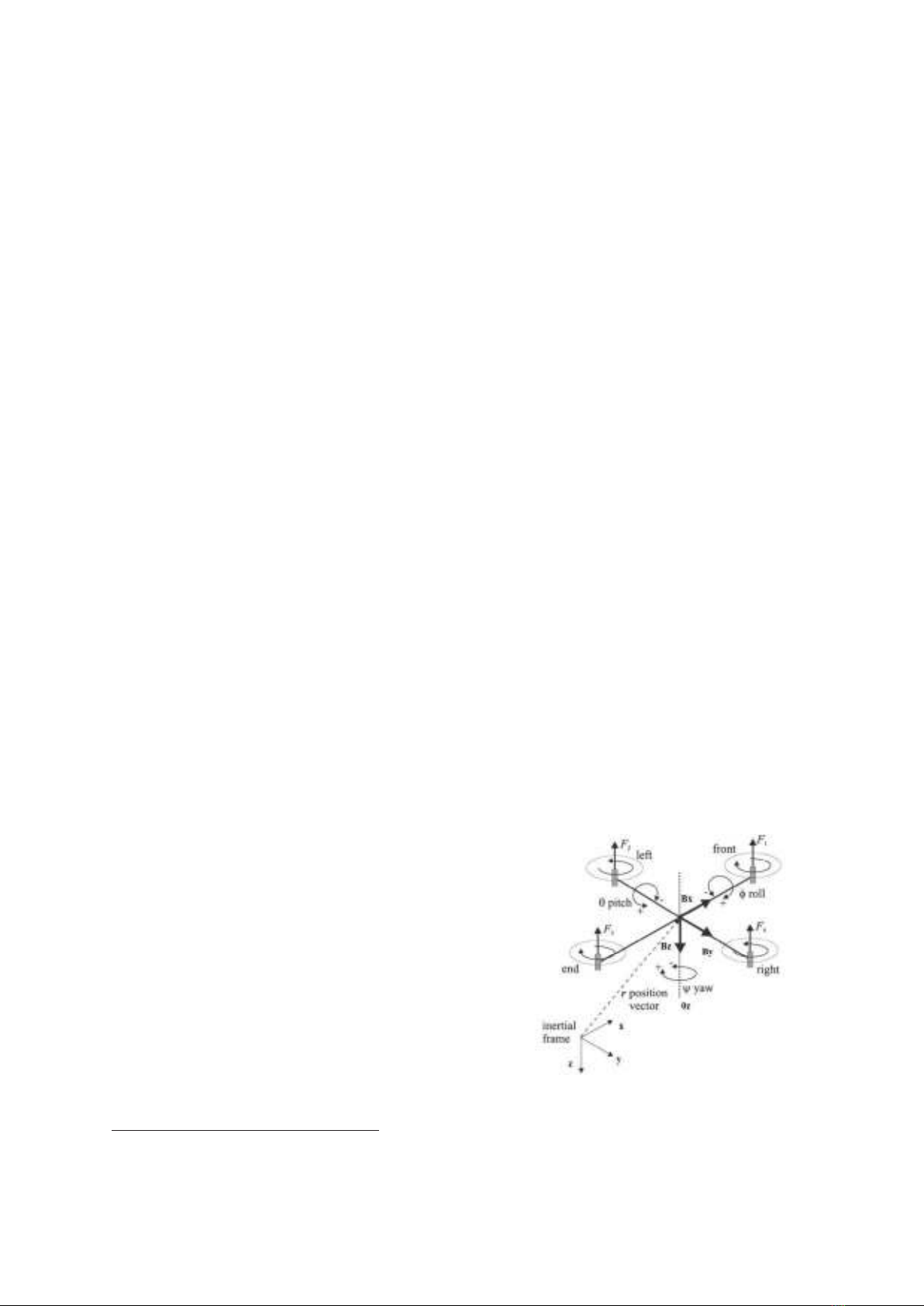
Hình1.HệtọađộđốivớiQuadrotor

Môhìnhtoáncủaquadrotordạngphituyến:[2][6]
(1)
Nhiệmvụcủabộđiềukhiểnlàđiều
chỉnh tọa độ vị trí
(x , y ,z )
và trạng
thái
( , , )Φ θ Ψ
ban đầu của quadrotor
vềtọađộvịtrí
d d d
(x , y , z )
vàtrạngthái
d d d
( , , )Φ θ Ψ
mongmuốn.Nhưvậy,việc
ổn định quỹ đạo của quadrotor sẽ được
thựchiệnthôngqua6kênhđiềukhiểnđó
là:kênhxdọctrụcox,kênhydọctrụcoy,
kênhđộcaozdọctrụcoz,kênh
Φ
,kênh
θ
vàkênhΨ.
Gọivectơ trạngtháicủaquadrotor
là
X
r
,
X
r
chứa 12 thành phần động học
của quadrotor theo thứ tự như sau:
X X( , , , , , ,z, z,x,x, y, y)= Φ Φ θ θ Ψ Ψ
&&
&& & &
Để thực hiện điều khiển, ta phân
chia trạng thái của quadrotor theo từng
kênhđiềukhiểntươngứng.Căncứvàohệ
phương trình (1) và vectơ trạng thái ta
thànhlậpcácphươngtrìnhđộnghọctương
ứngvớitừngkênhđiềukhiểnnhưsau.
Đốivớikênhđiềukhiểngócnghiêng
Φ,tacóhệphươngtrìnhđộnghọctương
ứngnhưsau:
(2)
Đặt
X= Φ
và
X= Φ
&
, do đó
X= Φ
&&
và
X= Φ
&&&
.Đặt
x 2
T U=
Từđó
suy ra mô hình dạng truyền ngược chặt
theokênhΦlà:
(3)
Đối vớikênh điều khiển góc chúc
ngócθ,tacũngcóhệphươngtrìnhđộng
họctươngứng:
(4)
Đặt
X= θ
và
X= θ
&
,dođó
X= θ
&
&
và
X= θ
&&
&
.Đặt
y 3
T U=
Từđósuyramô
hìnhdạngtruyềnngượcchặttheokênhθlà:
(5)
Đối vớikênh điều khiển góc chúc
hướngΨ,tacũngcóhệphươngtrìnhđộng
họctươngứng:
(6)
Đặt
X= Ψ
và
X= Ψ
&
, do đó
X= Ψ
& &
và
X= Ψ
& &&
.Đặt
z
T U=
Từđó
suy ra mô hình dạng truyền ngược chặt
theokênhΨ:
(7)

Đối với kênh z, ta có hệ phương
trìnhđộnghọc:
(8)
Đặt
X z=
và
X z=
&
,dođó
X z=
&&
và
X z=
&&&
.Đặt
L 1
F U=
.Từđósuyramô
hìnhdạngtruyềnngượcchặttheokênhzlà:
(9)
Đốivớikênhx,tacóhệphươngtrình
độnghọc:
(10)
Đặt
X x=
và

X x=
&, do đó
X z=
&&
và

X x=
&&&
.Từđósuyramôhình
dạngtruyềnngượcchặttheokênhxlà:
(11)
Trongđó
d d d
, ,Φ θ Ψ
làcácgócEuler
mongmuốn.
Đối với kênh y, ta có hệ phương
trìnhđộnghọc:
(12)
Đặt

X y=
và

X y=
&, do đó

X y=
&&
và

X y=
&&&
.Từđósuyramôhình
dạngtruyềnngượcchặttheokênhylà:
(13)
Đặt
yy zz
xx
J J
aJ
−
=
,
zz xx
yy
J J
aJ
−
=
,
xx yy
zz
J J
aJ
−
=,
xx
L
bJ
=
,
yy
L
bJ
=
,
zz
L
bJ
=
.
t 1 3
U cos(X )cos(X )=
.
x 1 3 5 1 5
U cos(X )sin(X )cos(X ) sin (X )sin(X )= +
y 1 3 5 1 5
U cos(X )sin(X )sin (X ) sin (X )cos(X )= −
Khiđó,phươngtrìnhtrạngtháiphituyếncódạng:
t 1

 x 1


X
X X a b U
f (X,U)
X
f (X,U)
X X a b U
f (X, U)
X
f (X,U)
X X a b U
f (X,U)
X
f (X, U)
X f (X, U)
f (X,U) g u ( )U
m
f (X, U) X
f (X,U)
f (X,U) u ( )U
m
f (X, U) X
f (X,U)
+
+
+
= = =
− +
&

y 1
u ( )U
m

(14)

Ápdụngphươngpháptuyếntínhhóa,theo[7],saukhithựchiệntuyếntínhhóa,tanhận
đượcmôhìnhkhônggiantrạngtháituyếntínhnhưsau:



X
X
X
X
X
X
X
X
X
X
X
X
=
&
&
&
&
&
&
&
&
&
&
&
&



X0 b 0 0
X
X0 0 b 0
X
X0 0 0 b
X
X
X( ) 0 0 0
m
X
X
X
X
+
−
U
U
U
U

(15)



X
X
X
X
Y X U
Y X U 
Y X U
 
Y X U 
X
X
X
X
= +

(16)
Hình2.GiaodiệnGUIchươngtrìnhTổnghợphệthốngđiềukhiểnchoQuadrotor
Nhưvậy,biếnđổimôhìnhtoánhọc
củaquadrotorthànhcáchệtruyềnngược
chặttheosáukênhđiềukhiển(x,y,z,Φ,θ,Ψ)
và tuyếntínhhóa, tasẽđưavề môhình
khônggiantrạngthái.Đâylàcơsởtrong
việctổnghợpbộđiềukhiểnPIDvàLQR.
Ứng với mỗi loại Quadrotor khác
nhausẽcóthôngsốhệthốngkhácnhau,
dođómôhìnhkhônggiantrạngtháicũng
đượcxácđịnhbởicácmatrậnđặctrưng
riêng. Với việc lập trình trên GUI của
MatLab,đầuvàolànhậpcácthôngsốhệ
thống của Quadrotor gồm: J
x
(Moment
quán tínhtheotrục x),J
y
(Momentquán
tính theo trục y), J
z
(Moment quán tính
theotrụcz),J
r
(Momentquántínhrotor),
M (khối lượng quadrotor), L (Khoảng
cáchtừtrọngtâmquadrotorđếntrụcđộng
cơ),b(lựcđẩy),d(lựckéo).Chươngtrình
sẽtựđộngtínhtoánvàxácđịnhphương
trìnhkhônggiantrạngtháiđặctrưngcho
môhìnhQuadrotor(hình2).

2.2.
XâydựngbộđiềukhiểnPID
choquadrotor
Trongphầnnày,tácgiảtổnghợpbộ
điềukhiển PID với mục đích khảo sátvà
đánhgiáchấtlượngđiềukhiểntrongchếđộ
ổnđịnhquỹđạochoquadrotor.Tổnghợpbộ
điềukhiểnthựchiệntheokênhđộcao.
Xétchếđộổnđịnhđộcao,trongđó
tínhiệuđầuvàokênhzlàz
d
códạnghàm
bậc thang đơn vị, còn tín hiệu đầu vào
kênhxvàytươngứnglàx
d
=0vày
d
=
0nhằmgiảmbớthiệntượngxenkênhdo
cáckênhđiềukhiểnảnhhưởnglẫnnhau.
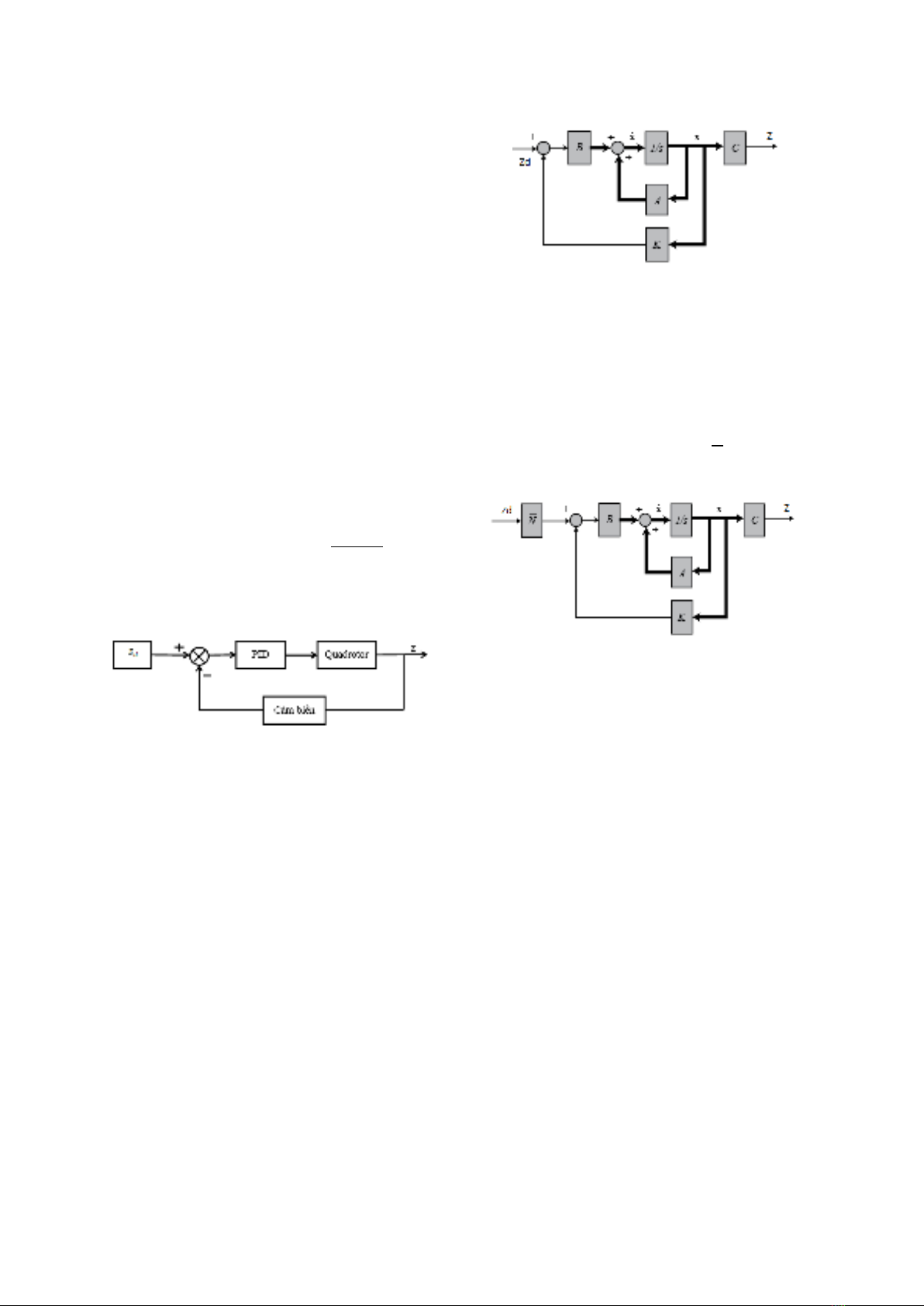
Luậtđiềukhiểnchokênhđộcaocó
dạngnhưsau:
d
1 p d i d d
d(z z)
U K .(z z) K (z z)dt K
dt
−
= − + − +
∫
(17)
Sơđồđiềukhiểntheokênhđộcao
đượcmôtảtronghình3.
Hình3.Sơđồđiềukhiểnkênhđộcao
2.3.
Xâydựngbộđiềukhiểntối
ưu toàn phương tuyến tính (LQR)
choquadrotor
Lý thuyết điều khiển điều khiển
LQR là một phương pháp điều khiển
mạnh để điềukhiểnhệ thống tuyếntính
đượcmôtảbằngphươngtrìnhtrạngthái.
KỹthuậtLQRtạorabộđiềukhiểnvòng
kínổnđịnhvớinănglượngcungcấpcho
hệthốnglànhỏnhất.
Hình4làmôhìnhđểđiềukhiểnvịtrí
củaquadrotortheokênhđộcaođượcxây
dựngbằngcáchchọnmatrậntrạngtháiA
vàBtừdạngkhônggiantrạngtháicủamô
hìnhvịtrí;vàmatrậnđộlợiKđượctính
từcácmatrậntrọnglượngQvàR.
Hình4.Môhìnhđiềukhiểnvịtrícủa
quadrotortheokênhđộcao
Thôngthường,đốivớihệthốngsử
dụngbộđiềukhiểnLQRsẽtồntạisaisố
xáclập,dovậytacầnthiếtkếthêmkhâu
bù,khâubùthựcchấtlàđưathêmlượng
điềukhiểntíchphânđầurađểđưasaisố
xáclậpvềkhông.Khâubù
N
đượcxác
địnhbởihệsốKbu.
Hình5.Môhìnhđiềukhiểnvịtrícủa
quadrotortheokênhđộcaokhiđưathêm
khâubù
III.Phươngphápnghiêncứu
Quátrìnhnghiêncứuđượctácgiảtiến
hànhtheophươngphápnghiêncứucơsởlý
thuyếtgắnvớimôphỏngđánhgiácácbộ
điềukhiểntrênphầnmềmmatlab/simulink.
3.1.Nghiêncứulýthuyết
-Nghiêncứulýthuyếtmôhìnhtoán
củaquadrotorvàcáchbiếnđổiđưavềdạng
môhìnhkhônggiantrạngtháituyếntính.
- Nghiên cứu lý thuyết cách xây
dựngcácbộđiềukhiểnPID,LQR.
- Ứng dụnglýthuyếtxâydựngbộ
điều khiển PID và LQR cho quadrotor
theokênhđộcao.
3.2.Nghiêncứuthựcnghiệm
-Kiểmchứngkếtquảxâydựngbộ
điềukhiểnPIDvàLQRchoquadrotortrên
phầnmềmmatlab/simulink.Từđó,rútra