TUYỂN T Ậ P CÁCBÀI HÌNH GIẢI TÍCH PHẲNG O X Y TRONG
ĐỀ THI THỬ ĐẠI HỌC
PHẦN THỨ NHẤT : NĂM 2013 - 2014
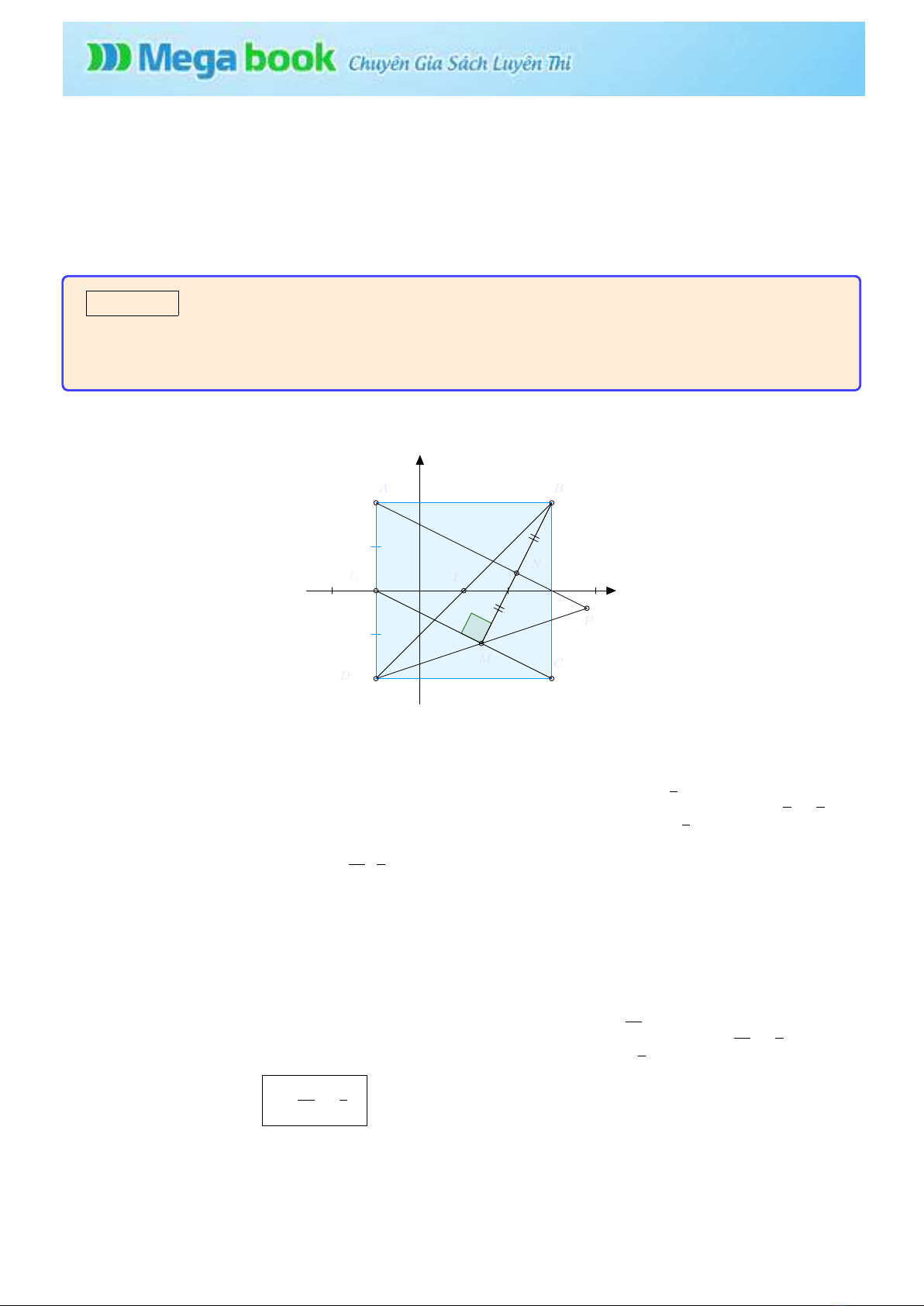
Bài toán 1: T r o n g mặt phẳng v ớ i hệ tọa độ vuông góc Oxy,c h o hình vuông ABCD có các đỉnh
A(−1; 2) ; C(3; −2). Gọi Elà trung điểm cạnh AD ;BMlà đường thẳng vuông góc v ớ i CEtại M
;Nlà trung điểm cạnh BMv à Plà giao điểm của AN v à DM. Biết phương trình đường thẳng
BM:2x−y−4 = 0 .Tìm tọa độ đỉnh P.
L ờ i giải:
A B
C
D
E
M
N
P
I
- Phương trình ECđi qua Cvuông góc v ớ i BMlà: x+2y+ 1 = 0
-T ọ a độ điểm M=EC∩BMlà nghiệm của hệ n2x−y−4 = 0
x+2y+ 1 = 0 ⇐ ⇒
x=7
5
y=−6
5
= ⇒M7
5
;−6
5
- Do Nlà trung điểm BMsuy ra N11
5;2
5
- Phương trình AN qua hai điểm Av à Nlà x+2y−3 = 0
- Gọi Ilà tâm hình vuông suy ra I(1; 0). Phương trình BDqua Ivuông góc v ớ i AC là x−y−1 = 0
-T ọ a độ Blà nghiệm của hệ n2x−y−4 = 0
x−y−1 = 0 ⇐ ⇒ nx= 3
y= 2 = ⇒B(3; 2)
- Do Ilà trung điểm BDsuy ra tọa độ D(−1; −2)
- Phương trình DM qua Dv à Mlà x−3y−5 = 0
-T ọ a độ P=DM∩AN là nghiệm của hệ nx−3y−5 = 0
x+2y−3 = 0 ⇐ ⇒
x=19
5
y=−2
5
= ⇒P19
5;−2
5
Kết luận: T ọ a độ điểm P19
5;−2
5thỏa mãn y ê u cầu bài toán.
1
http://megabook.vn
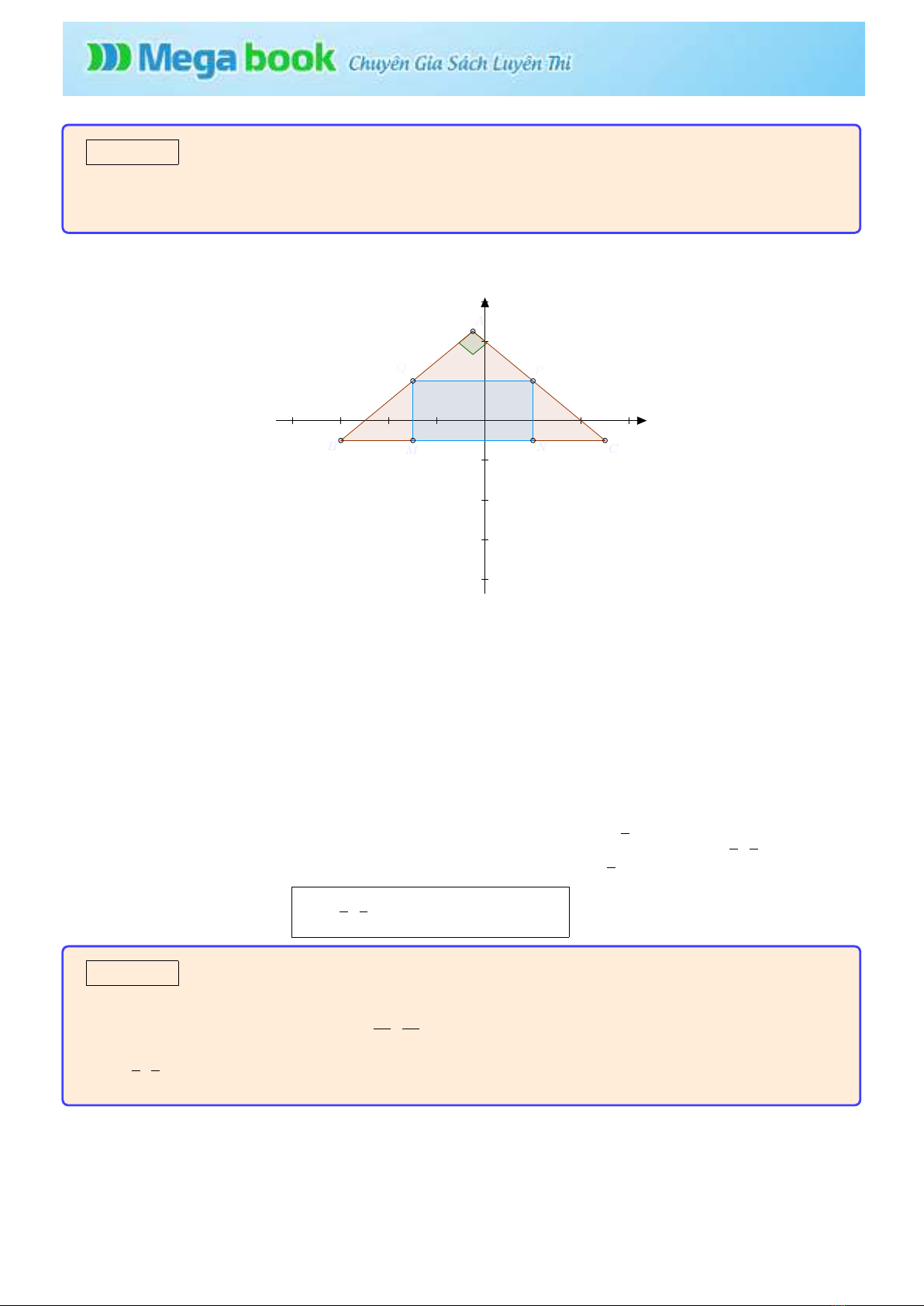
Bài toán 2: T r o n g mặt phẳng v ớ i hệ tọa độ vuông góc Oxy, tam giác ABC vuông tại Angoại tiếp
hình c h ữ nhật MNPQ. Biết các điểm M(−3; −1) v à N(2; −1) thuộc cạnh BC;Qthuộc cạnh AB v à
Pthuộc cạnh AC. Đường thẳng AB có phương trình x−y+ 5 = 0. Tìm tọa độ các đỉnh của tam giác
ABC
L ờ i giải:
A
C
BMN
P
Q
- Phương trình đường thẳng BCqua Mv à Nlà y+ 1 = 0
-T ọ a độ điểm B=AB ∩BClà nghiệm của hệ nx−y+ 5 = 0
y+ 1 = 0 ⇐ ⇒ nx=−6
y=−1= ⇒B(−6; −1)
- Đường thẳng QM qua Mvuông góc v ớ i BCcó phương trình là x+ 3 = 0
-T ọ a độ Q=QM ∩AB là nghiệm của hệ nx+ 3 = 0
x−y+ 5 = 0 ⇐ ⇒ nx=−3
y= 2 = ⇒Q(−3; 2)
-T a có − − → MN= (5; 0) ; − − − → QP =(xP+ 3; yP−2) = ⇒− − → MN=− − − → QP ⇐ ⇒ nxP= 2
yP= 2 = ⇒P(2; 2)
- Đường thẳng AC qua Pvuông góc v ớ i AB là x+y−4 = 0
-T ọ a độ C=AC ∩BClà nghiệm của hệ nx+y−4 = 0
y+ 1 = 0 ⇐ ⇒ nx= 5
y=−1= ⇒C(5; −1)
-T ọ a độ A=AB ∩AC là nghiệm của hệ nx+y−4 = 0
x−y+ 5 = 0 ⇐ ⇒
x=−1
2
y=9
2
= ⇒A−1
2
;
9
2
Kết luận: T ọ a độ các điểm A−1
2
;
9
2;B(−6; −1) ; C(5; −1) .
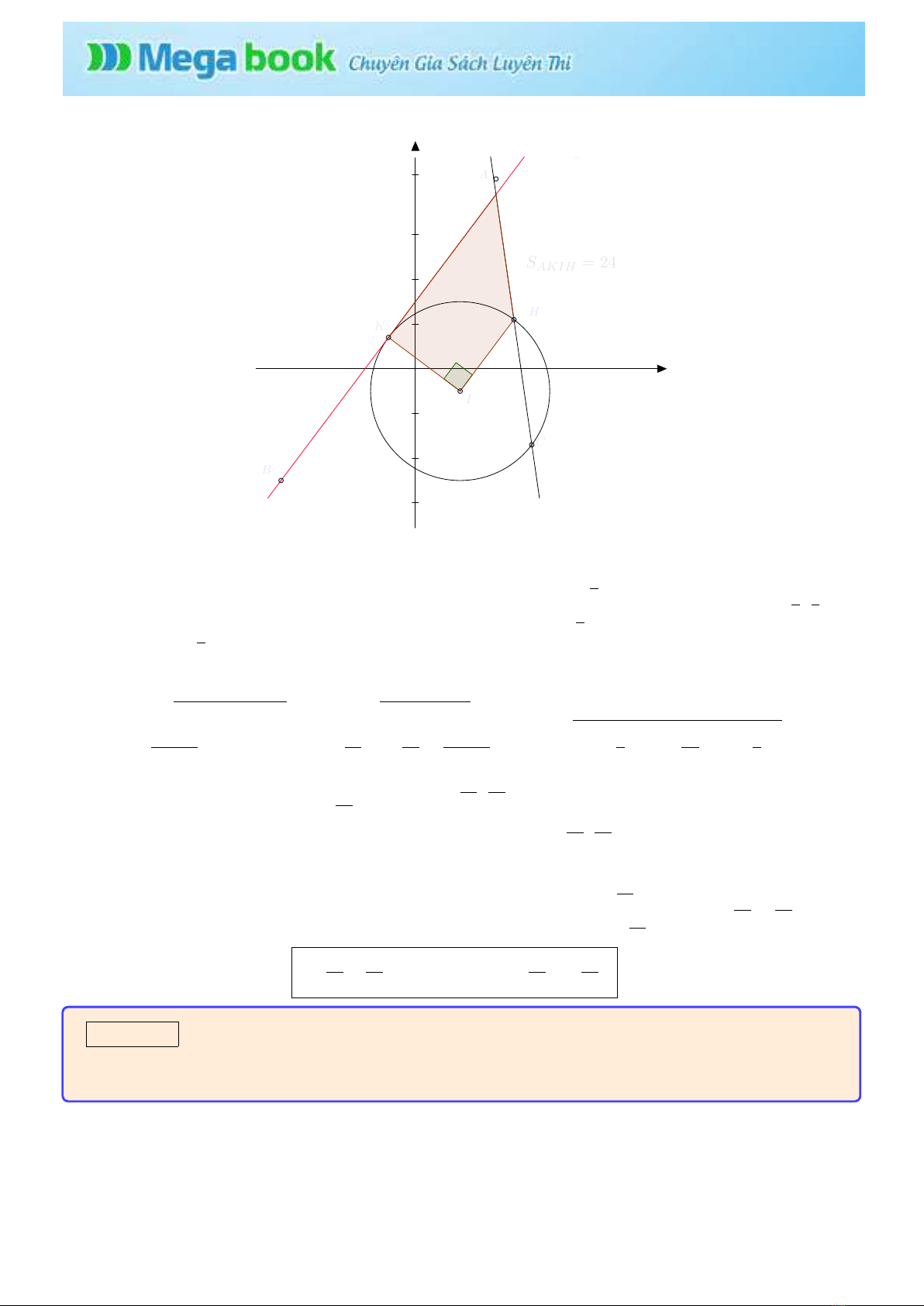
Bài toán 3: T r o n g mặt phẳng v ớ i hệ tọa độ vuông góc Oxy,cho đường tròn (C) : x2+y
2−4x+
2y−11 = 0 v à đường thẳng (d) : 4x−3y+ 9 = 0. Gọi A;Blần lượt là hai điểm thuộc (d)v à Clà điểm
thuộc đường tròn (C). Biết điểm H22
5;11
5là một giao điểm của AC v à (C)(C6 =H)v à điểm
K−6
5
;
7
5là trung điểm của AB. Tìm tọa độ các đỉnh A;B;C.
L ờ i giải:
2http://megabook.vn
SAKIH= 24
A
d:4x−3y=−9
K
B
H
I
C
- Đường tròn (C)có tâm I(2; −1); bán kính R=4.
-T ọ a độ (d)∩(C)thỏa x2+y
2−4x+2y−11 = 0
4x−3y+ 9 = 0 ⇐ ⇒
x=−6
5
y=7
5
= ⇒(d)∩(C) = K−6
5
;
7
5
-T a có HK=4√2= ⇒HK
2=IH
2+IK
2=R2+R2= ⇒∆IHKvuông tại Isuy ra tứ giác AHIK là
hình thang vuông tại Iv à K.
= ⇒SAHIK=(AH +IK)IH
2= 24 ⇐ ⇒ (AH +R)R
2= 24 = ⇒AH = 8
- Gọi Aa;3a+ 9
3∈(d)= ⇒B−12
5−a;14
5−3a+ 9
3.Ta có sa+6
52
+4a
3+ 3 −7
52
= 8
⇐ ⇒ 5a2
+12a−180 = 0 ⇐ ⇒ "a=18
5
a=−6= ⇒
A18
5;39
5→B(−6; −5)
A(−6; −5) →B18
5;39
5(Loại do A;Bkhác phía v ớ i IK)
- Phương trình AC qua Av à Hlà 7x+y−33 = 0
-T ọ a độ C=(C)∩AC thỏa x2+y
2−4x+2y−11 = 0
7x+y−33 = 0 ⇐ ⇒
x=26
5
y=−17
5
= ⇒C26
5;−17
5
Kết luận: T ọ a độ các điểm A18
5;39
5;B(−6; −5) ; C26
5;−17
5.
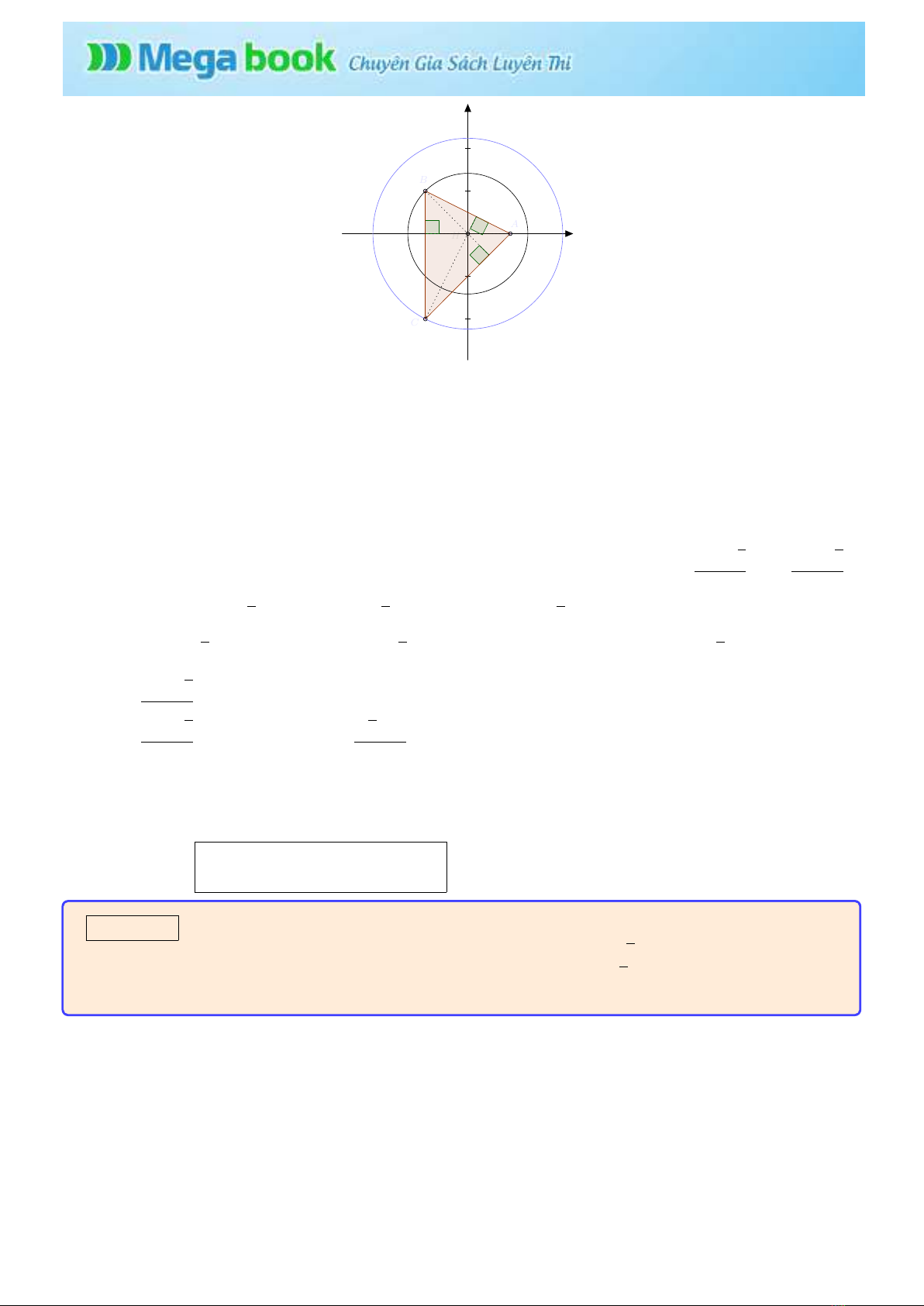
Bài toán 4: T r o n g mặt phẳng v ớ i hệ tọa độ vuông góc Oxy c h o điểm A(1; 0) v à các đường tròn
(C1
) : x2+y
2= 2; (C2
) : x2+y
2= 5 . Tìm tọa độ các điểm Bv à Clần lượt nằm trên (C1
)v à (C2
)
để tam giác ABC có diện tích lớn nhất.
L ờ i giải:
3
http://megabook.vn
A
B
C
H
* Đầu tiên ta có nhận xét: để tam giác ABC có diện tích lớn nhất thì Ophải là trực tâm của tam giác ABC.
Chứng minh:
Giả sử COkhông ⊥AB thì ta luôn tìm được điểm C
′∈(C2
)sao c h o d(C
′
, AB)lớn hơn d(C,AB), hay
S∆ABC
′lớn hơn S∆ABC→không thỏa mãn y ê u cầu bài toán. Do đó CO⊥AB
-Tương tự ta cũng có BO⊥AC
V ậ y Olà trực tâm của tam giác ABC.Suy ra AO ⊥BC ⇐ ⇒ xB=xC
V à ta giả sử B(t;b)∈(C1
),C(t;c)∈(C2
)(t, b, c ∈R) thì ta có t2+b2= 2
t2+c2= 5 ⇐ ⇒ b2= 2 −t2
c2= 5 −t2
Mà CO⊥AB nên − − − → CO.
− − − → AB = 0 hay t(t−1) + bc = 0 suy ra b2
c2=t4−2t3+t2
Do đó (2 −t2
)(5 −t2
) = t4−2t3+t2⇐ ⇒ (t+ 1)(2t2−10t+ 10) ⇐ ⇒ t=−1; t=5 + √5
2;t=5−√5
2
T ớ i đây ta có: S∆ABC=1
2
BC.d(A, BC) = 1
2
|xA−xB
||yB−yC
|=1
2
|1−t||b−c|
Suy ra S
2
∆ABC=1
4
(1 −t)2
(b2+c2−2bc) = 1
4
(1 −t)2
((2 −t2
) + (5 −t2
)−2(t−t2
)) = 1
4
(1 −t)2
(7 −2t)
* Nếu t=−1thì ta suy ra S
2
∆ABC= 9 hay S∆ABC= 3
* Nếu t=5 + √5
2thì ta dễ thấy điều v ô lí vì t2+b2=2.
* Nếu t=5−√5
2thì ta có S
2
∆ABC=√5−1
8<9→Loại.
Suy ra v ớ i t=−1thì S∆ABClớn nhất.
V à ta có
bc =−2
b2= 1
c2= 4 ⇐ ⇒ b= 1
c=−2∨b=−1
c= 2 = ⇒B(−1; 1)
C(−1; −2) ∨B(−1; −2)
C(−1; 2)
Kết luận: V ớ i B(−1; 1)
C(−1; −2) ∨B(−1; −2)
C(−1; 2) thì tam giác ABC có diện tích lớn nhất
Bài toán 5: T r o n g mặt phẳng v ớ i hệ tọa độ vuông góc Oxyc h o hình thoi ABCD có b
A= 600
.Trên
các cạnh AB, BClấy các điểm M,Nsao c h o MB+NB=AB.Biết P(√3; 1) thuộc đường thẳng DN
v à đường phân giác trong của góc \
MDNcó phương trình là d:x−y
√3 + 6 = 0.Tìm toạ độ đỉnh D
của hình thoi ABCD.
L ờ i giải:
Từ giả thiết b
A= 600= ⇒tam giác ABD, CBDlà các tam giác đều.Theo đề bài ta có AM =BN,BM=CN.
Xét hai tam giác ADM v à BDNta có: \
DAM =\
DBN = 600
,AD =BD,AM =BN ⇐ ⇒ hai tam giác
bằng nhau ⇐ ⇒ \
ADM =\
BDN(1).
Xét hai tam giác BMDv à CNDta có: \
DBM =\
DCN = 600
,CD=BD,CN=BM ⇐ ⇒ hai tam giác
bằng nhau ⇐ ⇒ \
NDC=\
MDB(2).
Từ (1) v à (2) ⇐ ⇒ \
MDN= 600
.
Gọi P′là điểm đối xứng của Pqua đường phân giác d= ⇒P′thuộc đường thẳng DM
= ⇒tam giác PDP
′là tam giác đều. = ⇒DP =P P ′=2d(P/d)=6.
4http://megabook.vn
Gọi Dcó tọa độ Da;a+ 6
√3.T a có: PD
2=(a−√3)2+
a+ 6 −√3
√3!2
= 36
⇐ ⇒ a= 3 + √3∨a=−6 + √3⇐ ⇒ D(3 + √3; 1 + 3√3) ∨D(−6 + √3; 1).
Kết luận: T ọ a độ D(3 + √3; 1 + 3√3) ∨D(−6 + √3; 1) thỏa mãn bài toán.
Bài toán 6: T r o n g mặt phẳng v ớ i hệ tọa độ vuông góc Oxy,c h o hình c h ữ nhật ABCD , đỉnh B
thuộc đường thẳng d1: 2x−y+ 2 = 0, đỉnh Cthuộc đường thẳng d2:x−y−5 = 0 .Gọi Hlà hình
c h i ế u của Bxuống đường c h é o AC . BiếtM9
5
;
2
5;K(9; 2) lần lượt là trung điểm của AH v à CD.
Tìm toạ độ các đỉnh của hình c h ữ nhật ABCD biết hoành độ đỉnh Clớn hơn 4.
L ờ i giải:
A
BC
D
HK
M
Gọi B(b;2b+ 2),C(c;c−5),(c > 4) v à Elà điểm đối xứng v ớ i Bqua C. Suy ra E(2c−b;2c−2b−12).
Dễ dàng c h ứ n g minh được Klà trung điểm của AE. Do đó,
−−− →
HE=2− − → MK=72
5;16
5= ⇒H2c−b−72
5;2c−2b−76
5.
Thiết lập tọa độ các v e c t o r
−−− →
CK= (9 −c; 7 + c),− − − → BC=(c−b;c−2b−7),
− − − → BH=2c−2b−72
5;2c−4b−86
5,− − → MC=c−9
5
;c−27
5.
V ớ i giả thiết bài toán ta có hệ phương trình
(−−− →
CK.
− − − → BC= 0
−−− →
BH.
− − → MC= 0 ⇐ ⇒ (−2c2+3bc + 23c−23b−49 = 0
4c2−6bc +126
5b−46c+594
5= 0 ⇐ ⇒ b= 1
c= 9 hoặc c= 4(loại)
Từ đó ta có B(1; 4),C(9; 4) .Vì Klà trung điểm của CDnên suy ra D(9; 0) .Lại có Clà trung điểm của
BEnên suy ra E(17; 4),v à Klà trung điểm của AE nên suy ra A(1; 0) .
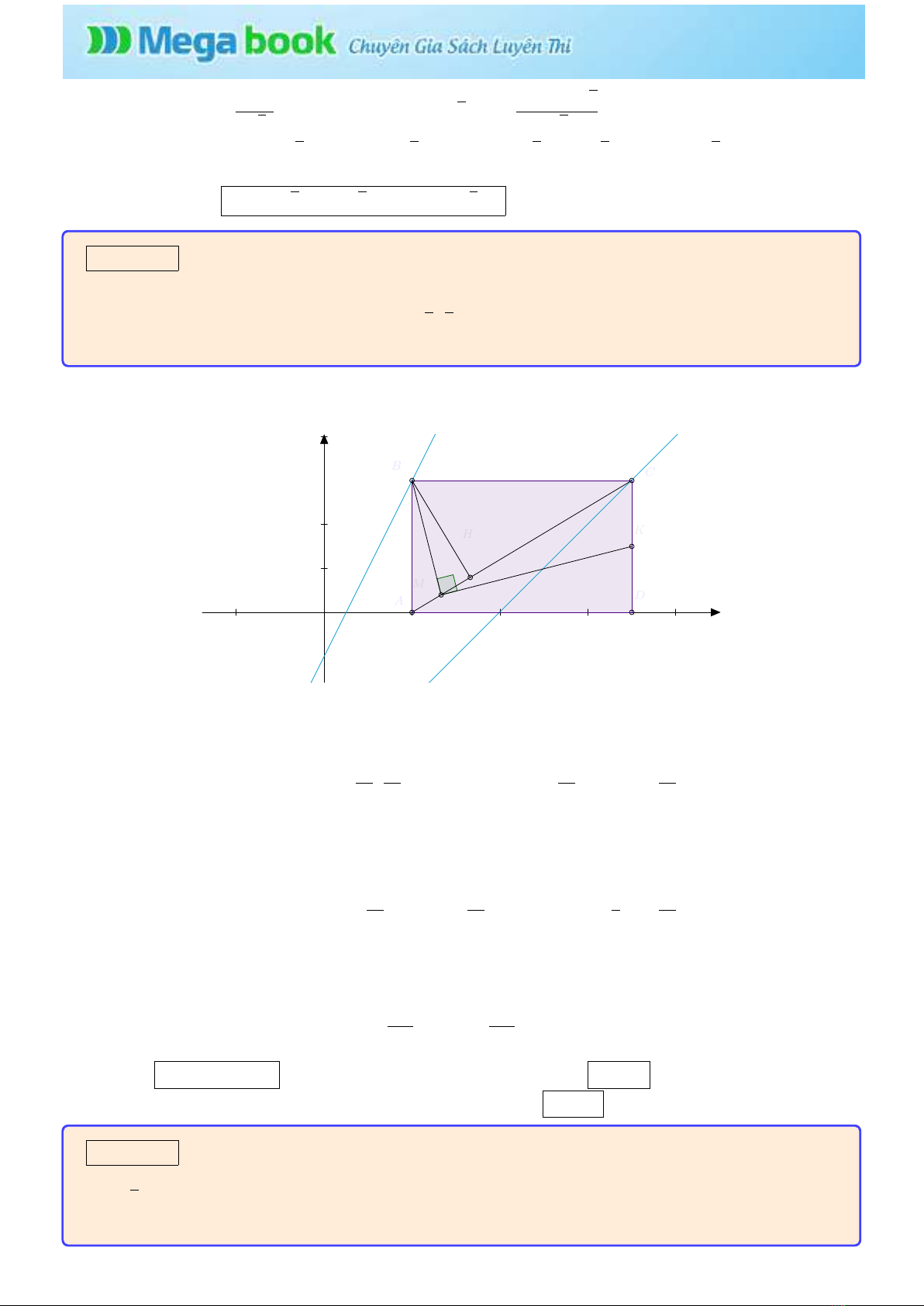
Bài toán 7: T r o n g mặt phẳng v ớ i hệ trục tọa độ Đề-các vuông góc Oxy, c h o đường tròn (C) :
x−5
42
+(y−1)2= 2 .Xác định tọa độ các đỉnh của hình vuông ABCD biết các đỉnh Bv à C
thuộc đường tròn (C), các đỉnh Av à Dthuộc trục Ox.
5
http://megabook.vn