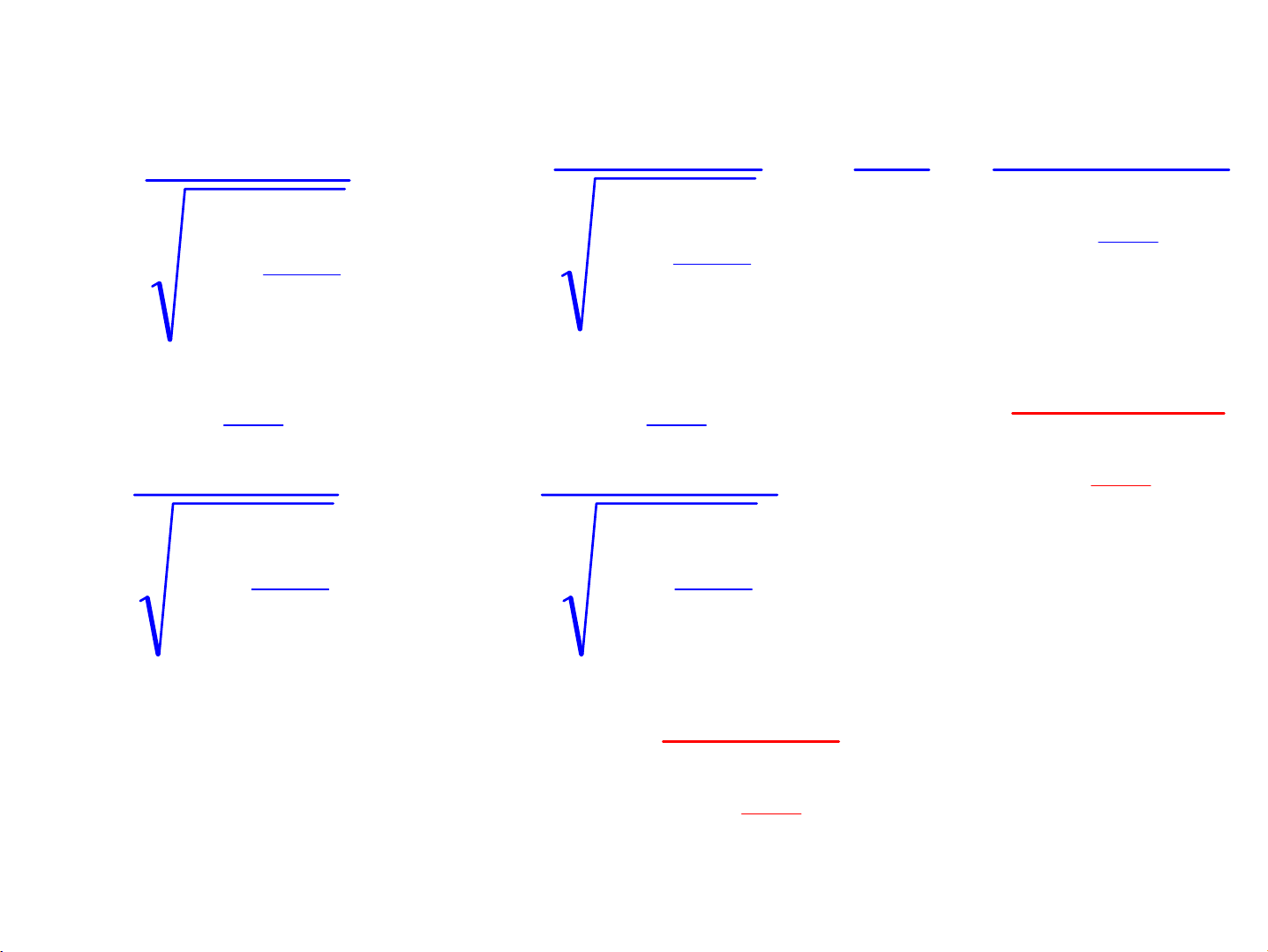
2
2
c
V
1
Vtx
'x
−
−
=
2
2
2
c
V
1
x
c
V
t
't
−
−
=
2
2
c
V
1
Vdtdx
'dx
−
−
=
2
2
2
c
V
1
dx
c
V
dt
'dt
−
−
=
dx
c
V
dt
Vdtdx
'dt
'dx
2
−
−
=
x
2
x
x
u
c
V
1
Vu
'u
−
−
=
4.3. §Þnh lý vÒ tæng hîp vËn tèc
NÕu ux=c th× c
c
c
V
1
Vc
'u
2
x=
−
−
=
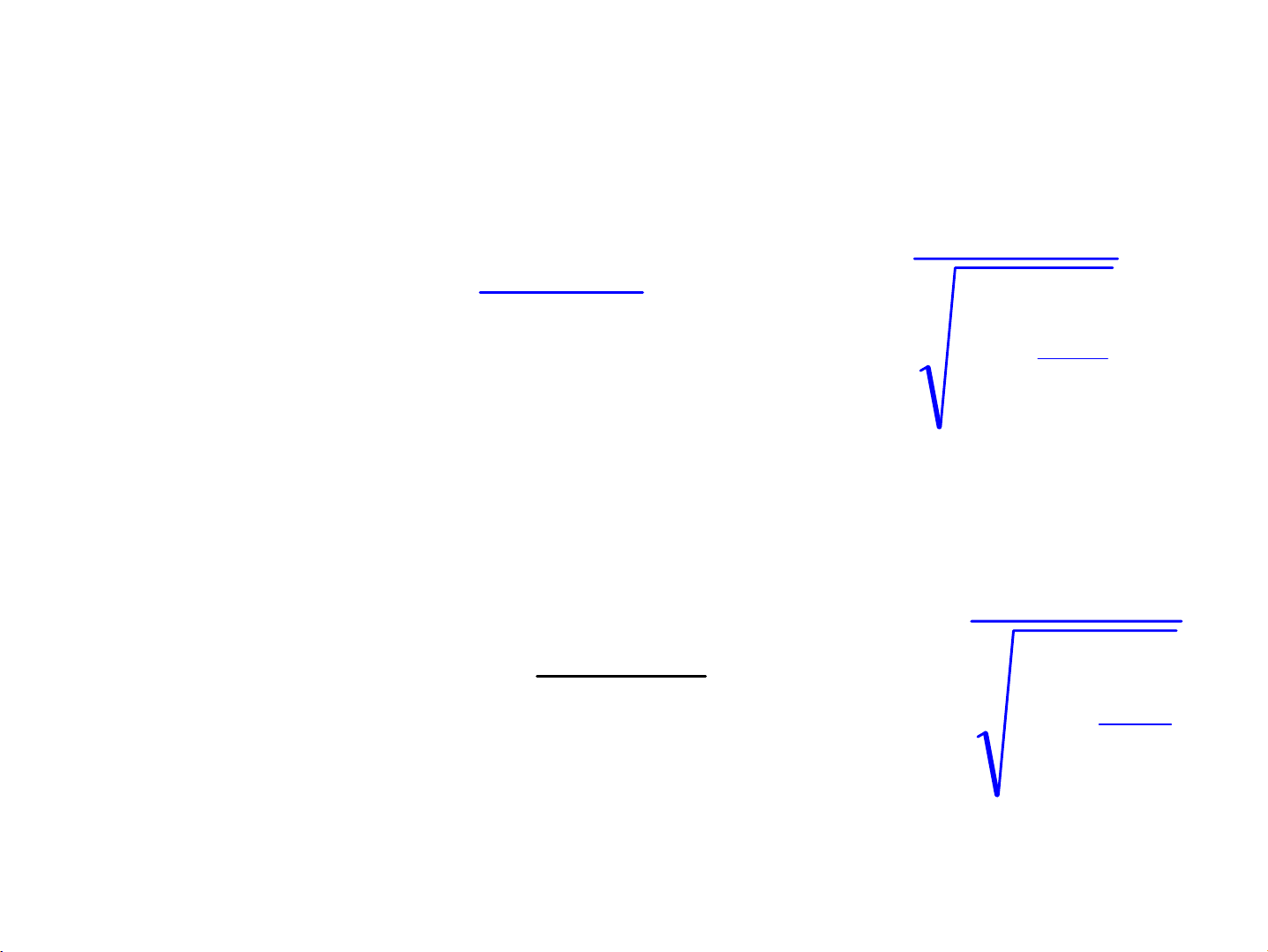
2
2
0
c
v
1
m
m
−
=
5. §éng lùc häc t−¬ng ®èi tÝnh
dt
)vm(d
F
r
r
=
dt
)vm(d
F
r
r
=
5.1. Ph−¬ng tr×nh c¬ b¶n cña chuyÓn ®éng
chÊt ®iÓm
m0- khèi l−îng nghØ (v=0)
5.2. §éng l−îng vμn¨ng l−îng
2
2
0
c
v
1
vm
vm
−
=
r
r
ds.FsdF|dA|dW ===
r
r
•N¨ngl−îng:
• §éng l−îng:
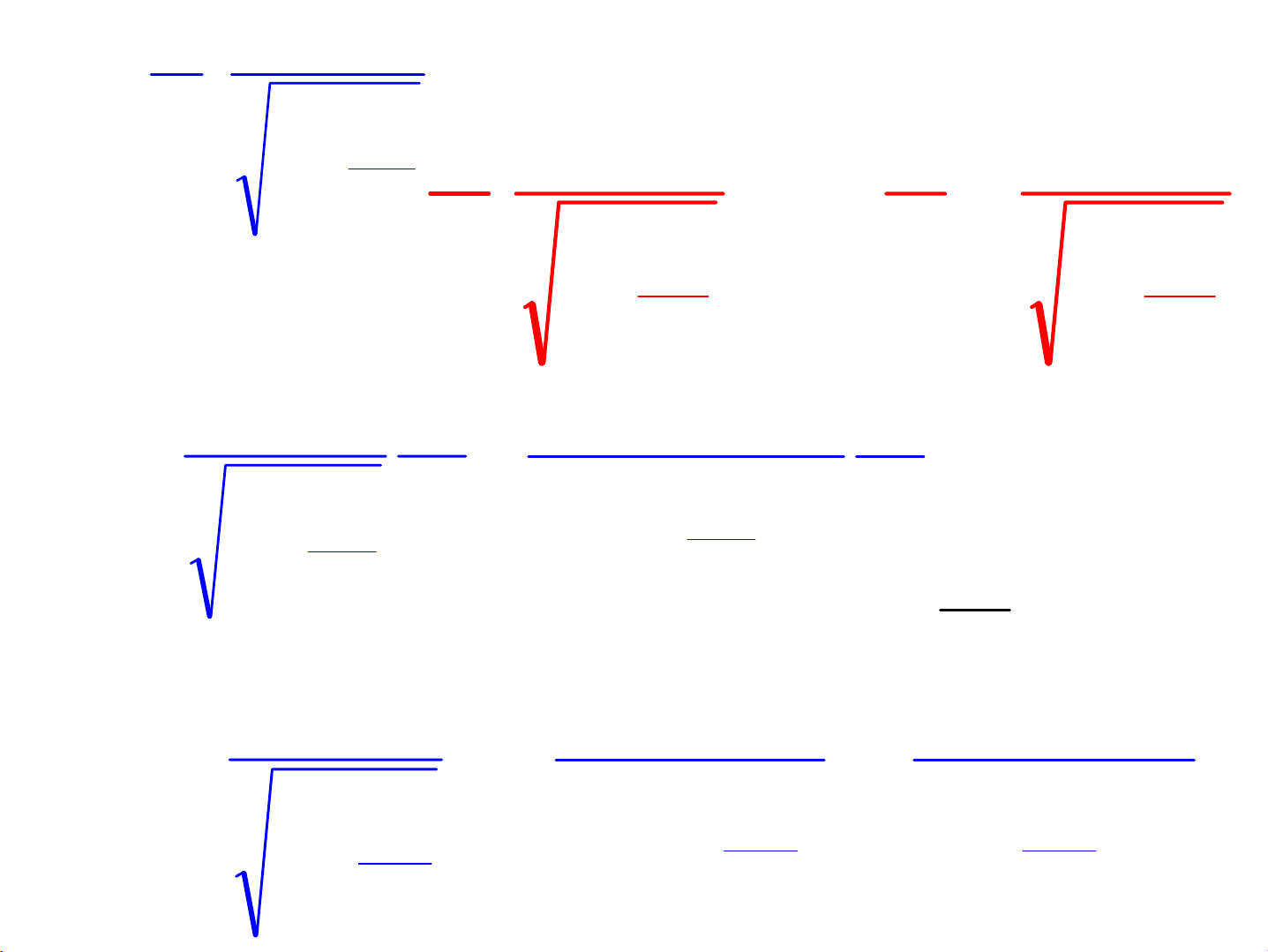
ds]
c
v
1
vm
[
dt
d
dW
2
2
0
−
=
ds]
dt
dv
)
c
v
1(c
vm
dt
dv
c
v
1
m
[dW
2/3
2
2
2
2
0
2
2
0
−
+
−
=
vdvds
dt
dv =
2/3
2
2
0
2
2
2
2
2
2
0
)
c
v
1(
vdvm
]
)
c
v
1(c
v
1[
c
v
1
vdvm
dW
−
=
−
+
−
=
]
c
v
1
1
.v[
dt
d
m]
c
v
1
vm
[
dt
d
2
2
0
2
2
0
−
=
−
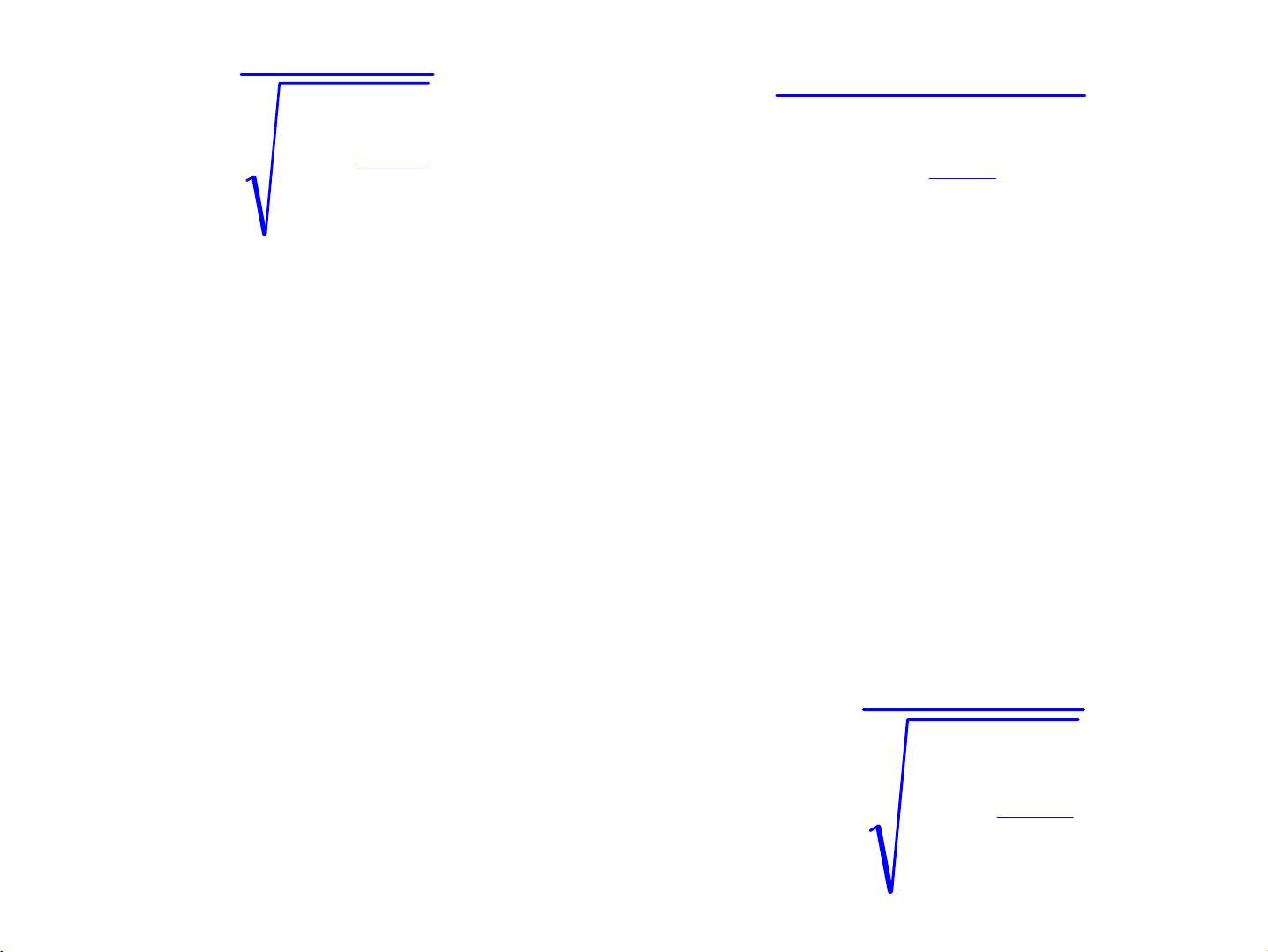
2
2
0
c
v
1
m
m
−
=
2/3
2
2
2
0
)
c
v
1(c
vdvm
dm
−
=
dmcdW 2
=
CmcW 2+=
0C;0m;0W
=
=
=
2
mcW =
☛HÖ thøc Anhxtanh:
• HÖ qu¶ ①§éng n¨ng:
)1
c
v
1
1
(cmcmmcW
2
2
2
0
2
0
2−
−
=−=
d
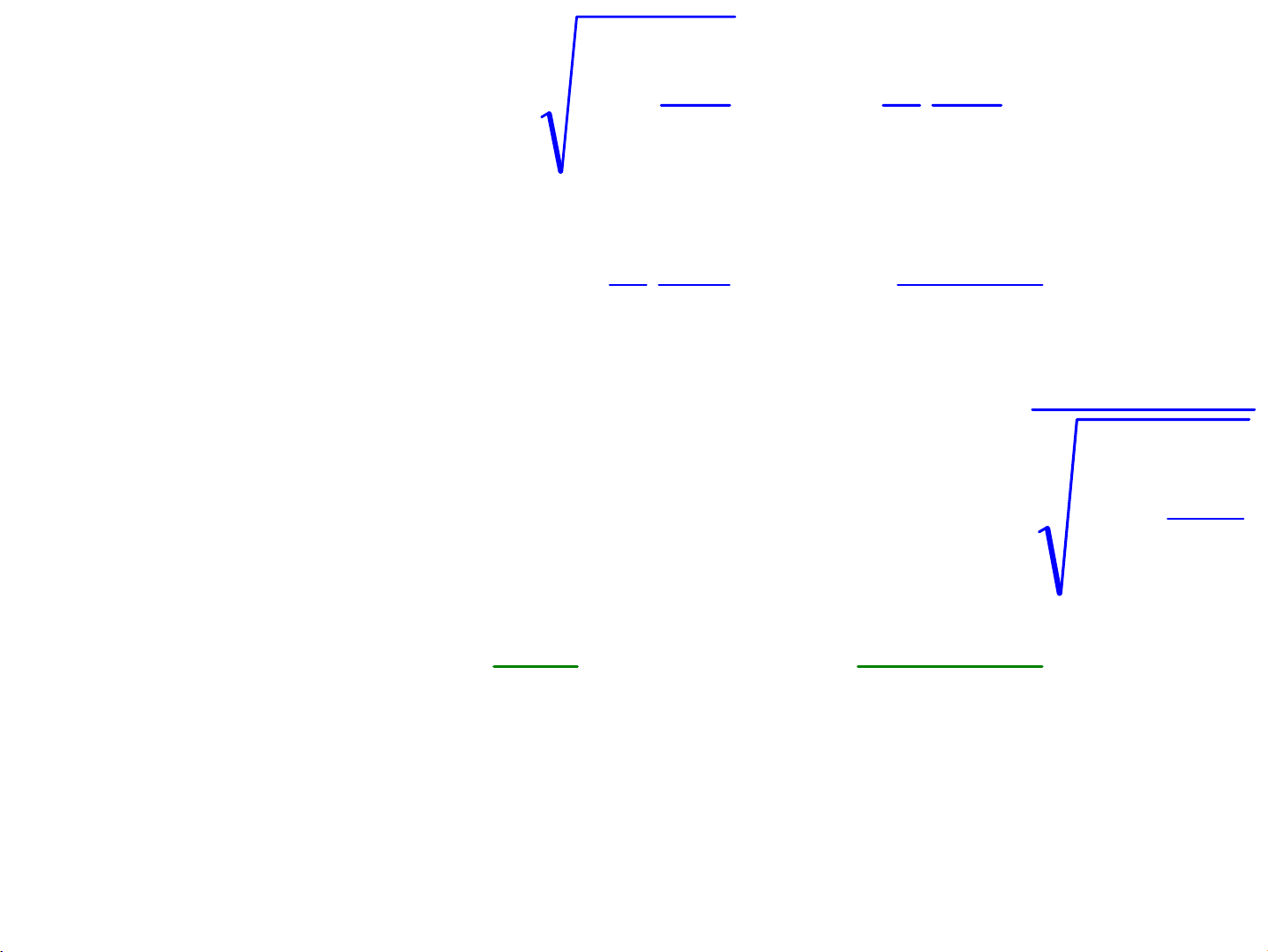
2
2
2
2
c
v
2
1
1
c
v
1−≈−
NÕu v<<c th×
2
vm
)1
c
v
2
1
1(cmW
2
0
2
2
2
0d ≈−+≈
②Quan hÖ gi÷a n¨ng
l−îng vμ®éng l−îng:
2
2
2
0
c
v
1
cm
W
−
=
2
22
2
2
2
24
0
2
c
vW
W)
c
v
1(Wcm −=−=
vmp vμ
r
== 2
mcW
2242
0
2cpc.mW +=