CHƯƠNG IV
THUYẾT TƯƠNG ĐỐI HẸP
Cơ học Newton (cơ học cổ điển) ra đời từ nữa
cuối thế kỷ XVII đóng vai trò hết sức to lớn.
Trong cơ học Newton người ta quan niệm không
gian có tính tuyệt đối và được mô tả bằng hình
học Euclide. Thời gian cũng có tính tuyệt đối.
Cuối thế kỷ 19 và đầu thế kỷ 20, khi nghiên cứu
đến những hiện tượng liên quan đến ánh sáng
hoặc những vận tốc lớn so sánh được với vận
tốc ánh sáng, người ta nhận thấy rằng những
khái niệm cũ không còn phù hợp nữa. Trong
tình hình đó, thuyết tương đối ra đời xây dựng
lại những khái niệm không gian và thời gian
khác hẳn với những khái niệm của Newton.
TTĐ Einstein gồm hai phần:
+ TTĐ hẹp ra đời 1905 nghiên cứu các HQC
quán tính.
+ TTĐ rộng ra đời 1916 nghiên cứu các HQC
không quán tính.
Trong phần này chúng ta chỉ nghiên cứu thuyết
tương đối hẹp.
I. Nguyên lý Galilê, phép biến đổi Galilê
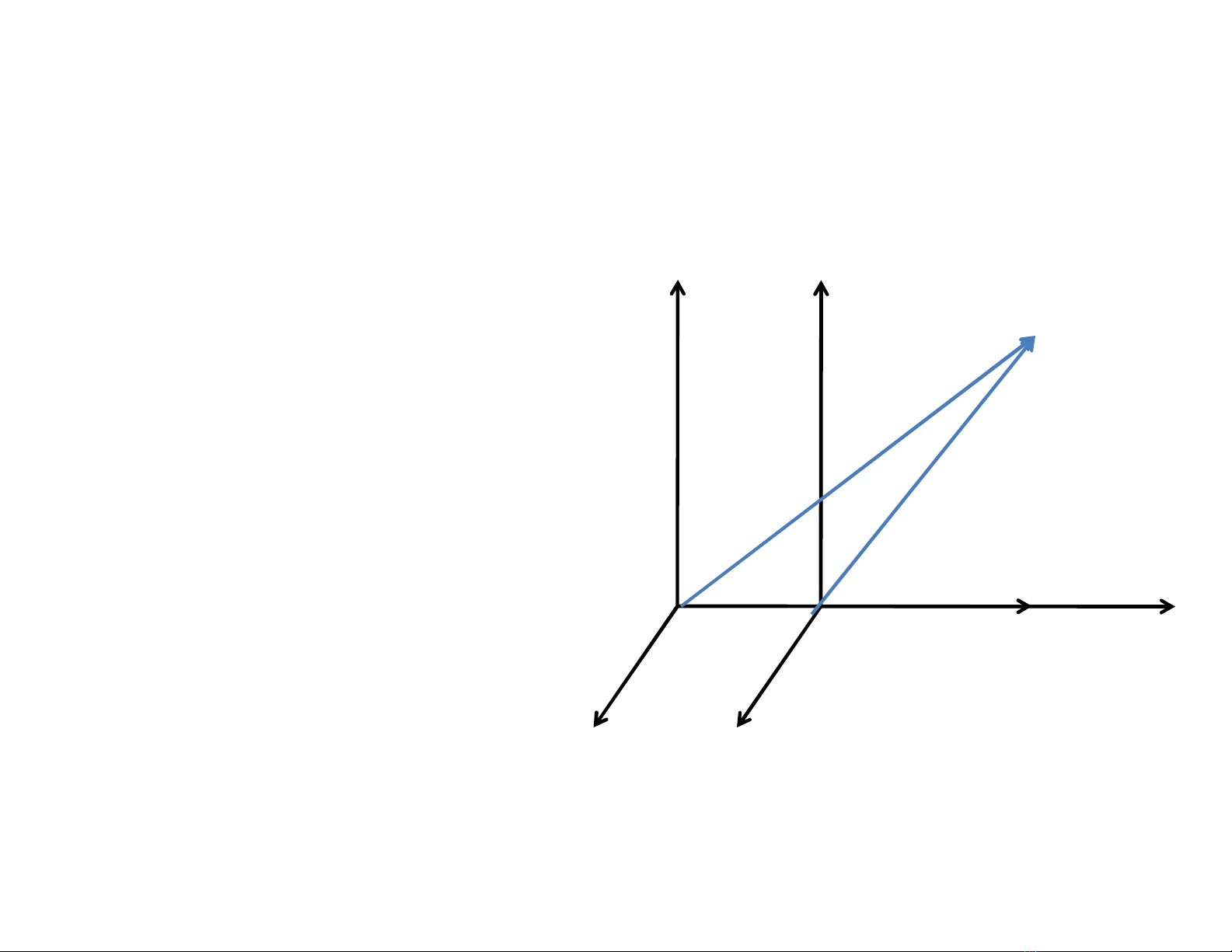
Giả sử ta có hệ K’ chuyển động đối với hệ K với
vận tốc không đổi dọc theo trục x và lúc đầu
gốc hai tọa độ trùng nhau. Khi đó ta có hệ thức:
Chiếu hệ thức trên xuống
các trục tọa độ ta được:
Các hệ thức này gọi là phép biến
đổi Galilée
v
y
OO’
z
y’
z’
xx’
KK’ M
r
'
r
r r OO r vt
' '
'
'
'
x x vt
y y
z z
t t
Phép biến đổi Gallilée dẫn đến một số KQ sau:
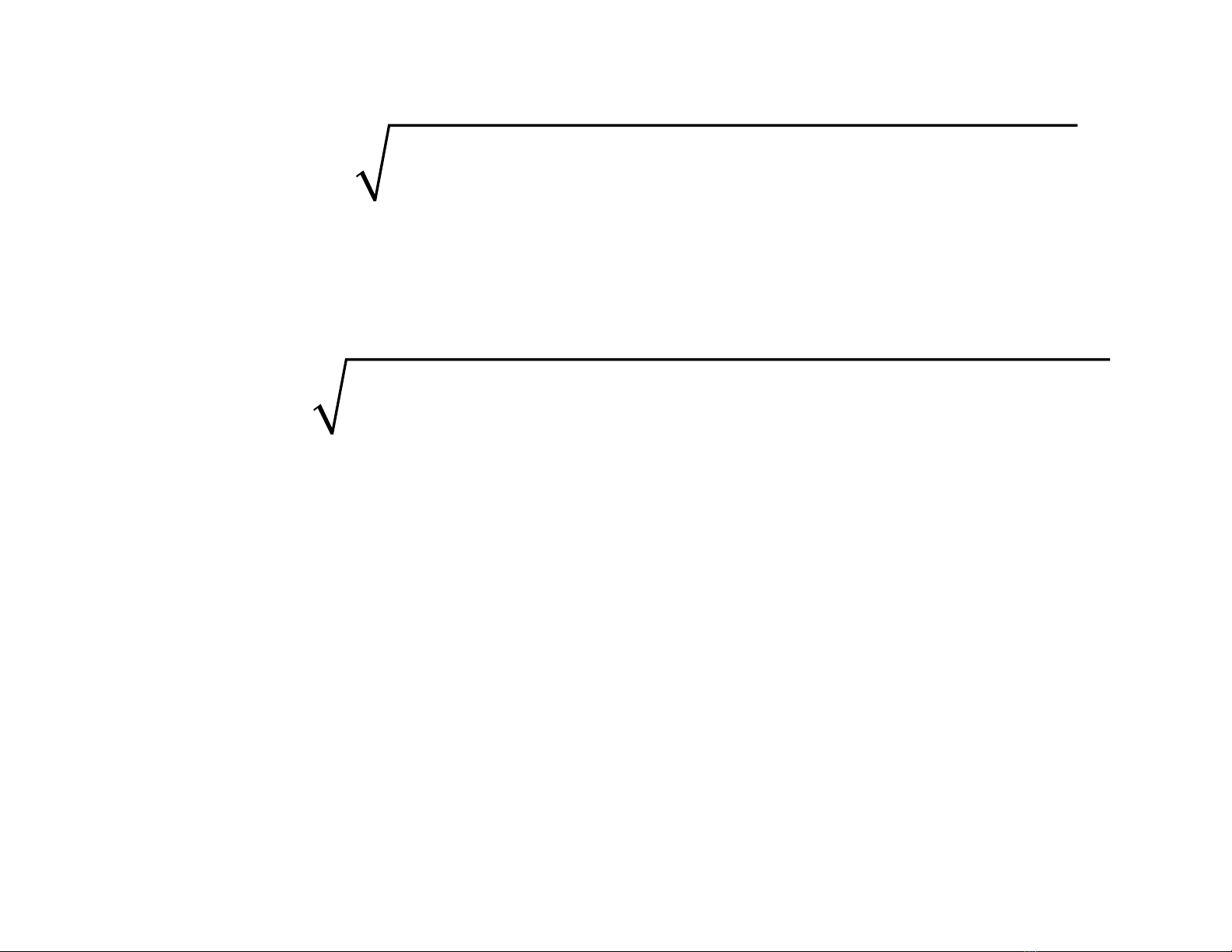
a) Gọi
là khoảng cách giữa hai điểm 1, 2 trong hệ K;
khoảng cách tương ứng trong hệ K’ là:
Ta có : : khoảng cách giữa hai điểm
là đại lượng bất biến .
Lấy đạo hàm các hệ thức trên theo thời gian
Các hệ thức này là phép cộng vận tốc cổ điển.
2 2 2
1 2 1 2 1 2
( ) ( ) ( )
l x x y y z z
2 2 2
1 2 1 2 1 2
' ( ' ' ) ( ' ' ) ( ' ' )
l x x y y z z
'
l l
' ; ' ; '
x x y y z z
u u v u u u u