Trường THPT Phan Ngọc Hiển ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC: 2012-2013
Môn : Toán lớp 12 ( cơ bản )
Thời gian : 90 phút
Bài 1:(4 điểm) 1/ Khảo sát và vẽ đồ thị hàm số: 32
3
y
xx=− có đồ thị (C);
2/ Dựa vào đồ thị (C), biện luận theo m số nghiệm phương trình:
32
30xxm−−=
.
Bài 2: (2 điểm) Giải các phương trình:
1/ 22
29.220
xx+−+=
2/
()
243
log 1 2log 3.log 1
x
x−+ =
Bài 3: (1 điểm) Tìm m để giá trị lớn nhất của hàm số f(x) =
()
22;1
1
xm m m
x
−+ ≠
+ trên đoạn
[
]
0;1 bằng 1−.
Bài 4: (1 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA
vuông góc với mặt phẳng đáy và cạnh bên SB = 3a. Tính thể tích của khối chóp S.ABCD
theo a .
Bài 5: ( 2 điểm) Tìm m để hàm số y =
()
32
13925
3xm x xm
+
−−+−
có cực đại, cực tiểu và các
điểm này cách đều trục tung.
-------------------------------
Đáp án: ( Đề cơ bản )
Bài
1
4
điểm
1. (C): 32
3
y
xx=−
TXĐ: D =
¡
()
,2
363 2yxxxx=−= −
,00
024
xy
yxy
=⇒=
⎡
=⇔
⎢=⇒=−
⎣
()
,, 666 1yx x=−= −
,, 01 2yxy=⇔=⇒=−
Ö (C) có điểm uốn U(1; -2)
lim ; lim
xx
yy
→−∞ →+∞
=−∞ =+∞
BBT:
x - ∞ 0 2 + ∞
y/ + 0 - 0 +
y 0 +
∞
- ∞ CĐ -4
CT
KL…
Đồ thị nhận điểm uốn làm tâm đối
0.25
0.25
0.5
0.5
0.5
Bài
2
2
điểm
1/ 22
29.220
xx+−+=
Ù2
4.2 9.2 2 0
xx
−+=
Đặt t = 20
x>
PT Ù 2
4920tt−+=
Ù
2
1
4
t
t
=
⎡
⎢
⎢=
⎣
(nhận)
* t = 2 Ù22 1
x
x
= <=> =
* t = 1
4 Ù1
22
4
xx=<=>=−
Vậy: PT có nghiệm x = 1;
x = -2
2/
(
)
243
log 1 2log 3.log 1
x
x
−
+=
ĐK: x > 0
PTÙ
()
24
log 1 2 log 1
x
x−+ =
Ù
()
22
log 1 log 1
x
x−+ =
0.25
0.25
0.25
0.25
0.25
0.25
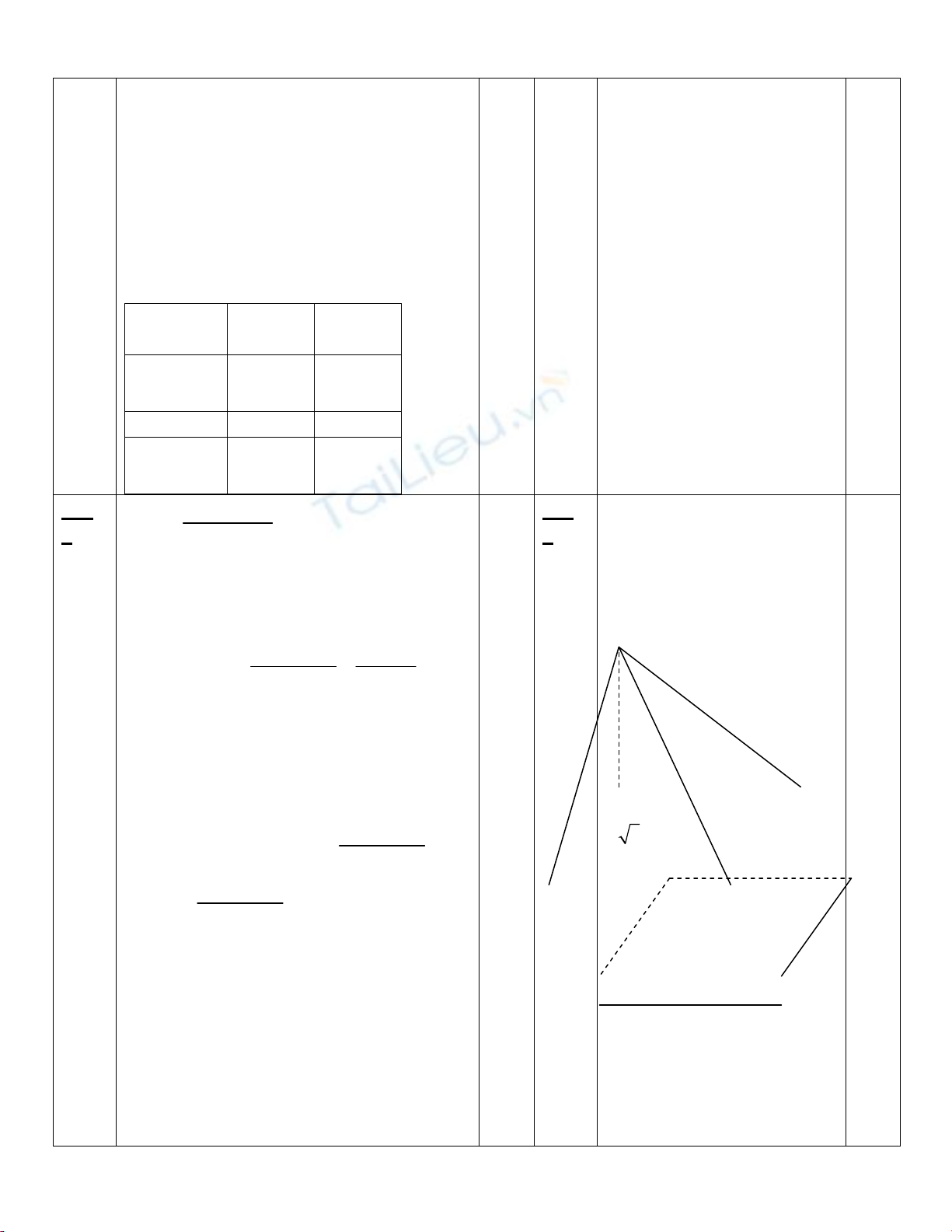
xứng
Cho x = -1=> y = -4
x = 3 => y = 0
vẽ đồ thị…
2. PT: 32
30xxm−−=
32
3
x
xm⇔− =
Số nghiệm của PT là số giao điểm của
đồ thi (C) và đường thẳng d: y = m
Dựa vào (C) ta có:
m ()dC∩ Nghiệm
PT
0
4
m
m
>
⎡
⎢<−
⎣ 1 1
40m−< < 3 3
0
4
m
m
=
⎡
⎢=−
⎣
2
2
0.5
0.5
0.25
0.25
0.5
Ù
()
2
log 1 1xx−=
Ù
()
12xx−=
Ù220xx−−=
Ù
()
()
1
2
x
L
x
N
=−⎡
⎢=
⎣
Vậy: PT có nghiệm x = 2
0.25
0.25
Bài
3
1
điểm
f(x) =
22
1
x
mm
x
−+
+
TXĐ: D =
{
}
\1−¡
Ö hàm số liên tục trên D
Ö hàm số liên tục trên
[
]
0;1
Ta có:
() ()
()
()
2
2
,
22
1
21 0
11
m
mm
fx
xx
−
−+
==>
++
Với mọi m khác 1;
{
}
\1x∀∈ −¡
Ö Hàm số đồng biến trên
()()
;1 1;−∞ − ∪ − +∞
Ö Hàm số đồng biến trên
[
]
0;1
Ö
()
[]
()
2
0;1
12
12
mm
Maxf x f +−
==
Ö 2
12 1
2
mm+−=−
Ù 2230mm−−=
Ù1
3
m
m
=−
⎡
⎢=
⎣( thỏa ĐK)
Vậy: 1; 3mm=− =
0.25
0.25
0.25
0.25
Bài
4
1
điểm
3a
a
A
B
D
C
Ta có:
(
)
SA ABCD⊥=> SA AB
⊥
0.25
0.25
0.25
0.25
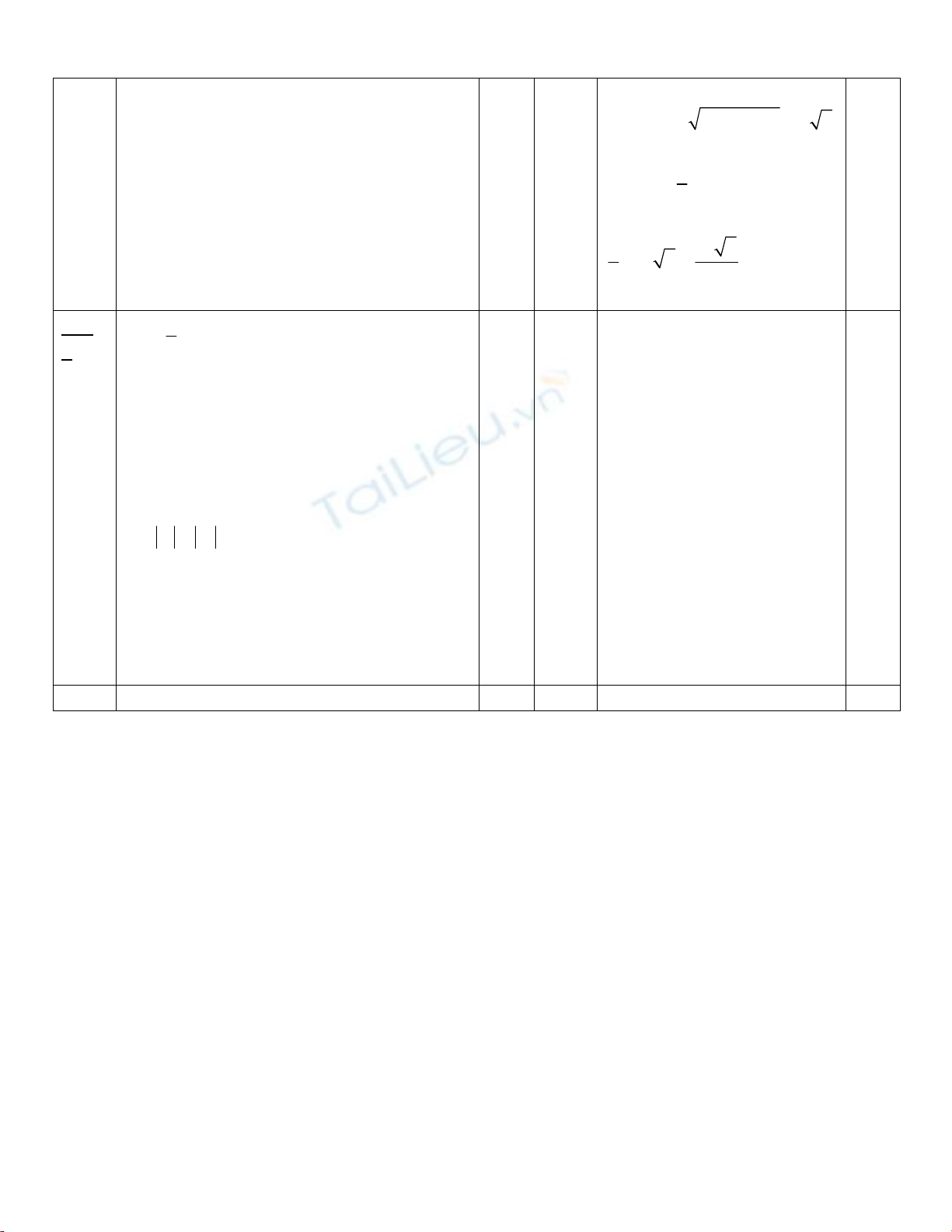
=> SAB
Δ
vuông tại A
=> 22 2SA SB AB a=−=
Thể tích :
.
1.
3
S ABCD ABCD
VSSA=W
=
2
1.2
3aa =
32
3
a
Bài
5
2
điểm
Y =
()
32
13925
3xm x xm
+− −+−
Ta có:
()
,2
239yx m x=+ − −
,0y= Ù
()
(
)
22390*xmx+−−=
PT (*) luôn có 2 nghiệm phân biệt
( do a.c < 0 ) nên hàm số luôn có hai
cực trị x1; x2
Hai cực trị này cách đều trục tung
Ù 12
x
x=
Ù 12
x
x=− (vì 12
x
x≠)
Ù 12
0xx+=
Ù 30m−=
Ù 3m=
Vậy: 3m=
0.5
0.25
0.25
0.25
0.25
0.25
0.25
S
Trường THPT Phan Ngọc Hiển ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC: 2012-2013
Môn : Toán lớp 12 ( Nâng cao)
Thời gian : 90 phút
Bài 1: ( 4 điểm) 1/ Khảo sát và vẽ đồ thị hàm số: 32
3yx x=− có đồ thị (C);
2/ Dựa vào đồ thị (C), biện luận theo m số nghiệm phương trình:
32
30xxm−−=.
Bài 2: ( 2 điểm)
1/ Tính:
(
)
(
)
(
)
00 0
22 2
log tan1 log tan 2 ... log tan 89M=+ ++
2/ Cho 25 2
log 7 ; log 5ab==. Tính 35
49
log 8 theo ;ab.
Bài 3: ( 1 điểm) Tìm m để giá trị lớn nhất của hàm số f(x) =
()
22;1
1
xm m m
x
−+ ≠
+
trên đoạn
[
]
0;1 bằng 1−.
Bài 4: ( 1 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a,cạnh bên SA
vuông góc với mặt phẳng đáy và cạnh bên SB = 3a. Gọi I là trung điểm SB. Tính thể tích
của khối chóp I.BCD theo a .
Bài 5: ( 2 điểm) Tìm m để đồ thị hàm số y =
()
()
322
12 1 5 6 2012
3xmxmmx−+ +−++ có cực
đại, cực tiểu nằm về hai phía đối với trục tung.
-----------------------------------------------
Đáp án: ( Nâng cao)
Bài
1
4
điểm
1. (C): 32
3yx x=−
TXĐ: D =
¡
(
)
,2
363 2yxxxx=−= −
,00
024
xy
yxy
=⇒=
⎡
=⇔
⎢=⇒=−
⎣
(
)
,, 666 1yx x=−= −
,, 01 2yxy=⇔=⇒=−
Ö (C) có điểm uốn U(1; -2)
lim ; lim
xx
yy
→−∞ →+∞
=−∞ =+∞
BBT:
x - ∞ 0 2 + ∞
y/ + 0 - 0 +
y 0 + ∞
- ∞ CĐ -4
CT
KL…
Đồ thị nhận điểm uốn làm tâm đối xứng
Cho x = -1=> y = -4
x = 3 => y = 0
vẽ đồ thị…
2. PT: 32
30xxm−−=
0.25
0.25
0.5
0.5
0.5
0.5
0.5
Bài
2
2
điểm
1/ Ta có:
(
)
(
)
()
00
22
00
22
log tan1 log tan 89
log tan1 .cot1 log 1 0
+=
=
==
Tương tự:
(
)( )
()
00
22
00
22
log tan 2 log tan 88
log tan 2 .cot 2 log 1 0
+=
=
==
…
Có 44 cặp như vậy và dư ra
(
)
0
22
log tan 45 log 1 0==
Vậy: 0P
=
2/ Xét:
35
49
log 8=
()
555
49
3log 3 2log 7 3log 2
8
== −
Ta có:
25 5
25
2 2 log 7 log 7 ;
1
log 5 log 2
a
bb
==
=
=> =
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
32
3
x
xm⇔− =
Số nghiệm của PT là số giao điểm của đồ
thi (C) và đường thẳng d: y = m
Dựa vào (C) ta có:
m ()dC∩ Nghiệm
PT
0
4
m
m
>
⎡
⎢<−
⎣ 1 1
40m−< < 3 3
0
4
m
m
=
⎡
⎢=−
⎣
2
2
0.25
0.25
0.5
Vậy: 35
49
log 8= 3
34
ab
⎛⎞
−
⎜⎟
⎝⎠
Bài
3
1
điểm
f(x) =
22
1
x
mm
x
−+
+
TXĐ: D =
{
}
\1−¡
Ö hàm số liên tục trên D
Ö hàm số liên tục trên
[
]
0;1
Ta có:
() ()
()
()
2
2
,
22
1
21 0
11
m
mm
fx xx
−
−+
==>
++
Với mọi m khác 1;
{
}
\1x∀∈ −¡
Ö Hàm số đồng biến trên
(
)
(
)
;1 1;−∞ − ∪ − +∞
Ö Hàm số đồng biến trên
[
]
0;1
Ö
()
[]
()
2
0;1
12
12
mm
Maxf x f +−
==
Ö 2
12 1
2
mm+−=−
Ù 2230mm−−=
Ù1
3
m
m
=−
⎡
⎢=
⎣ ( thỏa ĐK)
Vậy: 1; 3mm=− =
0.25
0.25
0.25
0.25
Bài
4
1
điểm
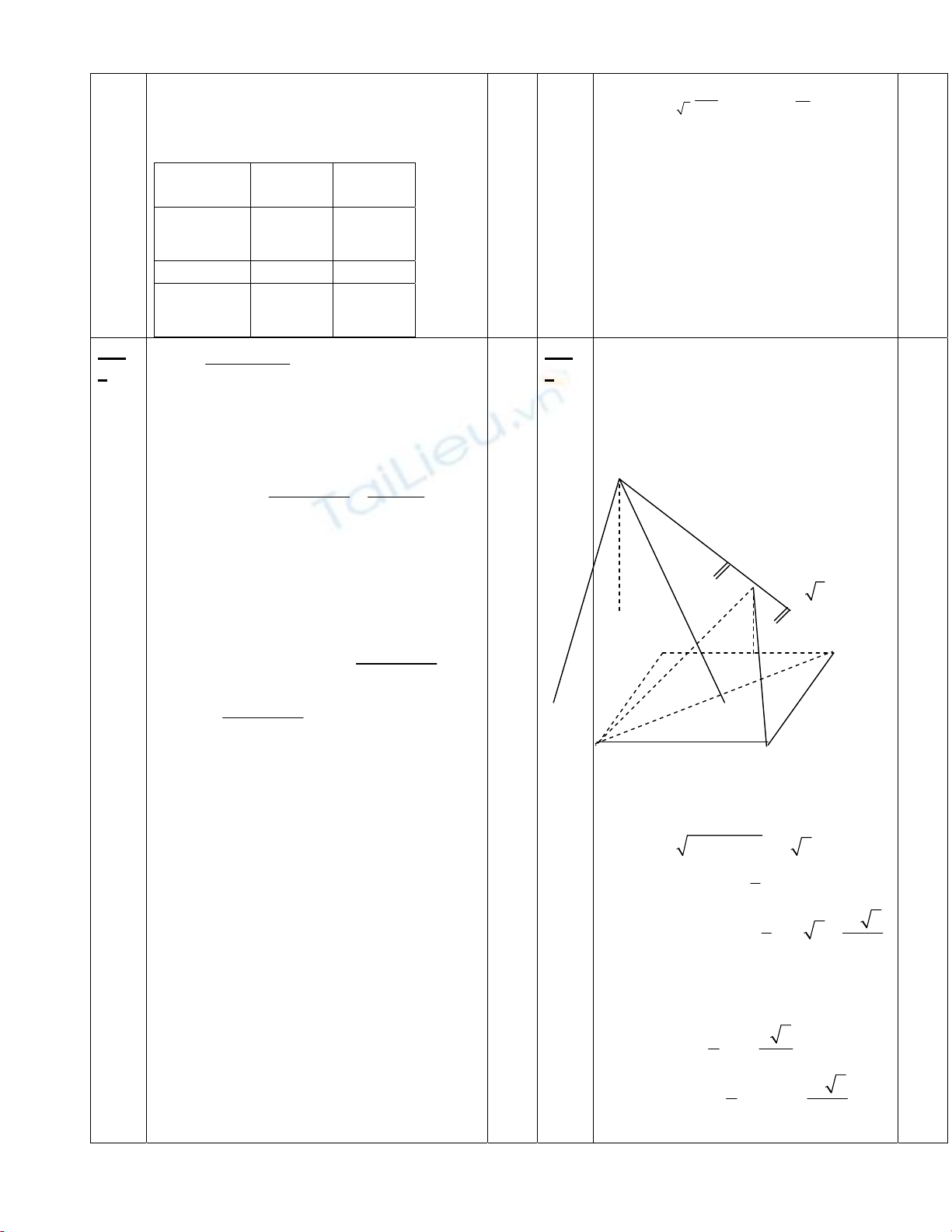
S
I 3a
A H B
D C
Ta có:
(
)
SA ABCD⊥=> SA AB
⊥
=> SAB
Δ
vuông tại A
=> 22 2SA SB AB a=−=
Thể tích : .
1.
3
S ABCD ABCD
VSSA=W
= 2
1.2
3aa =
32
3
a
Gọi H là trung điểm AB
Ö IH là đường trung bình của
SABΔ
Ö 12
22
a
IH SA==
Ö 3
..
12
.
412
I BCD S ABCD
a
VV==
0.25
0.25
0.25
0.25












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



