1
Gi ng viên: Th.s Nguy n Th Thu Ngaả ễ ị
BAI GIANG
HINH HOC HOA HINH
2
Bai 3
Măt phăng
3
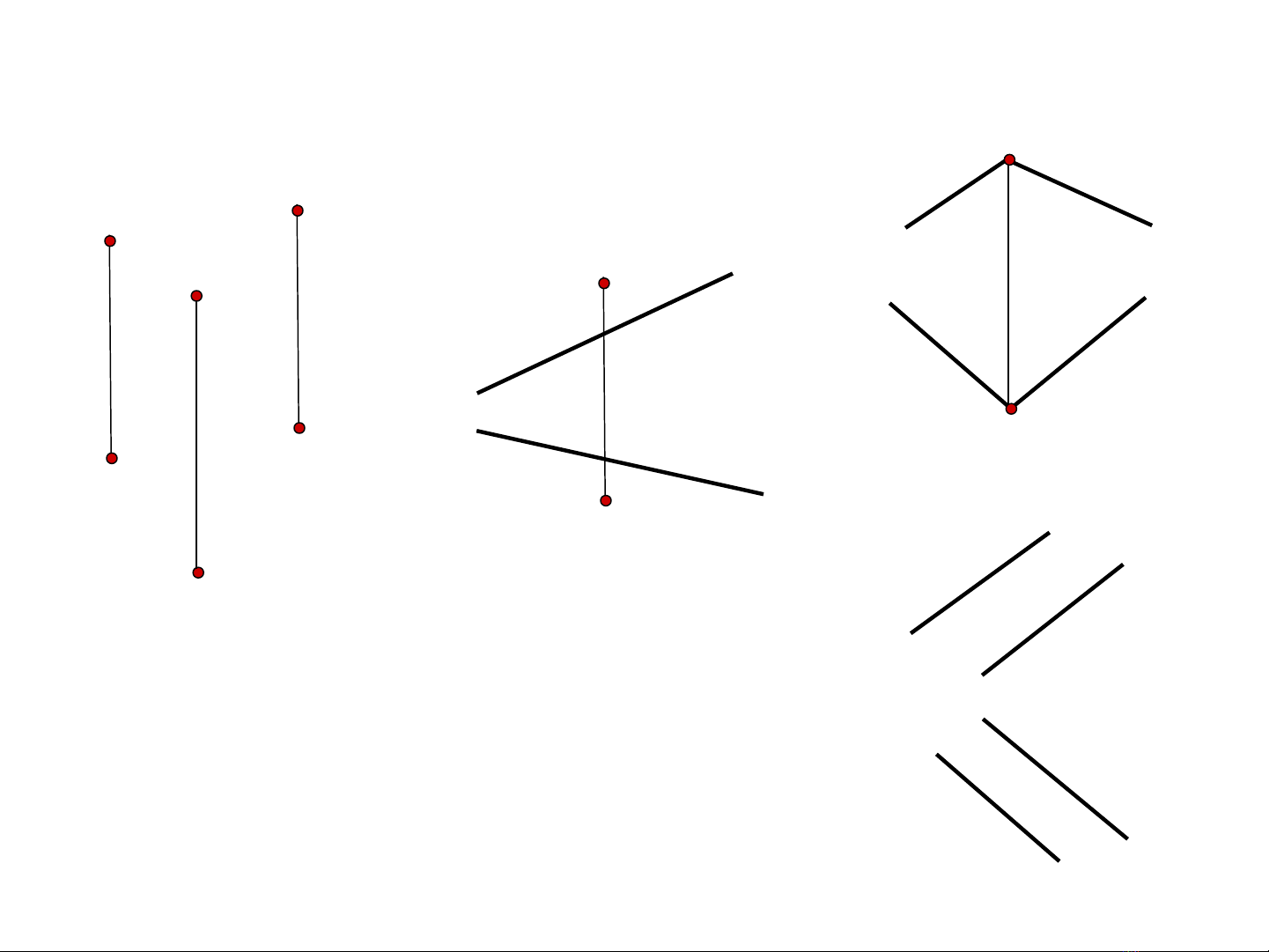
I- Đ th c c a m t m t ph ngồ ứ ủ ộ ặ ẳ
Trên đ th c có 4 cách đ xác đ nh m t m t ph ng ồ ứ ể ị ộ ặ ẳ
A1l1
l2
A2
A1
A2
B1
B2
C1
C2
Hình 3.1.Đô th c cua măt phăng ư
I1
b1
b2
I2
a1
a2
d1
d2
c1
c2
a)
d)
c)
b)
Chú ý:
T cách xac đinh măt phăng này có th chuy n đ i thành ừ ể ể ổ
cách xac đinh khác. Do đó ph ng pháp gi i bài toán không ươ ả
ph thu c vào cách cho m t ph ngụ ộ ặ ẳ
4
II- V t c a m t ph ngế ủ ặ ẳ
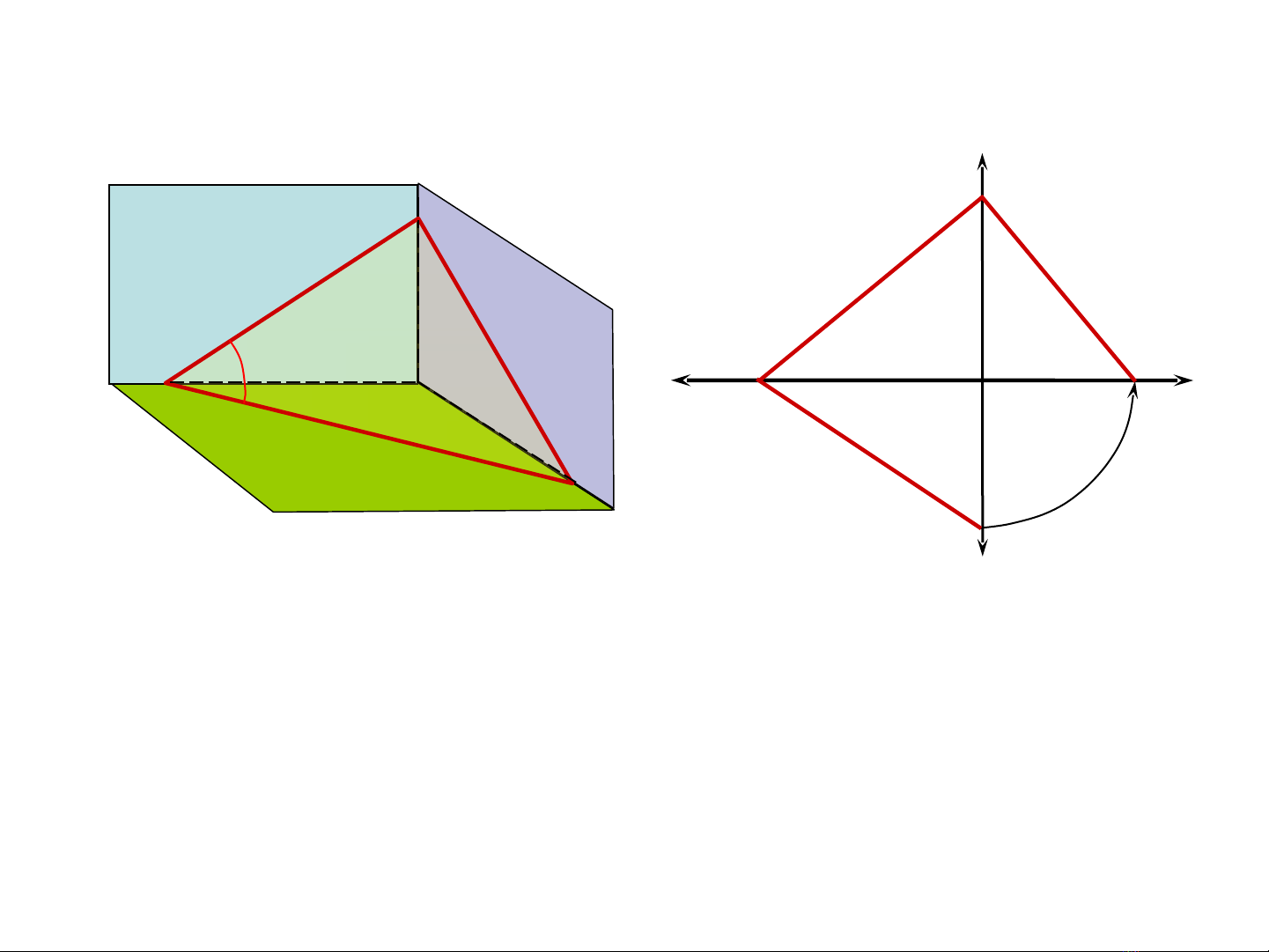
V t c a m t ph ng là giao tuy n c a c a m t ph ng đo v i các m t ph ng hình chi u ế ủ ặ ẳ ế ủ ủ ặ ẳ ớ ặ ẳ ế
Cho m t ph ng (α):ặ ẳ
* V t đ ng m: m ≡ (α) ∩ Пế ứ 1
* V t b ng n: n ≡ (α) ∩ Пế ằ 2
* V t c nh p: p ≡ (α) ∩ Пế ạ 3
Đ phân bi t các m t ph ng ta vi t tên v t c a m t ph ng kèm theo tên c a m t ph ng ể ệ ặ ẳ ế ế ủ ặ ẳ ủ ặ ẳ
đó.
Ví d : M t ph ng (α) → -V t đ ng : mụ ặ ẳ ế ứ α
-V t b ng : nế ằ α
ế ạ
x
Π1
Π3
y
Π2
p
m
n
z
x
z
y
O
m=m1
p=p3
n=n2
m2=n1=p2
p1
Hình 3.2. V t c a m t ph ngế ủ ặ ẳ
O
y
mα
nα
pα
α
5
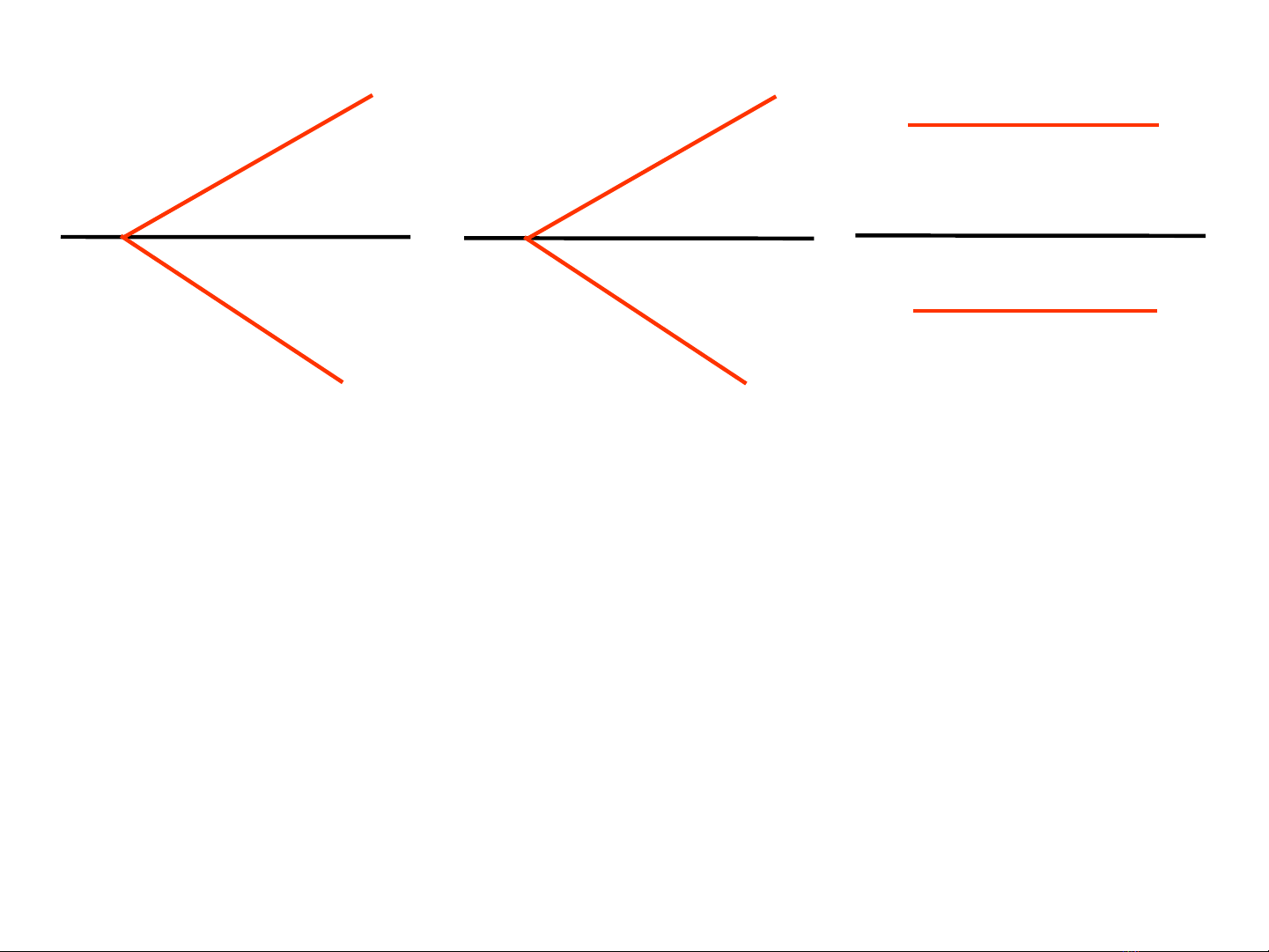
- Ta có th cho m t ph ng b i các v t c a nó. M t ph ng có hai v t c t nhau t i ể ặ ẳ ở ế ủ ặ ẳ ế ắ ạ
αx∈ x (Hình 3.3a,b) ho c m t ph ng có v t song song v i tr c x (Hình 3.3c)ặ ặ ẳ ế ớ ụ
- Thông th ng ng i ta ch th hi n v t đ ng và v t b ng c a m t ph ngườ ườ ỉ ể ệ ế ứ ế ằ ủ ặ ẳ
- Đ ch v t đ ng và v t b ng c a m t ph ng ng i ta có th dùng ký hi u mể ỉ ế ứ ế ằ ủ ặ ẳ ườ ể ệ 1,
m2
và n1,n2 (Hình 3.3a)
- Đ ch v t đ ng và v t b ng c a m t ph ng α ta kèm theo tên c a m t ph ng ể ỉ ế ứ ế ằ ủ ặ ẳ ủ ặ ẳ
đó
ký hi u mệα, nα (Hình 3.3b,c)
x
m1
n2
x
mα
nα
αxx
mα
nα
a) c)
b)
Hình 3.3. M t s cách cho m t ph ng b ng v t trên đ th cộ ố ặ ẳ ằ ế ồ ứ
αxm2=n1=x