1Lecture 2
BÀI GIẢNG
Biến Đổi Năng Lượng Điện Cơ
TS. HồPhạm Huy Ánh
March 2010
http://www4.hcmut.edu.vn/~hphanh/teach.html
2Lecture 2
¾Điện áp ba pha trong lưới điện xoay chiều ba pha cân bằng thứtự
thuận (kí hiệu a-b-c) được biểu diễn như sau:
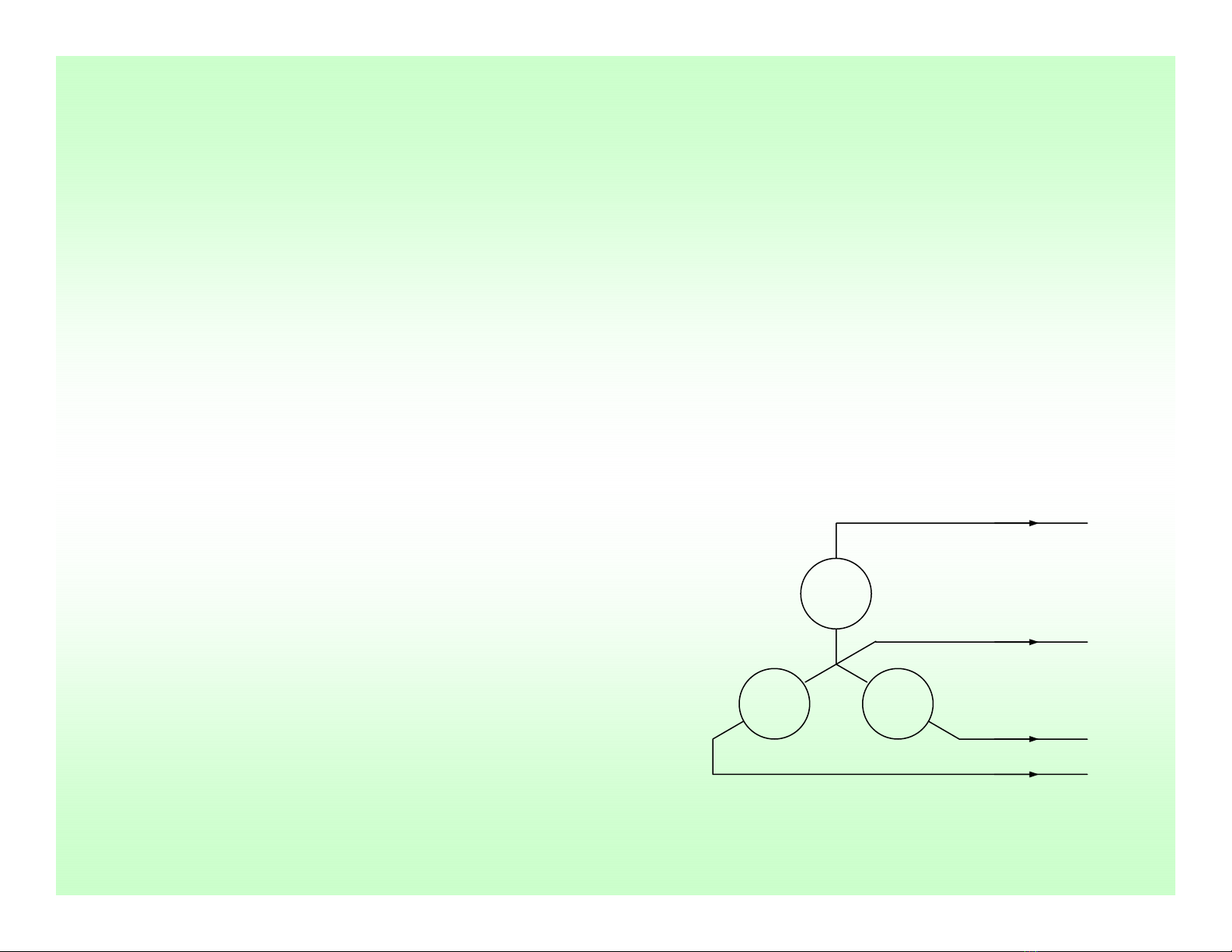
HệThống Điện Xoay Chiều Ba Pha
¾Điện xoay chiều ba pha có hai cách mắc: ĐấuY vàĐấuΔ
Vớiđấu Y, 3 ngõ a’, b’, và c’ đượcchập chung cho ta đầu ra trung tính n.
()
tVv maa
ω
cos
'=
(
)
0
'120cos −= tVv mbb
ω
(
)
0
'120cos += tVv mcc
ω
Ba thành phần dòng ia, ib, và iclà ba
dòng dây đượccấptừba nguồn pha
tương ứng. inlà dòng dây trung tính.
ia
in
ib
ic
a
b
c
n
+
−
+
−
+
−
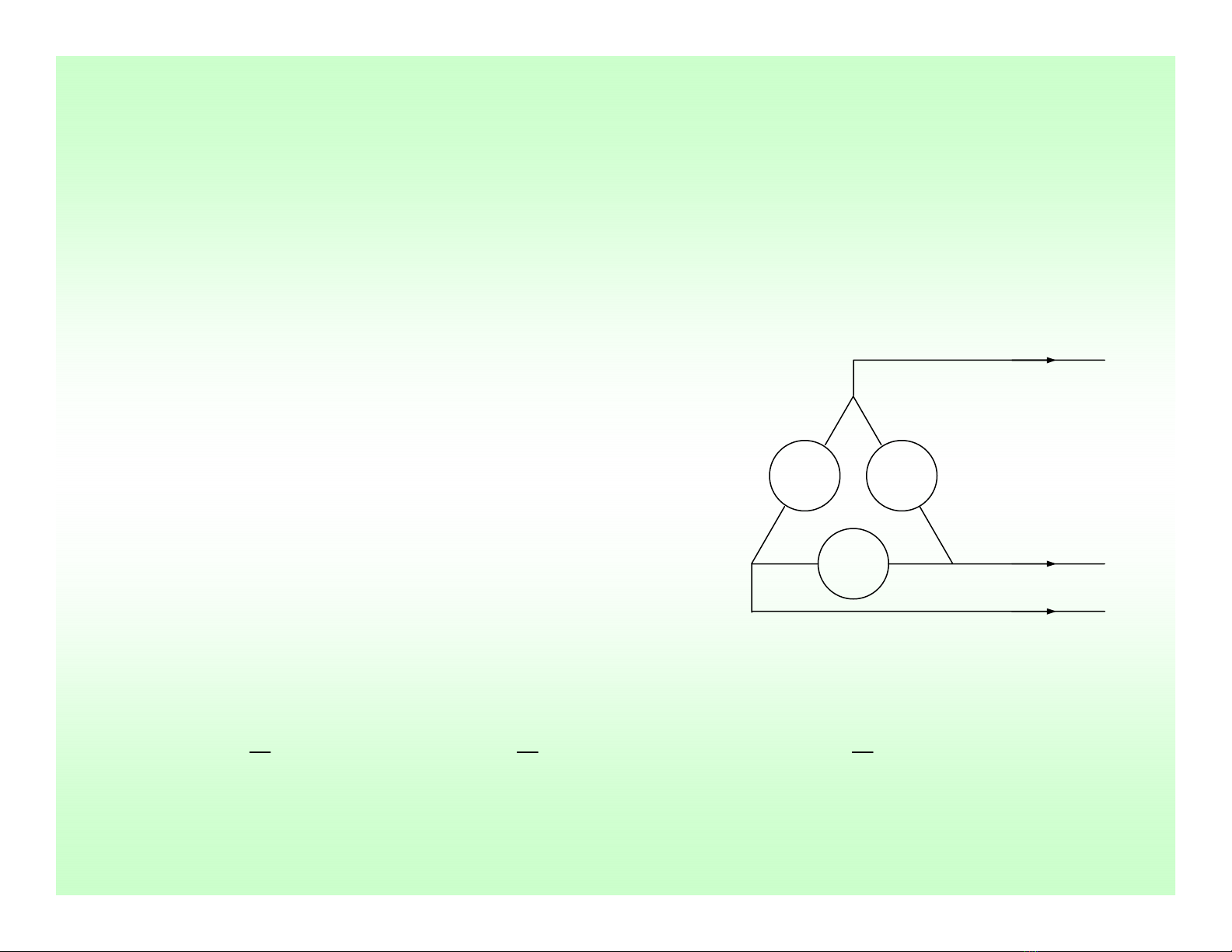
3Lecture 2
VớiđấuΔ, a’ đượcđấuvớib, b’ đượcđấuvớic. Vì vac’ = vaa’(t) + vbb’(t) +
vcc’(t) = 0, nhưđãkiểmchứng qua biểuthứclượng giác, nên c’ đượcđấu
vớia.
ia
ib
ic
a
b
c
c’
a’
b’
+
−
+
−
+
−
¾Các đạilượng DÂY và PHA
Vì cảnguồnvàtải ba pha đềucóthể
đượcĐấu Y hay ĐấuΔ, lưới điện xoay
chiều ba pha có tổng cộng bốn kiểu kết
nối(nguồn-tải): Y-Y; Y-Δ; Δ-Y và Δ-Δ.
•Lưới điện xoay chiều ba pha cân bằng thứtựthuậnY-Y:
0
0∠=
φ
VVan
0
120−∠=
φ
VVbn
0
120∠=
φ
VVcn
HệThống Điện Xoay Chiều Ba Pha (tt)
4Lecture 2
VớiV
φ
là giá trịđiện áp pha hiệudụng giữa pha và trung tính.
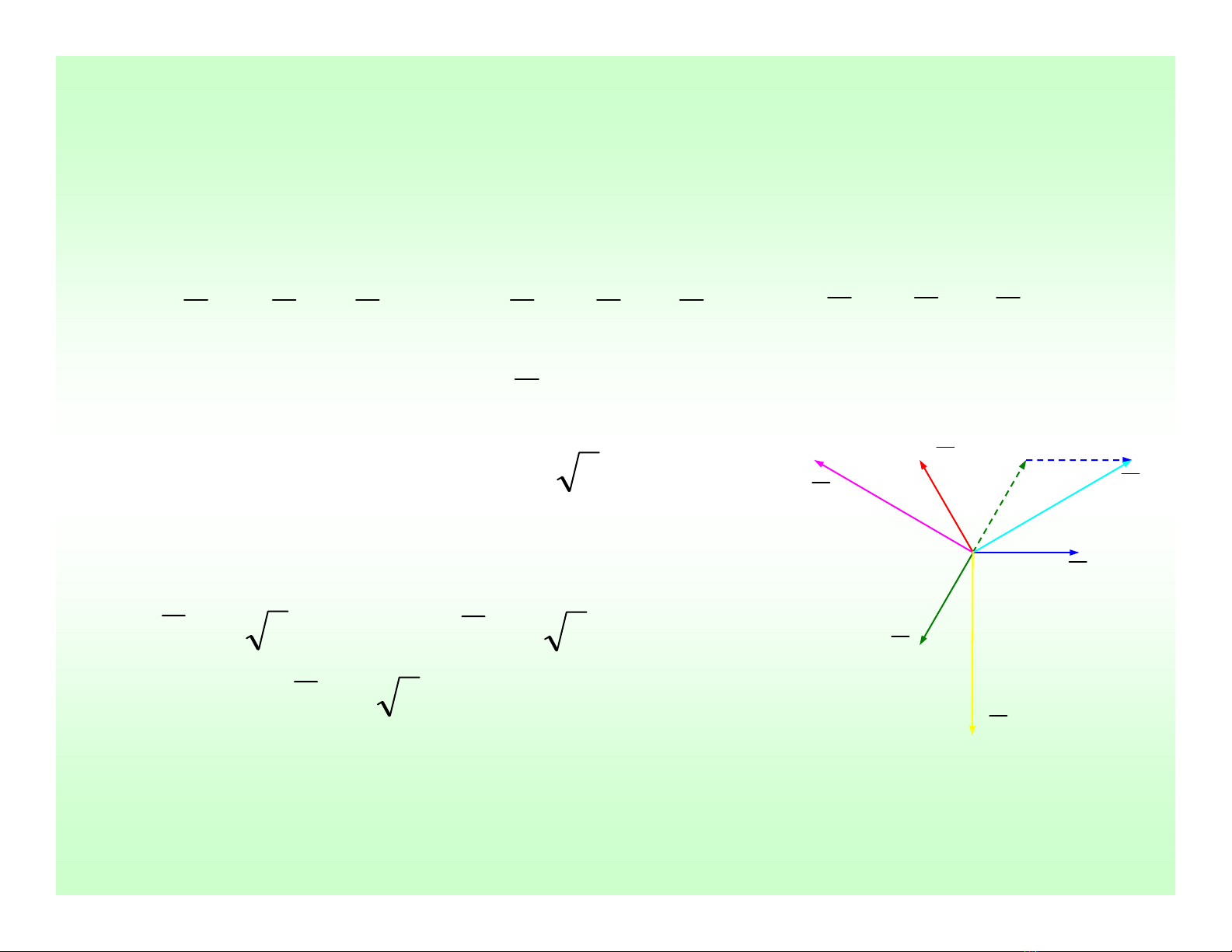
Điệnápgiữa hai pha gọilàápdâyđượcxácđịnh nhưsau:
bnanab VVV −= cnbnbc VVV −= ancnca VVV −=
Cụthểđộlớncủa áp dây có thểxác định:
ab
V
(
)
φφ
VVVab 330cos2 0==
an
V
bn
V
cn
V
ab
V
bc
V
ca
V
Từđó, dùng giảnđồ vector, ta xác định được:
0
303 ∠=
φ
VVab
0
903 −∠=
φ
VVbc
0
1503 ∠=
φ
VVca
Ta cũng dễdàng chứng minh được, in= 0 (ba pha cân
bằng không có dòng trung tính)
HệThống Điện Xoay Chiều Ba Pha (tt)
5Lecture 2
Không mấttínhtổng quát, ta có:
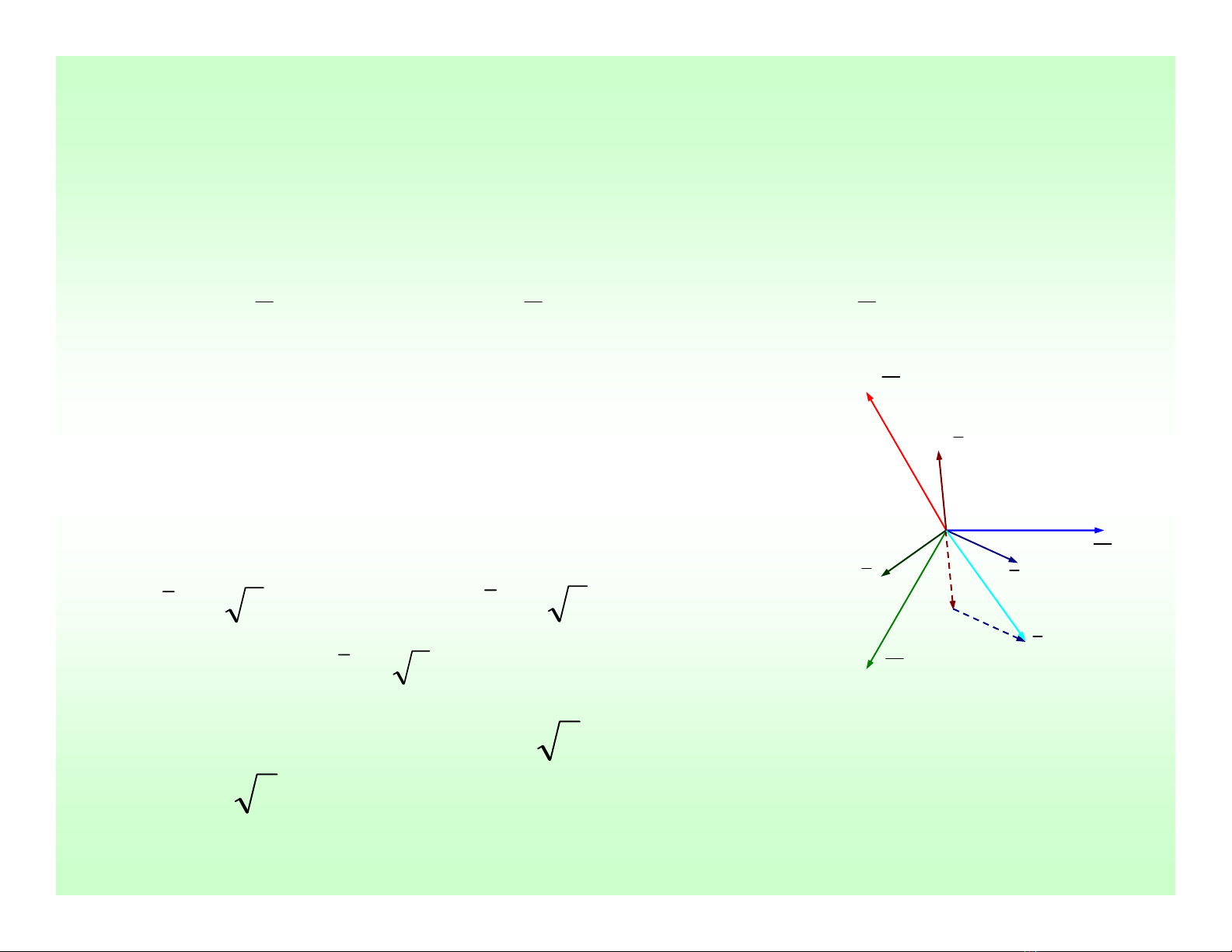
•Xét tiếptrường hợplưới điện xoay chiều ba pha cân bằng đấu Y-Δ:
0
0∠= Lab VV 0
120−∠= Lbc VV 0
120∠= Lca VV
ab
V
bc
V
ca
V
1
I
3
I
2
I
a
I
Ba dòng pha I1, I2, và I3chảy qua tải ba pha đấu
Δsẽcó góc lệch pha θso với áp dây tương ứng
với cùng giá trịdòng pha I
φ
. Từgiảnđồ vector
ta xác định được 3 dòng dây:
θ
φ
−−∠= 0
303IIa
θ
φ
−−∠= 0
1503IIb
θ
φ
−∠= 0
903IIc
¾Nhưvậyđấu Y-Y cho: và , đấuΔ-Δcho :
và
φ
VVL3=
φ
II L=
φ
VVL
=
φ
II L3=
HệThống Điện Xoay Chiều Ba Pha (tt)