Chương 6: ĐỒ THỊ(GRAPHIC)
Data structures and Algorithms
2/18/2021 Cấu trúc dữ liệu và giải thuật 1
Nội dung chính
•Các khái niệm cơ bản về đồ thị
•Cài đặt đồ thị
•Duyệt đồ thị
2/18/2021 Cấu trúc dữ liệu và giải thuật 2
Nội dung chính
•Các khái niệm cơ bản về đồ thị
•Cài đặt đồ thị
•Duyệt đồ thị
2/18/2021 Cấu trúc dữ liệu và giải thuật 3
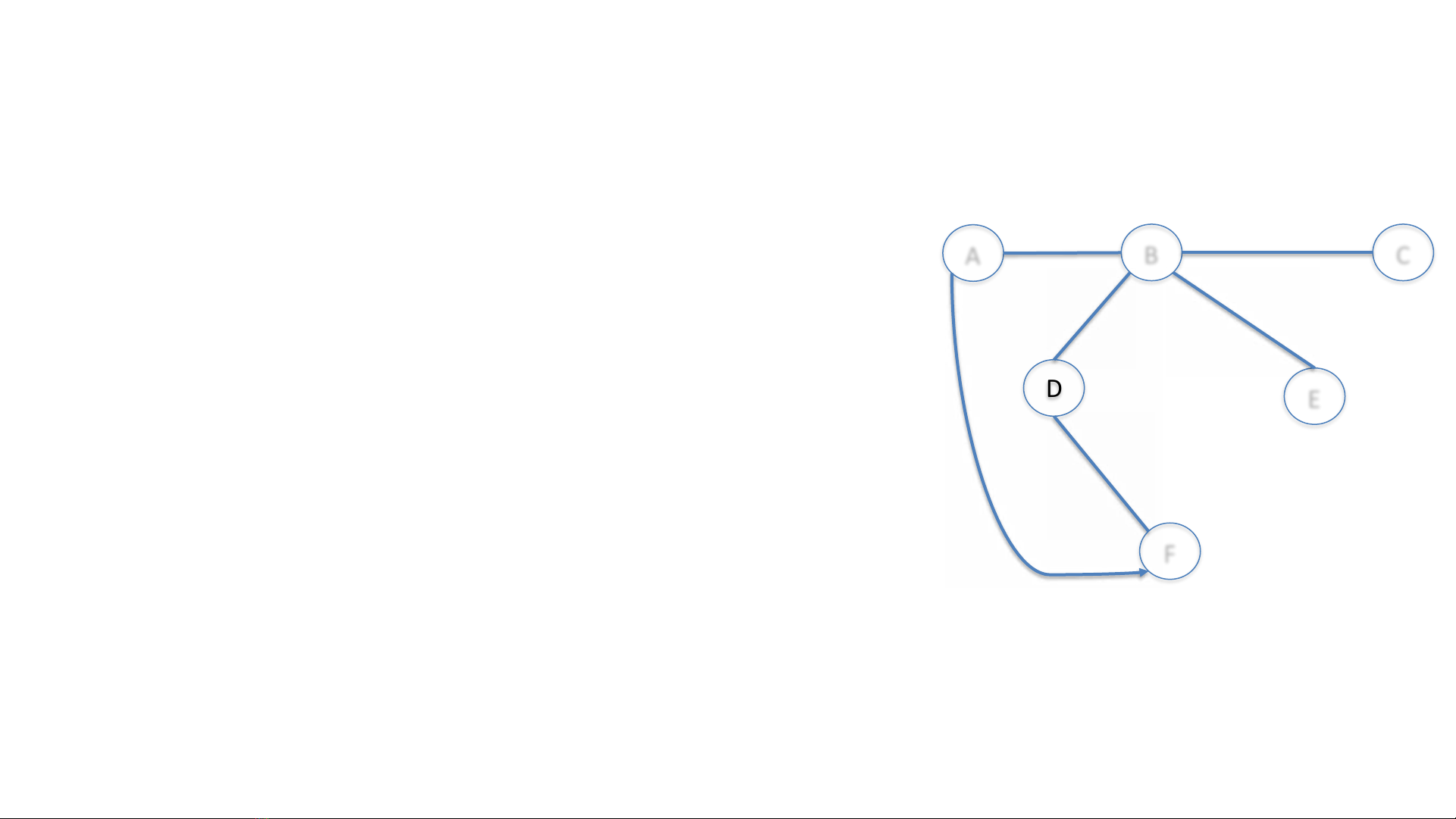
Các khái niệm cơ bản về đồ thị
Đồ thị G là một cấu trúc gồm hai thành phần:
▪𝑉 = {𝑣0, 𝑣1, … , 𝑣𝑚−1}: tập hữu hạn gồm 𝑚đỉnh
(nút, hay điểm).
▪𝐸 = {𝑒0, 𝑒1, … , 𝑒𝑛−1}, với 𝑒𝑖= (𝑣𝑗, 𝑣𝑘): tập hữu
hạn gồm 𝑛cạnh (hay cung) nối các cặp đỉnh.
Kí hiệu đồ thị G là G(V, E).
2/18/2021 Cấu trúc dữ liệu và giải thuật 4
B
AC
DE
F
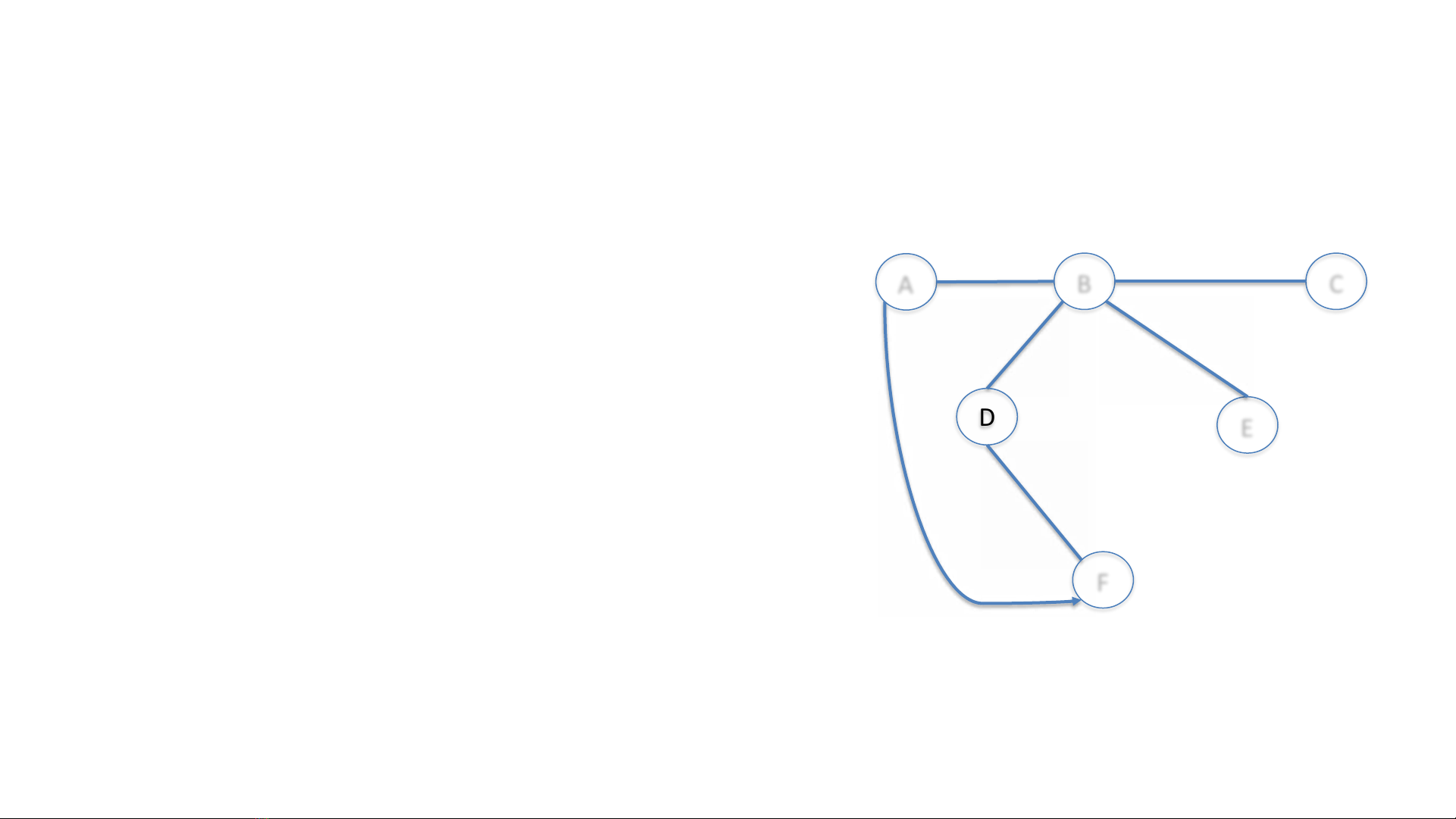
Các khái niệm cơ bản về đồ thị
Giả sử 𝑣𝑖là một đỉnh của đồ thị G(V,E).
Khi đó, ta gọi 𝑣𝑗là đỉnh kề của 𝑣𝑖
nếu (𝑣𝑖, 𝑣𝑗)
∈
E.
Đồng thời, bản thân (𝑣𝑖, 𝑣𝑗) cũng là cạnh
kề của 𝑣𝑖và 𝑣𝑗.
2/18/2021 Cấu trúc dữ liệu và giải thuật 5
B
AC
DE
F