1
1
CHƯƠNG 2: NGUYÊN LÝ II CỦA
NHIỆT ĐỘNG HỌC
2.1. Một số khái niệm
2.2. Nguyên lý II nhiệt động học
2.3. Tiên đề Planck về entropy tuyệt đối
2.4. Hàm đặc trưng và các phương trình nhiệt động
cơ bản
2.5. Ảnh hưởng của nhiệt độ đến thế đẳng áp
2.6. Ảnh hưởng của áp suất đến thế đẳng áp
2.7. Đại lượng mol riêng phần và thế hóa học
2
Quá trình tự diễn biến:là quá trình xảy ra không cần
tiêu tốn một công bên ngoài.
Đặc điểm:quá trình dần dần đạt tới cân bằng và phần
lớn có khả năng sinh công hữu ích.
Ví dụ:
+ Vật rơi từ cao xuống thấp.
+ Nước chảy từ cao xuống thấp.
+ Nhiệt truyền từ vật nóng sang vật lạnh.
+ Phản ứng hóa học xảy ra theo một chiều nhất định:
NaOH + HCl = NaCl + H2O
2.1.1. QUÁ TRÌNH TỰ DIỄN BIẾN (TỰ XẢY RA)
2.1 MỘT SỐ KHÁI NIỆM
3
Quá trình không tự diễn biến:là quá trình xảy ra dưới
tác dụng của một công bên ngoài.
Về nguyên tắc,chỉ có thể làm môt quá trình không tự
diễn biến xảy ra khi tiêu tốn năng lượng của một quá
trình tự diễn biến khác
Ví dụ:
+ Nâng một vật lên cao.
+ Bơm nước từ giếng lên.
+ Phản ứng ngược lại:
NaCl + H2O = NaOH + HCl
2.1.2. QUÁ TRÌNH KHÔNG TỰ DIỄN BIẾN
2.1 MỘT SỐ KHÁI NIỆM
4
Quá trình thuận nghịch:là quá trình mà khi
biến đổi hệ từ trạng thái cuối về trạng thái đầu,hệ
sẽ đi qua các trạng thái trung gian như khi nó đi từ
trạng thái đầu đến trạng thái cuối và không gây nên
một biến đổi gì trong hệ cũng như môi trường.
Quá trình bất thuận nghịch:là quá trình không
có những tính chất trên.
2.1.3. QUÁ TRÌNH THUẬN NGHỊCH &BẤT THUẬN NGHỊCH
2.1 MỘT SỐ KHÁI NIỆM
2
5
Công hệ sinh ra trong quá trình thuận nghịch là cực đại.
(Amax)
Công do hệ thực hiện được gồm hai phần:công hữu ích
(công có thể sử dụng được)và công chống lại áp suất ngoài
(công dãn nở).
A = A’ + P.V hay A = A’ + P.dV
Xét chiều giới hạn của các quá trình tự diễn biến trong hệ
không cô lập:
Nếu A’>0 : Quá trình tự xảy ra
Nếu A’=0 : Quá trình cân bằng
Nếu A’<0 : Quá trình không tự xảy ra
2.1.3. QUÁ TRÌNH THUẬN NGHỊCH &BẤT THUẬN NGHỊCH
2.1 MỘT SỐ KHÁI NIỆM
6
Có nhiều cách phát biểu:
Nhiệt không thể truyền tự vật lạnh sang vật
nóng.
Trong một quá trình nhiệt không thể biến
hoàn toàn thành công.
Không thể có động cơ vĩnh cữu loại 2 là động
cơ sinh công từ 1 nguồn nhiệt .
2.2.1. PHÁT BIỂU NGUYÊN LÝ II
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
7
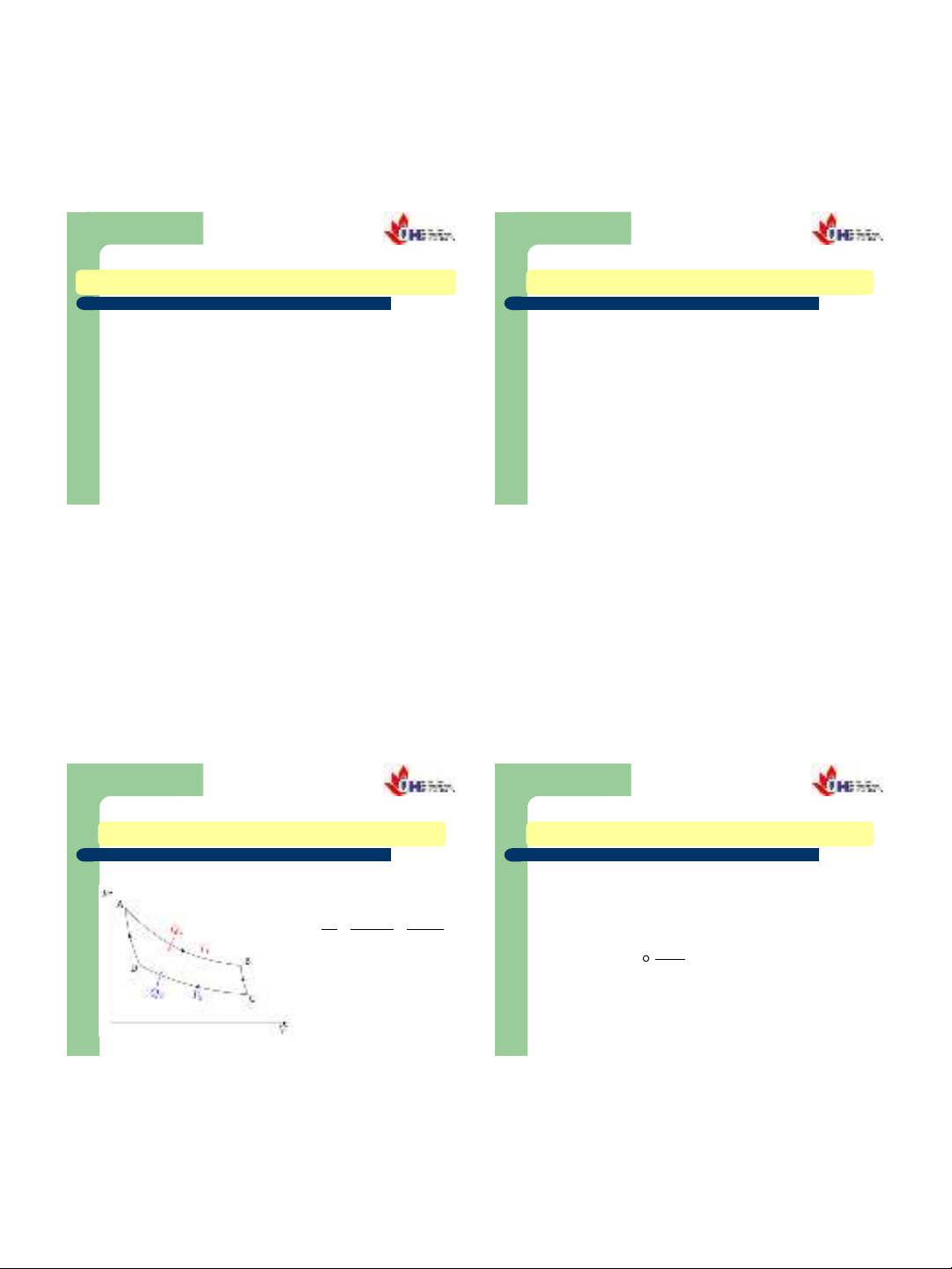
Chu trình thuận nghịch Carnot:
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.2. ENTROPY
Hiệu suất của mọi chu trình:
+Dấu “=”: chu trình thuận
nghịch.
+Dấu “<”: chu trình không
thuận nghịch.
1
21
1
21
1T
TT
Q
QQ
Q
A
η
8
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.2. ENTROPY
Biểu thức định lượng tổng quát của nguyên lý
hai cho mọi chu trình như sau: (Bất đẳng thức
Clausius)
+Dấu “=”: chu trình thuận nghịch.
+Dấu “<”: chu trình không thuận nghịch.
0
T
δQ
3
9
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.2. ENTROPY
Entropy: là đại lượng đặc trưng cho độ hỗn loạn của các
phần tử tạo thành hệ. Clausius đặt tên cho hàm đó là
entropy, ký hiệu là S: (đơn vị: Cal (J) / oK)
Tổng hợp cho hai quá trình thuận nghịch và bất thuận
nghịch ta có:
+Dấu “=”: chu trình thuận nghịch.
+Dấu “>”: chu trình không thuận nghịch.
(biểu thức toán học của nguyên lý II nhiệt động học)
TN
T
δQ
dS
T
δQ
dS
T
δQ
ΔS
10
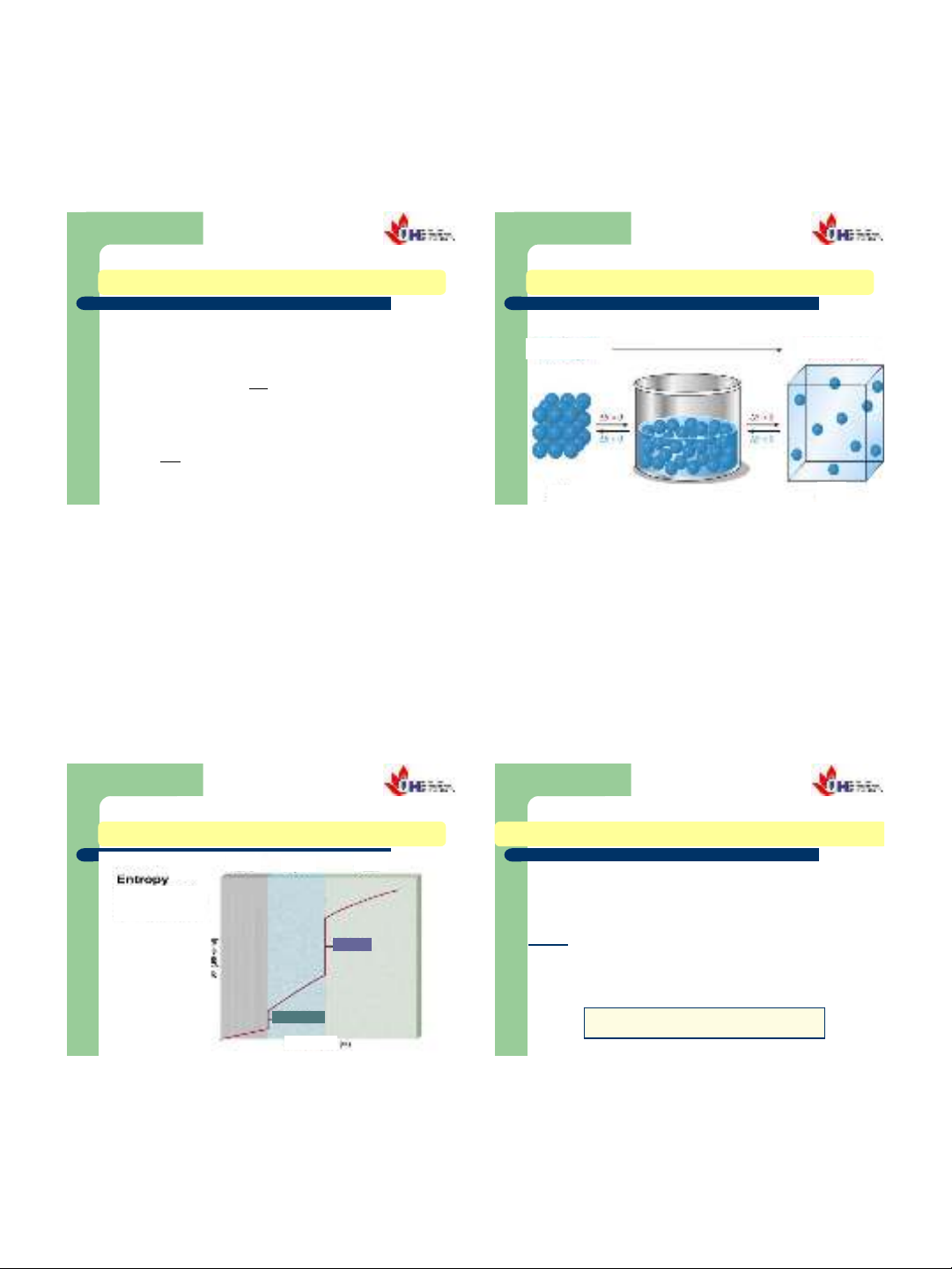
Tính hỗn loạnEntropy
Entropy
RắnLỏng Khí
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.2. ENTROPY
Sự biến thiên Entropy:
11
Rắn Lỏn
g
Khí
Sôi
Nóng
chảy
Nhiệt độ
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.2. ENTROPY
12
Nếu dS 0 (S tăng): Quá trình tự diễn biến.
Nếu dS = 0 hay d2S 0 (Smax): Quá trình đạt cân bằng.
Chú ý:ta có thể dùng S thay cho dS và nếu hệ không
cô lập ta có thể cô lập hệ bằng cách ghép thêm môi
trường vào hệ. Khi đó:
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.3. ENTROPY LÀ TIÊU CHUẨN XÉT CHIỀU TRONG HỆ CÔ LẬP
Scô lập = Shệ + Smôi trường

4
13
Entropy là thước đo độ trật tự của hệ.
Hệ cô lập: khi S > 0 thì quá trình tự xảy ra (theo chiều
tăng entropy), hệ đi từ trạng thái có độ trật tự lớn đến độ
trật tự nhỏ hay đến trang thái “hỗn loạn” hơn.
Hệ không cô lập:ta không dùng Sđể xét chiều tự xảy
ra của hệ mà ta chỉ nói rằng:
Nếu S > 0: Hệ đi đến trạng thái có độ trật tự nhỏ hơn.
Nếu S < 0: Hệ đi đến trạng thái có độ trật tự lớn hơn.
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.4. TÍNH CHẤT VÀ Ý NGHĨA VẬT LÝ CỦA ENTROPY
14
Tính chất của entropy:
Entropy là một hàm trạng thái của hệ,nó là đại lượng
dung độ nên có cộng tính,nghĩa là:
S = S1+ S2+…+ Sn=Si
Entropy là hàm của xác suất nhiệt động W: S = f(W)
Khi chuyển từ trạng thái 1 sang trạng thái 2thì:
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.4. TÍNH CHẤT VÀ Ý NGHĨA VẬT LÝ CỦA ENTROPY
1
2
12 ln W
W
kSSS
15
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.5. TÍNH TOÁN ENTROPY CỦA QUÁ TRÌNH THUẬN NGHỊCH
Biểu thức tổng quát cho quá trình thuận nghịch:
hay
Đơn vị của entropy là: J/.K hay cal/.K
TN
T
δQ
dS
2
21
1TN
Q
S S S T
16
Entropy của hệ chỉ phụ thuộc vào trạng thái đầu và trạng
thái cuối chứ không phụ thuộc vào đường đi của hệ.
ΔS = ΣSsản phẩm -ΣStác chất
Mỗi quá trình chuyển pha đều xảy ra ở một nhiệt độ xác
định (đẳng nhiệt). Biến thiên entropy ở nhiệt độ này là:
T
ΔH
ΔS cp
cp
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.5. TÍNH TOÁN ENTROPY CỦA QUÁ TRÌNH THUẬN NGHỊCH

5
17
Quá trình biến đổi đẳng tích:
Quá trình biến đổi đẳng áp:
Quá trình dãn nở đẳng nhiệt khí lý tưởng:
2
1
T
T
vT
dT
CS
2
1
T
T
PT
dT
CS
2
1
1
2
P
P
nRln
V
V
nRlnΔS
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.5. TÍNH TOÁN ENTROPY CỦA QUÁ TRÌNH THUẬN NGHỊCH
18
Ví dụ 1: Quá trình chuyển dạng thù hình từ Sthoi sang
Sđơn tà là thuận nghịch ở 95,40C. Nhiệt chuyển pha của S
ở nhiệt độ này là 0,72 kcal/mol. Xác định biến thiên
entropy của quá trình này :
Ví dụ 2: Tính Scủa quá trình giãn nở đẳng nhiệt thuận
nghịch 28g N2 khi áp suất tăng lên 10 lần:
2.2 NGUYÊN LÝ II NHIỆT ĐỘNG HỌC
2.2.5. TÍNH TOÁN ENTROPY CỦA QUÁ TRÌNH THUẬN NGHỊCH
1-
2
119167Cal.K
10
1
.ln
28
28
8,314.
P
P
nRlnΔS
1-1-
3
.KCal.Mol 1,95
95,4273
0,72.10
T
ΔH
ΔS
19
Năm 1912, Planck phát biểu:”Entropy của một chất rắn
nguyên chất có cấu tạo tinh thể hoàn chỉnh lý tưởng
ở00tuyệt đối bằng không”.
Từ đó có thể tính được biến thiên entropy tiêu chuẩn của
phản ứng hóa học bằng công thức
+ S0298 [Cal/Mol.K]: entropy tiêu chuẩn của các chất.
dau
0
298
cuoi
0
298
0
298 SSΔS
2.3 TIÊN ĐỀ PLANCK VỀ ENTROPY TUYỆT ĐỐI
0SlimST
0T
0
20
Hàm đặc trưng là một hàm trạng thái mà thông qua nó và
đạo hàm các cấp của nó có thể xác định mọi thông số vĩ mô
của hệ.
Các loại hàm đặc trưng: U, H, Svà 2thế sau:
Thế nhiệt động đẳng nhiệt,đẳng áp (hàm năng lượng
Gibbs): G = H –TS.Đơn vị: cal hoặc J.
Thế đẳng nhiệt,đẳng tích (thế đẳng tích hay hàm năng
lượng Helmholtz): F = U –TS.Đơn vị: cal hoặc J.
2.4 HÀM ĐẶC TRƯNG VÀ CÁC PHƯƠNG TRÌNH
NHIỆT ĐỘNG CƠ BẢN
2.4.1. ĐỊNH NGHĨA HÀM ĐẶC TRƯNG





![Bài giảng Truyền nhiệt [năm] chuẩn nhất](https://cdn.tailieu.vn/images/document/thumbnail/2017/20170821/kloiroong10/135x160/4471503277987.jpg)
![Bài giảng Khí lý tưởng Lê Quang Nguyên [PDF]](https://cdn.tailieu.vn/images/document/thumbnail/2016/20160115/doinhugiobay_11/135x160/3731452833386.jpg)



![Động lực học chất lỏng lý tưởng: Chương 4 [Chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2015/20150907/minhnhut1411995/135x160/1773168_156.jpg)
![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)














