http://lophocthem.com Phone: 01689.996.187 vuhoangbg@gmail.com
I. KIẾN THỨC
KHÚC XẠ ÁNH SÁNG
1. Hiện tượng khúc xạ ánh sáng
Hiện tượng khúc xạ ánh sáng là hiện tượng khi ánh sáng truyền qua mặt phân cách giữa hai
môi trường trong suốt, tia sáng bị bẻ gãy khúc (đổi hướng đột ngột) ở mặt phân cách.
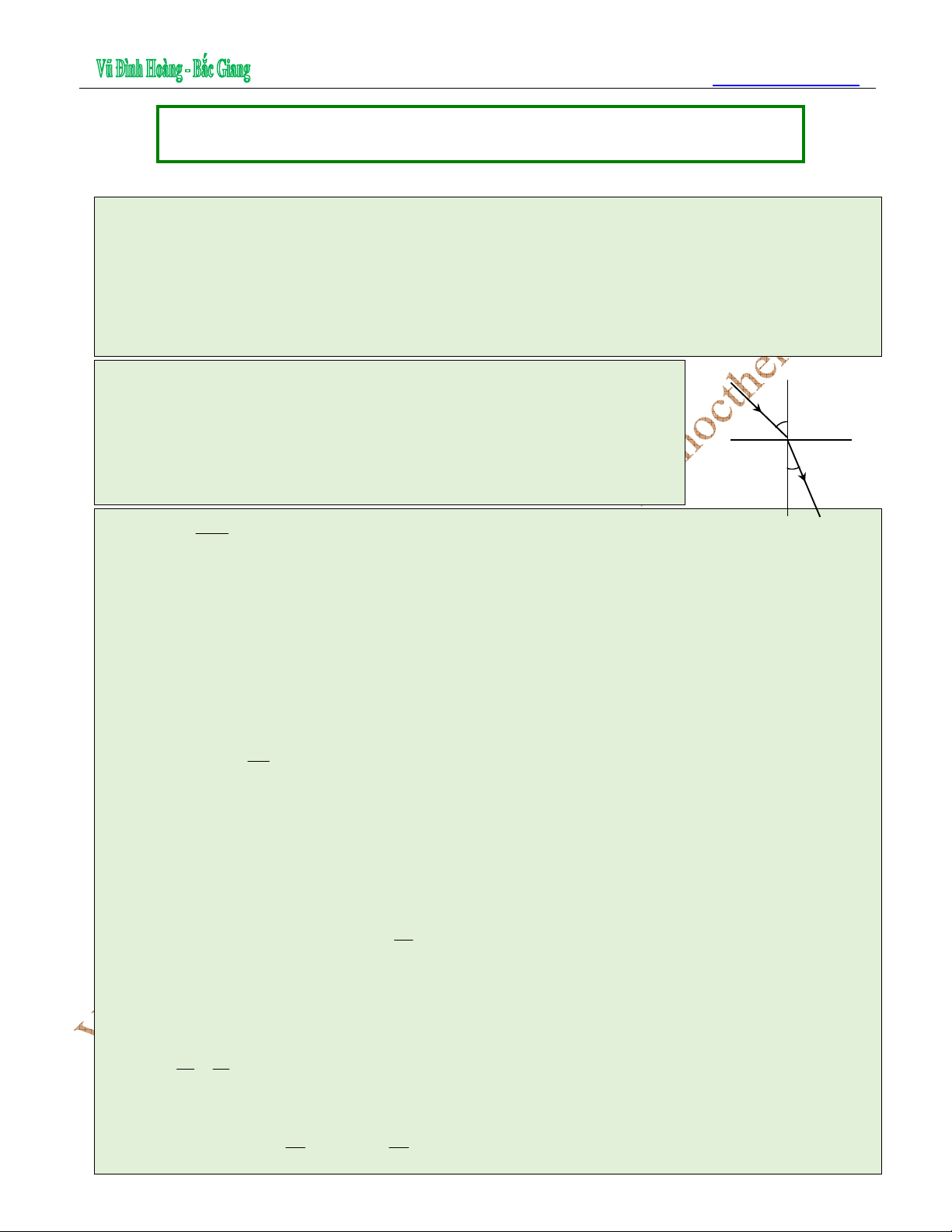
2. Định luật khúc xạ ánh sáng
+ Tia khúc xạ nằm trong mặt phẳng tới và ở bên kia pháp tuyến so với tia tới.
+ Đối với một cặp môi trường trong suốt nhất định thì tỉ số giữa sin
của góc tới (sini) với sin của góc khúc xạ (sinr) luôn luôn là một số
không đổi. Số không đổi này phụ thuộc vào bản chất của hai môi
trường và được gọi là chiết suất tỉ đối của môi trường chứa tia khúc
xạ (môi trường 2) đối với môi trường chứa tia tới (môi trường 1); kí
hiệu là n
21
.
Biểu thức:
21
sin
sin n
r
i=
+ Nếu n
21
> 1 thì góc khúc xạ nhỏ hơn góc tới. Ta nói môi trường (2)
chiết quang kém môi trường (1).
+ Nếu n
21
< 1 thì góc khúc xạ lớn hơn góc tới. Ta nói môi trường (2) chiết quang hơn môi
trường (1).
+ Nếu i = 0 thì r = 0: tia sáng chiếu vuông góc với mặt phân cách sẽ truyền thẳng.
+ Nếu chiếu tia tới theo hướng KI thì tia khúc xạ sẽ đi theo hướng IS (theo nguyên lí về tính
thuận nghịch của chiều truyền ánh sáng).
Do đó, ta có
12
21
1
n
n=
.
3. Chiết suất tuyệt đối
– Chiết suất tuyệt đối của một môi trường là chiết suất của nó đối với chân không.
– Vì chiết suất của không khí xấp xỉ bằng 1, nên khi không cần độ chính xác cao, ta có thể coi
chiết suất của một chất đối với không khí bằng chiết suất tuyệt đối của nó.
– Giữa chiết suất tỉ đối n
21
của môi trường 2 đối với môi trường 1 và các chiết suất tuyệt đối
n
2
và n
1
của chúng có hệ thức:
1
2
21
n
n
n=
– Ngoài ra, người ta đã chứng minh được rằng:
Chiết suất tuyệt đối của các môi trường trong suốt tỉ lệ nghịch với vận tốc truyền ánh sáng
trong các môi trường đó:
2
1
1
2
v
v
n
n=
Nếu môi trường 1 là chân không thì ta có: n
1
= 1 và v
1
= c = 3.10
8
m/s
Kết quả là:
2
n
=
2
v
c
hay v
2
=
2
n
c
.
CHUYÊN ĐỀ 6. KHÚC XẠ ÁNH SÁNG - PHẢN XẠ TOÀN PHẦN
i
r
N
N
/
I
S
K
(
1
(
2
http://lophocthem.com Phone: 01689.996.187 vuhoangbg@gmail.com
– Vì vận tốc truyền ánh sáng trong các môi trường đều nhỏ hơn vận tốc truyền ánh sáng trong
chân không, nên chiết suất tuyệt đối của các môi trường luôn luôn lớn hơn 1.
Ý nghĩa của chiết suất tuyệt đối
Chiết suất tuyệt đối của môi trường trong suốt cho biết vận tốc truyền ánh sáng trong môi
trường đó nhỏ hơn vận tốc truyền ánh sáng trong chân không bao nhiêu lần.
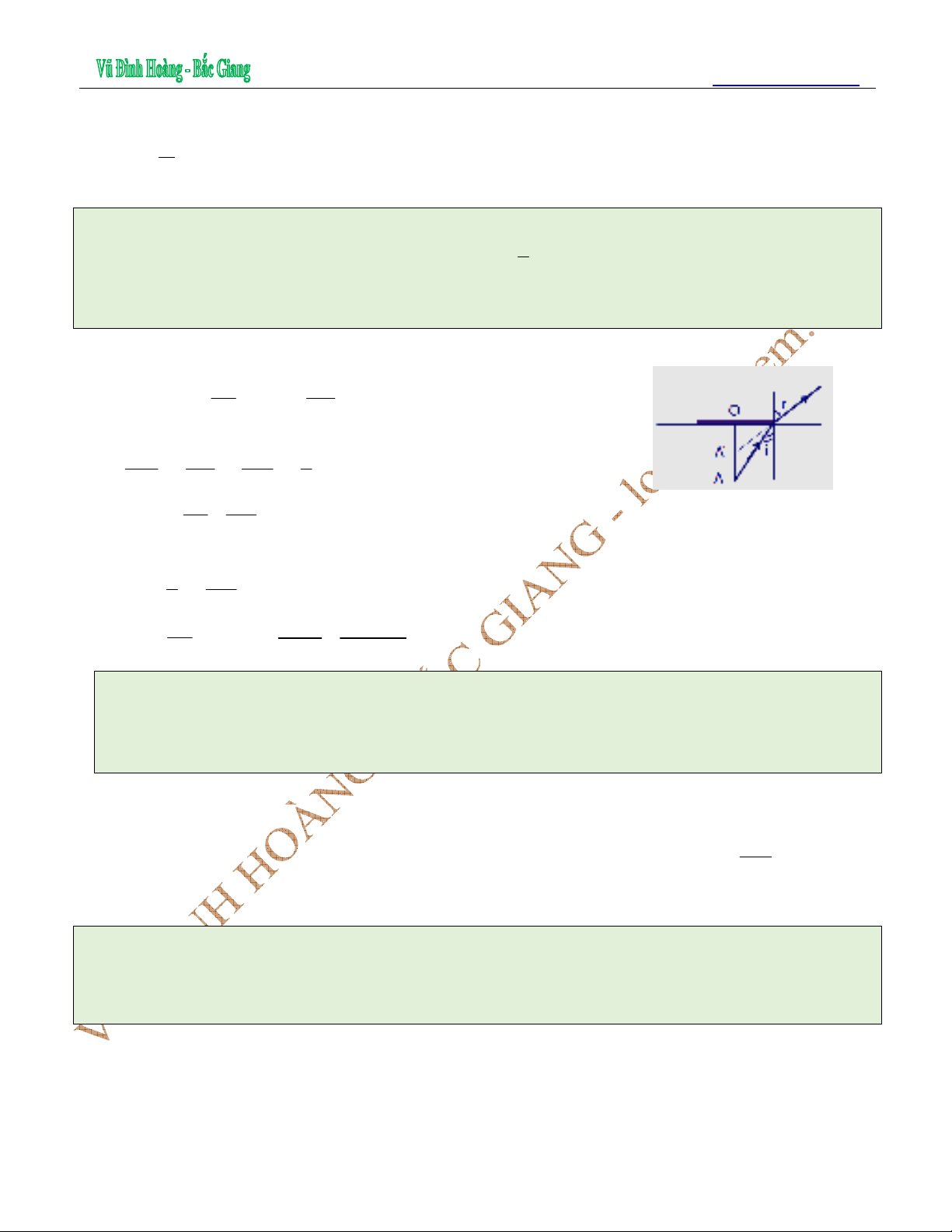
PHẢN XẠ TOÀN PHẦN
1. Hiện tượng phản xạ toàn phần
Hiện tượng phản xạ toàn phần là hiện tượng mà trong đó chỉ tồn tại tia phản xạ mà không có
tia khúc xạ.
+ Phản xạ toàn phần là hiện tượng phản xạ toàn bộ ánh sáng tới, xảy ra ở mặt phân cách giữa
hai môi trường trong suốt.
2. Điều kiện để có hiện tượng phản xạ toàn phần
– Tia sáng truyền theo chiều từ môi trường có chiết suất lớn sang môi trường có chiết suất
nhỏ hơn.
– Góc tới lớn hơn hoặc bằng góc giới hạn phản xạ toàn phần (i
gh
).
+ Điều kiện để có phản xạ toàn phần: Ánh sáng phải truyền từ môi trường chiết quang hơn
sang môi trường chiết quang kém (n
2
< n
1
) và góc tới i ≥ i
gh
.
+ Góc giới hạn phản xạ toàn phần: sini
gh
=
1
2
n
n
; với n
2
< n
1
.
3. Phân biệt phản xạ toàn phần và phản xạ thông thường
Giống nhau
– Cũng là hiện tượng phản xạ, (tia sáng bị hắt lại môi trường cũ).
– Cũng tuân theo định luật phản xạ ánh sáng .
Khác nhau
– Hiện tượng phản xạ thông thường xảy ra khi tia sáng gặp một mặt phân cách hai môi trường
và không cần thêm điều kiện gì.
Trong khi đó, hiện tượng phản xạ toàn phần chỉ xảy ra khi thỏa mãn hai điều kiện trên.
– Trong phản xạ toàn phần, cường độ chùm tia phản xạ bằng cường độ chùm tia tới. Còn
trong phản xạ thông thường, cường độ chùm tia phản xạ yếu hơn chùm tia tới.
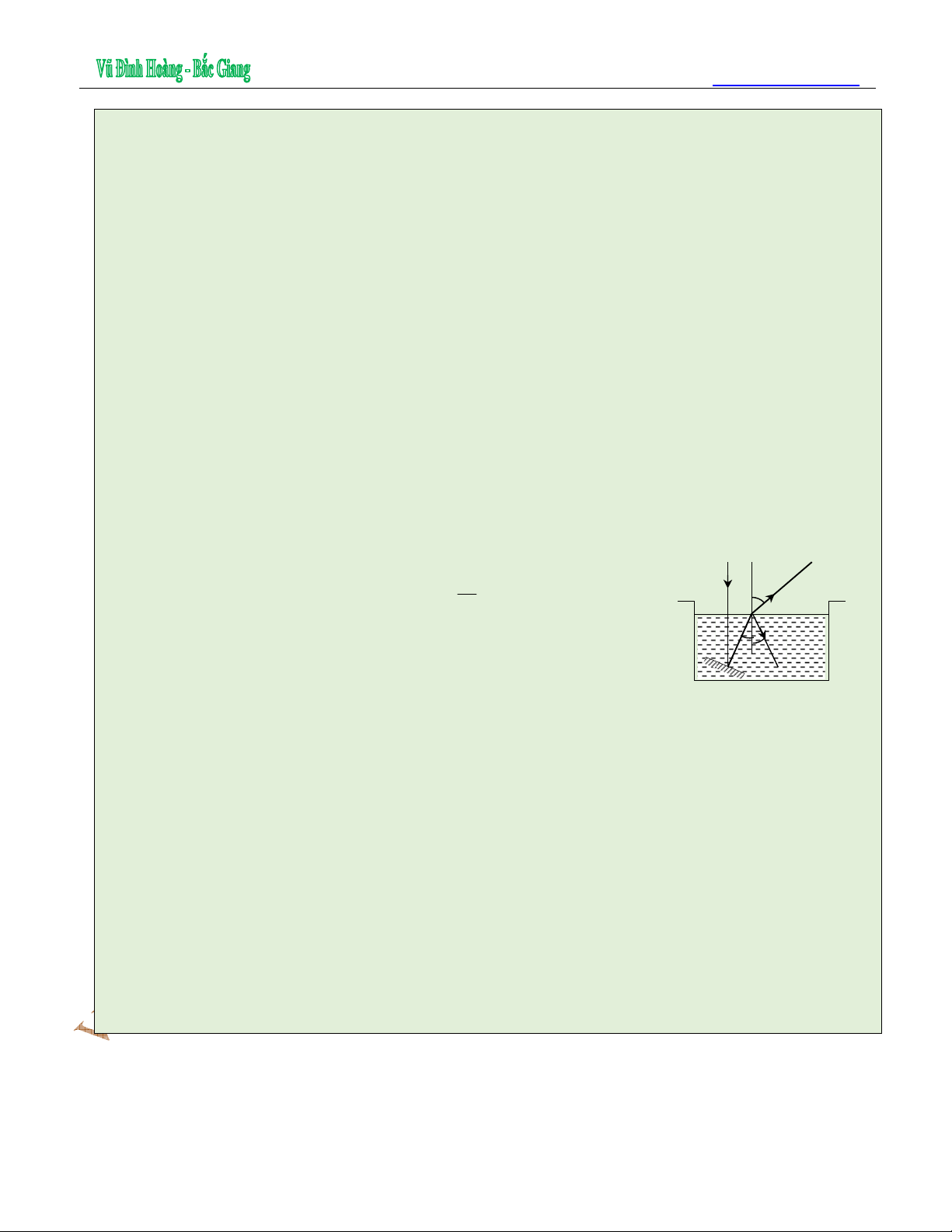
4. Lăng kính phản xạ toàn phần
Lăng kính phản xạ toàn phần là một khối thủy tinh hình lăng trụ có tiết diện thẳng là một tam
giác vuông cân
Ứng dụng
Lăng kính phản xạ toàn phần được dùng thay gương phẳng trong một số dụng cụ quang học
(như ống nhòm, kính tiềm vọng …) Sợi cáp quang.
G
S
R
K
I
J
i
i
/
r
H
http://lophocthem.com Phone: 01689.996.187 vuhoangbg@gmail.com
VÍ DỤ MINH HỌA
VD1. Tia sáng đi từ nước có chiết suất n
1
=
3
4
sang thủy tinh có chiết suất n
2
= 1,5. Tính góc
khúc xạ và góc lệch D tạo bởi tia khúc xạ và tia tới, biết góc tới i = 30
0
.
HD. Ta có:
1
2
sin
sin
n
n
r
i= sinr =
2
1
n
nsini = sin26,4
0
r = 26,4
0
;
D = i – r = 3,6
0
.
VD2. Tia sáng truyền trong không khí tới gặp mặt thoáng của chất lỏng có chiết suất n =
3
. Ta
được hai tia phản xạ và khúc xạ vuông góc với nhau. Tính góc tới.
HD. Ta có:
r
i
sin
sin
= n; vì i’ + r = i + r =
2
π
sinr = sin(- i) = cosi
r
i
sin
sin =
i
i
cos
sin = tani = n = tan
3
π
i =
3
π
.
VD3. Một cây cọc dài được cắm thẳng đứng xuống một bể nước chiết suất n =
3
4
. Phần cọc nhô
ra ngoài mặt nước là 30 cm, bóng của nó trên mặt nước dài 40 cm và dưới đáy bể nước dài 190
cm. Tính chiều sâu của lớp nước.
HD. Ta có: tani =
30
40
=
AB
BI
= tan53
0
i = 53
0
;
r
i
sin
sin
= n sinr =
n
isin
= 0,6 = sin37
0
r = 37
0
; tanr =
IH
CHCD
IH
HD
−
=
IH =
r
CHCD
tan
−
=
75,0
40190
−
= 200 (cm).
VD4. Một cái máng nước sâu 30 cm rộng 40 cm có hai thành bên thẳng đứng. Lúc máng cạn
nước thì bóng râm của thành A kéo dài tới đúng chân thành B đối diện. Người ta đổ nước vào
máng đến một độ cao h thì bóng của thành A ngắn bớt đi 7 cm so với trước. Biết chiết suất của
nước là n =
3
4
. Tính h.
HD. Ta có: tani =
3
4
30
40' ===
AC
CB
AA
CI
= tan53
0
i = 53
0
;
r
i
sin
sin
= n sinr =
n
isin
= 0,6 = sin37
0
r = 37
0
; tani =
h
BI '
; tanr =
h
BI
h
DBBI 7''
−
=
−
7
'
'
tan
tan
−
=
B
I
BI
r
i
=
9
16
I’B = 16 (cm); h =
i
BI
tan
'
= 12 (cm).
VD5.Một người ngồi trên bờ nhúng chân vào nước trong suốt. Biết chiết suất nước là n =
3
4
.
a) Khoảng cách thực từ bàn chân người đó đến mặt nước là 36 cm. Hỏi mắt người đó cảm
thấy bàn chân cách mặt nước bao nhiêu?

http://lophocthem.com Phone: 01689.996.187 vuhoangbg@gmail.com
b) Người này cao 1,68 m, nhìn thấy một hòn sỏi dưới đáy hồ dường như cách mặt nước 1,5 m.
Hỏi nếu đứng dưới hồ thì người ấy có bị ngập đầu không?.
HD.
a) Ta có:
2
1
'n
n
d
d=
d’ =
1
2
n
n
d = 27 cm.
b) Ta có:
2
1
'n
n
h
h=
h =
2
1
n
n
h’ = 2 m > 1,68 m nên nếu đứng dưới hồ thì người đó sẻ bị ngập đầu.
VD6. Tính vận tốc của ánh sáng trong thủy tinh. Biết thủy tinh có chiết suất n = 1,6 và vận tốc
ánh sáng trong chân không là c = 3.10
8
m/s.
Ta có: n =
v
c
v =
n
c
= 1,875.10
8
m/s.
VD7. Tính vận tốc của ánh sáng truyền trong môi trường nước. Biết tia sáng truyền từ không
khí với góc tới là i = 60
0
thì góc khúc xạ trong nước là r = 40
0
. Lấy vận tốc ánh sáng ngoài
không khí c = 3.10
8
m/s.
HD.
Ta có: v =
n
c
và n =
r
i
sin
sin
v =
i
rc
sin
sin.
= 2,227.10
8
m/s.
VD8. Tính góc giới hạn phản xạ toàn phần khi ánh sáng truyền từ thủy tinh sang không khí, từ
nước sang không khí và từ thủy tinh sang nước. Biết chiết suất của thủy tinh là 1,5; của nước là
3
4
.
HD. Ta có sini
gh
=
1
2
n
n
= sin53
0
i
gh
= 53
0
.
VD9. Thả nổi trên mặt nước một đĩa nhẹ, chắn sáng, hình tròn. Mắt người quan sát đặt trên mặt
nước sẽ không thấy được vật sáng ở đáy chậu khi bán kính đĩa không nhỏ hơn 20 cm. Tính
chiều sâu của lớp nước trong chậu. Biết rằng vật và tâm đĩa nằm trên đường thẳng đứng và chiết
suất của nước là n =
3
4
.
HD. Ta có: Sini
gh
=
n
1=
22
hR
R
+
h = R
1
2
−n
= 17,64 cm.
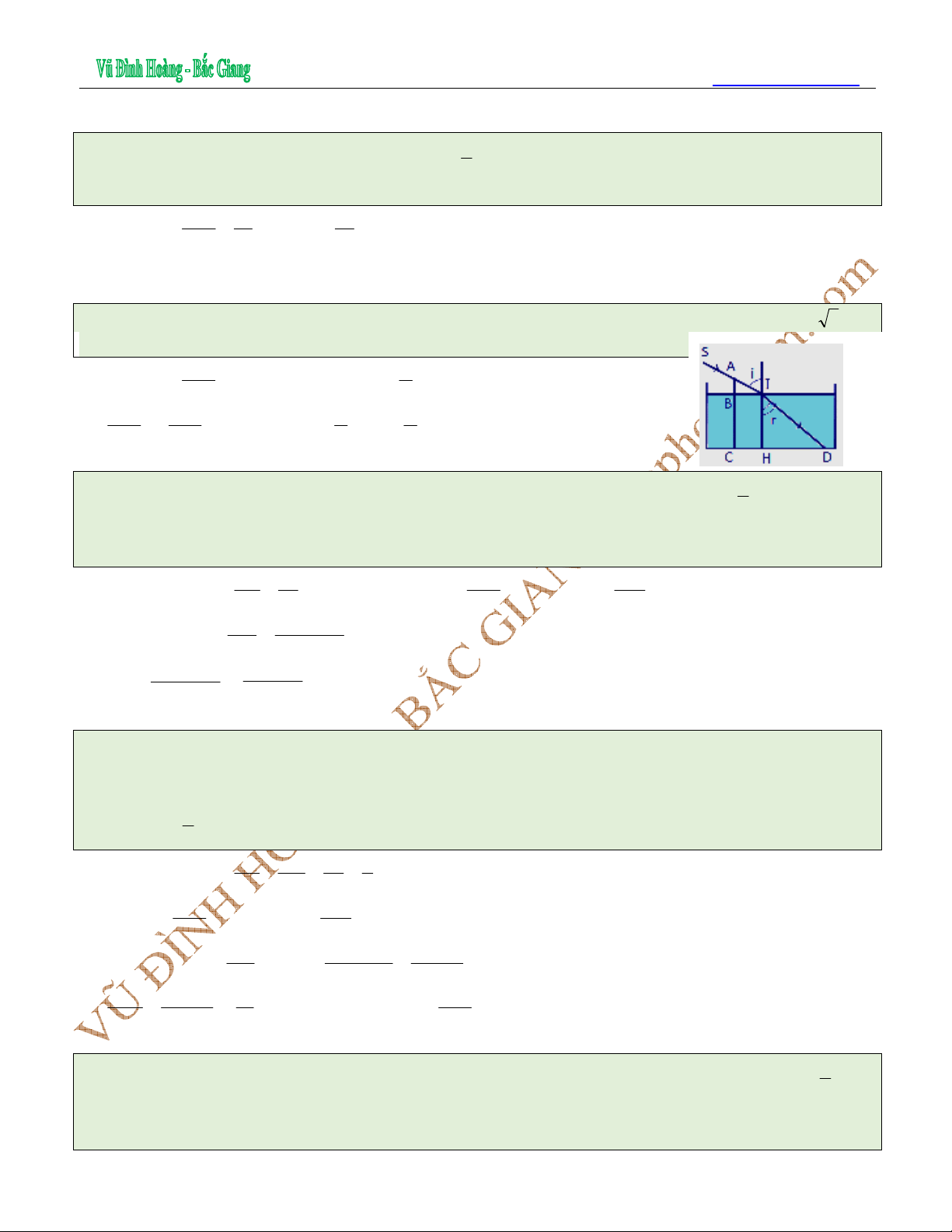
VD10. Một tấm thủy tinh mỏng, trong suốt, chiết suất n
1
= 1,5; có tiết diện là hình chử nhật
ABCD (AB rất lớn so với AD), mặt đáy AB tiếp xúc với một chất lỏng có chiết suất n
2
=
2
.
Chiếu tia sáng SI nằm trong mặt phẵng ABCD tới mặt AD sao cho tia tới nằm phía trên pháp
tuyến ở điểm tới và tia khúc xạ trong thủy tinh gặp đáy AB ở điểm K. Tính
giá trị lớn nhất của góc tới i để có phản xạ toàn phần tại K.
HD.
Để có phản xạ toàn phần tại K thì sini
1
≥ sini
gh
=
1
2
n
n
= sin70,5
0
http://lophocthem.com Phone: 01689.996.187 vuhoangbg@gmail.com
i
1
≥ 70,5
0
r ≤ 90
0
– 70,5
0
= 19,5
0
sini ≤
1
1
n
cosr = sin39
0
i ≤ 39
0
.
VD11. Một miếng gỗ mỏng, hình tròn bán kính 4 cm. Ở tâm O cắm thẳng góc một cái đinh OA.
Thả miếng gỗ trong một chậu nước có chiết suất n =
3
4
cho đầu A quay xuống đáy chậu.
a) Cho OA = 6 cm. Mắt đặt trong không khí sẽ thấy đầu A cách mặt nước bao nhiêu ?
b) Tìm chiều dài lớn nhất của OA để mắt không nhìn thấy đầu A của đinh.
HD.
a) Mắt đặt trong không khí sẽ thấy ảnh A’ của A.
Ta có: tani =
OI
OA
; tanr =
'
OI
OA
.
Với i và r nhỏ thì tani ≈ sini; tanr ≈ sinr
tan
t anr
i
=
'
OA
OA
≈
sin
sinr
i
=
1
n
OA’ =
6
1,33
OA
n
=
= 4,5 (cm).
b) Khi i ≥ i
gh
thì không thấy đầu A của đinh.
sini
gh
=
1
n
=
1
1,33
= sin48,6
0
i
gh
= 48,6
0
;
tani
gh
=
OI
OA
OA =
0
4
tan tan 48,6
gh
OI
i
= = 3,5 (cm).
VD12. Một bể chứa nước có thành cao 80 (cm) và đáy phẳng dài 120 (cm) và độ cao mực
nước trong bể là 60 (cm), chiết suất của nước là 4/3. Ánh nắng chiếu theo phương nghiêng
góc 30
0
so với phương ngang. Độ dài bóng đen tạo thành trên đáy bể là:
A. 11,5 (cm) B. 34,6 (cm) C. 51,6 (cm) D. 85,9 (cm)
HD.
- Độ dài phần bóng đen trên mặt nước là a = 34,6 (cm).
- Độ dài phần bóng đen trên đáy bể là b = 34,6 + 60.tanr trong đó r được tính
n
r
sin
isin =
suy ra b
= 85,9 (cm).
VD13. Một miếng gỗ hình tròn, bán kính 4 (cm). Ở tâm O, cắm thẳng góc một đinh OA. Thả
miếng gỗ nổi trong một chậu nước có chiết suất n = 1,33. Đinh OA ở trong nước, cho OA = 6
(cm). Mắt đặt trong không khí, chiều dài lớn nhất của OA để mắt không thấy đầu A là:
A. OA = 3,25 (cm). B. OA = 3,53 (cm). C. OA = 4,54 (cm). D. OA = 5,37 (cm).


























