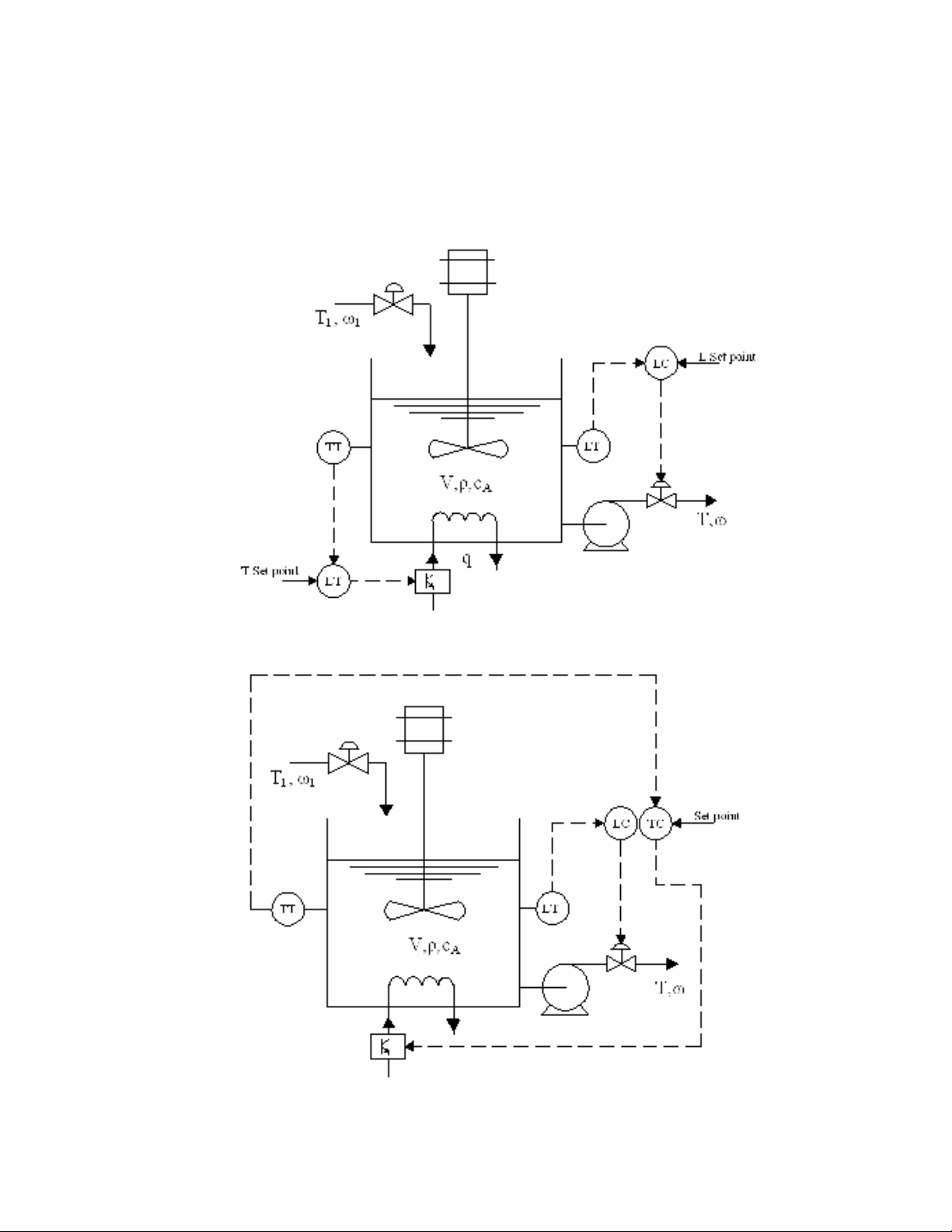
- Sử dụng hai bộ điều khiển riêng biệt để điều khiển nhiệt độ và mức nước
nhằm duy trì hệ thống làm việc ổn định tại giá trị đặt.
- Sử dụng một bộ điều khiển đa chức năng thực hiện cả hai chức năng điều
khiển nhiệt độ và mức nước.
Sơ đồ sử dụng hai bộ điều khiển độc lập để điều khiển nhiệt độ và mức
Sơ đồ sử dụng một bộ điều khiển đa chức năng để điều khiển nhiệt độ và mức
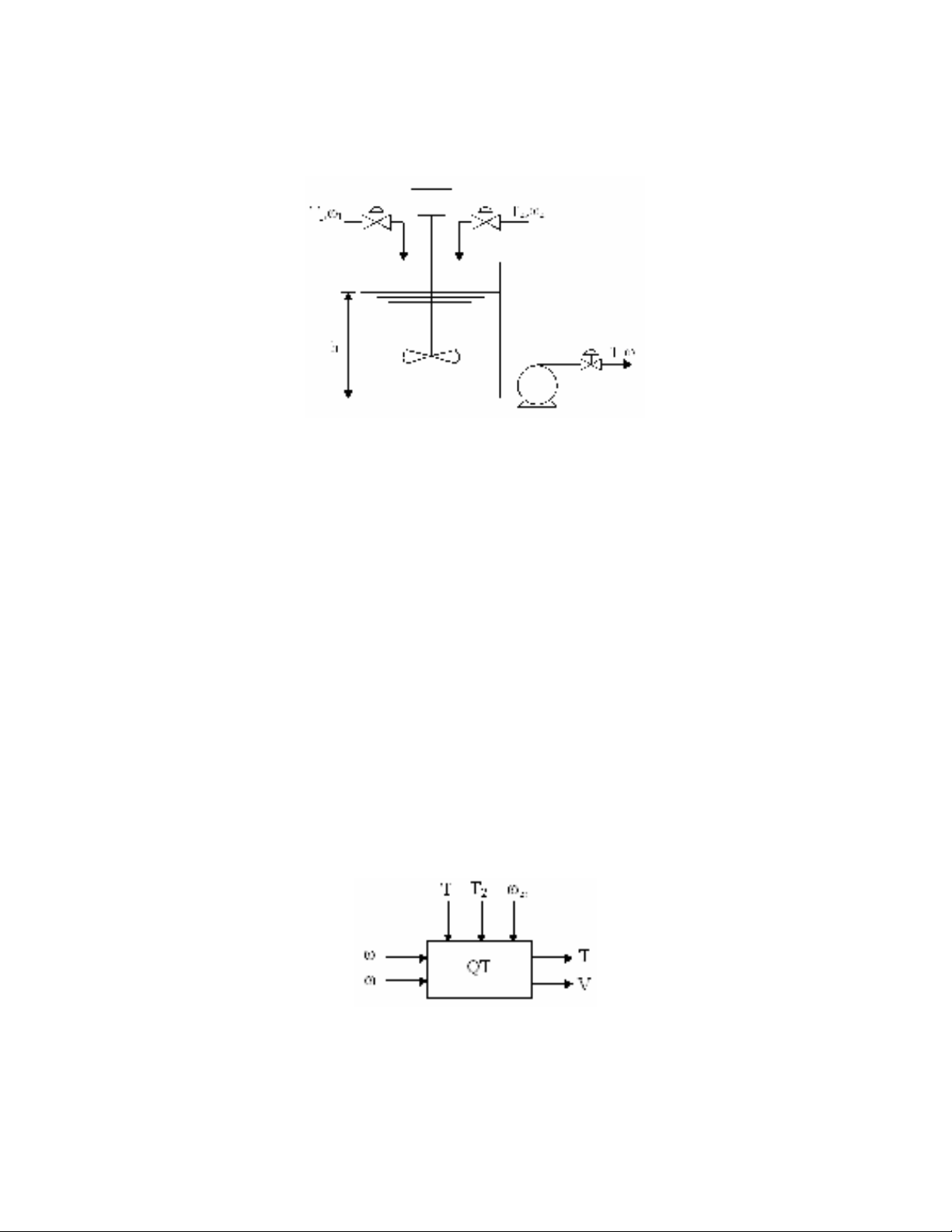
Bài 3.4.a)
a) Phân tích hệ thống
Bài toán là một quá pha trộn hai công chất lỏng nhằm duy trì nhiệt độ T và thể tích
bình V ở một giá trị không đổi. Như trên hệ thống ta thấy quá trình có các biến T1, ω1, T2,
ω2, T, ω. Nhiệt độ T1, T2 thường khó có thể can thiệp nên ta không dùng nó để điều khiển
nhiệt độ trong bình mà chỉ coi là nhiễu của quá trình. Để gia nhiệt hệ thống thì ta cần thay
đổi lưu lượng dòng công chất cung cấp vào hệ thống, với bài toán này tuỳ theo yêu cầu
thực tế mà ta có thể chọn một trong hai biến ω1, ω2 hoặc cả hai để điều khiển nhiệt độ
trong bình. Ở đây ta chọn ω1 làm biến điều khiển còn ω2 ta coi là một nhiễu. Như vậy thể
tích trong bình chỉ còn có thể điều khiển được bằng lưu lượng ωĐể đơn giản hoá bài toán
ta đưa ra một số giả thiết sau đây:
- Khối lượng riêng chất lỏng cấp vào trong bình và khối lượng riêng chất
lỏng trong bình là như nhau và là hằng số của quá trình ρ1 = ρ2 = ρ = const.
- Nhiệt độ của bình trao đổi với môi trường xung quanh là không đáng kể.
- Bình được trang bị thiết bị khuấy trộn lý tưởng, nhiệt độ tại mọi điểm trong
bình là như nhau.
b) Phương trình vi phân biểu diễn hệ thống.
Theo định luật bảo toàn khối lượng toàn phần ta có:
21
dt
)V(d (10)
Theo định luật bảo toàn năng lượng ta có:
hhh
dt
dh
V
dt
dV
h
hhh
dt
)Vh(d
2211
2211
(11)
Thay phương trình (10) vào (11) ta được:
)hh()hh(
dt
dh
V
hhh
dt
dh
V)(h
2211
221121
c) Phân tích bậc tự do của hệ thống.
Ta thấy hệ thống có 7 biến quá trình T, T1, T2, ω, ω1, ω2, V và 2 phương trình vi
phân. Như vậy số bậc tự do của hệ thống là 7 – 2 = 5, đúng bằng số biến vào. Điều này
cho biết mô hình ta đã xây dựng được là chính xác.
Hệ thống có 5 bậc tự do nghĩa là ta có thể xây dựng được 5 vòng điều khiển độc lập
cho 5 biến vào. Tuy nhiên để điều khiển hệ thống ta chỉ cần xây dựng hai vòng điều
khiển cho hai biến điều khiển là ω và ω1 là đủ.
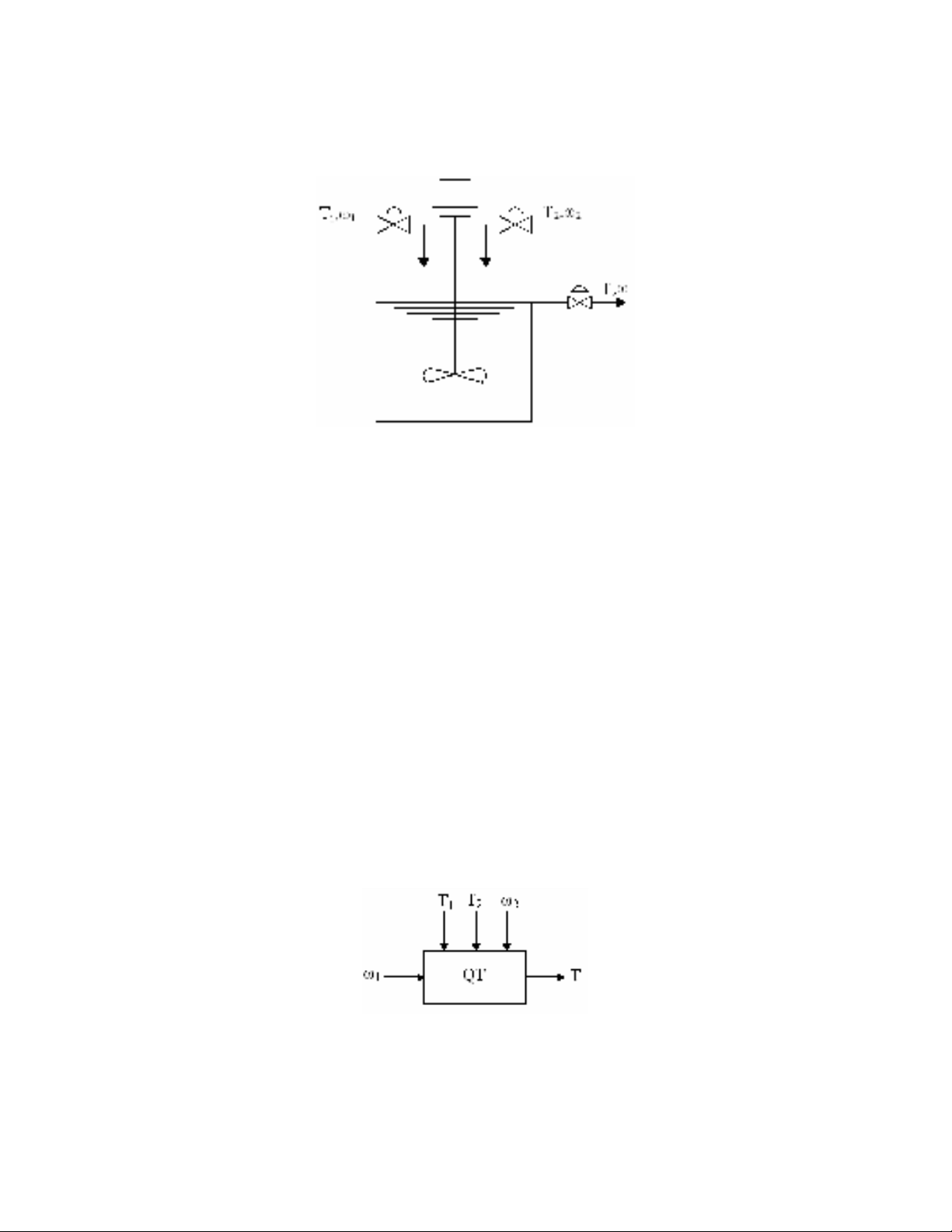
Bài 3.4.b)
a) Phân tích hệ thống
Bài toán là một quá pha trộn hai công chất lỏng nhằm duy trì nhiệt độ T ở một giá
trị không đổi. Ta thấy quá trình có các biến T1, ω1, T2, ω2, T, ω = ω1 + ω2. Nhiệt độ T1, T2
thường khó có thể can thiệp nên ta không dùng nó để điều khiển nhiệt độ trong bình mà
chỉ coi là nhiễu của quá trình. Để gia nhiệt hệ thống thì ta cần thay đổi lưu lượng dòng
công chất cung cấp vào hệ thống, với bài toán này tuỳ theo yêu cầu thực tế mà ta có thể
chọn một trong hai biến ω1, ω2 hoặc cả hai để điều khiển nhiệt độ trong bình. Ở đây ta
chọn ω1 làm biến điều khiển còn ω2 ta coi là một nhiễu. Bình trong hệ thống là bình tràn
nên có V = const và ω = ω1 + ω2 tại mọi thời điểm. Để đơn giản hoá bài toán ta đưa ra
một số giả thiết sau đây:
- Khối lượng riêng chất lỏng cấp vào trong bình và khối lượng riêng chất
lỏng trong bình là như nhau và là hằng số của quá trình ρ1 = ρ2 = ρ = const.
- Nhiệt độ của bình trao đổi với môi trường xung quanh là không đáng kể.
- Bình được trang bị thiết bị khuấy trộn lý tưởng, nhiệt độ tại mọi điểm trong
bình là như nhau.
b) Phương trình vi phân biểu diễn hệ thống.
Theo định luật bảo toàn năng lượng ta có:
h)(hh
dt
dh
V
hhh
dt
)Vh(d
212211
2211
với h, h1, h2 là enthanpy của bình chứa và dòng vào 1, dòng vào 2. Thay h = CT và
coi nhiệt dung riêng của dòng vào và của chất lỏng trong bình là như nhau C = C1 =C2 ta
được:
T)(TT
dt
dT
V212211
c) Phân tích bậc tự do của hệ thống.
Ta thấy hệ thống có 5 biến quá trình T, T1, T2, ω1, ω2 và 1 phương trình vi phân.
Như vậy số bậc tự do của hệ thống là 5 – 1 = 4, đúng bằng số biến vào. Điều này cho biết
mô hình ta đã xây dựng được là chính xác.
Hệ thống có 4 bậc tự do nghĩa là ta có thể xây dựng được 4 vòng điều khiển độc lập
cho 4 biến vào. Ta chọn ω1 là biến điều khiển vì thế ta chỉ cần xây dựng vòng điều khiển
cho 1 biến quá trình này.
d) Tuyến tính hoá phương trình.
Tại có phương trình làm việc tại điểm cân bằng
0T)(TT
dt
Td
V212211
phương trình cho thấy biến điều khiển T là phi tuyến với ω. Vì thế để chuyển sang
được mô hình hàm truyền đạt ta cần tuyến tính hoá phương trình này.
)T,T,,T,(fT)(TT
dt
dT
V2211212211
Đặt y = ∆T, d1 = ∆T1, d2 = ∆T2, d3 = ∆ω2, u = ∆ω1. Phương trình (5) viết lại được:
1
1
3
2
2
2
1
1
2211 u
d
df
d
d
df
d
dT
df
d
dT
df
y
dT
df
)T,T,,T,(f
dt
dy
V
)s(u
Vs
TT
d
Vs
TT
)s(
2
d
Vs
)s(d
Vs
)s(y
)s(u)TT()s(d).TT()s(d.)s(d)s(y)Vs(
u)TT(d).TT(d.dy).(0
dt
dy
V
1
21
1
3
21
2
21
2
.1
21
1
113222.1121
113222.1121