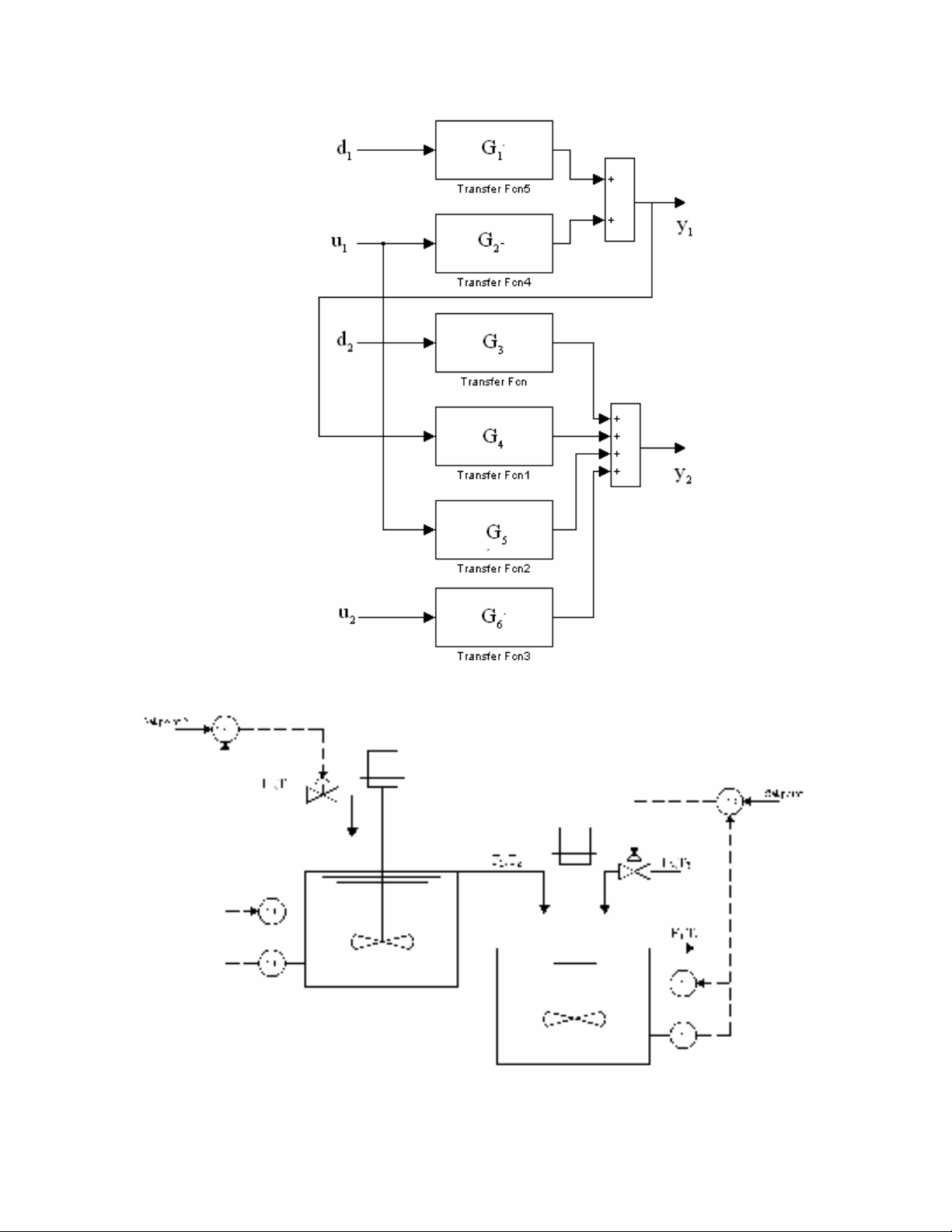
f) Lưu đồ P&ID
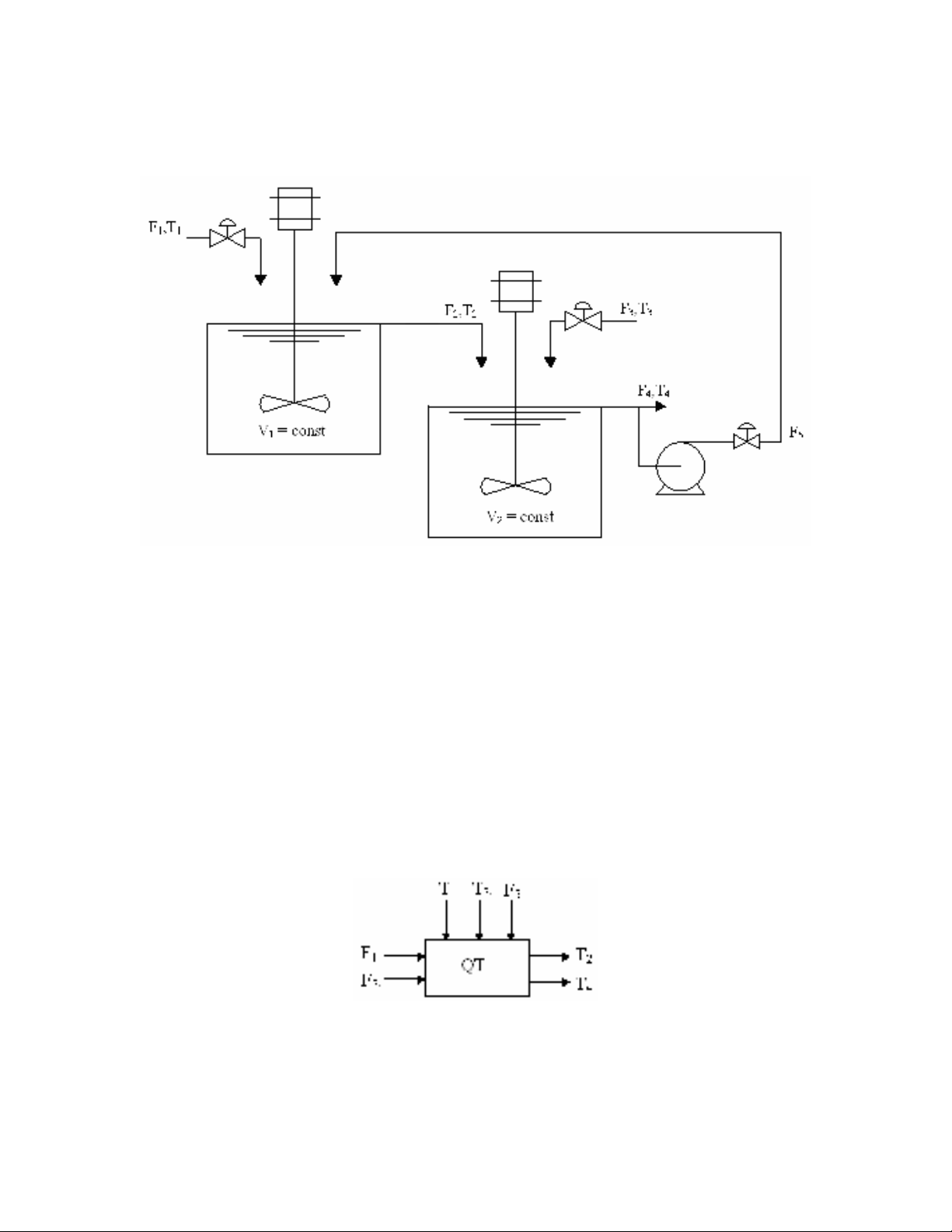
Bài 3.8
a) Phân tích bài toán
hệ thống gồm 2 bình chứa với mục đích ổn định nhiệt độ T2, T4. Bình chứa của hệ
thống là bình tràn nên V1 = const, V2 = const. Dựa vào sơ đồ ta thấy biến vào điều khiển
cho nhiệt đô T2 chính là lưu lượng vào F1, biến điều khiển cho nhiệt độ T4 là lưu lượng
vào F3. Do V1 = const, V2 = const nên F2 = F1+F5, F4 = F1 + F3 . Đối với bình 1 thì F1 là
biến vào điều khiển, T1, F5 là nhiễu. Còn với bình 2 thì F1, F5, T5 là nhiễu của quá trình,
T3 là biến điều khiển. Để đơn giản bài toán ta đưa ra một số giả thiết sau đây:
- Khối lượng riêng chất lỏng cấp vào trong bình và khối lượng riêng chất lỏng
trong bình là như nhau và là hằng số của quá trình ρ1 = ρ2 = ρ3 = ρ4 = ρ = ρ5
= const.
- Nhiệt độ của bình chứa trao đổi với môi trường là không đáng kể.
b) Phương trình vi phân biểu diễn hệ thống.
* Áp dụng định luật bảo toàn năng lượng cho bình 1 ta có:
2514511
2
1
224511
21
h)FF(hFhF
dt
dh
V
hFhFhF
dt
)hV(d
Thay h = CT và coi nhiệt dung riêng C của tất cả chất lỏng trong bình là như nhau
ta được:
2514511
2
1T)FF(TFTF
dt
dT
V (22)
* Áp dụng định luật bảo toàn năng lượng cho bình 2 ta có:
453133251
4
2
4543322
42
h)FFF(hFh)FF(
dt
dh
V
h)FF(hFhF
dt
)hV(d
Thay h = CT
453133251
4
2T)FFF(TFT)FF(
dt
dT
V (23)
c) Phân tích bậc tự do của hệ thống.
Ta thấy hệ thống có 7 biến quá trình T1, T2, T3, T4, F1, F3, F5 và 2 phương trình vi
phân. Như vậy số bậc tự do của hệ thống là 7 – 2 = 5, đúng bằng số biến vào. Điều này
cho biết mô hình ta đã xây dựng được là chính xác.
Hệ thống có 5 bậc tự do nghĩa là ta có thể xây dựng được 5 vòng điều khiển độc lập
cho 5 biến vào. Tuy nhiên nhiệt độ là một biến quá trình gây nhiều khó khăn trong đo
lường và điều chỉnh vì thế ta lựa chọn hai biến vào lưu lượng F1 và F3 làm biến điều
khiển và xây dựng hai vòng điều khiển cho hai biến vào này.
d) Tuyến tính hoá phương trình.
Tại có phương trình làm việc tại điểm cân bằng
2514511
2
1T)FF(TFTF
dt
Td
V
45313321
4
2T)FFF(TFTF
dt
Td
V
Hai phương trình (22) và (23) đều là phi tuyến, do đó ta tuyến tính hoá nó tại điểm
làm việc.
Đặt y1 = ∆T2, y2 = ∆T4, u1 = ∆F1, u2 = ∆F3, d1 = ∆T1, d2 = ∆T3, d3 = ∆F4, d4 = ∆F5
* Tuyến tính hoá phương trình (22)
)T,T,T,F,F(fT)FF(TFTF
dt
dT
V4215112514511
2
1
2
4
1
1
2
1
1
1
1
4
5
1
1
1
1
421511
1
1y
dT
df
y
dT
df
d
dT
df
d
dF
df
u
dF
df
)T,T,T,F,F(f
dt
dy
V
)s(yG)s(dG)s(dG)s(uG)s(y
)s(y
FFsV
F
)s(d
FFsV
F
)s(d
FFsV
TT
)s(u
FFsV
TT
)s(y
)s(yF)s(dF)s(u)TT()s(u)TT()s(y)FFsV(
yFy)FF(dFd)TT(u)TT(0
dt
dy
V
241342111
2
511
5
1
511
1
4
511
24
1
511
21
1
25112241211511
2515111424121
1
1
* Tuyến tính hoá phương trình (23)
Đặt y1 = ∆T2, y2 = ∆T4, u1 = ∆F1, u2 = ∆F3, d1 = ∆T1, d2 = ∆T3, d3 = ∆F4, d4 = ∆F5
)T,T,T,F,F,F(fT)FFF(TFT)FF(
dt
dT
V4325312453133251
4
2
)s(d
FFFsV
TT
)s(u
FFFsV
TT
)s(u
FFFsV
TT
)s(y
)s(dF)s(y)FF()s(d)TT()s(u)TT()s(u)TT()s(y)FFFsV(
y)FFF(dFy)FF(d)TT(u)TT(u)TT(0
dt
dy
V
y
dT
df
d
dT
df
y
dT
df
d
dF
df
u
dF
df
u
dF
df
)T,T,T,F,F,F(f
dt
dy
V
4
5312
42
2
5312
43
1
5312
42
2
2315144224314225312
253123151442243142
2
2
2
4
2
2
3
2
1
2
2
4
5
2
2
3
2
1
1
2
4325311
2
2
)s(d
FFFsV
F
)s(y
FFFsV
FF
2
5312
3
1
5312
51
)s(d
FFFsV
TT
)s(u
FFFsV
TT
)s(u
FFFsV
TT
)s(y 4
5312
42
2
5312
43
1
5312
42
2
)s(d
FFFsV
F
)s(y
FFFsV
FF
2
5312
3
1
5312
31
)s(dG)s(yG)s(dG)s(uG)s(uG)s(y 29184726152
* Mô hình hàm truyền đạt của hệ thống
)s(yG)s(dG)s(dG)s(uG)s(y 241342111
)s(dG)s(yG)s(dG)s(uG)s(uG)s(y 29184726152
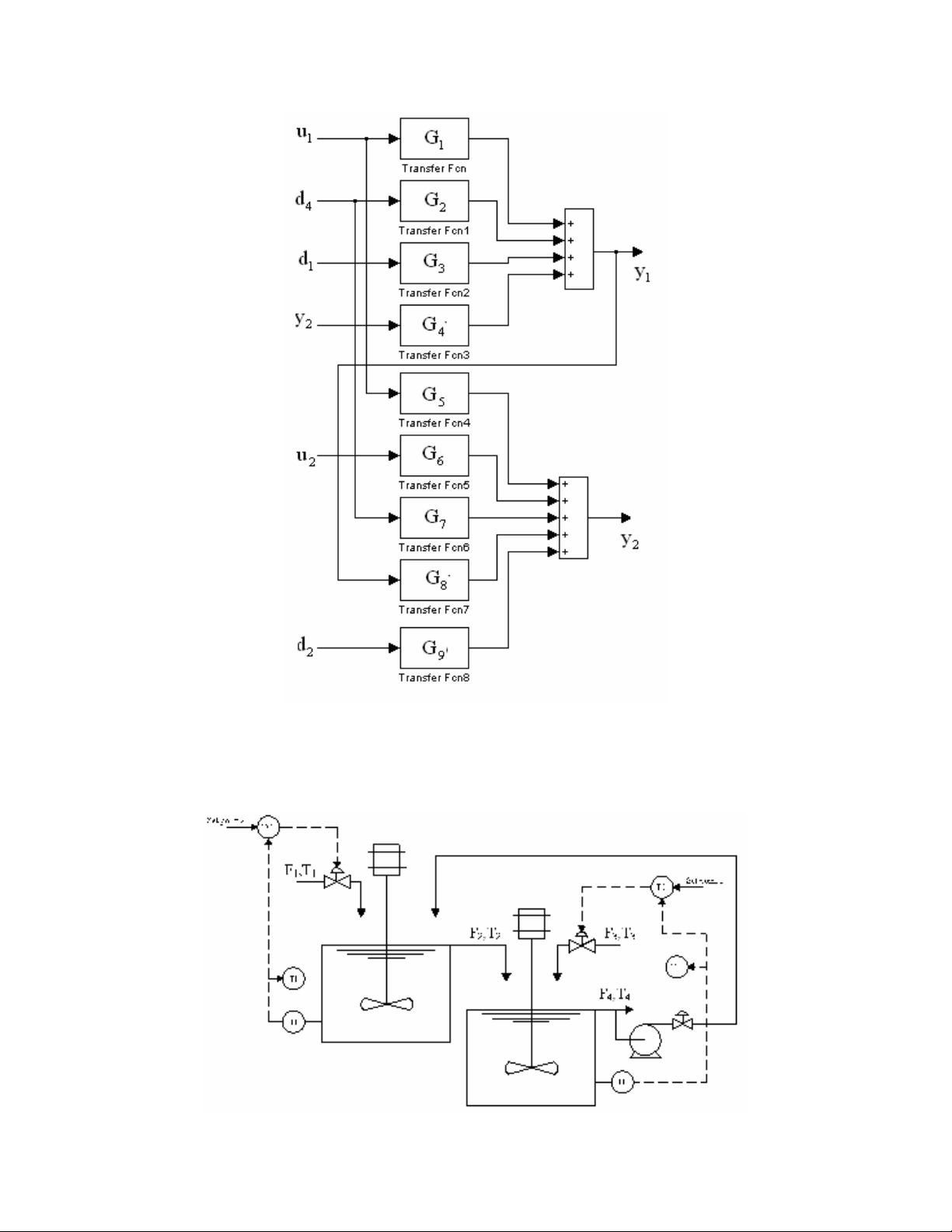
f) Lưu đồ P&ID
Ta lựa chọn bộ điều khiển mức ở đây là bộ điều khiển phản hồi PID với tín hiệu
vào ra là tín hiệu điện. Khi đó ta được lưu đồ P&ID như sau: