1
GI I TÍCH H TH NG ĐI N Ả Ệ Ố Ệ
GI I TÍCH H TH NG ĐI N Ả Ệ Ố Ệ
NÂNG CAO
NÂNG CAO
Võ Ng c Đi uọ ề
B Môn H Th ng Đi nộ ệ ố ệ
Khoa Đi n – Đi n tệ ệ ử
Tr ng ĐH Bách Khoaườ
CH NG 3: PHÂN B CÔNG SU TƯƠ Ố Ấ
2
V n Đ Phân B Công Su tấ ề ố ấ
Công c quan trong nh t và cũng ph bi n nh t trong phân ụ ấ ổ ế ấ
tích hê th ng đi n:ố ệ
- Đ c bi t nh là l i gi i “phân b t i” (load flow)ượ ế ư ờ ả ố ả
- Đ c s d ng đ quy ho ch và đi u khi n h th ng đi n.ượ ử ụ ể ạ ề ể ệ ố ệ
- Gi s : đi u ki n cân b ng và phân tích đ n pha.ả ử ề ệ ằ ơ
V n đ : ấ ề
- Xác đ nh biên đ và góc đi n áp m i nút.ị ộ ệ ở ỗ
- Xác đ nh phân b công su t th c và kháng trên m i đ ng dây.ị ố ấ ự ỗ ườ
- M i nút có 4 bi n tr ng thái:ỗ ế ạ
+ Biên đ đi n áp.ộ ệ
+ Góc đi n áp.ệ
+ Công su t th c b m vào.ấ ự ơ
+ Công su t kháng b m vào. ấ ơ
3
V n Đ Phân B Công Su tấ ề ố ấ
M i nút có 2 trong s 4 bi n tr ng thái là xác đ nh đ c ho c ỗ ố ế ạ ị ượ ặ
đã cho.
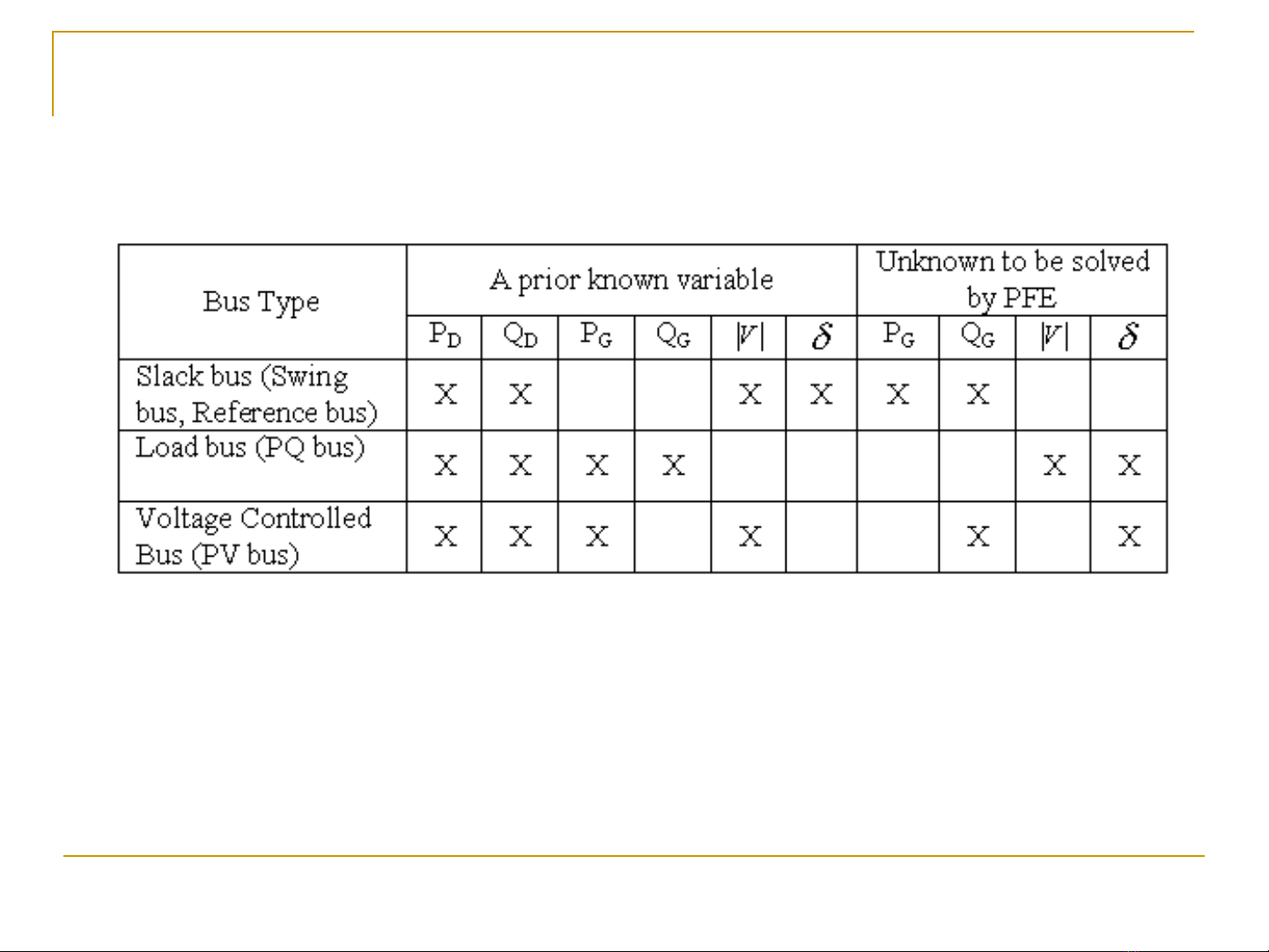
Các lo i nút trong h th ng:ạ ệ ố
- Nút t i (nút PQ):ả
Bi tế: Công su t th c P và công su t kháng Q c p cho t i.ấ ự ấ ấ ả
Ch a bi tư ế : Biên đ và góc đi n áp.ộ ệ
- Nút máy phát (nút PV):
Bi tế: Công su t th c P phát vào h th ng và biên đ đi n áp V.ấ ự ệ ố ộ ệ
Ch a bi tư ế : Công su t kháng và góc đi n áp.ấ ệ
- Nút chu n (slack bus, swing bus, reference bus)ẩ
Bi t:ế Biên đ và góc đi n áp.ộ ệ
Ch a bi tư ế : Công su t th c và công su t kháng.ấ ự ấ
* Ph i có 1 MF làm nút chu n và bù công su t vào h th ng do b i t n ả ẩ ấ ệ ố ở ổ
th t.ấ
4
V n Đ Phân B Công Su tấ ề ố ấ
Vi c phân lo i nút đ c th c hi n nh sau:ệ ạ ượ ự ệ ư
Chú ý: N u m t máy phát có đ ngu n công su t đ b o ế ộ ủ ồ ấ ể ả
đ m m t m c đi n áp nào đó, nó đ c x lý nh là m t nút ả ộ ứ ệ ượ ử ư ộ
đi u ti t đi n áp.ề ế ệ
5
Ph ng Trình Phân B Công Su tươ ố ấ
Đ nh lu t Kirchhoff v dòng đi n:ị ậ ề ệ
Đ nh lu t phân b công su t:ị ậ ố ấ