1
Expected Utilit
y
Theor
y
under Uncertainty
Lý thuyết Lựa chọn của Nhà Đầu tư
ề ắ ắ
trong đi
ề
u kiện không ch
ắ
c ch
ắ
n
1. Giới thiệu
• Chúng ta đã nghiên cứu về lý thuyết sự lựa chọn của
nhà đầu tư trong điều kiện chắc chắn
• Trong thực tế, quyết định của nhà đầu tư thường được
thựchiện trong điềukiện không chắcchắn
thực
hiện
trong
điều
kiện
không
chắc
chắn
•Ví dụ:
1. Không chắc chắn về chất lượng (xe cũ)
2. Không chắc chắn về hành vi của đối tác
-> Kết quả phụ thuộc vào hành vi của đối tác
2
3. Mua tài sản tài chính (cổ phiếu và trái phiếu) lợi
suất phụ thuộc vào biến động thị trường.
Đây là nội dung nền tảng của Kinh tế học Tài chính
2
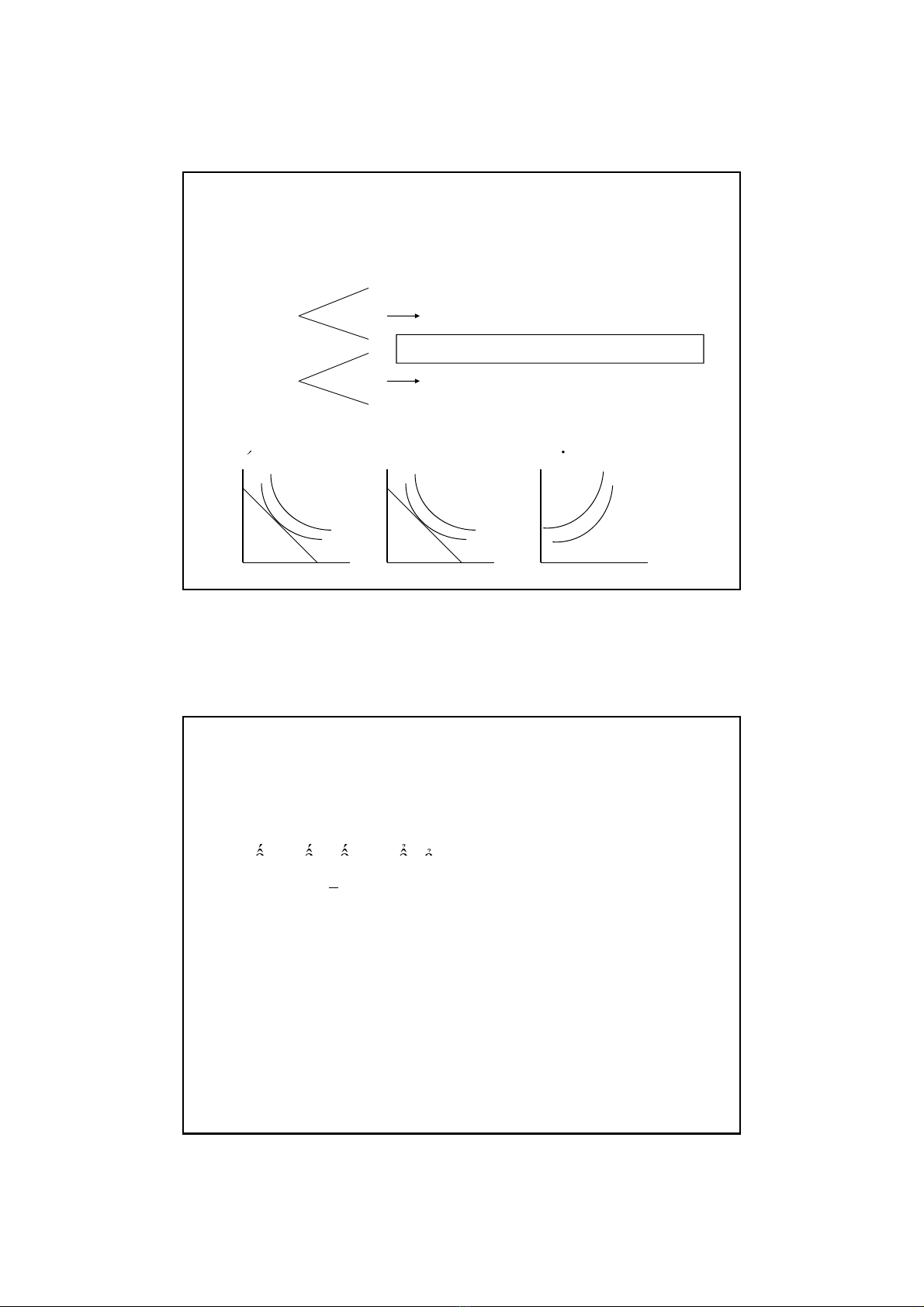
Mục tiêu của cá nhân
1) Các cá nhân tối đa hóa độ thỏa dụng kỳ vọng
0.4 10
Ati
E(W) = 0.4(10) + 0.6(2) = 5.2
0.3
0.6
0.7
2
2
)
Sở thích của cá nhân đối với l
ợ
i suất và rủi ro
9
4
A
sse
t
i
Asset j E(W) = 0.3(9) + 0.7(4) = 5.5
E[U(W)] = 0.4U(10) + 0.6U(2) = ?
E[U(W)] = 0.3U(9) + 0.7U(4) = ?
Nhà đầu tư thích E[U(W)] cao hơn
3
)ợ
y
x
C2
C1
Return
Risk
Xác suất
• Xác suất là khả năng một biến cố có thể xuất hiện
sau nhiều phép thử
•Nếu αi= là xác suất biến cố i xuất hiện trong tổng
số
n
biếncốcó thểxảyra
số
n
biến
cố
có
thể
xảy
ra
•1. αi>0, i = 1…n
•2. ∑αi= 1
•Giả sử (X) là giải thưởng
•X
1, X2, X3,...,Xncó xác suất tương ứng αi
•α
1
, α
2
, α
3
,...,α
n
, là xun
g
khắc và hoàn chỉnh
‘i=1
n
4
1
2
3
n
g
(mutually exclusive and exhaustive)
• Thì giá trị kỳ vọng của giải thưởng là
• E(X) = α1X1+ α2X2+ α3X3+ ... + αnXn
• E(X) = ∑αiXi
‘i=1
n

3
Ví dụ 1
•Đánh bạc (X) tung đồng xu
•
Nếu
n
gửa,
nh
ậ
n
$
1 X
1
= +1
Nếugửa, ậ$
1
•Nếu sấp, trả $1 X2= -1
• E(X) = (0.5) (1) + (0.5) (-1) = 0
•Nếu chúng ta chơi nhiều lần, khả năng chúng ta hòa vốn
rất lớn
5
Thí dụ 2
•Đánh bạc (X) tung đồng xu
•Nếu ngửa, thắng $10 X1= +10
•Nếu sấp, thua $1 X2= -1
• E(X) = (0.5) (10) + (0.5) (-1) = 4.50
•Nếu chúng ta chơi nhiều lần, chúng ta sẽ thắng lớn
• Chúng ta sẵn sàng trả bao nhiêu để chơi trò chơi này:
Có hểhiềhấlà $4 0
6
•
Có
t
hể
n
hiề
u n
hấ
t
là
$4
.5
0
•Câu trả lời phụ thuộc vào sở thích đối với rủi ro

4
Ván bài công bằng
•Nếu
the cost to play = expected value of
these gambles the outcome
– Ván bài công bằng về mặt thống kê - actuarially fair
•Thực tiễn chứng minh:
1. Thông thường mọi người đồng ý tung đồng xu trong trường hợp
số tiền nhỏ và từ chối chơi trong trường hợp số tiền lớn
7
2. Mọingườisẵnsàngbỏsốtiềnnhỏđểchơibạc không công bằng
vềmặtthống kê actuarially unfair games (Lotto 649, where cost = $1,
but E(X) < 1) nhưng sẽtừchốichơi nhiều
St. Petersburg Paradox
• Ván bài (X):
•Một đồng xu sẽ được tung n lần cho đến khi ngửa, bạn nhận được$2
n
hái
$2
$4
$8
$2
•Trạng t
hái
:X
1=
$2
X2=
$4
X3=
$8
... Xn=
$2
n
• Xác suất: α1= 1/2 α2= 1/4 α3= 1/8 ... αn= 1/2n
E(X) =
Paradox: Khôngaicóthểchơivánbàinàycôngbằng vềmặtthống kê
“
actuarially
fair
”
∞===
∑∑ ∑
∞
=1
12
2
1
i
i
i
ii x
α
8
actuarially
fair

5
St. Petersburg Paradox
nP(n)Prize
Expected
payoff
1 1/2 $2 $1
2 1/4 $4 $1
3 1/8 $8 $1
4 1/16 $16 $1
5 1/32 $32 $1
9
6 1/64 $64 $1
7 1/128 $128 $1
8 1/256 $256 $1
9 1/512 $512 $1
10 1/1024 $1024 $1
Giải thích St. Petersburg Paradox
•Giả sử U(X) = ln(X) U'(X)=1/x > 0 MU dương
• U"(X)=-1/x2< 0 MU giảm dần
• E(U(W)) = E(ΣαiU(Xi)) = (Σαiln(Xi)) = 1.39 < ∞
• Các cá nhân có thể trả 1.39 đơn vị độ thỏa dụng để chơi trò
chơi này
10


























