Ch

ng V

ươ

N i Dung

ộ

ng c m ng đi n t là gì? ệ ừ

ả ứ ậ ơ ả

1. Hi n t ệ ượ 2. Các đ nh lu t c b n. ị ng D ng c a hi n t 3. ng c m ng đi n ụ ủ ệ ượ ả ứ ệ

Ứ .ừ t

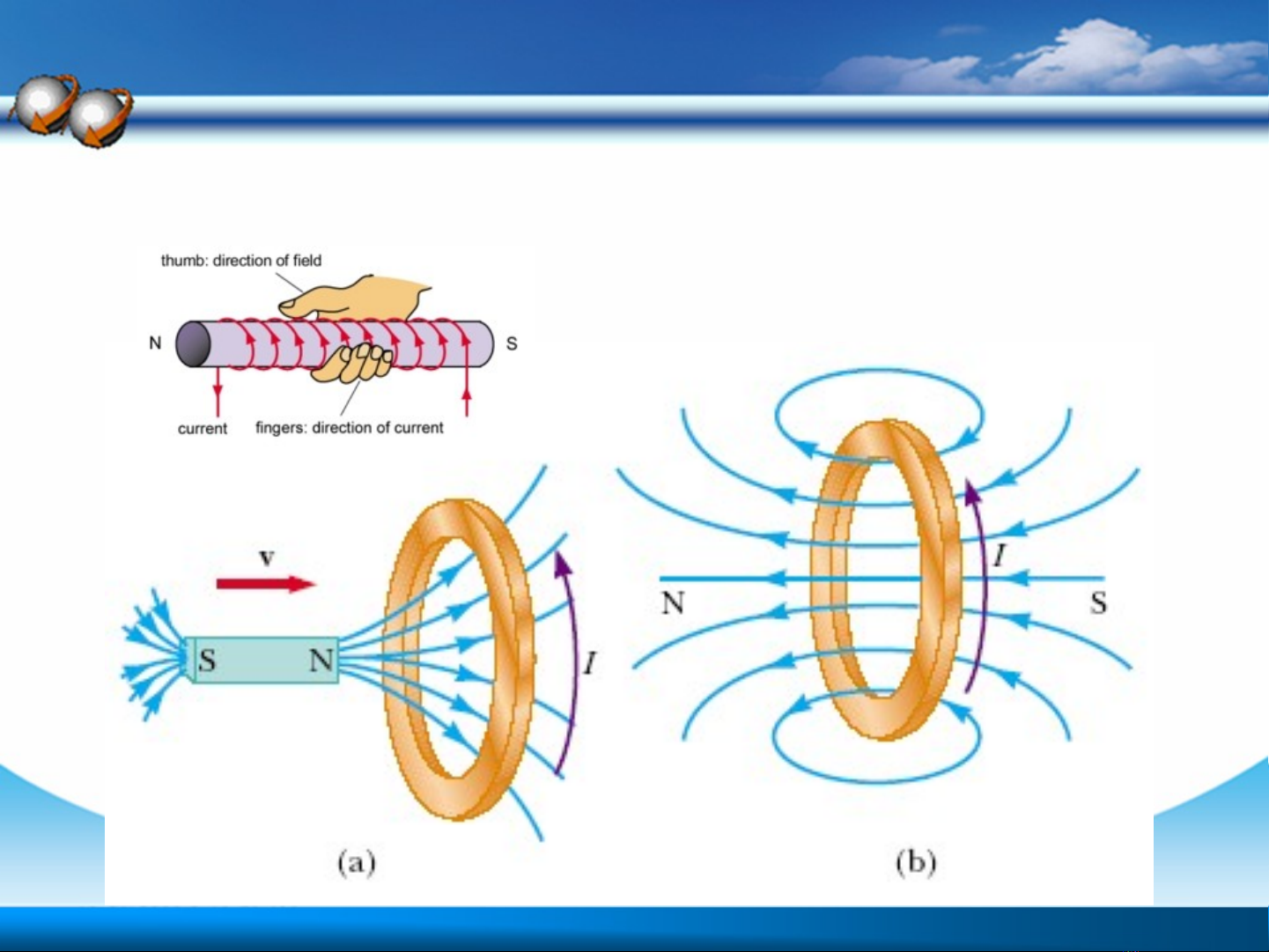
Hi n t

ng c m ng đi n t

ệ ượ

ả ứ

ệ ừ

1. Hai thí nghi m c a Faraday ệ ủ

Hi n t

ng c m ng đi n t

ệ ượ

ả ứ

ệ ừ

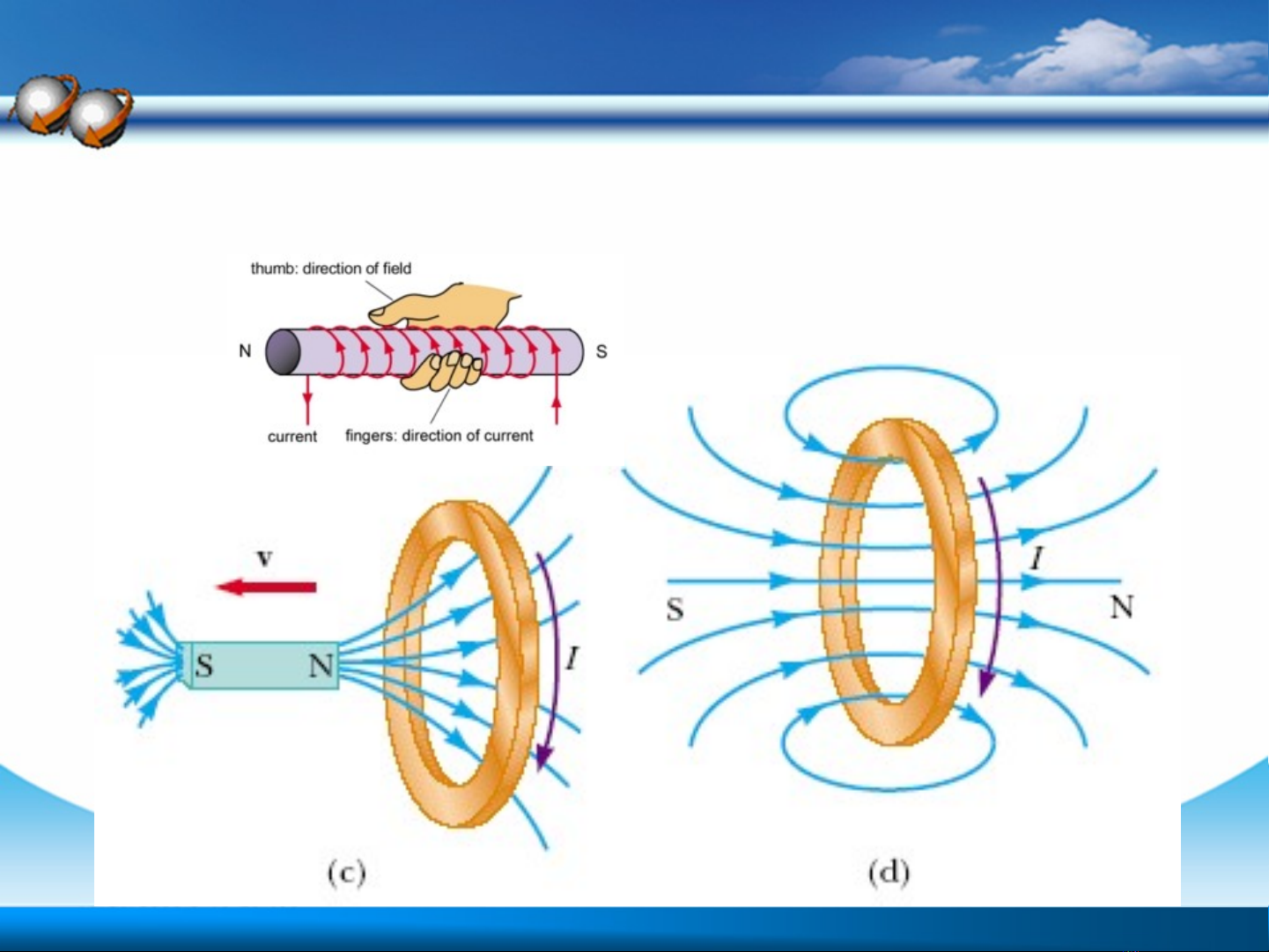
1. Hai thí nghi m c a Faraday ệ ủ

Hi n t

ng c m ng đi n t

ệ ượ

ả ứ

ệ ừ

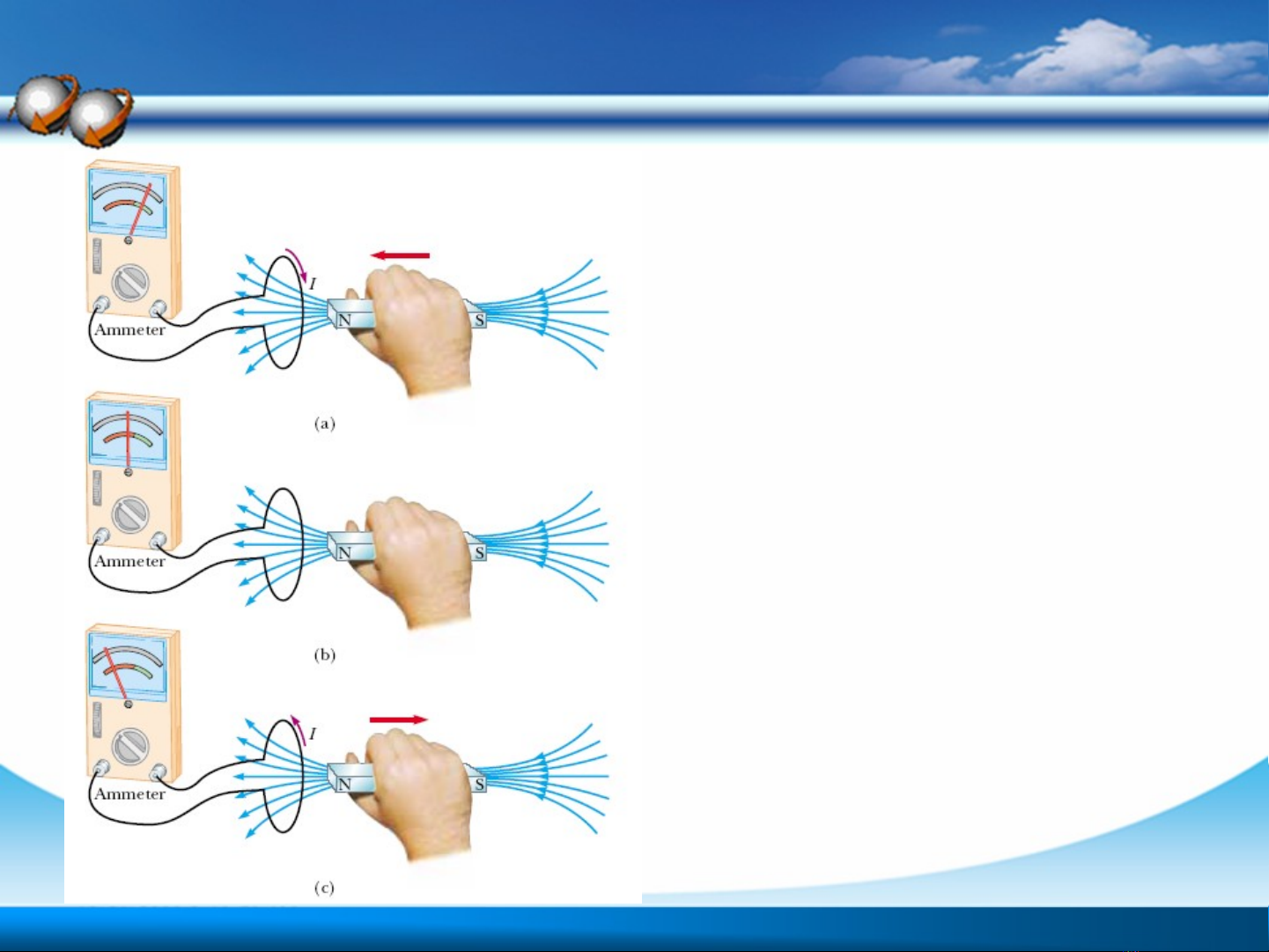
1. Khi đ a nam châm

l 2. Gi

ệ ư

ư i g n vòng dây. ạ ầ vòng dây và ữ nam châm đ ng ứ yên, không có dòng đi n qua Ampe k . ế 3. Đ a nam châm ra xa vòng dây.

Hi n t

ng c m ng đi n t

ệ ượ

ả ứ

ệ ừ

ấ

ớ ộ ệ ư ậ ổ

ậ

ổ

ệ

đây là

ự

ổ ể ấ

Nh v y ta th y, ch khi “có cái gì” đó ỉ thay đ i thì m i có su t đi n đ ng c m ng. ả ứ ấ tr ng thái tĩnh, không có v t nào di Ở ạ chuy n, và dòng đi n là không đ i thì không ệ ể có s c đi n đ ng c m ng ả ứ ộ ứ V y ta th y r ng đi u then ch t ậ ố ở ề ấ ằ ổ ”. Th nh ng câu h i đ t ra là “s thay đ i ỏ ặ ế ư “cái gì đó” ph i thay đ i đ sinh m t su t ộ ả đi n đ ng c m ng là cái gì? ả ứ ệ ộ

Đ nh lu t c m ng c a Faraday

ậ ả ứ

ủ

ị

ả ứ ệ ấ

Vòng dây ch có su t đi n đ ng c m ng ộ đi qua vòng dây đó thay ng s c t ỉ ứ ừ ố ườ

khi s đ đ i.ổ

ổ ể

ả ứ

ộ ng s c t s ố ứ ừ đi qua vòng dây đó. Và “s thay

” c a s đ ự ủ ố ườ ự ế

ng ố ộ ế

quy t đ nh đ l n c a ứ ừ ế ị

V y “ậ cái gì đó” thay đ i đ sinh m t s c ộ ứ đi n đ ng c m ng trong vòng dây chính là ệ đ ườ đ iổ ” chính là “s bi n thiên đi qua vòng dây. Và chính t c đ bi n s c t ứ ừ thiên c a đ ộ ớ ủ ủ ườ s c đi n đ ng c m ng. ộ ệ ứ ng s c t ả ứ

Đ nh lu t c m ng c a Faraday

ậ ả ứ

ủ

ị

ượ

ở

f thông ể i h n b i m t vòng dây ộ ớ ạ ng s c t đi qua di n tích này ệ ứ ừ B đi qua di n ệ ừ ằ

Kh o sát đ nh l ng ị ả Xét m t di n tích gi ệ ộ d n kín. S đ ố ườ ẫ c bi u di n b ng t đ ễ ượ tích đó

Đ nh lu t phát bi u nh sau

ị

ể

(cid:0) uur r B dA (cid:0) f = B

ậ ấ ẫ

ộ

ư Su t đi n đ ng c m ng trong m t vòng ộ ả ứ dây d n b ng nh ng trái d u v i t c đ bi n ớ ố ộ ế ấ thiên theo th i gian c a t thông qua vòng dây ủ ừ ờ đó.

ệ ằ ư

Đ nh lu t c m ng c a Faraday

ậ ả ứ

ủ

ị

Nghĩa là ta có th vi ể ế

f

x = -

thông tính b ng ế ố ộ ế

ả ứ ệ

t nh sau ư Bd dt N u t c đ bi n thiên t ằ ừ Vebe/s thì s c đi n đ ng c m ng là V. ộ ứ N u cu n dây có N vòng dây ế ộ

Đ nh lu t c m ng c a Faraday

ậ ả ứ

ủ

ị

ậ

T thông

ừ

ệ

ng h p ng dây có nhi u ề

Cái gì đó thay đ i ổ theo th i gian ờ

Đ nh lu t Faraday cho ị tr ợ ố ườ 2. Đ nh lu t Faraday ị ậ vòng Su t đi n ấ c mả

Hi n t

ng c m ng đi n t

ệ ượ

ả ứ

ệ ừ

1. S bi n đ i c a t thông qua m ch kín là ổ ủ ừ ự ế

ạ ệ ả ứ

i trong m ch 2. Dòng đi n c m ng ch t n t ệ ả ứ nguyên nhân sinh ra dòng đi n c m ng. ạ

ừ

thu n ậ ộ

thông g i qua m ch thay đ i. ổ ử 3. C ng đ dòng đi n c m ng t l ỉ ệ thông. khi t ườ v i t c đ bi n đ i c a t ớ ố ộ ế

ụ

vào t ỉ ồ ạ ạ ệ ả ứ ổ ủ ừ 4. Chi u c a dòng đi n c m ng ph thu c ệ ả ứ thông g i qua m ch tăng hay gi m. ạ ề ủ ừ ộ ả ử

K t lu n

ế

ậ

ng xu t hi n dòng đi n ậ ệ

ọ

ạ

V y, hi n t ấ ệ ượ trong m ch kín khi t ừ ạ bi n thiên g i là hi n t ế đi n t ệ ừ dòng đi n c m ng. ệ thông qua m ch ạ ng c m ng ả ứ ệ ượ . Dòng đi n trong m ch g i là ọ ệ ệ ả ứ

Đ nh lu t Lenzt ậ

ị

1. Đ nh lu t Lenzt ậ ị

ệ ị

ậ ả ứ

ắ ể ị

ề ủ ọ ậ ị

Ba năm sau khi Faraday phát hi n đ nh lu t c m ng. Heinrich Friendrich Lenz đ a ư ra qui t c đ xác đ nh chi u c a dòng đi n ệ c m ng trong vòng dây g i là đ nh lu t ả ứ Lenz.

ệ ấ

ệ ả ứ ẫ

Dòng đi n c m ng xu t hi n trong m t ộ vòng dây d n kín có chi u sao cho nó ch ng ố ề i s thay đ i c a tác nhân đã sinh ra nó. l ạ ự ổ ủ

Đ nh lu t Lenzt ậ

ị

Chi u c a ngón tay cái là ề ủ ng c m tr chi u c a t ả ề ủ ừ ườ ng.ứ

Đ nh lu t Lenzt ậ

ị

ả i thích cho thí nghi m th nh t ứ ấ ệ

Hai cách gi Cách gi i thích th nh t: ả ứ ấ

ệ

ng nên nó cũng có c c b c và nam. N u ườ ộ ừ ế

ố

ạ ự ướ ế

ố

ự ắ ắ

ề

ệ ồ

Vì dòng đi n trong vòng dây sinh ra m t t tr ự ắ i s chuy n đ ng c a thanh vòng dây ch ng l ủ ộ ể i g n nó c h t là c c b c l nam châm mà tr ự ắ ạ ầ thì m t c a vòng dây đ i di n thanh nam ệ ặ ủ châm ph i là c c b c. Áp d ng qui t c bàn ụ ả tay ph i cho vòng dây. Khi đó chi u dòng ả c chi u kim đ ng h khi ta đi n ph i ng ồ ề ượ ả phía thanh nam châm. nhìn vòng dây t ừ

Đ nh lu t Lenzt ậ

ị

Đ nh lu t Lenzt ậ

ị

Cách gi i thích th hai ả ứ

ầ ư

ừ

ố t l p t i s ạ ự ng ệ ả ứ ổ

ng

ượ

ả ằ ị

ệ ả ứ ượ

ề ủ

Vì khi ta đ a thanh nam châm đ n g n vòng ế thông qua vòng dây. Dòng dây là làm tăng t đi n c m ng trong vòng dây ch ng l ế ậ ừ ườ Bi tr thay đ i này b ng cách thi ằ i s tăng c a thông c a chính nó, đ ch ng l ể ố ạ ự ủ ủ Tr ư ậ ừ ườ Bi ph i h ng. Nh v y t ng l ả ướ ượ thông sinh b i nam châm. c chi u v i t ng ở ớ ừ ề Cũng b ng qui t c bàn tay ph i ta xác đ nh ắ đ c chi u c a dòng đi n c m ng trong vòng dây.

Đ nh lu t Lenzt ậ

ị

ạ ả ứ

ng c a thanh nam châm.

i ng c m ng không ch ng l ố Nó ch ch ng ỉ ố . Và n u ta ế

thông qua vòng

thông qua nó ừ ả ứ ứ

ừ ườ i s gi m c a t ủ ừ

ng c m ng ng lúc này thông b ng cách ằ ng m nh lên. Chi u c a dòng ề ủ ạ ề ụ ấ ẽ ớ

phía thanh ừ

L u ýư : T tr ừ ườ tr t ủ ừ ườ l i s thay đ i c a t ổ ủ ừ ạ ự kéo thanh nam chân ra xa, t dây s gi m. T tr ẽ ả s ch ng l ạ ự ả ẽ ố tr làm cho t ừ ườ đi n t o ra tác d ng y s cùng chi u v i kim ệ ạ đ ng h n u ta nhìn vòng dây t ồ ế ồ nam châm.

Đ nh lu t Lenz và s b o toàn năng l ng ự ả ậ ị ượ

thi ế ệ

ế ộ

Th đ t gi t xem n u nh dòng đi n ư ả ử ặ c m ng ng h tác nhân đã sinh ra nó thì ả ứ ủ đi u gì s x y ra? ề ẽ ả

ư ậ

ẩ ự ắ ủ

i xu t hi n ủ ặ ng h p khi ta ợ i g n vòng ạ ầ ệ ạ ấ

Nh v y nghĩa là trong tr ườ đ y c c b c c a nam châm l dây, thì m t này c a vòng dây l c c nam. ự

Đ nh lu t Lenz và s b o toàn năng l

ng

ự ả

ậ

ị

ượ

ế ư ậ

ấ ầ ẩ

ể

ứ ắ ầ duy trì

ể  nam châm s đ ẽ ượ ậ ộ c gia t c v ố ề ộ

ỏ

Và n u là nh v y thì lúc đ u nam châm ẹ  đang đ ng yên, ta ch c n đ y nó r t nh ỉ ầ nó b t đ u chuy n đ ng và chuy n đ ng này ộ t ự phía vòng dây và nó s nh n thêm đ ng năng ẽ trong quá trình này. Trong khi đó trong vòng dây cũng t a ra nhi t l ng. (do vòng dây có ệ ượ đi n tr ệ ứ ở  hi u ng Jun-lenx) ệ

Đ nh lu t Lenz và s b o toàn năng l

ng

ự ả

ậ

ị

ượ

h vô ta có th thu ư ậ ừ ư ể

Nh v y rõ ràng là t đ c m t cái gì đó !?! ượ ộ

ị ậ

ượ ợ ớ

Đ nh lu t Lenz không gì khác là s phát bi u ể ự nguyên lý b o toàn ả năng l ng d i d ng ướ ạ thích h p cho vi c áp ệ d ng v i các m ch ạ ụ đi n có dòng đi n ệ ệ c m ng ch y qua. ả ứ ạ

Đ nh lu t Lenz và s b o toàn năng l

ng

ự ả

ậ

ị

ượ

ẩ

ố ắ

ư ậ

ấ

ấ ằ ề

ố

ư ế

ộ

ằ

ệ

ỉ

ộ ự ệ ượ ệ ượ

ẫ

ng chuy n hóa l n nhau trong h cô ng

Nh v y ta th y r ng: cho dù ta c g ng đ y nam châm theo chi u nào ta cũng luôn v p ph i m t l c ch ng đ i, và nh th ta ph i ả ả ố th c hi n m t công. Theo nguyên lý b o toàn ả ự t năng ng, công này đúng b ng nhi năng l xu t hi n trong vòng dây vì ch có hai d ng ạ ấ năng l ệ ể l p này (th c ch t ượ ấ ở ậ ự m t đi d i d ng b c x là không đáng k ). ể ấ ướ ạ Th t ra, theo đ nh lu t Faraday ị ậ

f

đây ta đã coi năng l ứ ạ ậ Bd dt

x = -

Đ nh lu t Lenz và s b o toàn năng l

ng

ự ả

ậ

ị

ượ

ng tích tr trong t ữ ừ

Có nghĩa là năng l tr ngườ f

ượ Bd dt

x ể ượ

ng đi n tr ng Đã chuy n thành năng l ườ ệ trong vòng dây và do vòng dây có đi n tr ở ệ  nhi t năng do hi u ng Jun-Lenx ệ ứ ệ

Đi n tr ệ

ườ

ng c m ng ả ứ

ặ

ả ử tr ộ ừ ườ

ổ  dòng đi n và s c ệ

ệ

ả ứ ậ ộ ừ ị ề

ề

Đ t m t vòng dây đ ng bán kính r vào ộ ồ tr ng đ u. Tr ng này trong m t t ộ ừ ườ ườ ề choán đ y m t th tích hình tr bán kính R. ộ ầ ụ ể ng đ t Gi ng v i t c đ s tăng c ườ ớ ố ộ không đ i ổ  t thông qua vòng dây tăng ừ v i t c đ không đ i ứ ớ ố ộ đi n đ ng c m ng xu t hi n trên vòng ấ ệ  chi u dòng đi n dây. T đ nh lu t Lenz ệ c kim đ ng h . c m ng theo chi u ng ồ ồ ượ ả ứ Nh mô t trên hình v ẽ ư ả

Đi n tr ệ

ườ

ng c m ng ả ứ

Đ nh lu t Faraday ậ ị

c t o ra trong m t

ệ

ộ

ộ

ườ ẫ

ả ủ

ổ

ệ

ế

ng đ M t đi n tr ượ ạ vòng dây d n là k t qu c a vi c bi n đ i ế t ừ Công d ch chuy n ể q đi h t m t vòng

thông ị ộ ế

S t n t

i c a đi n tr

ng không ph thu c vào vi c

ự ồ ạ ủ

ệ

ườ

có hay không s hi n di n c a b t kỳ m t đi n tích th nào.

ụ ộ

ộ ệ

ệ ử

ệ ủ ấ

Nh v y, m t đi n tr

i cho dù không có m t vòng dây d n

ư ậ

ộ

ệ

ặ

ẫ

ự ệ ng v n t n t ườ

ẫ ồ ạ

Đi n tr ệ

ườ

ng c m ng ả ứ

ệ

ổ

ườ

ệ

ườ

ủ

ứ

ệ

Vì trên dây đ ng có dòng đi n ồ  t i m i đi m trên vòng dây ể ỗ ạ có đi n tr ng do s thay đ i ự ệ thông sinh ra. Đi n c a t ủ ừ ng c m ng này cũng có tr ườ ả ứ th c nh là đi n tr ng c a ệ ư ự các đi n tích đi m gây ra (ch ể ỉ ệ ng s c đi n khác là các đ ườ ng c m ng khép kín). tr

ả ứ

ườ

ng

ậ

ệ

ế

B t lu n ngu n g c th nào các đi n tr ườ đ u có tác d ng l c lên các đi n tích th . ử

ồ ụ

ấ ề

ố ự

ệ

Đi n tr ệ

ườ

ng c m ng ả ứ

M t t

ng thay đ i sinh ra m t đi n tr

ng.

tr ộ ừ ườ

ệ

ộ

ổ

ườ

T đó ta có th kh ng đ nh m t đi u r ng: ề ằ ừ ể ẳ ộ ị

ả

ụ

ộ

ườ ng s c đi n tr ng do t ả ứ ệ

ườ đây là m t h các đ ộ ọ ng c sinh ra. tr ng ừ ườ ng tròn ườ

Ngay c khi không có vòng dây đ ng thì ồ tr trong vùng không gian tác d ng c a t ủ ừ ườ ng c m ng cũng đ m t đi n tr ượ ệ Và các đ ứ ườ thay đ i sinh ra ở ổ đ ng tâm. ồ

Đi n tr ệ

ườ

ng c m ng ả ứ

ng đi n t ệ

ộ

c m ng trong m t Tr ộ ệ ừ ả ứ m ch đi n, m t cách tr c ti p t l ự ế ỉ ệ thông qua

ườ ạ v i t c đ bi n đ i t ớ ố ộ ế ổ ừ

m ch.ạ

Từ thông

Đi n tr ệ

ườ

ng c m ng ả ứ

ng c m ng b i s ở ự ng trong

ả ứ tr

Đi n tr ệ ườ thay đ i c a t ổ ủ ừ ườ cu n dây ộ

ắ ạ

ệ

Nguyên t c t o dòng đi n xoay chi uề

AC Generator

= NBScos(w

t + j )

m = NBScosa

http://sdsu-physics.org/physics180/physics196/Topics/faradaysLaw.html#maxwell

F

Nguyên t c t o dòng đi n m t chi u

ắ ạ

ộ

ề

ệ

Direc Generator

Su t đi n đ ng c m ng

ệ ộ

ả ứ

ấ

ấ ệ ộ ộ

ng Su t đi n đ ng trong m t thanh d n đi n ệ ẫ tr d ch chuy n ngang qua t ừ ườ ể ị

đ uề

ệ ầ ủ ụ

Các đi n tích b đ y v ị ẩ ề hai đ u c a thanh d i ướ tác d ng c a l c t ủ ự ừ hình thành nên m t ộ đi n tr ng trong ườ ệ thanh

ấ

ệ

ế ữ

ầ

Xu t hi n s chênh ệ ự l ch đi n th gi a hai ệ đ u thanh ngay khi thanh d ch chuy n liên

ị

ng

ể tr ừ ườ

t c qua t ụ

đ uề

Su t đi n đ ng c m ng ấ ệ ộ ả ứ

T thông

ừ

Đ nh lu t Faraday ậ

ị

i

ị

ạ

ậ ả

D ch chuy n ch ng l ố ể chuy n đ ng c a ủ ộ ể thanh

Đ nh lu t b o toàn đòi ị h iỏ

Dòng đi n Foucault

ệ

B

fi

Dòng đi n Foucault ệ

ạ

ấ

ấ ằ

ứ ấ

tr ừ ườ

ừ

ạ

ệ

ề ặ ấ ấ

ượ

ấ

Ta th y r ng khi t m kim lo i v trí th nh t, nó dang di ở ị ng chuy n ngang qua t ể khi đó t thông xuyên qua di n ệ tích b m t t m kim lo i đang tăng xu t hi n dòng đi n ệ c m ng theo đ nh lu t Lenz ả ứ ậ ị c chi u kim có chi u ng ề ề đ ng h nh hình v . Khi nó di ồ ư ẽ ồ thông qua chuy n v v trí 2 t ừ ể ề ị nó đang gi m ả  xu t hi n ệ ấ dòng đi n theo chi u kim đ ng ồ ệ ề tác d ng lên t m h . L c t ụ ồ ự ừ i hai v trí có chi u kim lo i t ề ị ạ ạ nh hình v . ẽ

ư

Dòng đi n Foucault ệ

ng d ng c a dòng Foucault

Ứ

ụ

ủ

Làm phanh điện  cho tàu hoả

ộ ấ ẽ

s d ng c treo

ấ ườ

ấ ớ ự ị

ả ứ ệ

ườ

ườ

ng này ch ng ng bên trong nam châm ng sinh b i các dòng Faucault ở

i. ệ ậ ế ạ Hình v cho th y m t phanh đi n t ệ ừ ử ụ dòng Faucault. M t nam châm đi n đ ộ ệ ượ trên toa xe l a g n v i đ ng ray. Đ d ng ể ừ ớ ườ ử ầ toa xe, ng i ta c p cho cu n dây c a nam ủ ộ châm đi n m t dòng r t l n. S d ch chuy n ể ệ ộ c a nam châm đi n làm c m ng các dòng ủ Faucault trên thanh ray. Các tr ố i s thay đ i c a tr l ổ ủ ạ ự tr đi n. Các t ừ ườ ệ tác d ng l c lên dòng đi n trong nam châm vì ự ụ th nó làm cho toa tàu ch m l

Máy bán hàng t

đ ng

ự ộ

Máy bán hàng tự động

ộ

ả

m t máy bán trên hình

ượ

ệ ơ đ ng có s d ng dòng Faucault đ ự ộ

ồ

ệ

ở ủ

ộ

ế

ệ

ư

ừ ộ c mô t ả ẽ ị ậ ạ c ki m tra b ng ể ẽ ượ ệ ế

ố

ồ i và đi qua m t t ướ

i ngay ằ ở ủ c ti p t c di chuy n ể ượ ế ụ tr ộ ừ ườ

ẽ ấ

ồ

ự

ẽ

ể

ậ

ng trên đ ng kênh s xu t hi n các dòng Faucault và l c ệ i. S chuy n ạ ộ ợ ậ

ủ

ầ

ạ ủ ẽ

ể

ị

ồ

ậ

ở

ồ

ẽ ượ

M t vi c đ n gi n nh là mua m t cái bánh t ư ộ hàng t ử ụ v . Sau khi ta cho ti n vào máy, đ ng kênh s b ch n l ề ẽ l p t c. Trong lúc đó đi n tr c a nó s đ ậ ứ cách đ a m t hi u đi n th ngang qua nó. N u đi n tr c a nó ệ l t vào vùng cho phép. Đ ng kênh đ ọ ng. Khi đi qua xu ng đo n d c bên d ạ ố t tr ự ừ ườ tác đ ng lên nó s làm nó chuy n đ ng ch m l t ể ộ ừ i c a nó ph thu c vào thành ph n h p kim c a đ ng ch m l ộ ụ ộ nó. Các sensor s đo t c đ c a nó sau khi nó di chuy n ngang ố ộ ủ c so sánh v i giá tr cho qua các nam châm. T c đ này s đ ớ ố ộ ẽ ượ phép. N u đ ng kênh đ t yêu c u nó s l t qua kh i vòng ki m ể ỏ ẽ ọ ạ ế ầ tra. C ng vào s đ c ch p nh n. c m ra và đ ng kênh đ ấ i, m t c ng khác s m ra và nó s b tr ra. Ng ẽ ở ộ ổ

ượ ẽ ị ả

ổ c l ượ ạ

Hi n t

ng t

c m

ệ ượ

ự ả

Hi n t

ng t

c m

ệ ượ

ự ả

Nh n xét ậ

ế ệ

ở

ừ ạ ệ

ng ạ ng này g i là hi n t ọ ấ ệ ượ ệ ượ

Khi dòng đi n qua m ch bi n thiên thì t ạ thông do chính dòng đi n này g i qua m ch ệ cũng bi n thiên làm trong m ch su t hi n sđđ ế c m ng. Hi n t ả ứ c m. t ự ả

Su t đi n đ ng t ệ ấ F

-=

L

tc

d m dt

)LI(d dt

dI dt

ộ -= c m: ự ả -= x

Hi n t

ng h c m

ệ ượ

ỗ ả

i đ t. Ng ị ộ ể

ể ướ ấ ạ ườ ặ ấ ế

i ta di chuy n m t máy dò kim t b này i ướ ế ị c kim lo i b vùi sâu d ạ ị ệ ượ

Đ dò tìm kho báu ho c dò mìn b chôn sâu ặ d lo i trên m t đ t. Làm th nào mà thi có th phát hi n đ l p đ t đá dày nhi u centimet ? ớ ể ấ ề

Hi n t

ng h c m

ệ ượ

ỗ ả

Su t đi n đ ng h c m ộ ỗ ả ệ ấ

m

f

hc

x = -

d dt

m

f ộ ừ

ở

m12

f thông do dòng đi n I ừ

m 21

f

i ta g i thông c a cu n là t ủ dây kia g i qua diên tích c a vòng dây đang xét ủ ệ 1 sinh ra và c l ọ ượ ạ

G i là t ọ g i qua di n tích vòng dây 2. Ng ệ ớ là D th y r ng ễ ấ ằ

m12

12

1

m 21

21

2

= = f f M I M I

Hi n t ng h c m ệ ượ ỗ ả

Ng i ta ch ng minh đ c r ng đ h c m ườ ứ ượ ằ ộ ỗ ả

ỗ ả ệ

M21 = M12 = M [H] Do đó su t đi n đ ng h c m xu t hi n trong ấ ộ ệ ấ vòng dây th hai là ứ

m12

1

hc 2

F d x = - = - M

dt dI dt

ấ ệ ấ

m 21

2

F

hc1

Và su t đi n đ ng h c m xu t hi n trong ỗ ả ộ ệ vòng dây th nh t là ứ ấ d = - x = - M

dt dI dt

V. ng d ng c a hi n t

ệ ượ

Ứ

ụ

ủ

ng c đt ư

Thi : 1. Đàn ghi ta đi nệ ế ị ế t b khu ch đ i có c u trúc ạ ấ

Ứ

ng d ng c a hi n t ủ

ệ ượ

ụ

ng c đt ư

ộ

t b bao ế ị ộ

ủ ự

ộ

thông (các đ ứ ừ ạ ườ ở

ổ  sinh ra dòng đi n ệ ộ

ộ ầ ổ ộ ề ộ

c n i v i m t thi Amplifier đ ượ ố ớ g m m t cu n dây qu n quanh m t lõi nam ấ ộ ồ ộ ng c a nam châm gây s phân châm. T tr ừ ườ c c S-N trên đo n dây đàn n m sát ngay trên ằ ạ ự nam châm  khi dây đàn dao đ ng làm cho t o b i dây đàn) ng s c t t ừ qua cu n dây thay đ i c m ng trong cu n dây. Vì dây đàn dao ả ứ  dòng đi n ệ đ ng lúc xa lúc g n cu n dây ộ trong cu n dây đ i chi u cùng v i t n s ớ ầ ố dao đ ng c a dây đàn. ủ ộ

Ứ

ng d ng c a hi n t ủ

ệ ượ

ụ

ng c đt ư

2. B p tế ừ

ộ

ộ ệ ư

ế ở ặ ạ

ượ ộ ướ ườ ệ

ở ớ  năng l ệ 

ượ ệ

Dòng đi n dao đ ng c đ a vào m t đ cu n dây n m ngay ằ i m t b p. T d ừ ng t o b i dòng tr đi n qua cu n dây s ẽ ộ dao đ ng ộ  sinh dòng ng dao đi n c m ệ ả ứ đ ng trong ch o. ộ ả ng đi n Vì ch o có đi n tr l n ệ ả ệ th t ra chính đi n tr c a t. ( ng nhi năng l ở ủ ậ ượ ) làm cho nó nóng lên th c ăn trong ch o t ả ự ứ