Nội dung
▪Quá trình quá độ trong mạch điện
➢Khái niệm
➢Các phương pháp giải mạch điện tuyến tính quá độ
▪Mạch điện phi tuyến
➢Mạch phi tuyến ở chế độ xác lập
(một chiều, xoay chiều)
➢Mạch phi tuyến ở chế độ quá độ
▪Đường dây dài
➢ĐDD ở chế độ xác lập, vấn đề truyền sóng
➢ĐDD ở chế độ quá độ, mô hình Peterson
3
➢Khái niệm chung về quá trình quá độ
➢Mô hình toán của quá trình quá độ
➢Hàm bước nhảy đơn vị và ứng dụng
➢Sơ kiện và phương pháp tính sơ kiện
▪Nguyên tắc tính sơ kiện
▪Hai luật đóng mở
▪Tìm sơ kiện cho bài toán quá độ
Chương 1
Quá trình quá độ trong mạch điện tuyến tính
4
▪QTQĐ xảy ra khi mạch bị kích động (đóng, cắt) làm cho
các thông số thay đổi đột ngột, dẫn đến thay đổi cấu trúc
của mạch điện.
•Trong mạch chứa các phần tử có quán tính- là các
phần tử tích trữ năng lượng (L, C): dòng điện trong
cuộn dây và điện áp trên tụ điện
W𝑚=
𝐿𝑖2
2
W𝑒=
𝐶𝑢𝐶
2
2
•Ví dụ mạch ở QTQĐ:
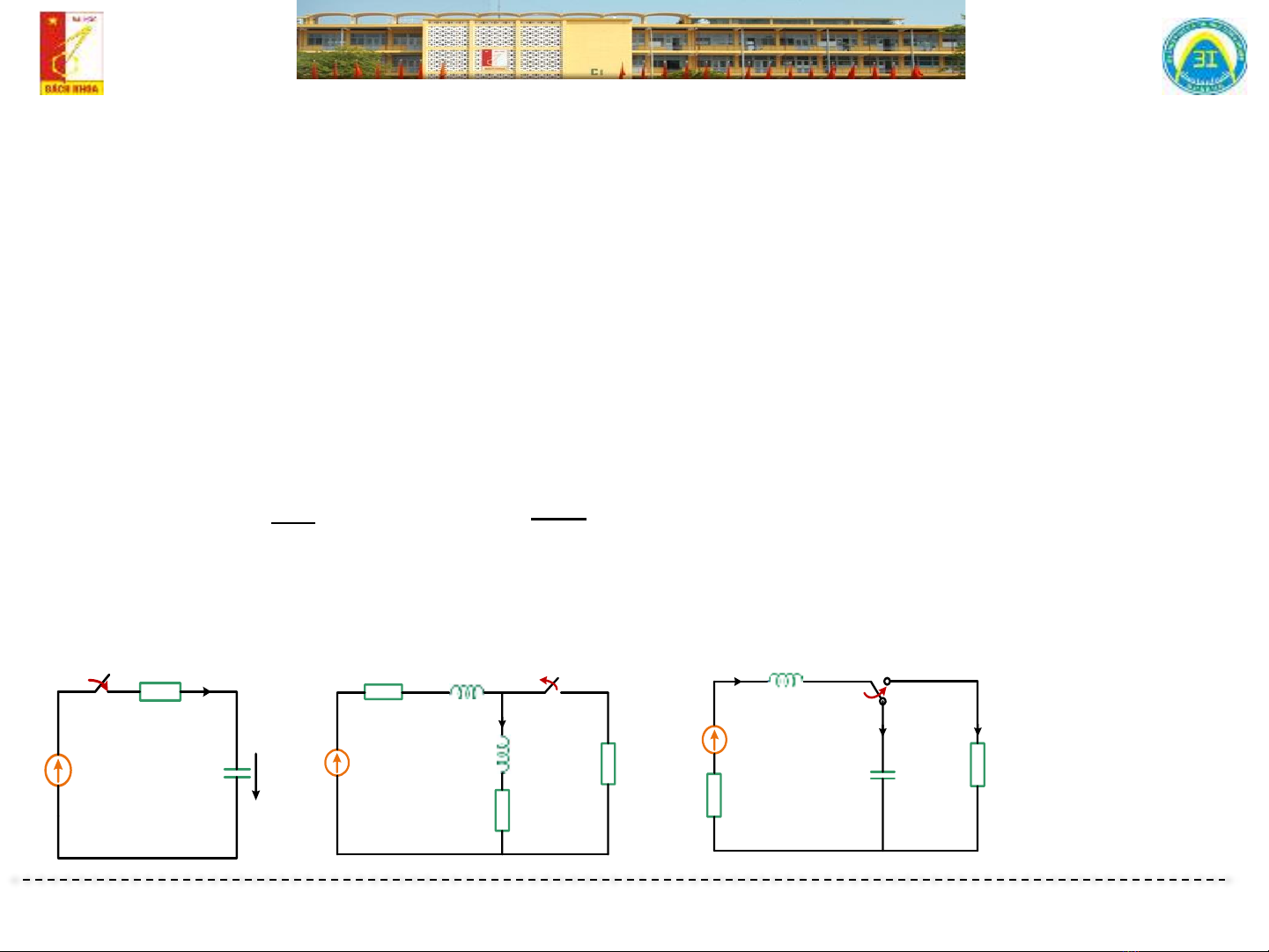
Khái niệm quá trình quá độ
Đóng khóa K Mở khóa K Chuyển khóa K từ vị trí 2 sang 1
E
K
R
C
()
C
ut
()it
E
1
R
2
L
K
2()
L
it
1()
L
it
2
R
3
R
1
L
E
2
C
2
i
1
i
3
R
1
R
3
i
K
1
2
L
5
▪Một số giả thiết đơn giản hóa:
-Các phần tử lý tưởng
-Động tác đóng mở lý tưởng
-Thời gian đóng mở bằng 0
-Luật Kirchhoff luôn đúng
Khái niệm quá trình quá độ
▪Mô hình toán học:
Hệ phương trình vi tích phân (Kirchhoff 1,2) + sơ kiện
