CHƯƠNG 3: L THUYẾT PHỤC VỤ
ĐÁM ĐÔNG
CHƯƠNG 3 L THUYẾTPHỤCVỤ ĐÁMĐÔNG
3.1. Khiniệmchung
Trong hoạt động sản xuất và đời sống thường nảy sinh tình huống mà một số đối
tượng đòi hỏi được phục vụ nhằm đáp ứng những yêu cầu nhất định nào đó (gi tắt
là các yêu cầu) mang tính chất tập hợp (số đông) và có tính ngẫu nhiên.
L thuyếtphụcvụ đmđông: Khoa học nghiên cứu giải quyết các vấn đề mà hệ
thống phục vụ đám đông đặt ra,lý thuyết phục vụ đám đông (hay còn gọi là lý thuyết
xếp hàng).
V dụ: Xe qua trạm thu ph, hê thống bốcdơ vậtliệutại công trường, công nhân vo
cng công trường,….
CHƯƠNG 3 L THUYẾTPHỤCVỤ ĐÁMĐÔNG
3.1. Khiniệmchung
dßng vµo
dßng vµo vÞ trÝ phôc vô
tõ chèi phôc vô
ra
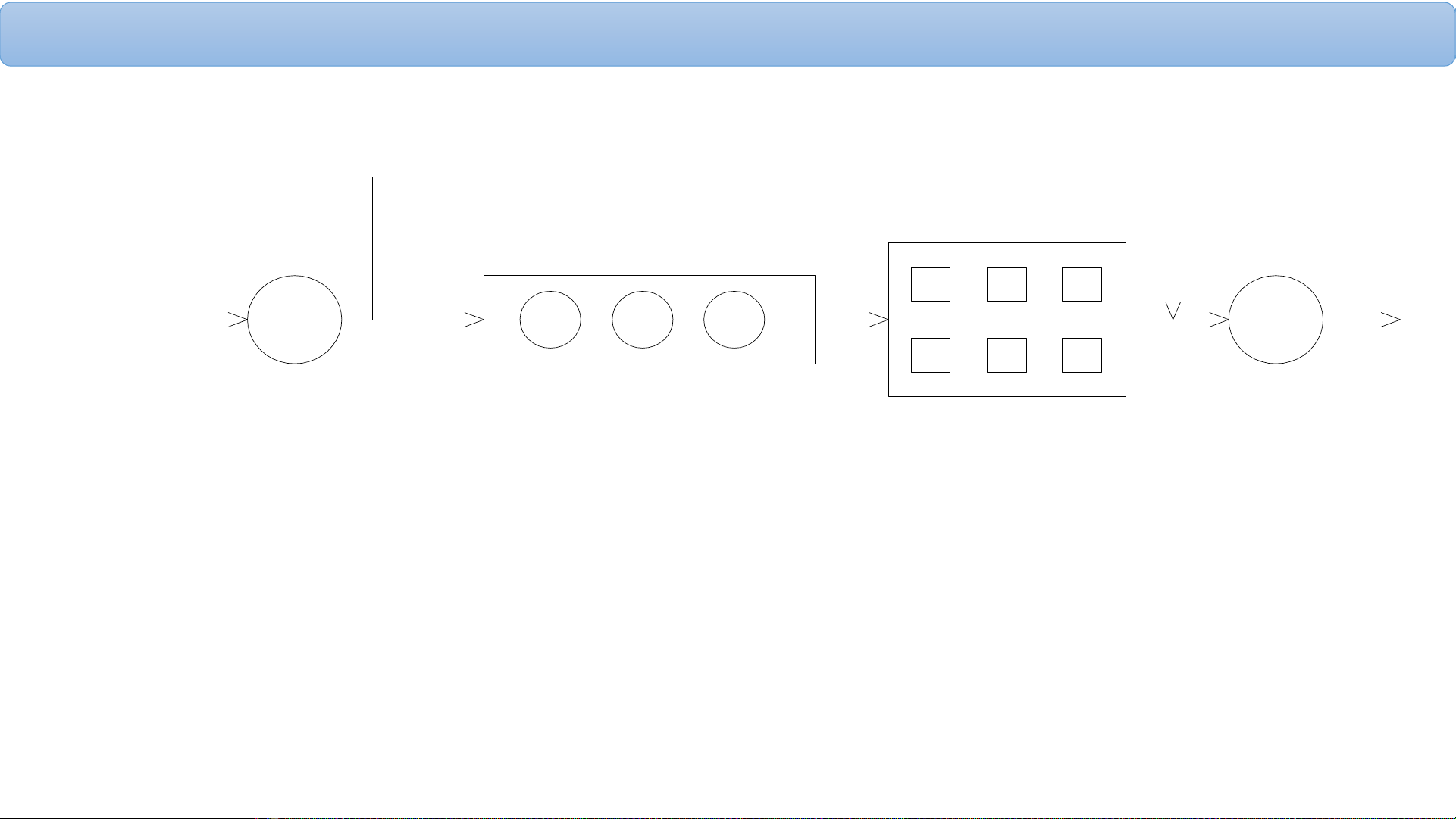
Hình: Cấu trúc chung của hệ thống phục vụ đám đông
- Dòng vào: dòng yêu cầu đến hệ thống phục vụ.
- Quá trình phục vụ: đặc trưng bởi khả năng đáp ứng các yêu cầu của dòng vào.
- Dòng ra: dòng yêu cầu đ được phục vụ hoặc dòng bị từ chối phục vụ.
- Khi một yêu cầu đến hệ thống phục vụ đám đông có 2 khả năng: Xếp hàng ><Từ chối
CHƯƠNG 3 L THUYẾTPHỤCVỤ ĐÁMĐÔNG
Định nghĩa: Là dòng các đối tượng đi đến hệ thống phục vụ đám đông đòi hỏi được
thỏa mãn một số yêu cầu nào đó.
Phân loi:
+ Theo nguồn yêu cầu: Gồm dòng hữu hạn và dòng vô hạn (dòng khách đến siêu thị,
dòng các phương tiện giao thông đi qua trạm soát vé,..là dòng vô hạn)
+ Theo số lượng yêu cầu: theo cá nhân hoặc theo nhóm (sinh viên đến thư viện là
dòng cá nhân, theo nhóm là các lô sản phẩm đến bộ phận kiểm tra chất lượng, các
gia đnh đến rạp hát,..)
+ Theo thời gian: theo 1 quy định giờ giấc hoặc ngẫu nhiên (dòng người đến các siêu
thị, trung tâm thương mại thường theo giờ giấc nhất định còn dòng các cuộc điện
thoại tới trung tâm là dòng ngẫu nhiên).
3.1.1. Dòng vào (dòng yêu cầu) của hệ thống
CHƯƠNG 3 L THUYẾTPHỤCVỤ ĐÁMĐÔNG
3.1.1. Dòng vào (dòng yêu cầu) của hệ thống
- Dòng yêu cầu đến hệ thống phục vụ đám đông là dòng các biến cố ngẫu nhiên.
- Trong phần ứng dụng này chỉ xét dòng vào là dòng phân phối Poisson.
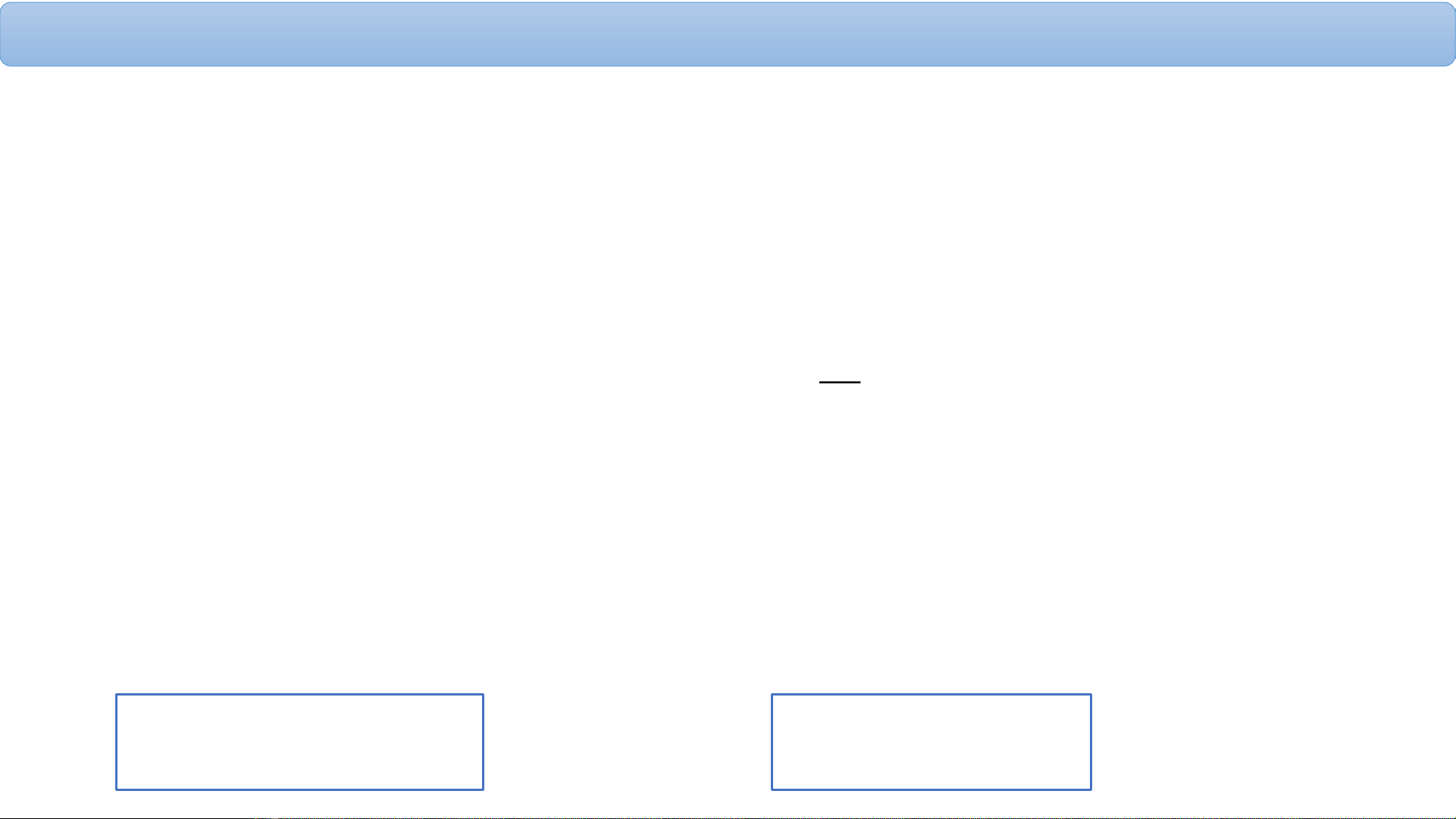
- Dòng Poisson tối giản: Xác suất trong 1 đơn vị thời gian t có k yêu cầu xuất hiện được
tính theo công thức:
Trong đó:
+ (k=0,1,..)
+ λ: là tham số biểu thị số yêu cầu xuất hiện trong một đơn vị thời gian t.
+ k: số yêu cầu xuất hiện tại thời điểm t.
-Mặt khác, nếu gọi Ƭlà khoảng thời gian giữa các lần xuất hiện các yêu cầu liên tiếp thì
Ƭlà đại lượng ngẫu nhiên tuân theo quy luật chỉ số (quy luật mũ):
k-λ
kk
λ
P (t)=P (λ)= e
k!
Hàm phân phối xác
suất có dạng:
F( ) 1 e
Hàm mật độ có
dạng:
f( ) e