PHƯƠNG PHÁP TÍNH
TOÁN TRONG KHOA HỌC
VÀ KỸTHUẬT VẬTLIỆU
Viện Khoa học và Kỹthuật Vật liệu
Đại học Bách khoa Hà Nội
Tính toán trên ký hiệu toán học
Các phép toán cơbản
D [f, x]
Tính
vi phân từng phần∂f/∂x
Intgrate
[f, x]
Tính
tích phân hàm f
Sum [f, {i, imin, imax
}]
Tính
tổng σ𝑖=𝑖𝑚𝑖𝑛
𝑖𝑚𝑎𝑥 𝑓
Solve [lhs == rhs, x
]
Gi
ảiphương trình cho ẩn x
Series
[f, {x, x0, order}]
Bi
ểudiễn dạng hàm mũ củaf đối vớ
i
đi
ểmx=x0
Limit[f, x -
> x0]
Tìm
giới hạn𝐿𝑖𝑚𝑥→𝑥0𝑓
Minimize [f, x]
C
ựctiểu của hàm f đối vớibiến x
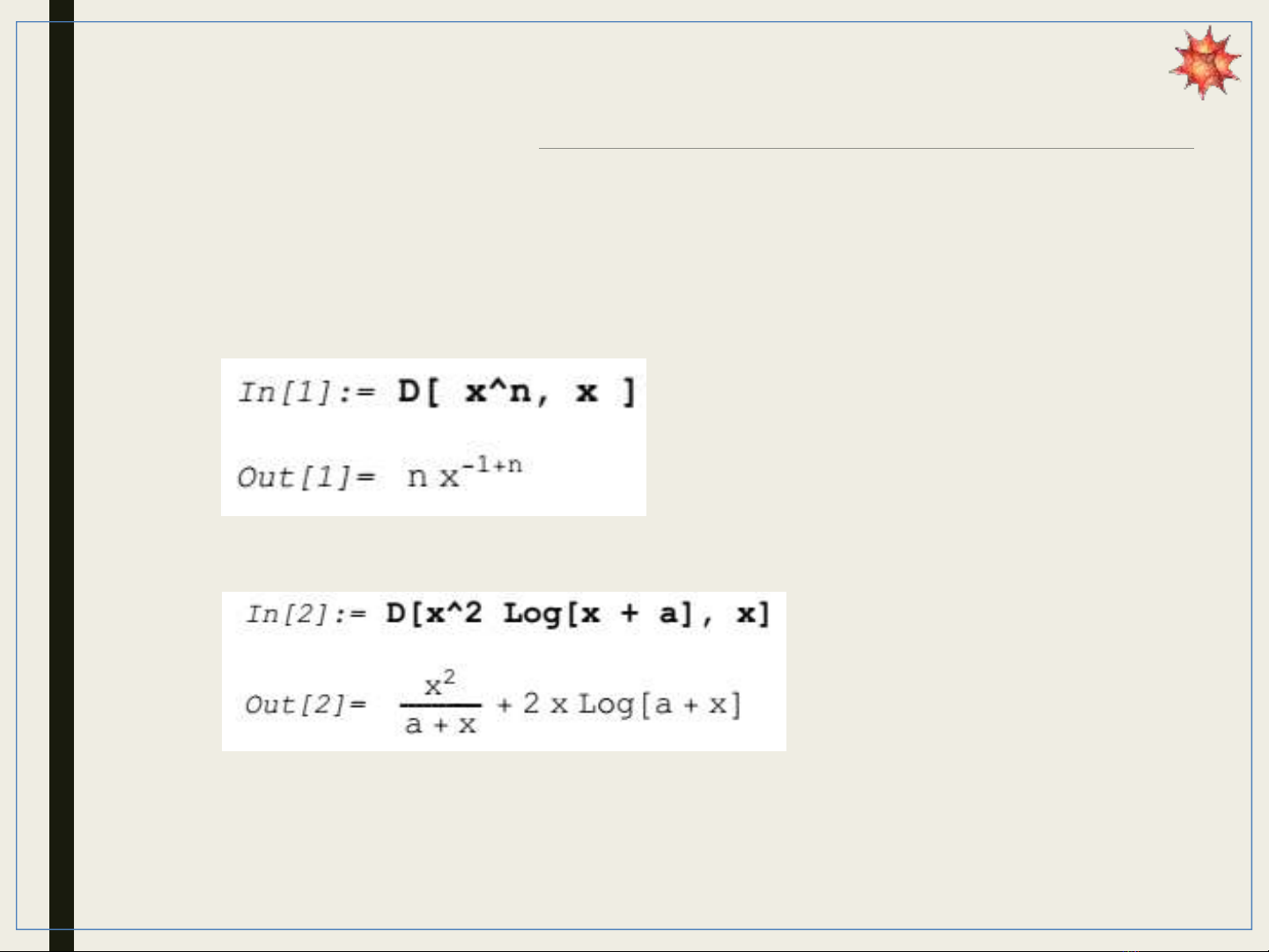
Ví dụ: Tính vi phân từng phần của 1 hàm số
Tính toán trên ký hiệu toán học
D [f, x1, x2, …
]
Tính
vi phân từng phần hàm nhiề
u
bi
ến
D [f, {x, n}]
Tính
vi phân từng phần bậc n
Dt [ f ]
Tính
vi phân toàn phầndf
Dt [f, x]
Tính
vi phân toàn phầndf/dx
Tính vi phân của 1 hàm số
Tính toán trên ký hiệu toán học
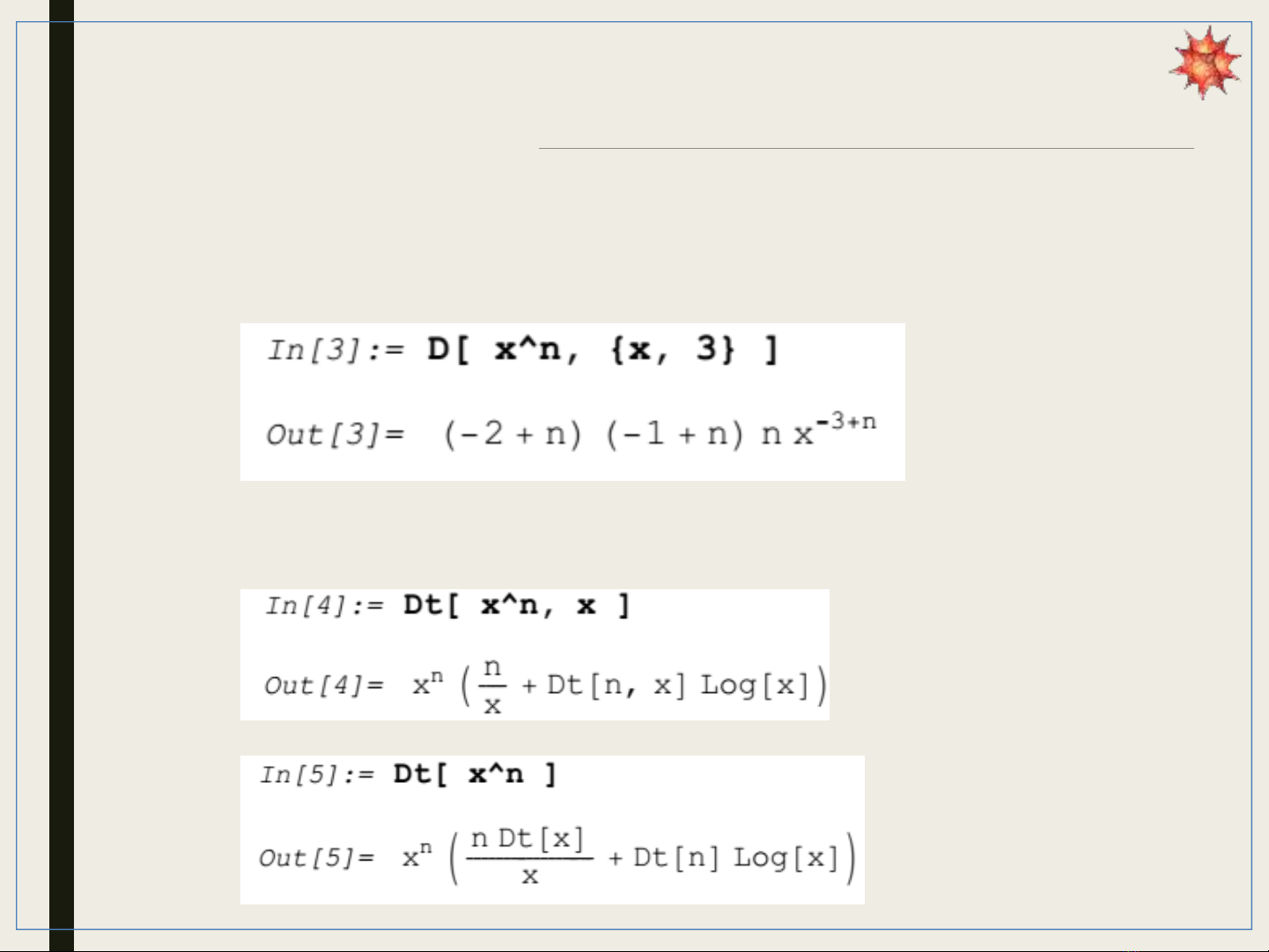
Ví dụ: Tính vi phân toàn phầncủa1 hàm số
Ví dụ: Tính vi phân từng phần bậc cao của1 hàm số
Tính toán trên ký hiệu toán học