SEMINAR KHOA HC
TP M-THÔ V NG DNG TRONG KHAI PH D LIU
PGS. TS. HÀ QUANG THỤY
HÀ NỘI 11-2016
TRƯNG ĐẠI HC CÔNG NGH
ĐẠI HỌC QUỐC GIA HÀ NỘI
1
Nội dung
1. Tp thô
2. Tp mờ
3. Tp mơ-thô
4. Tp mơ-thô vi la chn đc trưng
5. Tp mơ-thô vi phân lp
6. Tp mơ-thô vi phân lp đa nhn
2
1. Tp thô
⚫ngha ca tp thô
▪Biu din mt tnh cht ca cc đi tưng m nhn thc r mt
đi tưng c tnh cht đ song không đ thông tin đ nhn thc
(mô t) r rng v tnh cht đ. Con người thng nht đnh gi v
tnh cht đo c trong mi đi tưng song không đ thông tin mô t
đưc tnh cht đ
▪V d: Tnh cht “b mt bnh” no đ: thông tin hin c qua xt
nghim cho bit cng mt kt qu xt nghim song c người b
bnh, c người không b bnh.Nhn thc r rng v người b
bnh/người không b bnh
▪Tp thô thc cht l tp theo quan nim thông thưng
⚫Xut xư l lch s pht trin
▪Zdzislaw I. Pawlak 1981-1982, sau đ đưc cng đng pht trin
▪1926-2006
3
Tp thô: Nghiên cu v ng dng
⚫http://www.sciencedirect.com :
▪5000+ bi bo ~ "rough set"
▪60+ bi bo ~ "rough reduction"
▪30+ bi bo ~ “rough classifier“
▪150+ bi bo ~ “rough cluster“
▪280+ bi bo ~ "rough pattern“
⚫Tnh ton ht
▪Granular computing (GrC). Tp thô v tp mờ phbin
▪Mô hnh x l thông tin mi ni: nghiên cu đa ngnh vi mc tiêu
đ kho st v mô hnh cch tư duy, mt h cc phương php gii
bi ton đnh hưng tnh ton ht, v mt giai đon x l thông
tin. Tnh ton ht nghiên cu mt l thuyt chung gii bi ton da
trên cc mc khc nhau ca ht v c th.
▪Rule representation/interpretation; Rule mining; Combination with
other methods;
▪Khung KPDL theo tnh ton ht: Knowledge granule (mu tri thc),
tri thc cu trc ha (Structural knowledge), thut ton khai ph
4
Yiyu Yao. Granular computing for data mining. Data Mining, Intrusion Detection,
Information Assurance, and Data Networks Security 2006:624105
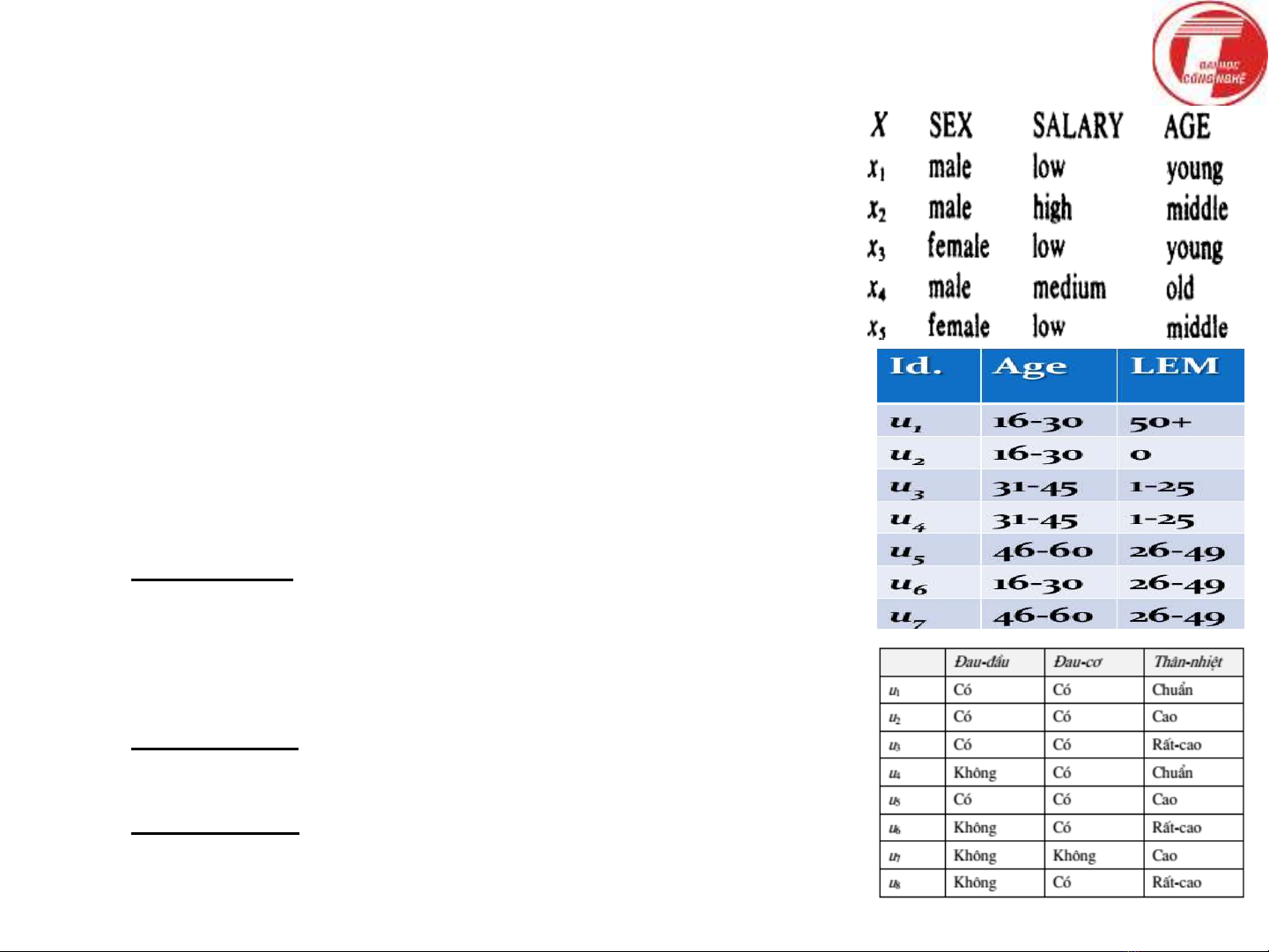
H thông tin
⚫H thông tin
▪H thông tin S=<U, A, V, >
▪Tp U khc rng cc đi tưng. V d,
U={x1, x2, x3, x4, x5}
▪Tp A khc rng cc thuc tnh. V d,
A={SEX, SALARY, AGE}
▪V tp cc gitr, V={VsexVsal Vage}
▪: UA→V; aAxU đt a(x)=(x,a)
⚫V d h thông tin
▪Bng trên. Salary = “low”l dưi $6000
năm,“medium”l t $6000 ti $24000
năm,“high”trên $24000. Age : cc đ tui
<21; [21,40], 40<. Sex(x5)=female …
▪Bng gia mt v d khc: 7 hc viên vi
cc cc đ tui v ch s luyn
▪Bng dưi: tnh trng ca 8 bnh nhân vi
đau-đu, đau-cơ v thân nhit. Gitr thuc
tnh thân nhit theo quy đnh ngnh y t. 5