Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 299
Chương 12: Phép biến đổi bảo giác
12.1 Biểu diễn hình học của hàm biến phức.
12.2 Phép biến đổi w = z2 và w = zn.
12.3 Phép biến đổi w = ez.
12.4 Phép biến đổi bảo giác.
12.5 Phép biến đổi Mobius.
12.6 Phép biến đổi Mobius biến (z1, z2, z3) thành (w1, w2, w3).
12.7 Biến nửa mặt phẳng trên thành đĩa đơn vị.
12.8 Tìm phép biến đổi biến thành ’.
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 300
12.1 Biểu diễn hình học của hàm biến phức
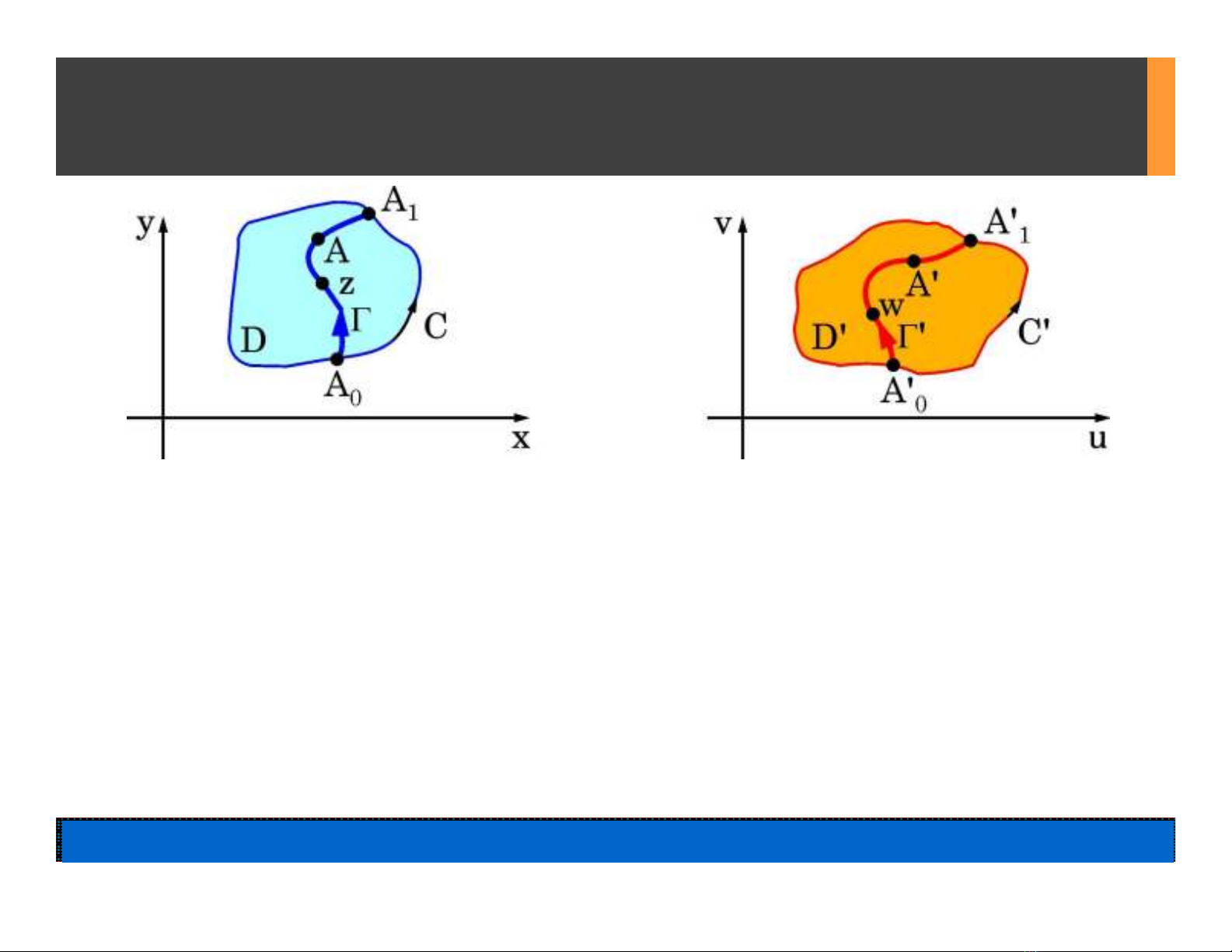
Mặt phẳng z (x, y, r, q, Q, z, Mặt phẳng w (u, v, r, f, F, w,
H12.1(a) H12.1(b)
z)
w)
(Số phức z Số phức w)
Điểm A Điểm A'
Chu tuyến C Chu tuyến C'
(Điểm z Điểm w)
Đường Đường '
Miền D Miền D'
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 301
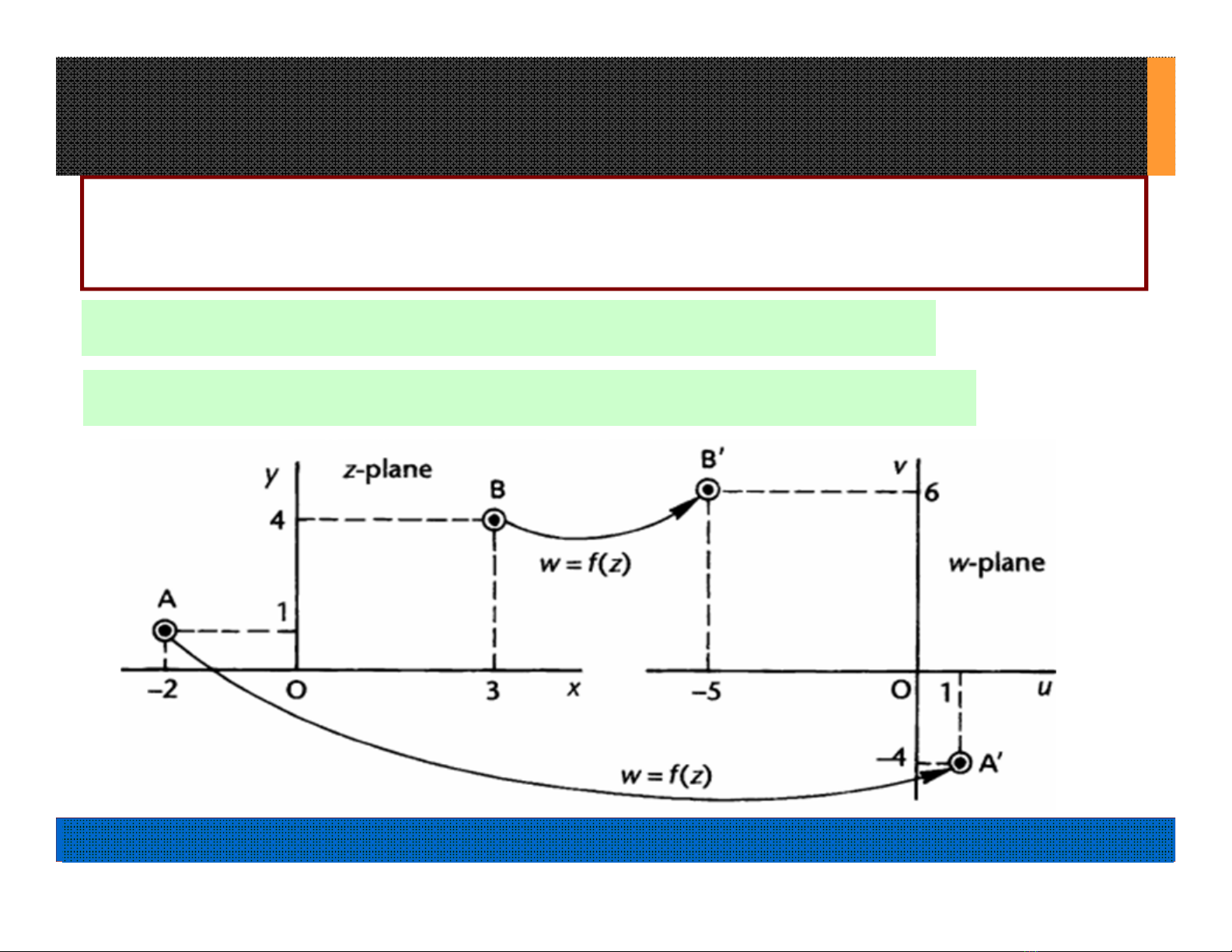
VD 12.1.1: Biểu diễn hình học của hàm phức
Tìm ảnh của các điểm A(z = –2 + i) và B(z = 3 + 4i) thông qua
phép biến đổi w = 2iz + 3 ? Minh họa trên mặt phẳng phức ?
Điểm A(z = -2 + i) A’(w = 2i(-2 + i) + 3 = 1 –4i )
Điểm B(z = 3 + 4i) B’(w = 2i(3 + 4i) + 3 = –5 + 6i )
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 302
12.2 Phép biến đổi w = z2
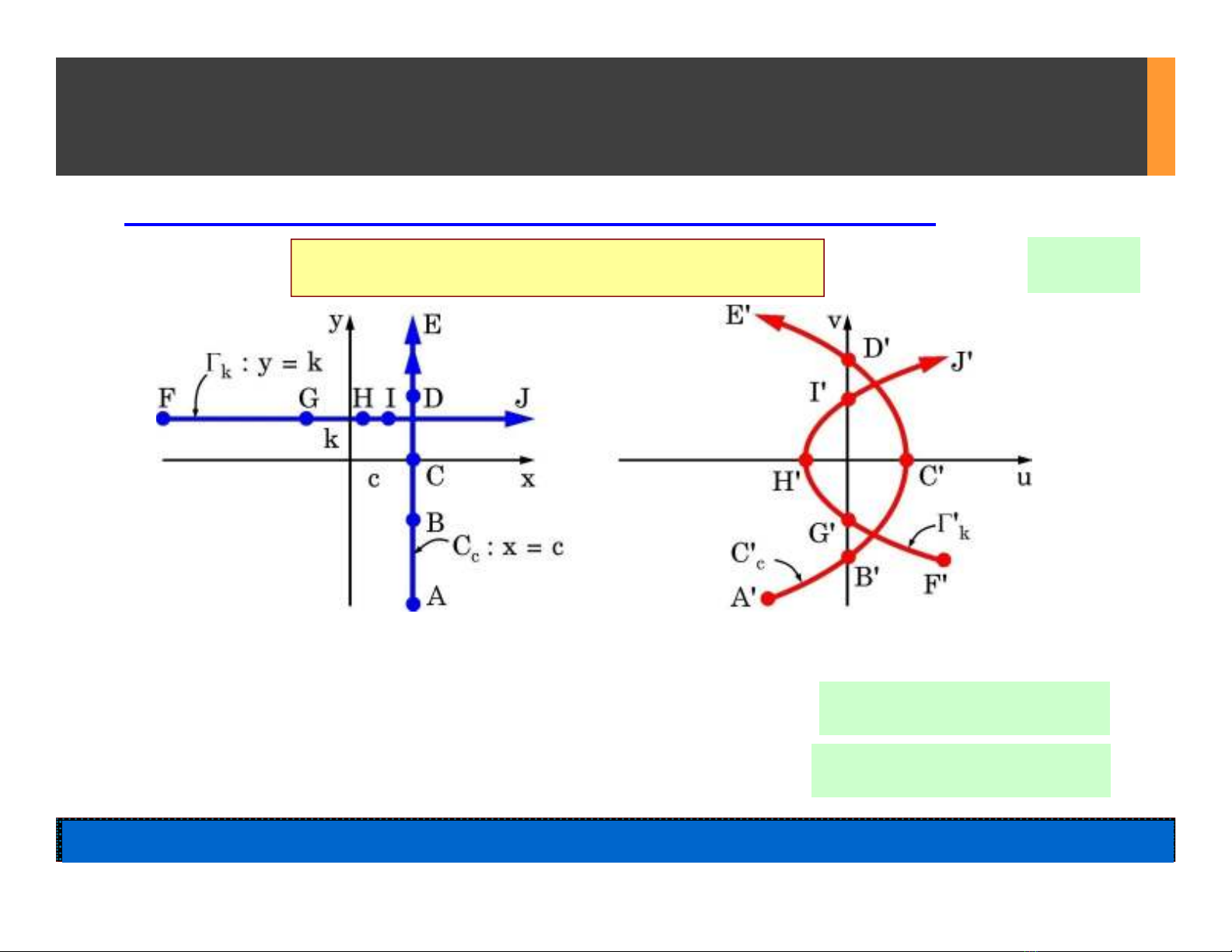
1. Khảo sát trong Tọa Độ Vuông Góc (H12.2 và 12.3):
(12.1)
2 2 2
w z u x y ; v 2xy
H12.2(a) H12.2(b)
Họ Đường Tọa Độ Cc: x = c Họ Parabôn
'
2 2 2
c
Họ Đường Tọa Độ k: y = k Họ Parabôn
:
'
2 2 2
k
u v /4c c
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 303
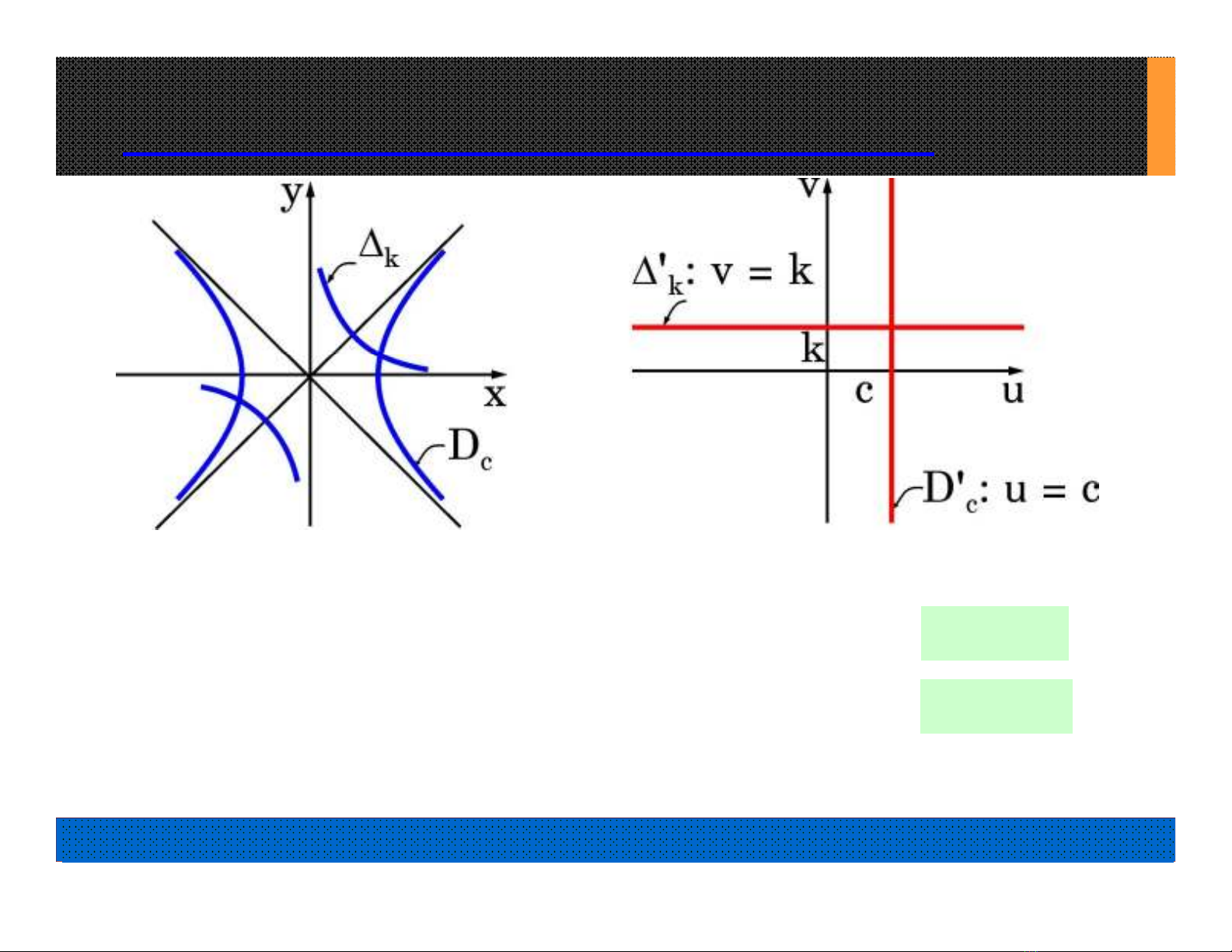
1. Khảo sát trong Tọa Độ Vuông Góc (H12.2 và 12.3): (tiếp theo)
H12.3(a) H12.3(b)
Họ Hypebôn Dc: x2 – y2= c Họ Đường Tọa Độ
c
D u c
'
:
Họ Hypebôn k: 2xy = k Họ Đường Tọa Độ
k
v k
'
:
với mọi c và mọi k.
c k c k
C vaøD ,
' '