34
%
34
%
13.5
%
13.5
%
2.5
%m+
m-
m- 2
2.5
%
mm+ 2
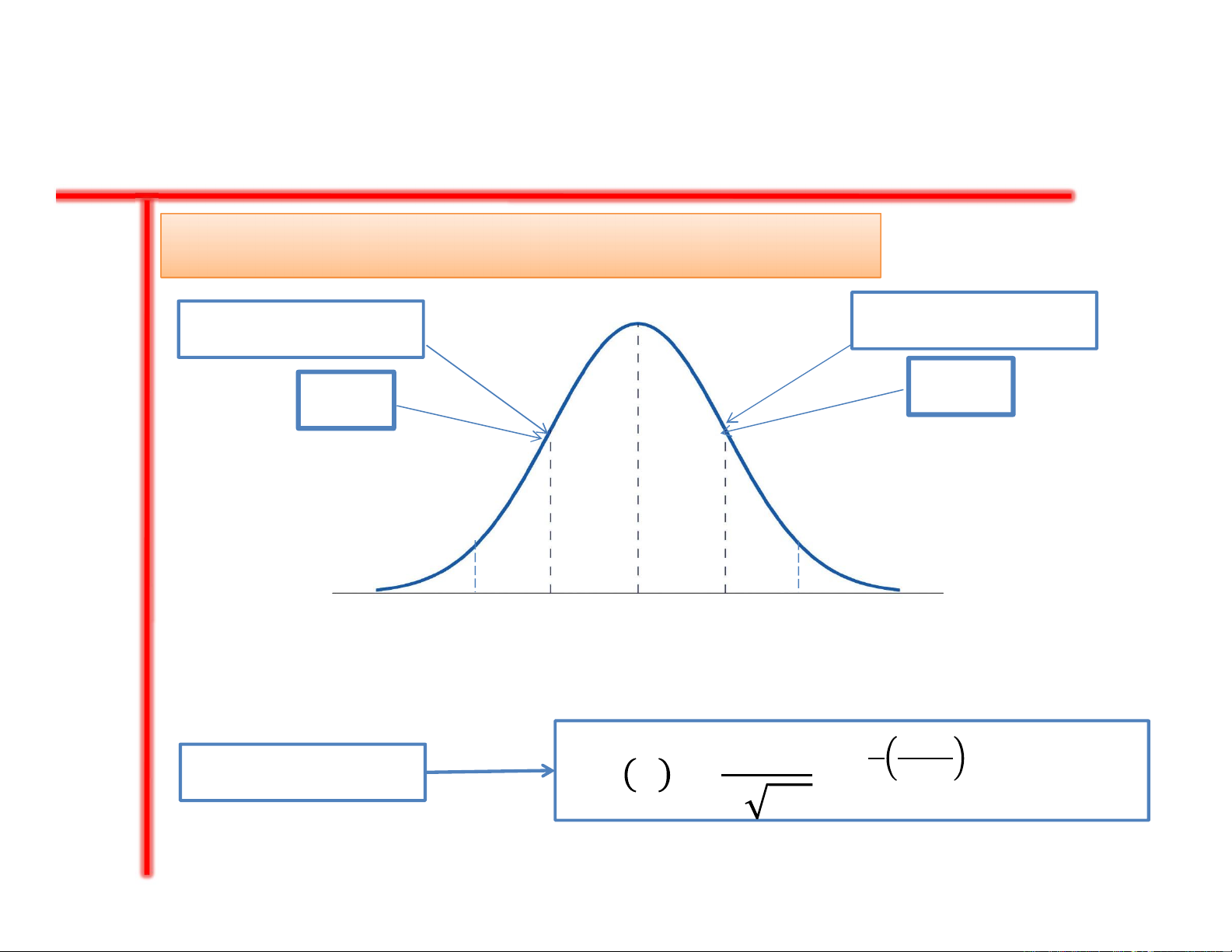
Chương 2: CÁC HÀM PHÂN BỐ
1.1. Hàm Gauss (normal distribution)
Công thức
Điểm uốn
Điểm uốn
= 1
2
[

] (2.1)
m-m+
Với z = ()
Định luật Giới hạn trung tâm (Central limit theorem)
⁃Với một tập hợp có giá trị trung bình μ và độ lệch chuẩn σ.
⁃Nếu lấy các mẫu với kích thước mẫu đủ lớn từ tập hợp trên (n
>30)
⁃Phân bố của các trung bình mẫu là phân bố chuẩn với σ =
hay z = ()
/
(*)
⁃: độ lệch chuẩn tổng thể
- Nếu tập hợp có phân bố chuẩn thì (*) đúng với cả trường hợp
mẫu nhỏ
- Biết , z và
®xác định
−= z
(*)
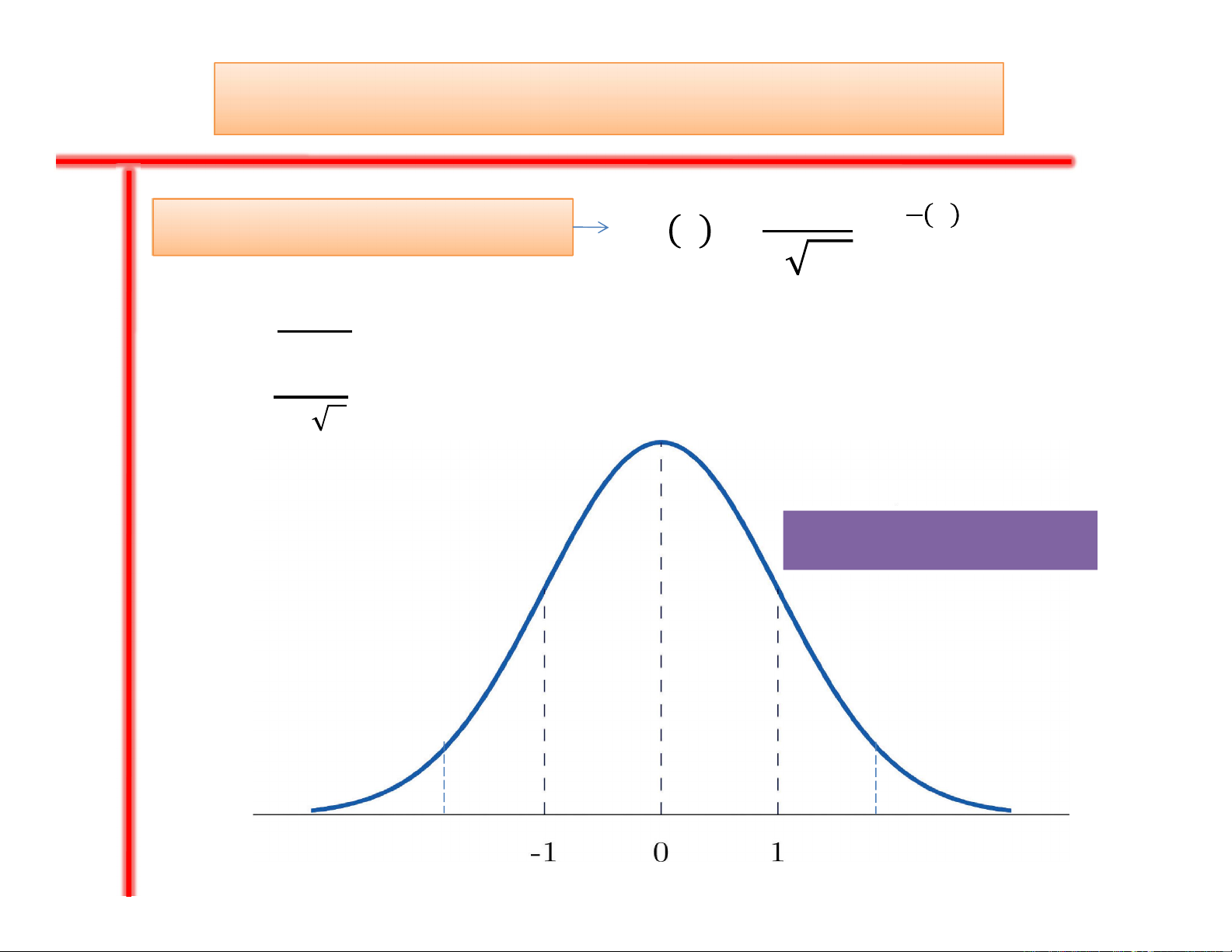
2.1. Hàm Gauss chuẩn hóa
Hàm Gauss chuẩn hoá
0.34 0.34
0.135
2
-2
0.135
0.025 0.025
µ= 0 và σ= 1
Với z = ()
hay
z = (
)
/
®(z score)
: độ lệch chuẩn tổng thể
f z = 1
2π
e[
] (2.2)
Đặc
điểm Hàm Gauss Hàm Gauss chuẩn hoá
Kỳ vọng mx; có thứ nguyên của x m
: không thứ nguyên
Phương
sai
x2 và x: có thứ nguyên
của x
= 1và = 1: không
thứ nguyên
Dạng
hình
Đối xứng hình chuông, có 2
điểm uốn tại x = ±x
Đối xứng hình chuông,
có 2 điểm uốn tại z = ± 1
Số lần
thực
nghiệm
n là , (thường chấp nhận n >30)
So sánh hàm Gauss và Gauss chuẩn hoá
2.1. Hàm Gauss
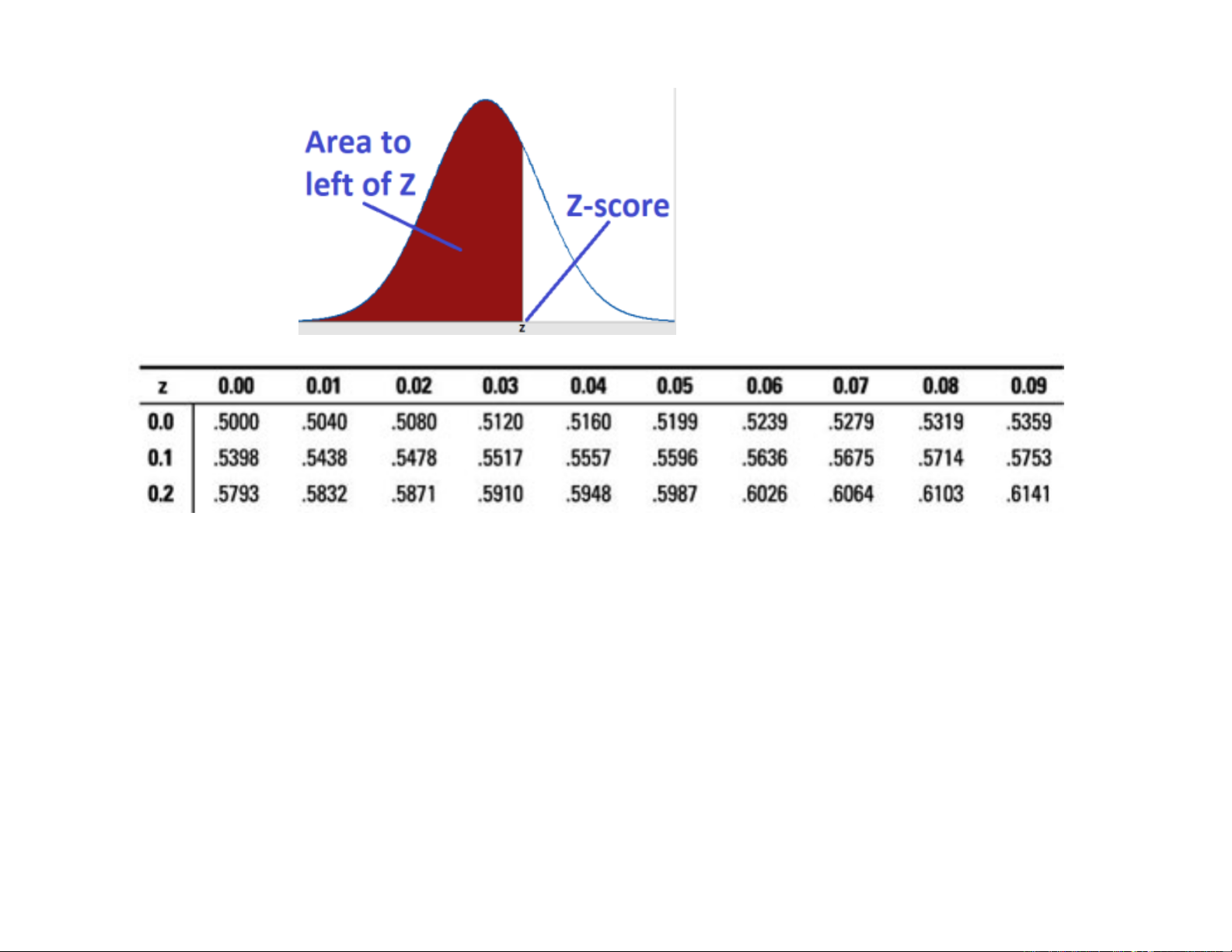
Mô tả bảng phân vị z:
- Giá trị phân vị z nằm ở cột đầu và hàng đầu của bảng phân vị.
+ Cột đầu: phần phân vị z với 1 chữ số sau dấu phẩy
+ Hàng đầu: chữ số thứ 2 sau dấu phẩy của giá trị z
- Giá trị bên trong bảng cho ta tỉ lệ của diện tích khu vực bên trái (tô
đỏ) hay là xác xuất để phân vị Z z