Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 268
Chương 10: Lý thuyết thặng dư
10.1 Phân loại các điểm bất thường.
10.2 Thặng dư.
10.3 Định lý thặng dư.
10.4 Thặng dư tại cực.
10.5 Zero cấp m.
10.6 Quan hệ giữa zero cấp m và cực cấp m.
10.7 Cực đơn của P(z)/Q(z).
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 269
10.1 Phân loại các điểm bất thường:
1. Điểm bất thường cô lập (H10.1):
z1, z2, … = Điểm bất thường của f(z).
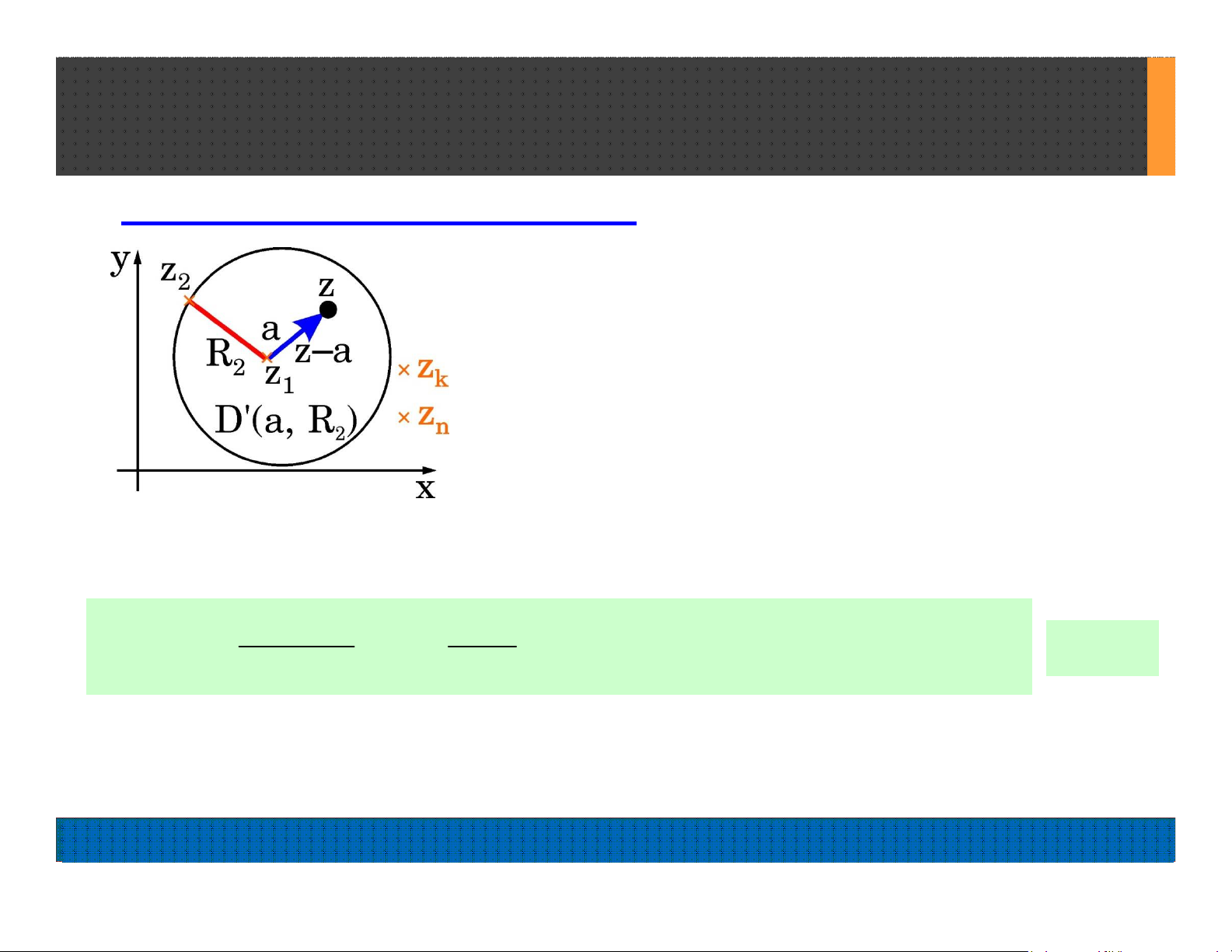
Nếu có D(z1, r) sao cho trong D
không có Điểm bất thường nào khác
thì z1 là Điểm bất thường cô lập của
f(z).
f(z) được khai triển thành chuổi Laurent quanh a = z1.
(10.1)
n
m 1 o 1 n
m
a a
f(z) a a (z a) a (z a)
z a
(z a)
(10.1) có giá trị trong Đĩa hở vô tâm D'(a, R2) với
R2= |z – a| là Khoảng cách từ a đến Điểm bất thường gần a nhất.
H10.1
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 270
2. Cực cấp m (bậc m):
a = cực của f(z) nếu (10.1) chỉ chứa 1 số hữu hạnLũy thừa âm.
a = cực cấp m của f(z) nếu m là Lũy thừa âm cao nhất.
Phần chính của f(z) quanh cực a cấp m :
(10.2)
m 2 1
m 2
a a a
g(z)
z a
(z a) (z a)
3. Điểm bất thường chủ yếu: a là Điểm bất thường chủ yếu của
f(z) nếu (10.1) chứavô số Lũy thừa âm.
4. Điểm bất thường khử (bỏ) được: a là Điểm bất thường khử
được của f(z) nếu (10.1) không chứa Lũy thừa âm.
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 271
VD 10.1.1: Phân loại điểm bất thường
Chỉ ra các điểm bất thường và cho biết loại của chúng :
2
3
z
(z 1)
a)
3
22z z 1
(z 4) (z j)(z 1 2j)
b)
2
sin(mz)
(z 2z 2)
c)
1 cosz
z
d)
a) z = -1 : cực bậc 3.
b) z = 4: cực bậc 2; z = j và 1 – 2j : cực đơn.
c) z = – 1 + j và – 1– j : cực đơn.
d) z = 0 : điểm bất thường khử được .
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 272
10.2 Thặng dư:
1. Định nghĩa:
a = Điểm bất thường của f(z).
(10.1) là khai triển Laurent của f(z) trong cận D’(a, R2).
a–1 gọi là Thặng dư của f(z) tạiĐiểm bất thường a.
(10.3)
1
a Res f(z); a
2. Tính Tích Phân Chu Tuyến Bằng Thặng Dư:
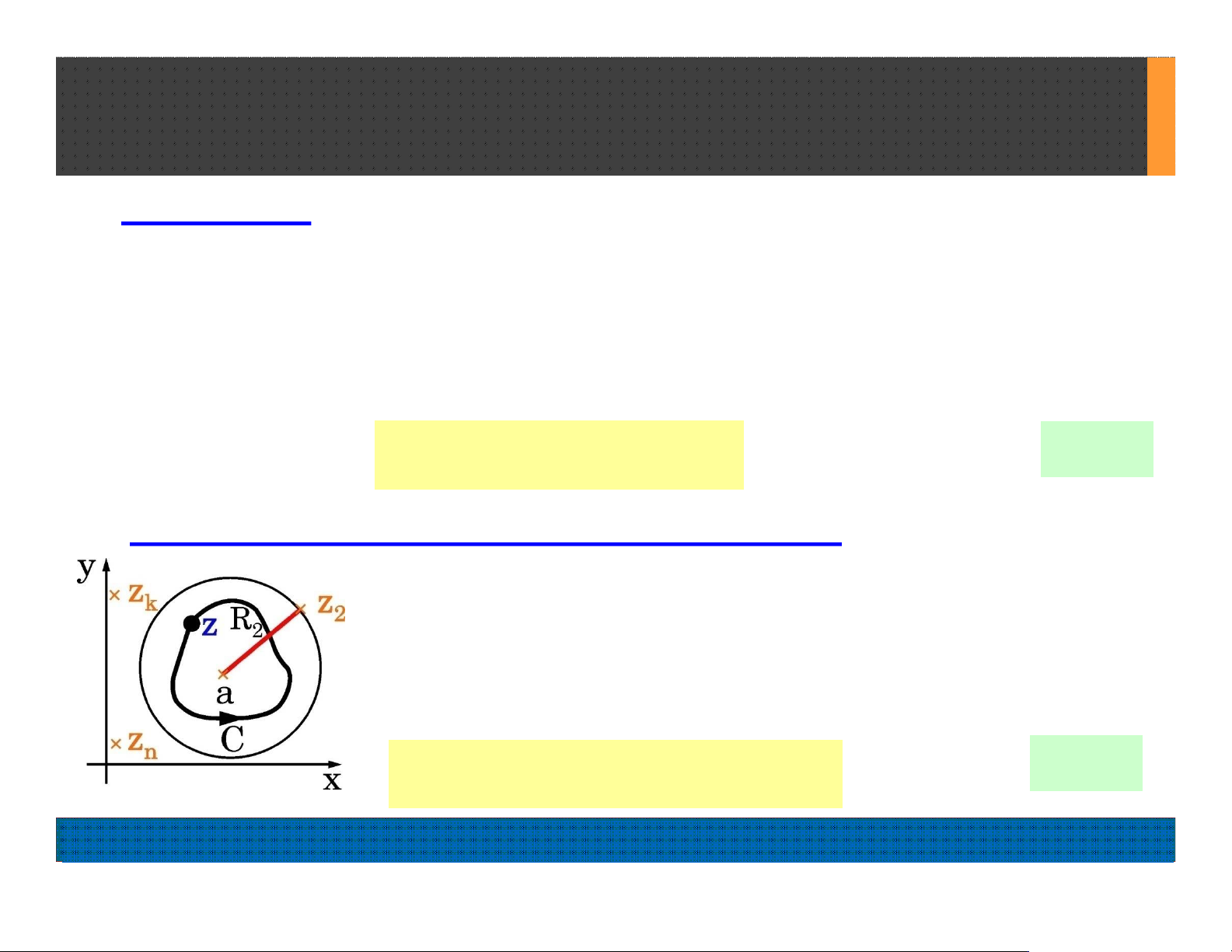
°a=Điểm bất thường của f(z) (H10.2).
°C = D'(a, R2) đường kín đơn bao quanh a.
! Trong (9.31), lấy n = –1 rồi thay bởi z:
H10.2
C
f(z)dz 2 iRes f(z); a
(10.4)