Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 213
Chương 8: Tích phân phức
8.1 Tích phân đường phức.
8.2 Tích phân đường thực không phụ thuộc đường đi.
8.3 Định lý Cauchy và các hệ quả.
8.4 Công thức tích phân Cauchy và các hệ quả.
8.5 Công thức tích phân Poisson.
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 214
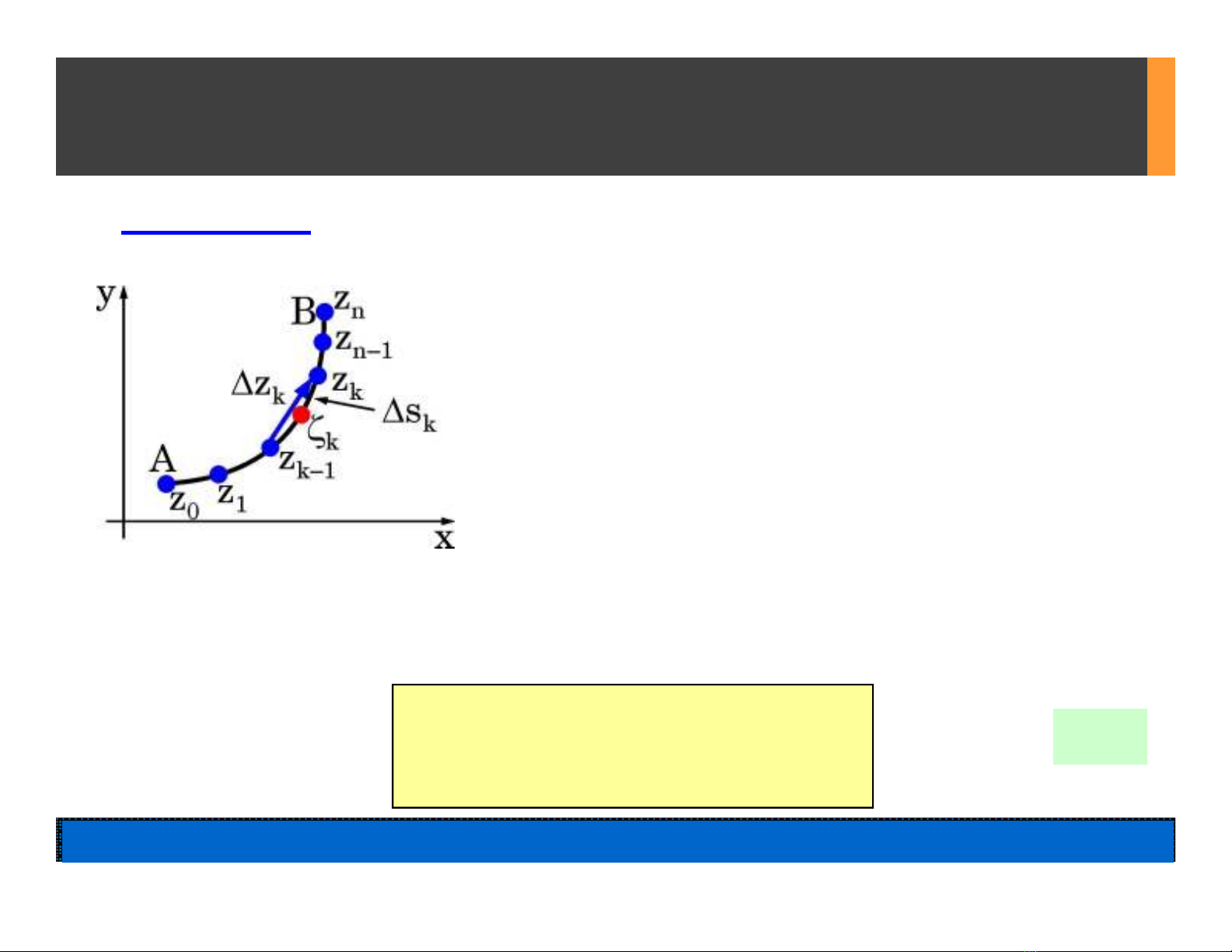
8.1 Tích phân đường phức:
°A, B = hai điểm trong miền D
°Cung trơn từng đoạn
° sự phân chia C
°= dây cung
°= cung
°
°f(z) = hàm liên tục trong D
฀
C AB
k
z 1
z z z
฀
k k 1 k
s z z
k k k k
i ñieåm treân s
D
1. Định nghĩa:
H8.1
Tích phân đường phức của f(z) dọc theo C, từ A đến B, là:
(8.1)
1
n
k k
nk
C
f (z)dz lim f ( ) z
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 215
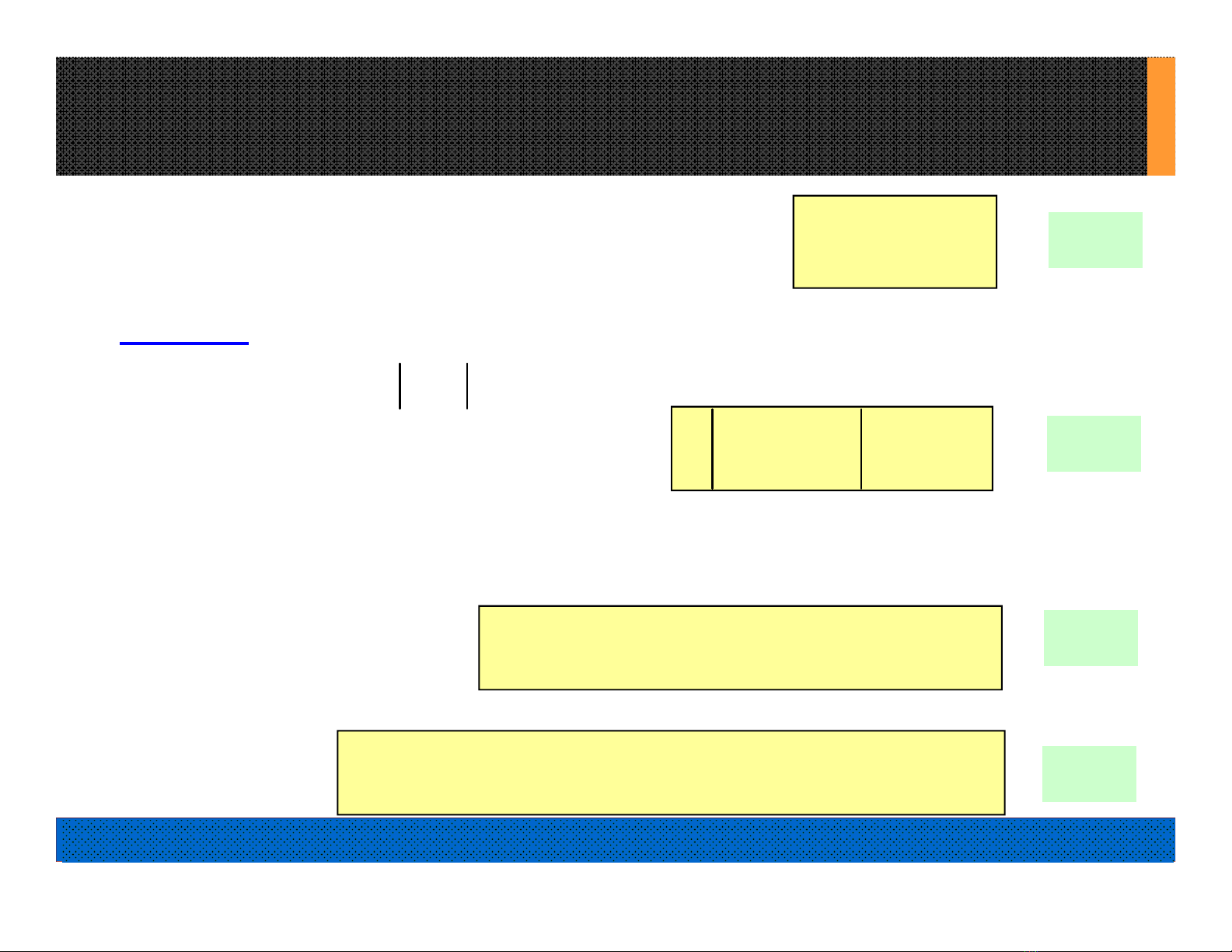
8.1 Tích phân đường phức: (tiếp theo)
(8.2)
Nếu A B, C là Đường kín, ta có Tích
phân chu tuyến:
C
f(z)dz
฀
2. Định lý: (Về chặn trên của tích phân đường phức)
3. Cách tính tích phân đường phức:
°f(z) LT trên C; ; L là chiều dài của C:
f (z) M, z C
C
f(z)dz ML
(8.3)
°C cho bởi PT Thông số z(t) = x(t) + iy(t); tot t1
1
0
t
C t
f(z)dz f z(t) z'(t)dt
(8.4)
f(z) u(x,y) iv(x,y)
°
C C C
f(z)dz udx vdy i vdx udy
(8.5)
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 216
4. Tính chất của tích phân đường phức:
(8.6)
1 0
0 1
z z
z z
f(z)dz f(z)dz
●
(8.7)
1 1
0 0
z z
z z
kf(z)dz k f(z)dz
●
(8.8)
1 1 1
0 0 0
z z z
z z z
f(z) g(z) dz f(z)dz g(z)dz
●
(8.9)
1 2 1
0 0 2
z z z
z z z
f(z)dz f(z)dz f(z)dz
●
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 217
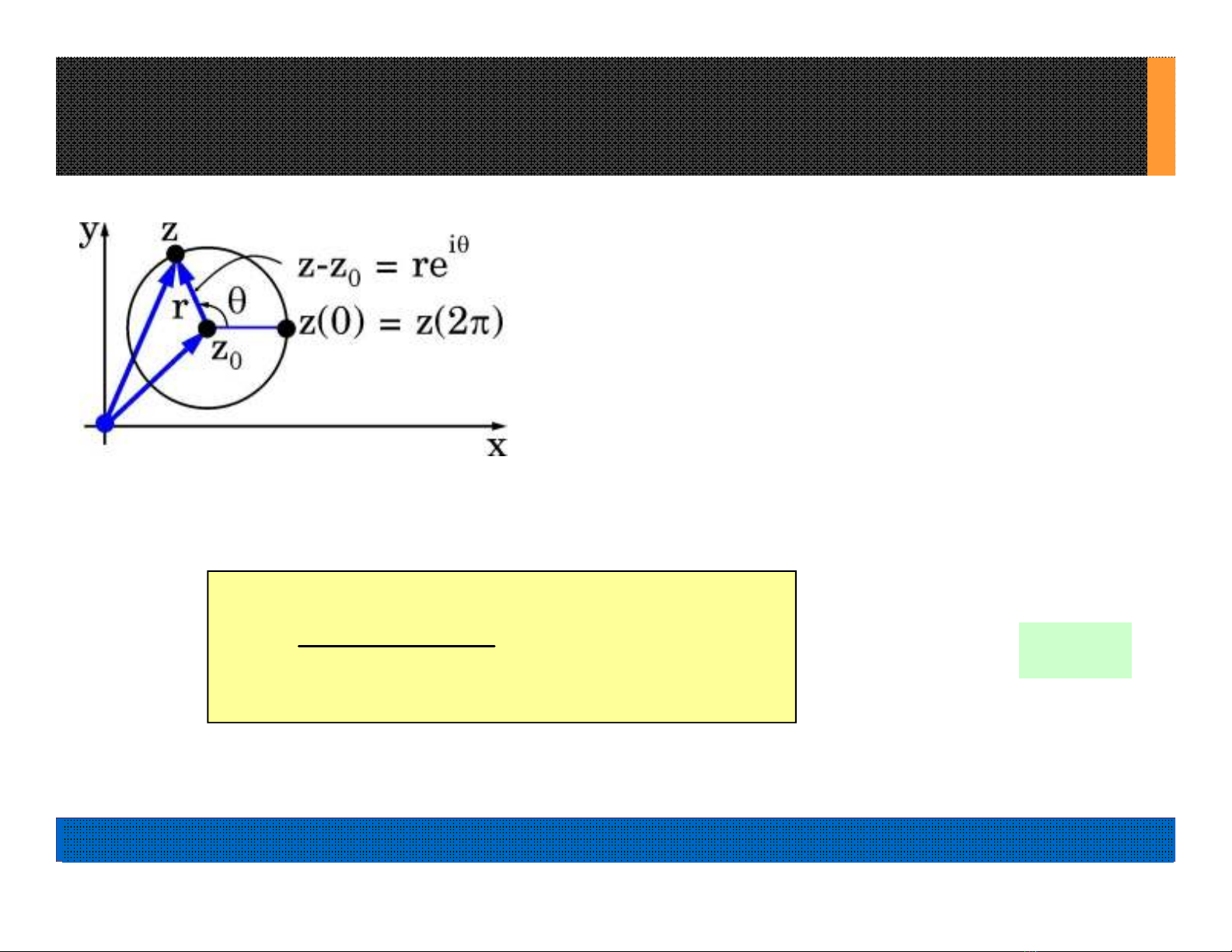
5. Ví dụ quan trọng: (H 8.2)
(8.10)
n 1
C
0
2 i (n 0)
dz
0 (n 0)
(z z )
฀
C = vòng tròn C (zo,r)
H8.2