Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 235
Chương 9: Chuổi hàm phức
9.1 Định nghĩa.
9.2 Các điều kiện hội tụ của chuổi hàm phức.
9.3 Vài tính chất của chuổi hội tụ.
9.4 Chuổi hàm phức hội tụ đều.
9.5 Các tính chất của chuổi hàm phức hội tụ đều.
9.6 Chuổi lũy thừa.
9.7 Chuổi Taylor.
9.8 Cách tìm chuổi MacLaurin và Chuổi Taylor.
9.9 Chuổi Laurent.
9.10 Cách tìm chuổi Laurent.
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 236
9.1 Định nghĩa:
1. Hội tụ (HT), Phân kỳ (PK), Miền hội tụ (MHT):
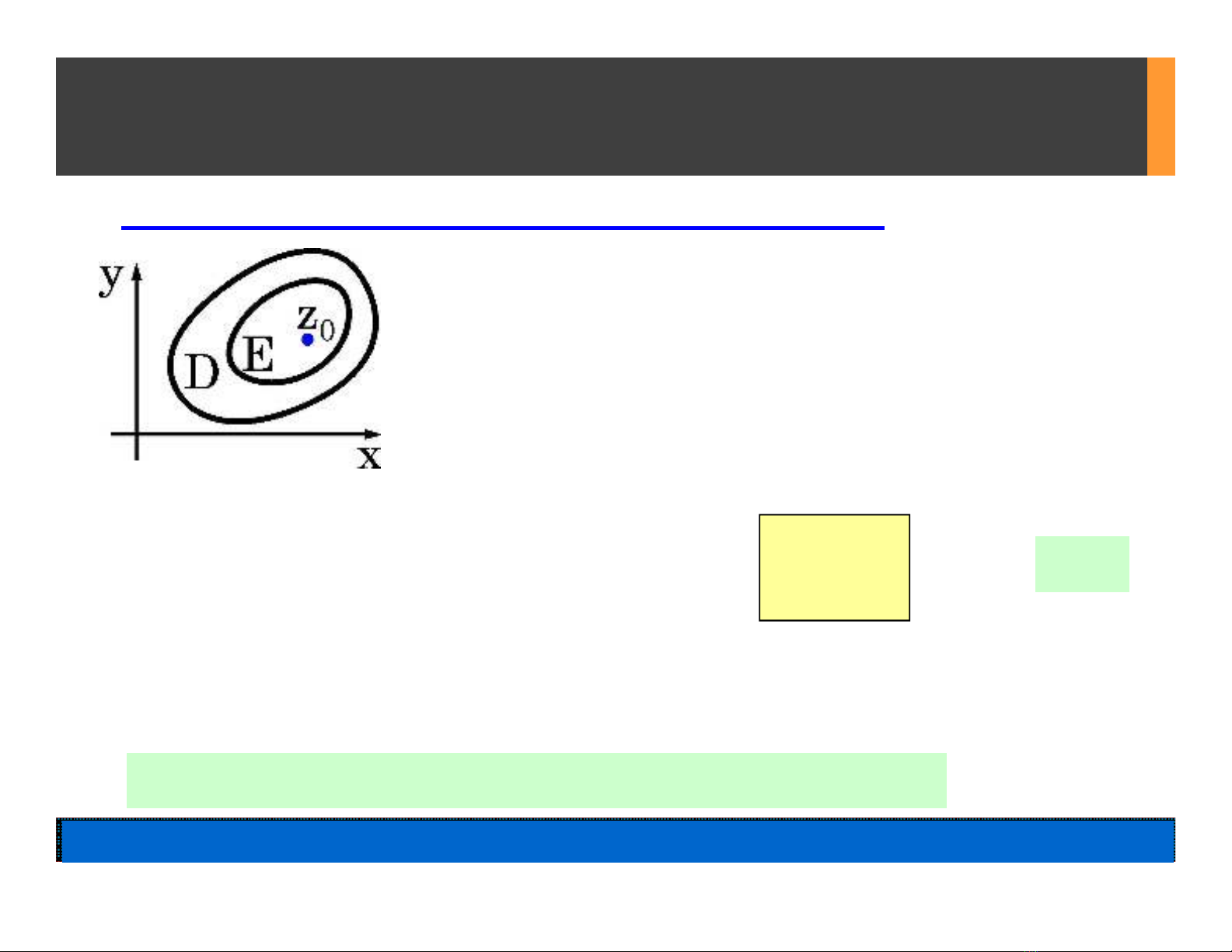
°D = 1 miền (H9.1)
°dãy HP xác định trên D
°
°=Dãy tổng riêng
n
f (z) 1
n 1 n
S (z) f (z) f (z); n 1,2,...
n
S (z)
H9.1
(9.1)
n
n 1
f (z)
Cố định z0D. Chuổi Hàm Phức (HP):
nếu Dãy số phức hội tụ về số phứcS(z0):
n 0
S (z )
0 0 n 0
0, N( ,z ) :|S(z ) S (z )| n N
Hội tụ (Đơn) tại z0 về Tổng S(z0),
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 237
9.1 Định nghĩa: (tiếp theo)
2. Hội tụ tuyệt đối (HTTĐ): Xét chuổi số thực dương:
Chuổi (9.1) PK tại z0 nếuDãy số phức PK.
n 0
S (z )
Miền Hội Tụ (Đơn) của (9.1) là:
(9.2)
09 1
E z D :( . ) Hoäi Tuï(Ñôn)
S(z) = f(z) là Hàm Tổng của (9.1), xác định trong E.
Chuổi (9.1) HTTĐ tại z0 nếu Chuổi (9.3) HT.
n n n
n n
f (z ) u (x , y ) v (x , y )
2 2
0 0 0 0 0
1 1
(9.3)
3. Bán hội tụ (BHT - hội tụ có điều kiện): Chuổi (9.1) BHT nếu
(9.1) HT nhưng (9.3) PK.
! Nếu (9.3) HT thì (9.1) HT.
! Nếu 1 Chuổi HP Hội tụ tuyệt đốithì Hội tụ.
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 238
9.2 Các điều kiện hội tụ của chuổi hàm phức:
1. Hội tụ của chuổi phần thực và chuổi phần ảo:
Và xét hai chuổi hàm thực của hai biến thực:
! (9.1) hội tụ (9.5) hội tụ. Lúc đó, nếu đặt:
(9.4)
Đặt:
n n n
f (z) u (x,y) iv (x,y)
1 1
n n
n n
u (x,y) vaø v (x,y)
(9.5)
1 1
n n
n n
u (x,y) u(x,y) vaø v (x,y) v(x,y)
(9.6)
thì :
n
n 1
f (z) f(z) u(x,y) iv(x,y)
(9.7)
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 239
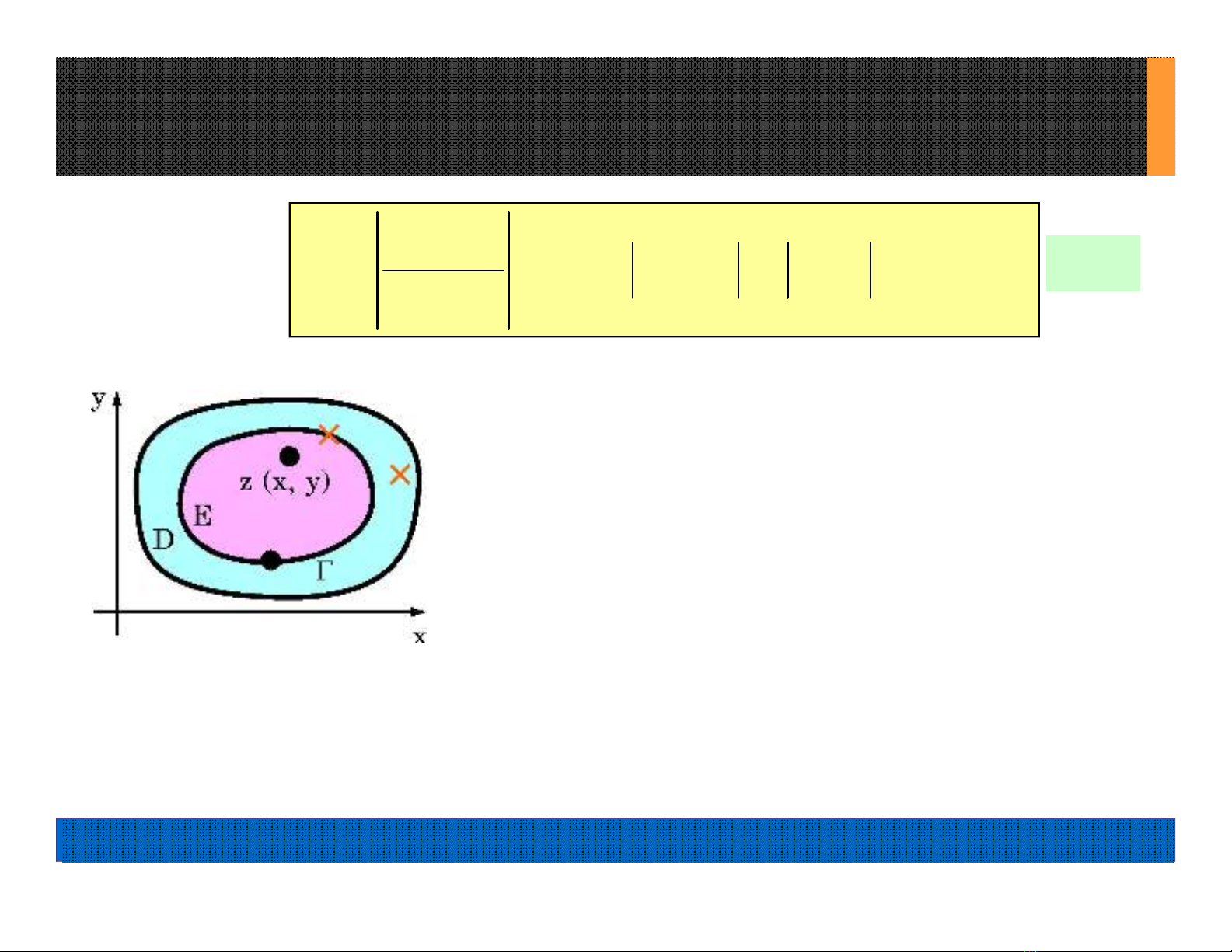
2. Phép thử tỉ số:
(9.8)
Đặt:
n 1 n
n n
n
f (z)
lim lim k (z) k(z) r(x,y)
f (z)
 
°(9.1) HTTĐ tại z(x, y) thỏa r(x, y) < 1 .
°(9.1) PK tại z(x, y) thỏa r(x, y) > 1.
°(9.1) có thể HT hoặc PK tại z(x, y)
thỏa r(x, y) = 1.
H9.2