Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 283
Chương 11: Ứng dụng của thặng dư
11.1 Tính tích phân xác định hàm lượng giác.
11.2 Tính tích phân suy rộng hàm hữu tỷ.
11.3 Tìm biến đổi Fourier.
11.4 Tìm biến đổi Laplace ngược.
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 284
11.1 Tính tích phân xác định hàm lượng giác:
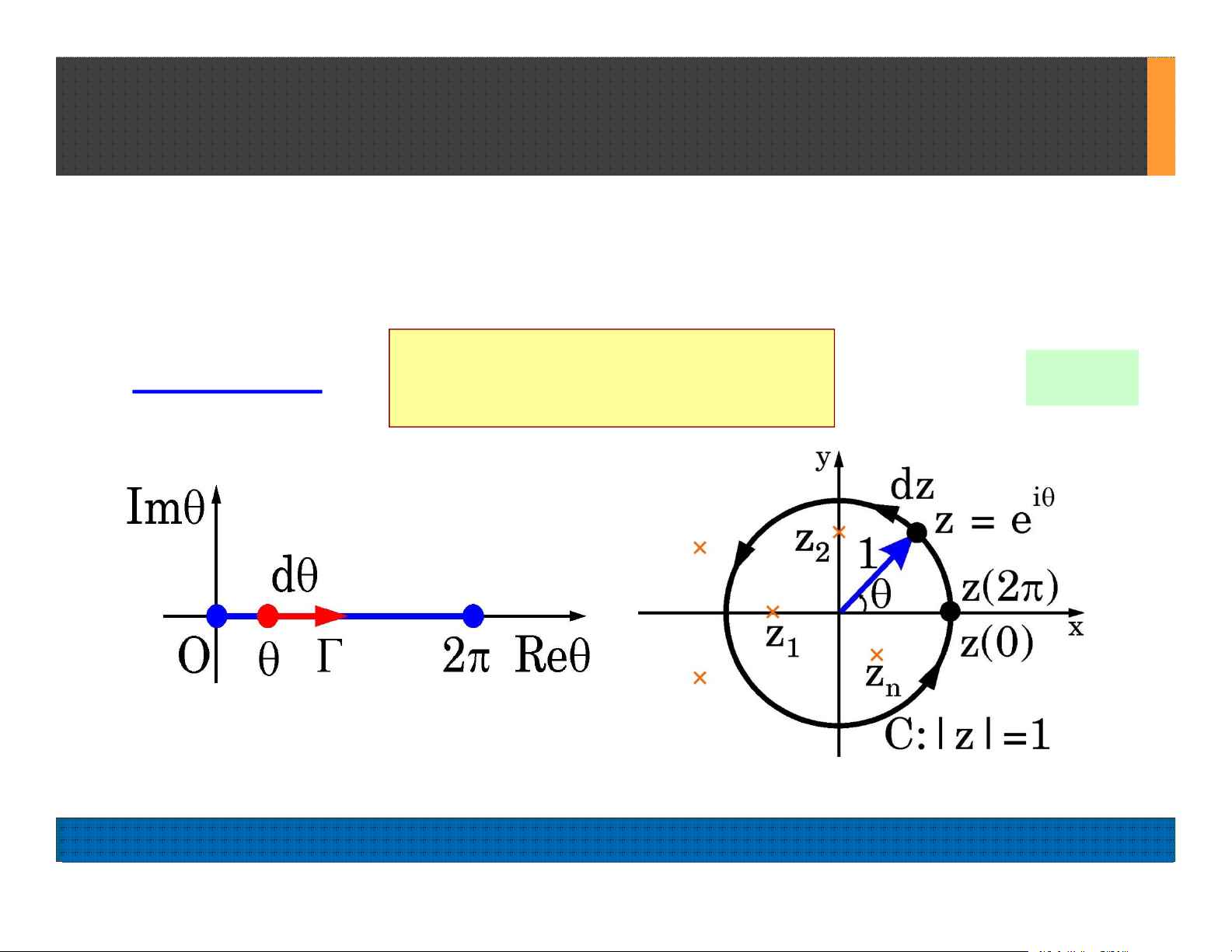
Gọi F(cos, sin) là 1 Hàm hữu tỷ của (cos, sin) hữu hạn trên
khoảng kín = [0, 2] (H11.1a)
1. Định nghĩa: (11.1)
2
0
I F(cos ,sin )d
H11.1(a) H11.1(b)
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 285
2. Cách tính tích phân xác định hàm lượng giác:
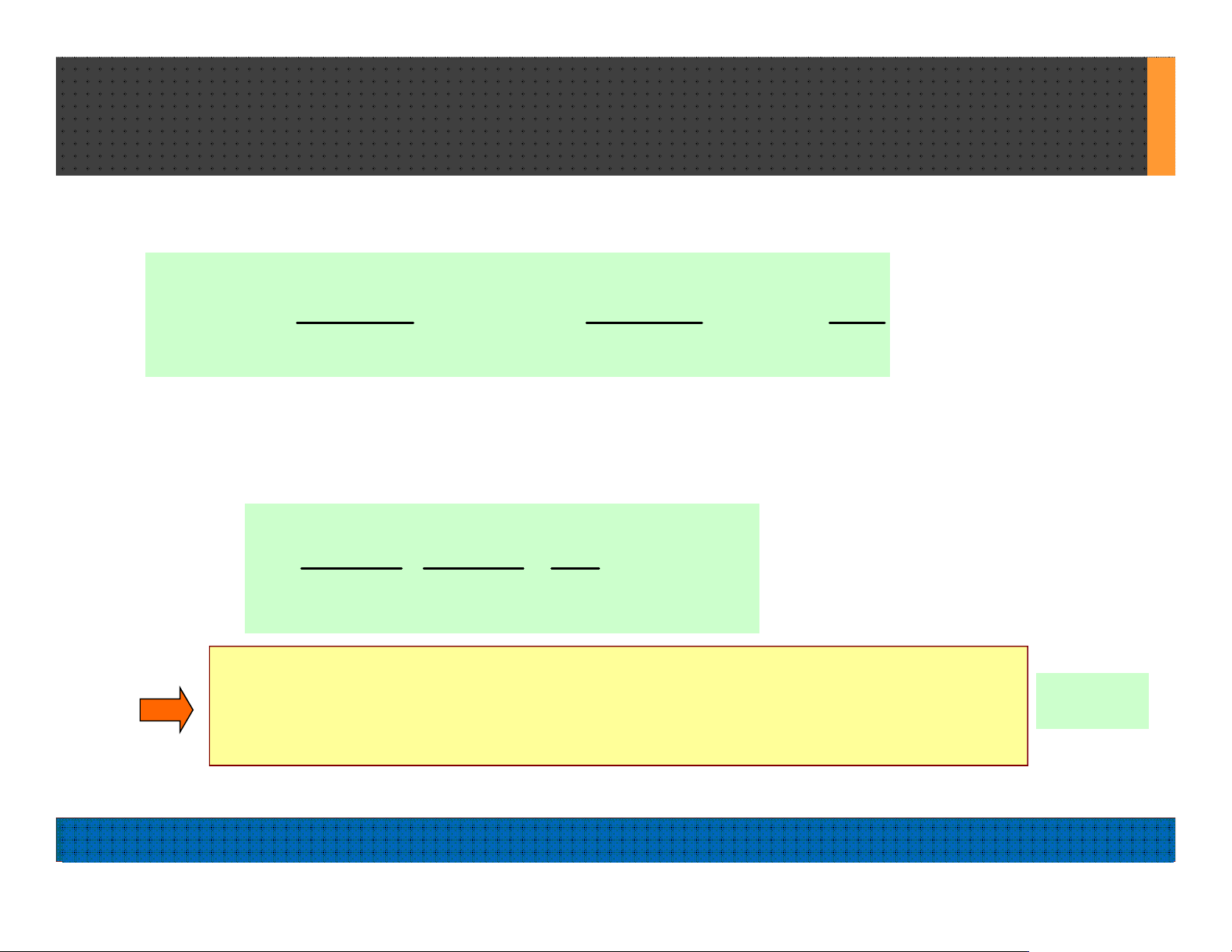
Đổi biến , ta có:
i
z e
2 2
cos ;sin ;d
2z 2iz iz
Đồng thời, đường tích phân biến thành Vòng Đơn Vị C : |z|
= 1 (H11.1b)
Đặt:
2 2
z 1 z 1 dz
F ; f(z)dz
2z 2iz iz
(11.2)
n
k k
C
k 1
I f(z)dz 2 i Res f(z); z (|z | 1)
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 286
3. Các bước để tính I :
B1. Tính f(z) từ phần 2.; f(z) là Hàm Hữu Tỷ P(z)/Q(z).
B2. Chọn các cực zk của f(z) có biên độ |zk| < 1 .
B3. Tính Thặng Dư tại mỗi cực đó.
B4. Tính tổng Thặng Dư rồi nhân cho 2i .
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 287
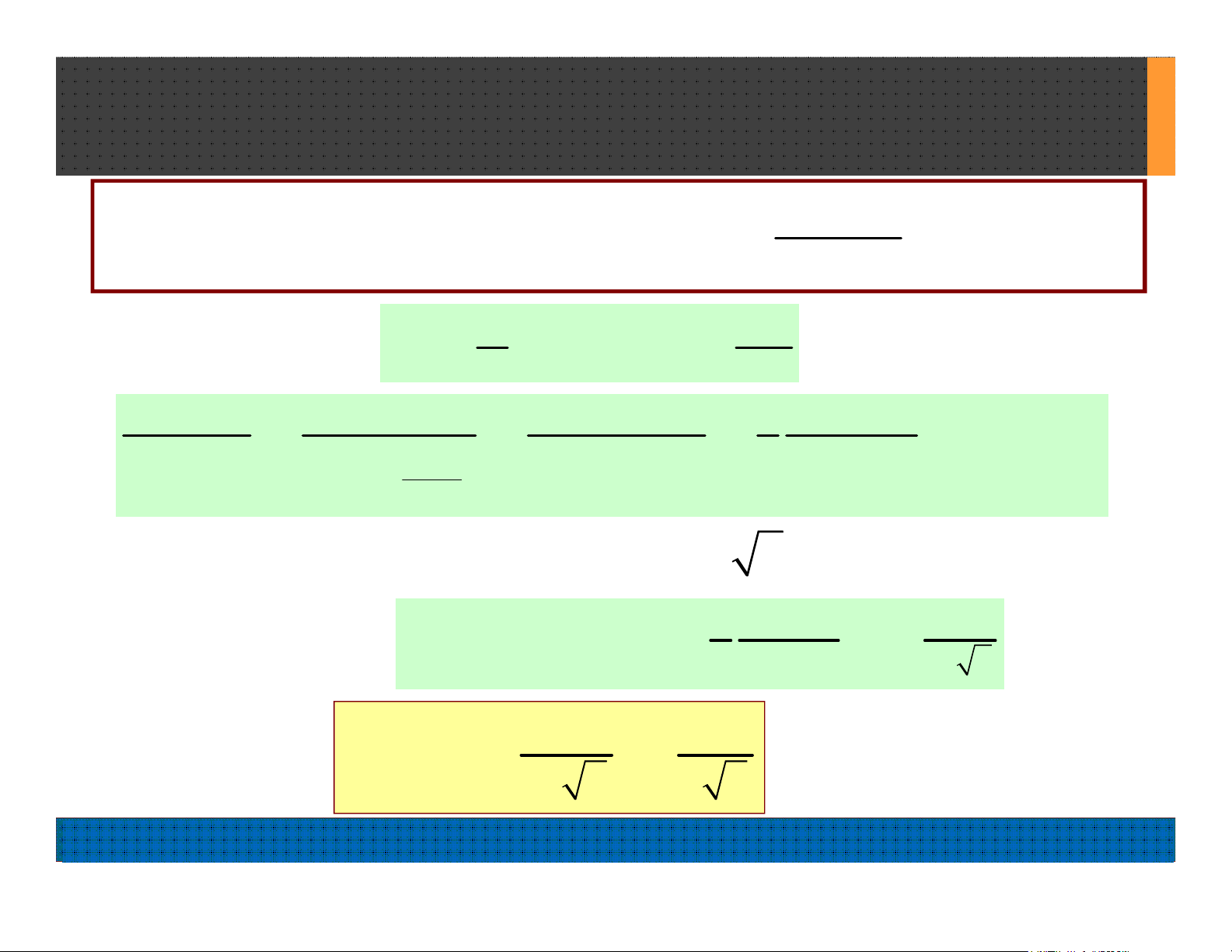
VD 11.1.1: Tính tích phân hàm lượng giác
2d
24 8cos
0
I
Dùng thặng dư, tính tích phân:
2
dz z 1
iz 2z
d & cos
Xác định f(z):
2 2 2
d dz dz i dz
24 8cos 4
z 1 i[24z 4z 4] [z 6z 1]
iz[24 4 ]
z
f(z)dz
1
z 3 2 2
Cực f(z) bên trong VTĐV:
Tính thặng dư:
1
i 1 i
14 [2z 6]
16 2
Res{f(z);z }
i
16 2 8 2
I 2 i
Cuối cùng: