BỘ CÔNG THƯƠNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰCBỘ CÔNG THƯƠNG - TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
BÀI TẬPBÀI TẬP
LÝ THUYẾT XÁC SUẤTLÝ THUYẾT XÁC SUẤT
VÀ THỐNG KÊ TOÁNVÀ THỐNG KÊ TOÁN
NĂM HỌC 2023 - 2024NĂM HỌC 2023 - 2024
BÀI TẬP TỔNG HỢP CHƯƠNG 1
(BIẾN CỐ NGẪU NHIÊN VÀ XÁC SUẤT)
?Công thức xác suất cổ điển
Câu hỏi 1
Một công ty cần tuyển 4nhân viên. Có 8người, gồm 3nam và 5nữ nộp đơn xin dự tuyển, và mỗi
người đều có cơ hội được tuyển như nhau. Tính xác suất để trong 4người được tuyển có ít nhất một
nữ?
Câu hỏi 2
Trước cổng trường đại học có 3quán cơm chất lượng ngang nhau. Có 3sinh viên, mỗi người độc lập
chọn một quán để ăn. Tính xác suất để:
a. 3sinh viên vào cùng một quán;
b. 2sinh viên vào cùng một quán, còn người kia thì vào quán khác.
Câu hỏi 3
Một hộp có 25 bóng đèn, trong đó có 3bóng hỏng. Một người lấy ngẫu nhiên 3bóng trong hộp để
kiểm tra. Tính xác suất để
a. có bóng hỏng;
b. số bóng hỏng nhiều hơn số bóng không hỏng.
?Công thức cộng và nhân xác suất
Câu hỏi 4
Ban giám đốc một công ty liên doanh với nước ngoài đang xem xét khả năng đình công của công
nhân để đòi tăng lương ở hai nhà máy Avà B. Kinh nghiệm cho họ biết rằng cuộc đình công ở nhà
máy Avà Bxảy ra lần lượt với xác suất là 0,65 và 0,55. Ngoài ra, họ cũng biết rằng nếu công nhân
ở nhà máy Bđình công thì có 80% khả năng để công nhân ở nhà máy Ađình công ủng hộ.
a. Tính xác suất để công nhân ở cả hai nhà máy đình công?
b. Nếu công nhân ở nhà máy Ađình công thì xác suất để công nhân ở nhà máy Bđình công để
ủng hộ bằng bao nhiêu?
Câu hỏi 5
Hai công ty Avà Bcùng kinh doanh một mặt hàng. Xác suất để công ty Athua lỗ là 0,3; xác suất
để công ty Bthua lỗ là 0,5. Tuy nhiên trên thực tế, khả năng cả hai công ty cùng thua lỗ là 0,2. Tìm
xác suất để
a. Chỉ có một công ty thua lỗ;
b. Có ít nhất một công ty làm ăn không thua lỗ.
2
Câu hỏi 6
Một máy có ba bộ phận hoạt động độc lập với nhau. Xác suất để các bộ phận bị hỏng lần lượt là
0,2; 0,3và 0,1. Tính xác suất của các biến cố sau:
a. Có đúng 2bộ phận bị hỏng;
b. Có ít nhất 1bộ phận bị hỏng.
Câu hỏi 7
Một nhân viên bán hàng mỗi năm đến chào hàng ở công ty Aba lần. Xác suất để lần đầu bán được
hàng là 0,7. Nếu lần trước bán được hàng thì xác suất để lần sau bán được hàng là 0,8, còn nếu lần
trước không bán được hàng thì xác suất để lần sau bán được hàng chỉ là 0,5. Tìm xác suất để:
a. Cả ba lần đều bán được hàng;
b. Có đúng hai lần bán được hàng.
Câu hỏi 8
Một mạng điện gồm ba bóng đèn mắc song song. Xác suất bị cháy của các bóng đèn 1,2,3tương ứng
là 0,15; 0,3và 0,2. Tìm xác suất để
a. Mạng điện bị mất điện(cả 3bóng đèn đều bị cháy);
b. Có một bóng đèn bị cháy.
Câu hỏi 9
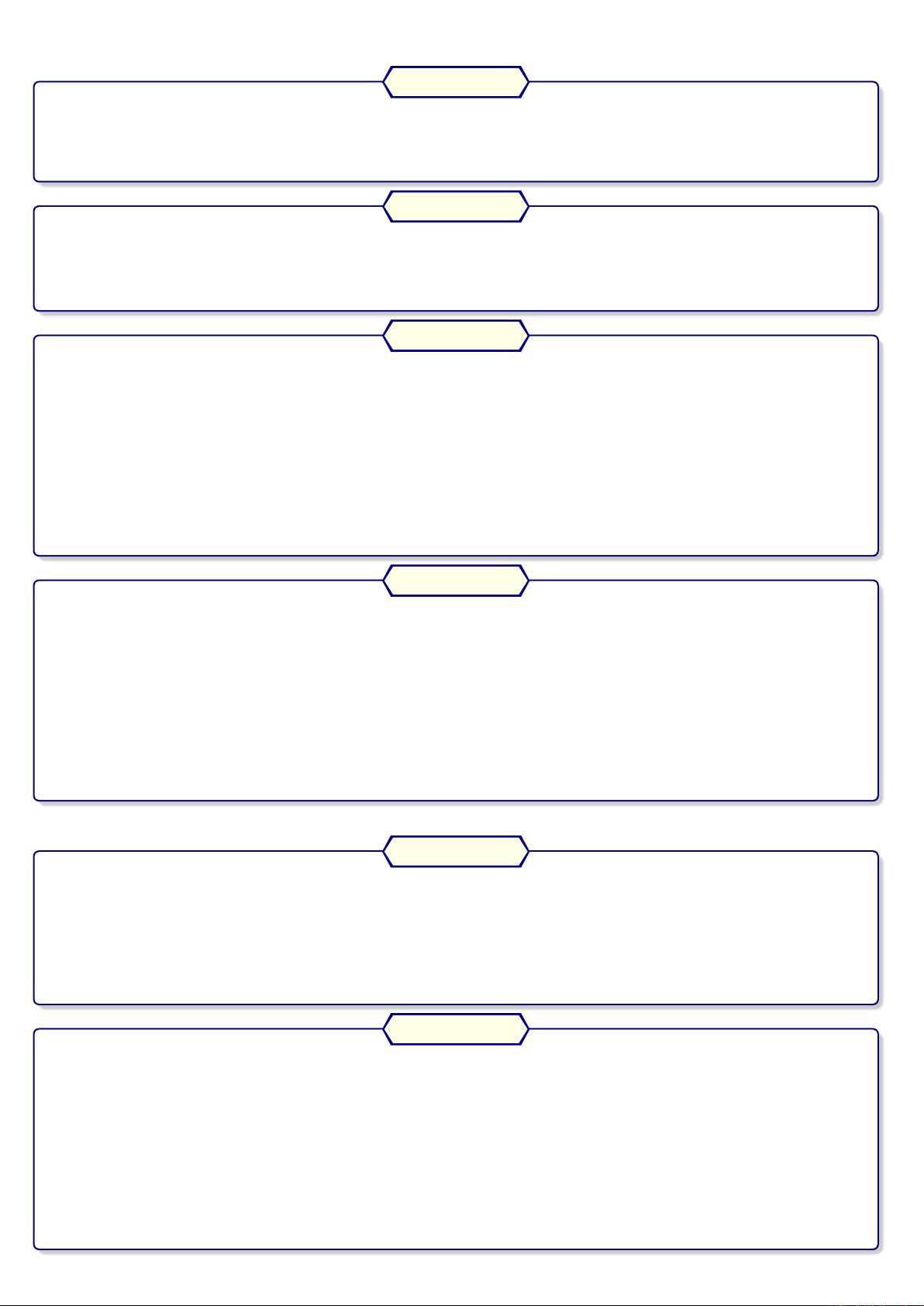
Một mạng cung cấp điện như hình vẽ
Điện được cung cấp từ Etới khu tiêu dùng Fqua năm trạm biến áp A, B, C, D, G. Các trạm biến
áp này hoạt động độc lập với nhau. Xác suất để mỗi trạm biến áp A, B, C có sự cố kỹ thuật sau thời
gian hoạt động là 0,15, xác suất với 2trạm D, G là 0,2. Tìm xác suất để khu vực Fkhông bị mất
điện.
Câu hỏi 10
Có 5linh kiện điện tử, xác suất để mỗi linh kiện hỏng tại một thời điểm bất kỳ lần lượt là
0,02; 0,03; 0,04; 0,05; 0,06. Các linh kiện điện tử hoạt động độc lập với nhau. Giả sử 5linh kiện
đó được lắp vào mạch điện theo sơ đồ dưới đây. Tính xác suất để trong mạch có dòng điện chạy qua
tại một thời điểm bất kỳ.
3
Câu hỏi 11
Có 5bóng đèn được mắc song song vào một mạch điện. Xác suất để mỗi bóng đèn bị hỏng tại một
thời điểm bất kỳ lần lượt là 0,02; 0,03; 0,05; 0,06; 0,08. Hãy tính xác suất để trong mạch có dòng
điện chạy qua tại một thời điểm bất kỳ.
Câu hỏi 12
Một mạch điện gồm hai bộ phận mắc nối tiếp, với khả năng làm việc tốt trong một khoảng thời gian
nào đó của mỗi bộ phận là 0,93 và 0,95. Ở một thời điểm trong khoảng thời gian trên người ta thấy
mạch điện ngừng làm việc(do bộ phận nào đó bị hỏng). Tính xác suất để bộ phận thứ 2bị hỏng?
Câu hỏi 13
Trong một cửa hàng, người ta mắc hai hệ thống bóng đèn độc lập. Hệ thống I gồm 4bóng đèn mắc
nối tiếp, hệ thống II gồm 3bóng đèn mắc song song. Khả năng bị hỏng của mỗi bóng đèn trong 24
giờ thắp sáng liên tục là 0,2. Việc hỏng của mỗi bóng đèn trong hệ thống được xem như độc lập và
hệ thống được coi là bị hỏng nếu tất cả các bóng đèn trong hệ thống đều không sáng. Tính xác suất
để:
a. Cả hai hệ thống bị hỏng;
b. Chỉ có một hệ thống bị hỏng.
Câu hỏi 14
Trên một bảng quảng cáo, người ta mắc hai hệ thống bóng đèn độc lập. Hệ thống I gồm 4bóng đèn
mắc nối tiếp, hệ thống II gồm 3bóng đèn mắc song song. Khả năng bị hỏng của mỗi bóng đèn trong
18 giờ thắp sáng liên tục là 0,25. Việc hỏng của mỗi bóng đèn trong hệ thống được xem như độc lập
và hệ thống được coi là bị hỏng nếu tất cả các bóng đèn trong hệ thống đều không sáng. Tính xác
suất để:
a. Hệ thống I bị hỏng;
b. Hệ thống II không bị hỏng.
?Công thức xác suất đầy đủ và Bayes
Câu hỏi 15
Một lô hàng có 60% sản phẩm của máy Avà 40% sản phẩm của máy B. Tỷ lệ phế phẩm của các máy
tương ứng là 5% và 3%. Lấy ngẫu nhiên 1sản phẩm để kiểm tra:
a. Tìm xác suất để lấy được phế phẩm;
b. Giả sử đã lấy được phế phẩm thì phế phẩm đó có khả năng do máy nào sản xuất là nhiều hơn.
Câu hỏi 16
Một nhà máy có 3phân xưởng. Phân xưởng I có tỷ lệ phế phẩm là 4%; phân xưởng II có tỷ lệ phế
phẩm là 6% và phân xưởng III có tỷ lệ phế phẩm 9%. Biết rằng năng suất chế tạo sản phẩm của
phân xưởng I, II là như nhau và năng suất của phân xưởng III bằng năng suất của phân xưởng I và
II cộng lại.
a. Từ kho của nhà máy, lấy ra ngẫu nhiên 1 sản phẩm để kiểm tra. Tìm xác suất để lấy được phế
phẩm?
b. Giả sử đã lấy được chính phẩm. Tìm xác suất để sản phẩm đó do phân xưởng II sản xuất?
4
Câu hỏi 17
Một hộp đựng 10 phong bì bốc thăm trúng thưởng, trong đó có 4phong bì đựng 500 nghìn và 6phong
bì đựng 100 nghìn. Bốc ngẫu nhiên liên tiếp hai phong bì. Nếu biết phong bì thứ hai có 500 nghìn,
tìm xác suất để phong bì đầu tiên cũng có 500 nghìn?
Câu hỏi 18
Có hai lô sản phẩm: Lô I có 7chính phẩm và 3phế phẩm, lô II có 6chính phẩm và 4phế phẩm. Lấy
ngẫu nhiên 1sản phẩm từ lô I bỏ sang lô II rồi từ lô II lấy ngẫu nhiên một sản phẩm. Tính xác suất
để sản phẩm lấy ra sau cùng là chính phẩm?
Câu hỏi 19
Hai máy tiện cùng sản xuất ra một loại trục xe đạp như nhau. Các trục xe được đóng chung vào một
kiện. Năng suất của máy tiện thứ hai gấp đôi năng suất của máy tiện thứ nhất. Máy tiện thứ nhất
sản xuất trung bình được 85% trục loại tốt, máy tiện thứ hai sản xuất trung bình được 83% trục loại
tốt. Lấy ngẫu nhiên từ kiện một trục, tìm xác suất để lấy được trục loại tốt?
Câu hỏi 20
Có hai lô hàng: lô thứ nhất có 7chính phẩm và 3phế phẩm, lô thứ hai có 6chính phẩm và 4phế
phẩm. Chọn ngẫu nhiên 1lô và từ đó lấy ngẫu nhiên ra 2sản phẩm:
a. Tìm xác suất để lấy được 2chính phẩm?
b. Giả sử đã lấy được 2chính phẩm. Tìm xác suất để đó là 2sản phẩm của lô thứ nhất?
5