Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 152
Chương 6: Ứng dụng biến đổi Laplace vào giải tích
mạch điện.
6.1 Đại cương.
6.2 Họ hàm bất thường.
6.3 Biến đổi Laplace của họ hàm bất thường.
6.4 Quan hệ áp – dòng miền t.
6.5 Định luật Kirchhoff miền t.
6.6 Quan hệ áp – dòng miền s.
6.7 Định luật Kirchhoff miền s.
6.8 Tổng trở và tổng dẫn miền s.
6.9 Các bước giải mạch dùng biến đổi Laplace.
6.10 Hàm truyền.
6.11 Giải mạch dùng hàm truyền khi điều kiện đầu khác 0.
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 153
6.1 Đại cương:
Giải mạch miền t: Hệ phương trình vi phân.
Giải mạch miền s: Hệ phương trình đại số.
Nguồn sin: Tổng trở phức , chỉ dùng tính đáp ứng cưỡng bức.
Nguồn bất kỳ, kể cả nguồn bất thường : Tổng trở miền s, Z(s).
Phương pháp này tìm được đáp ứng tổng gồm có đáp ứng tự
nhiên và đáp ứng cưỡng bức.
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 154
6.2 Họ hàm bất thường:
1. Họ hàm bước:
Hàm bước đơn vị:
0 0
1 0
t
u(t ) t
(6.1)
Hàm bước đơn vị trễ t0giây:
0
0
0
0
1
t t
u(t t )
t t
(6.2)
Hàm lọc hay hàm cổng:
0 1
u(t t ) u(t t )
(6.3)
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 155
2. Họ tích phân hàm bước:
Hàm dốc đơn vị:(6.4)
0
r(t) u( ) tu(t)
td
tt
p(t ) r ( )d u(t )
!
2
0
(6.5)
3
0
t
c(t) p( ) u(t)
3!
td
(6.6)
n
n n-1
0
t
p (t) p ( ) u(t)
n!
td
(6.7)
Hàm parabôn đơn vị:
Hàm bậc ba đơn vị:
Hàm bậc n đơn vị:
Bài giảng Toán kỹ thuật –Khoa Điện & Điện tử –ĐHBKTPHCM 156
3. Họ đạo hàm hàm bước:
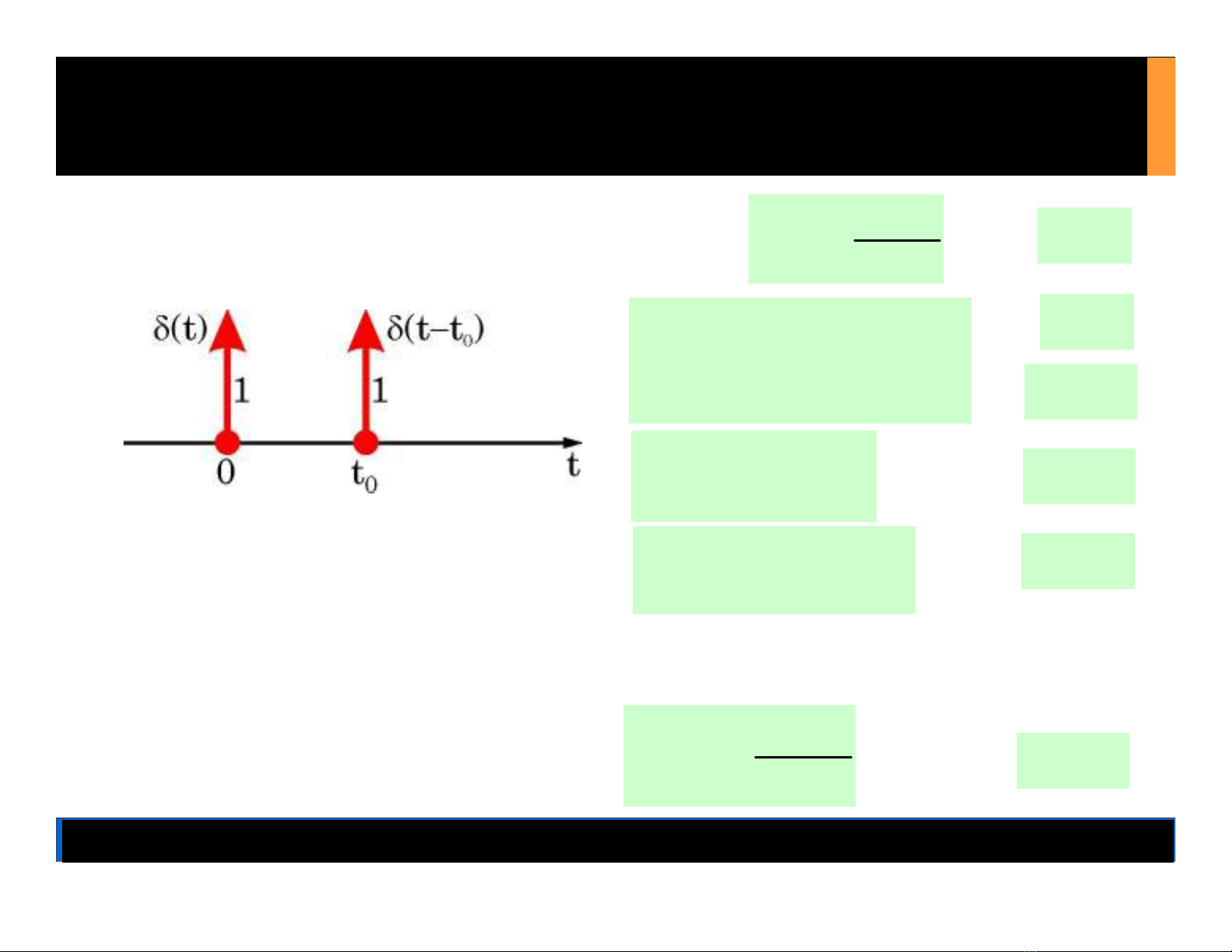
Hàm xung đơn vị (xung Dirac):
Hàm xung đơn vị chậm t0giây: (t –t0).
Hàm xung đôi đơn vị:
(6.8)
du(t )
(t )
dt
H6.1
(6.9)
0 0
0
(t )
(t )
(t )
(6.10)
1
(t )dt
(6.11)
t
u(t ) ( )d
(6.12)
'
d (t )
(t )
dt
(6.13)