Trường Đại học Công nghiệp thành phố Hồ Chí Minh
Khoa Công nghệ Cơ khí
CHƯƠNG 04:
TỐI ƯU HÀM NHIỀU BIẾN SỐ
VỚI RÀNG BUỘC ĐẲNG THỨC:
PHƯƠNG PHÁP CỔ ĐIỂN
Thời lượng: 3 tiết
2
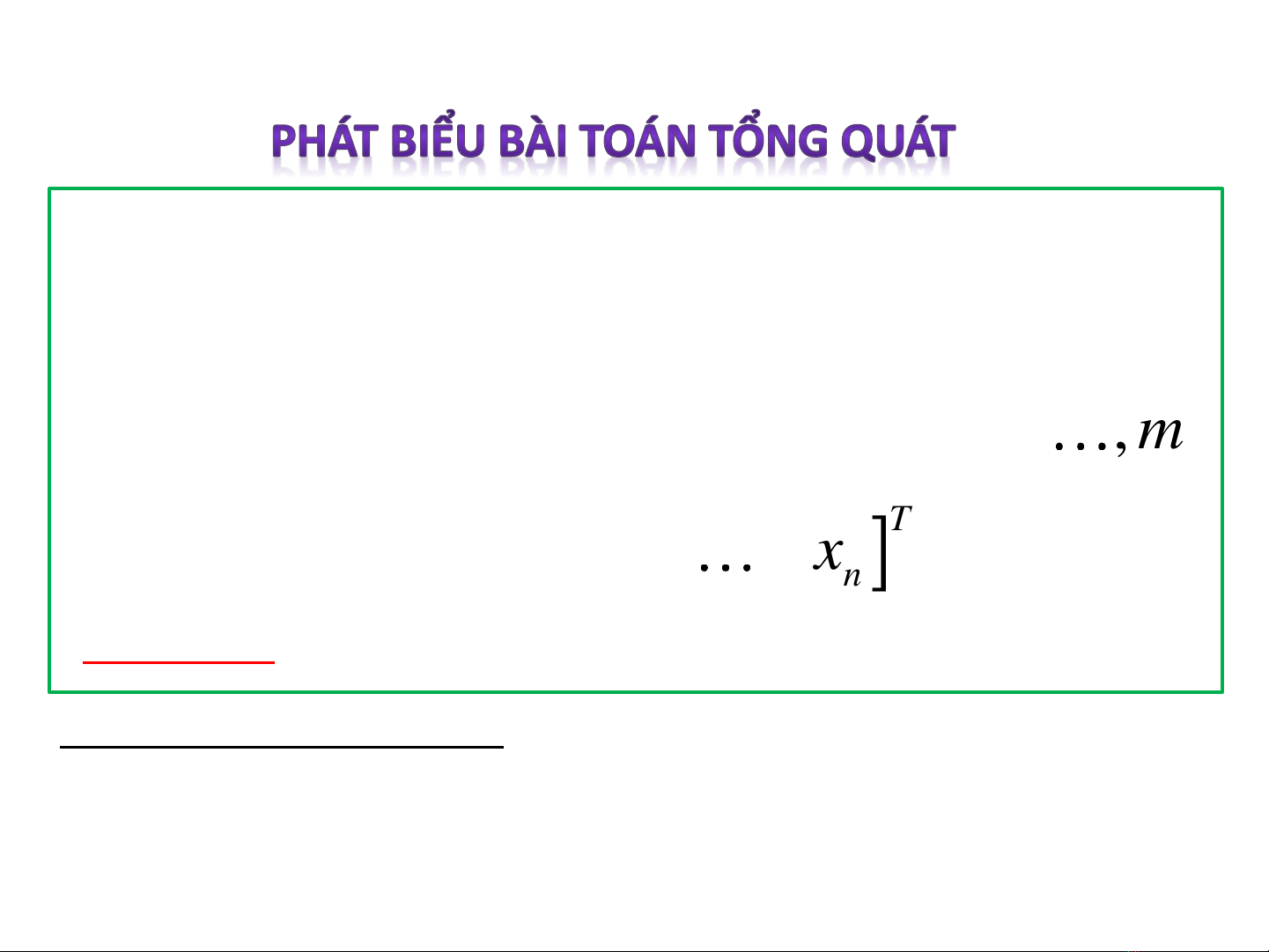
Tối ưu hàm nhiều biến với ràng buộc đẳng thức
Tìm cực tiểu (Minimum) của hàm nhiều biến sau:
Với các điều kiện ràng buộc đẳng thức:
0
1, 2, ,
j
g
jm
x
Với:
12
T
n
x x xx
Điều kiện: m ≤ n Nếu m > n bài toán sẽ không có lời giải.
Có 3 phương pháp giải:
1. Phương pháp thế trực tiếp (direct substitution)
2. Phương pháp biến đổi ràng buộc (constrained variation)
3. Phương pháp nhân tử Lagrange (Lagrange multipliers)
fx
3
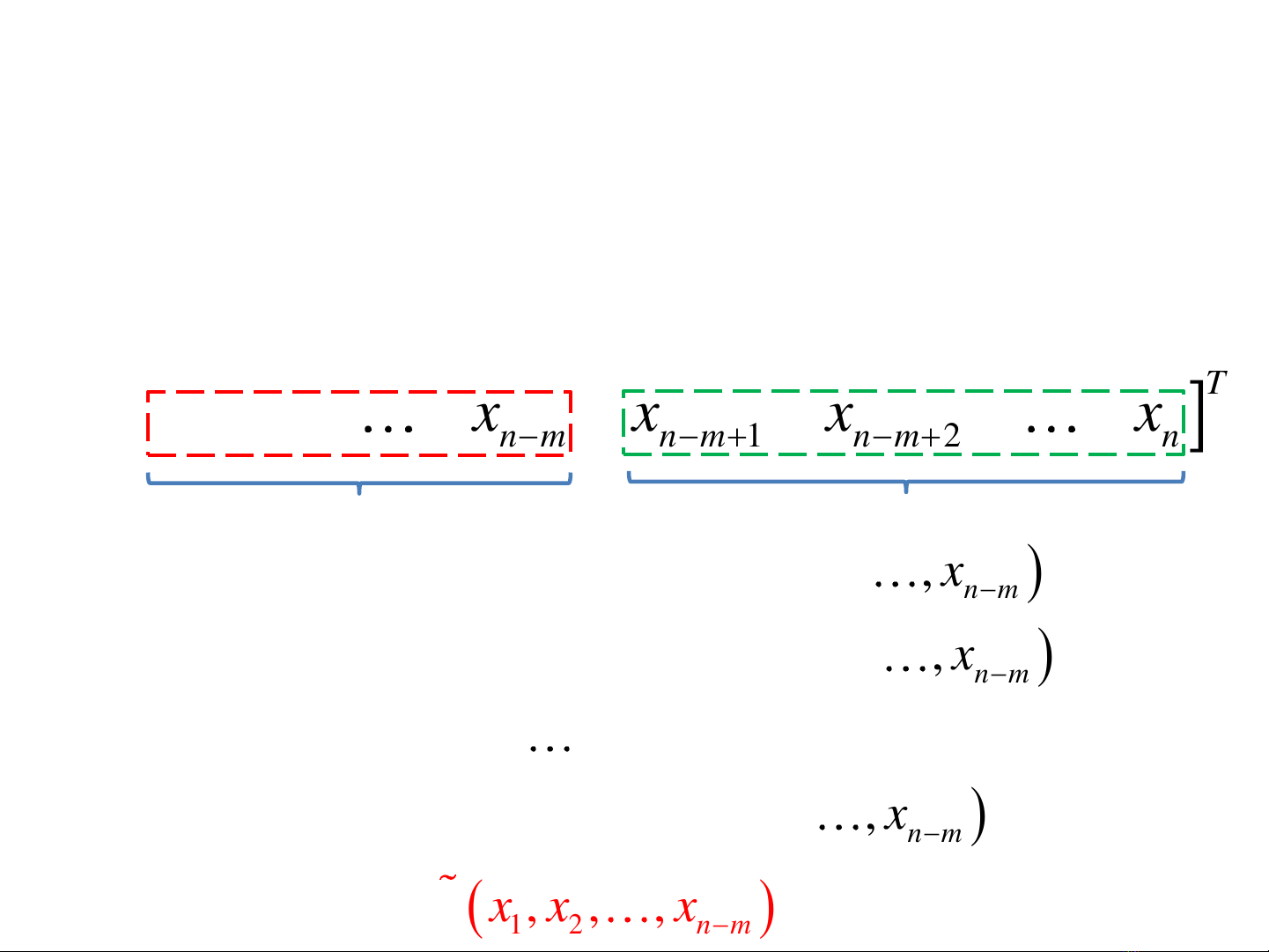
Phương pháp thế trực tiếp
Từ m ràng buộc đẳng thức, ta biến đổi và thu được các biểu thức
tính m biến số thông qua (n-m) biến số còn lại (trong số n biến số
tất cả). Từ đó thế vào biểu thức hàm f ban đầu. Như vậy hàm f sẽ
trở thành hàm có (n-m) biến số nhưng không còn ràng buộc nào
hết. Ta quay trở về bài toán tối ưu không ràng buộc.
1 1 1 2
2 2 1 2
2
12
1
, , ,
0, , ,
1..
,,
, , , m
,
in
n m n m
j
n
n m n m
n m m
m
n
x h x x x
gx h x x x
jm
xh
xfx
xx
fx
x



x
x
1 2 1 2
T
n m n m n m n
x x x x x x
x
(n-m) tham biến cơ sở m tham biến cần triệt tiêu trong f
Từ:
Hàm (n-m) biến số
4
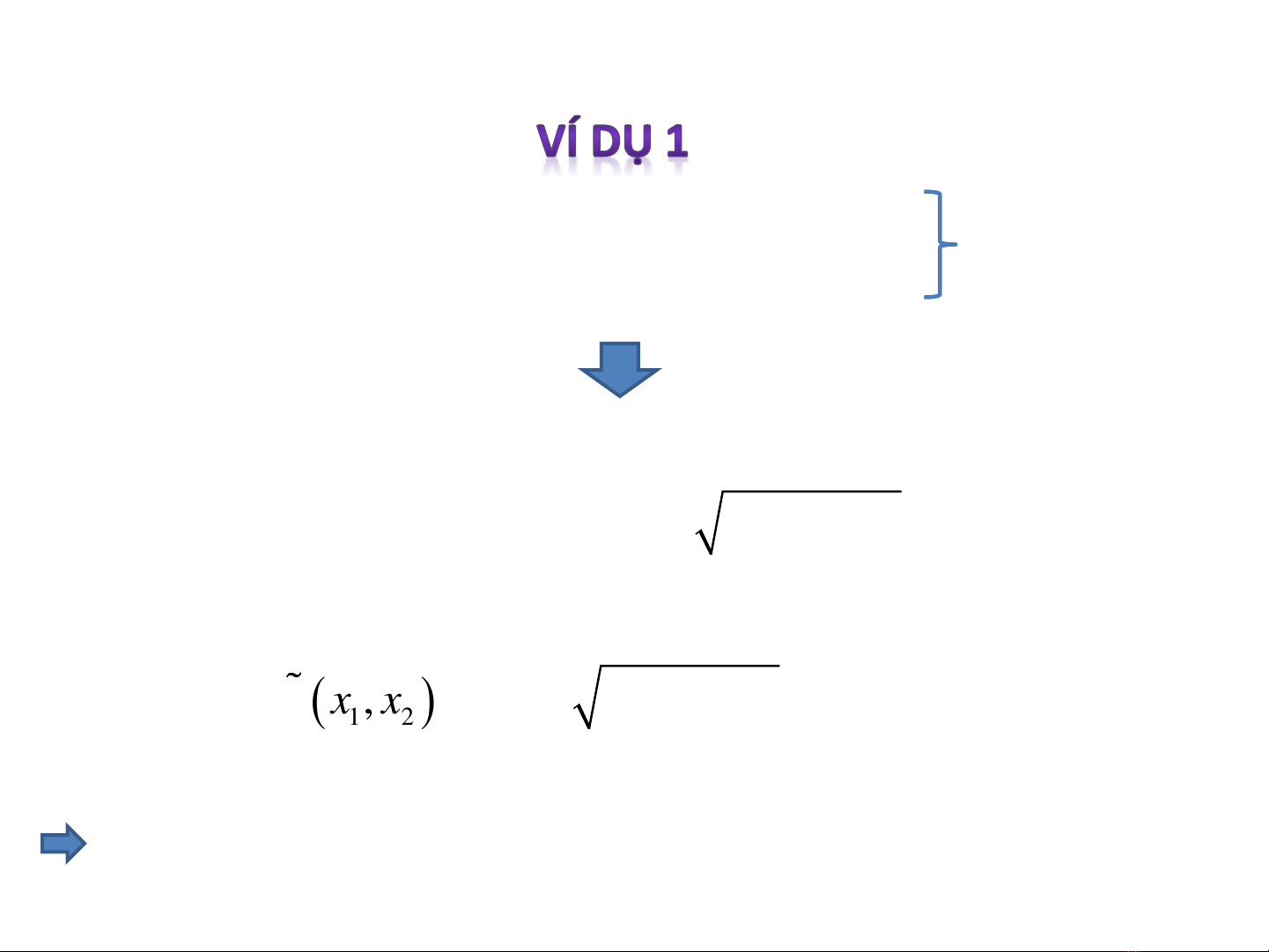
Phương pháp thế trực tiếp
Tối ưu hàm số sau:
1 2 3 1 2 3
, , 8f x x x x x x
Với ràng buộc:
222
1 2 3
1xxx
3
1
n
m
Tìm biểu thức liên hệ của 1 tham biến vào 2 tham biến còn lại:
Thế vào hàm f ban đầu:
22
1 2 3 1 2 1 2 1 2
, , , 8 1f x x x f x x x x x x
Tối ưu hàm 2 biến
không ràng buộc
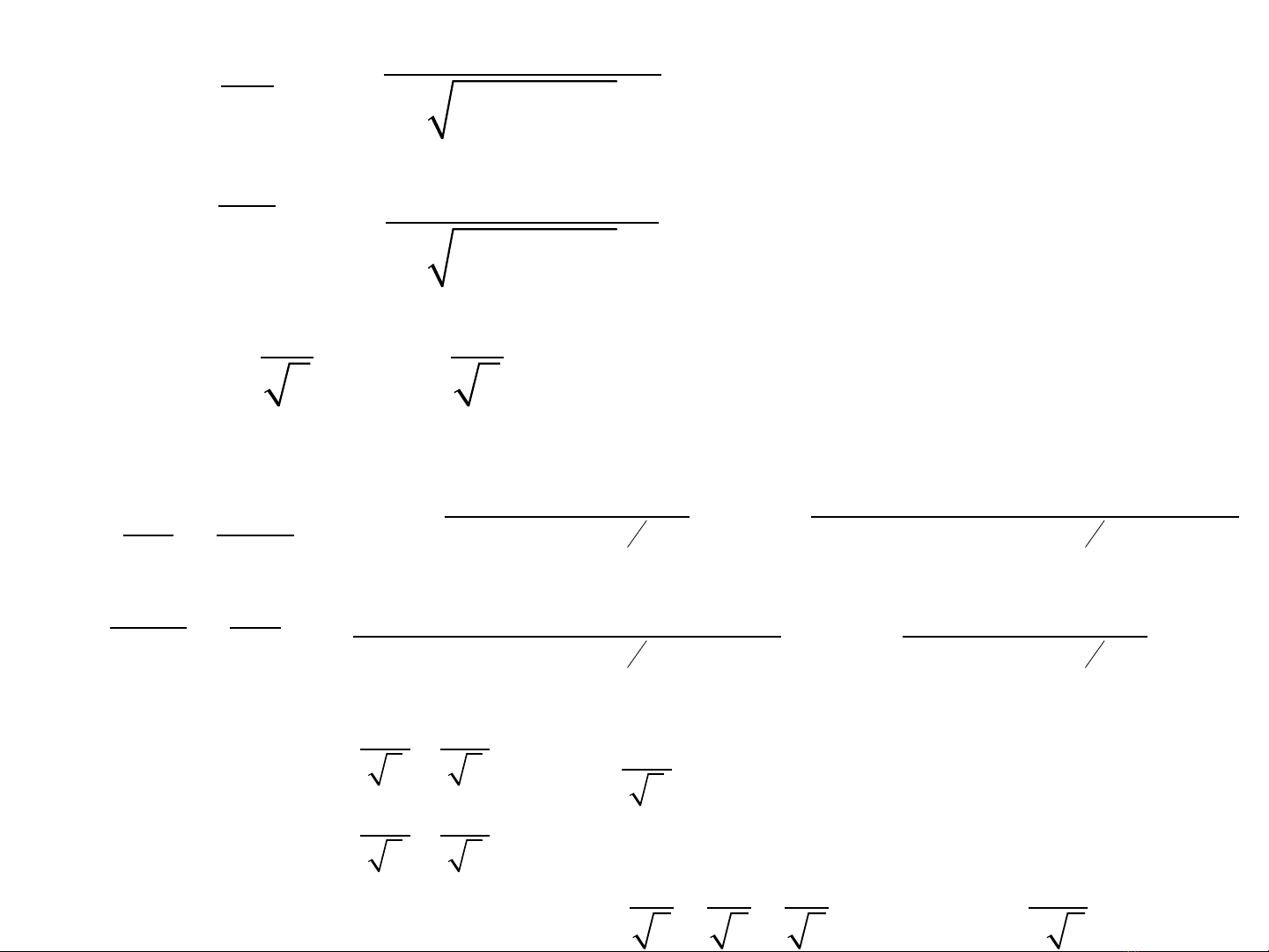
Giải hệ phương trình Gradient = 0:
5
22
2 1 2
22 22
12
1 1 2
22
22
12
1 1 2
22
2
12
1 2 3
8 2 1
12 1 0
0
2 1 0
8 2 1
1
11
33
x x x
f
xx
x x x
ffxx
x x x
xxx
x x x














 


x
Tính ma trận Hessian tại điểm dừng:
2 2 4 2 2 4 2 2
1 2 1 2 1 1 2 2 1 2
22
33
2 2 2 2
22
2
1 2 1 2
1 1 2
22 4 2 2 4 2 2 2 2
1 1 2 2 1 2 1 2 1 2
233
2 1 2 2 2 2 2
22
1 2 1 2
8 2 3 3 8 2 3 2 3 3 1
11
8 2 3 2 3 3 1 8 2 3 3
11
x x x x x x x x x x
ff
x x x x
x x x
ff x x x x x x x x x x
x x x x x x x

















H
1
2
32 16 32 0
33 3
16 32 256 0
33
A
A











Điểm dừng
Điểm cực đại
Vậy cực đại của hàm ban đầu là:
1 1 1 8 max
3 3 3 3 3
T
f



**
xx