1
Chương 5
ĐiỀU KHIỂN VECTOR
ĐỘNG CƠ KHÔNG ĐỒNG BỘ
2
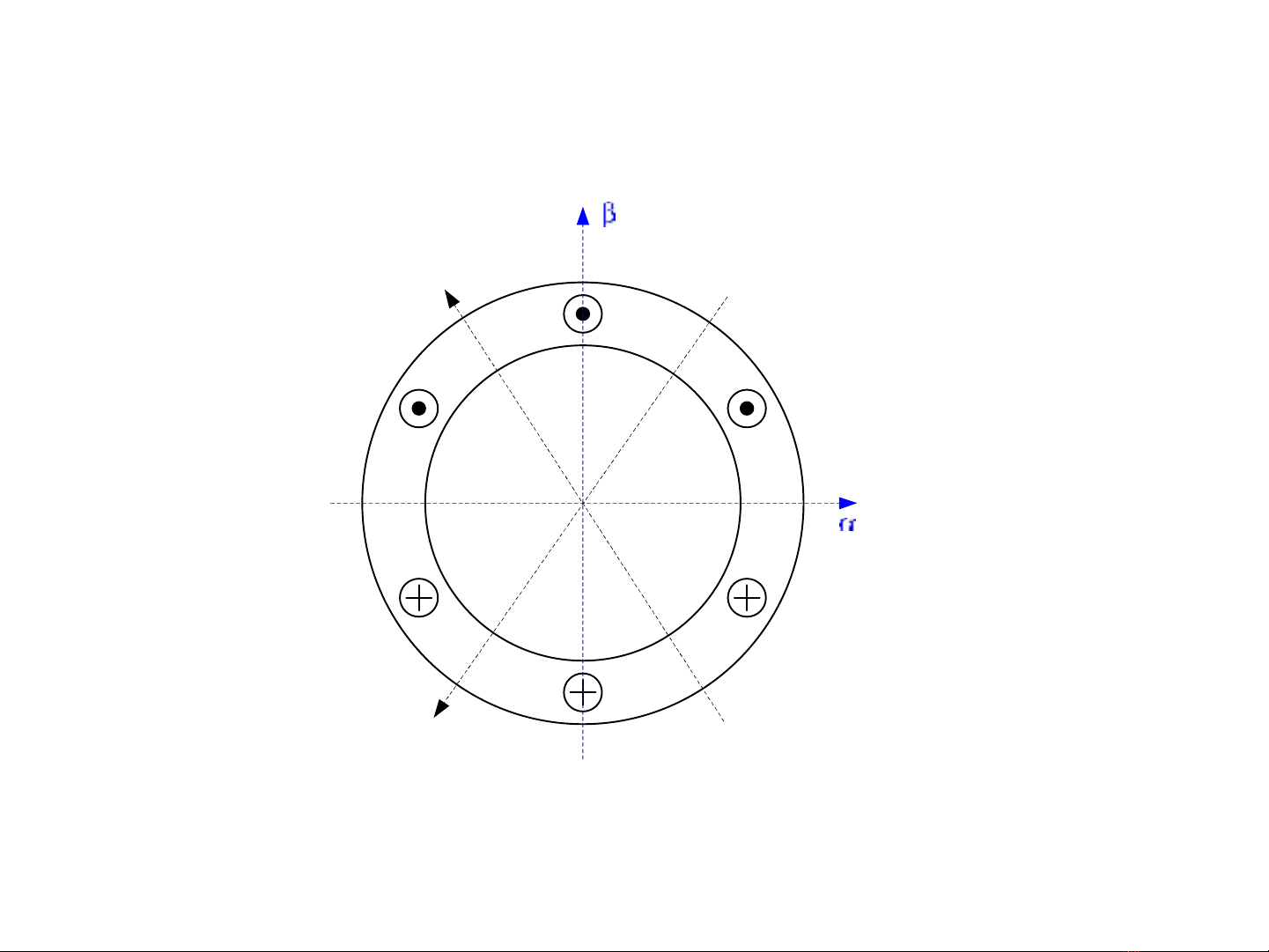
Vector không gian – Hệ tọa độ abc và

Trục pha A
Trục pha C
Trục pha B
A
A’
B
B’
C
C’
Hệ trục tọa độ abc và hệ trục tọa độ
3
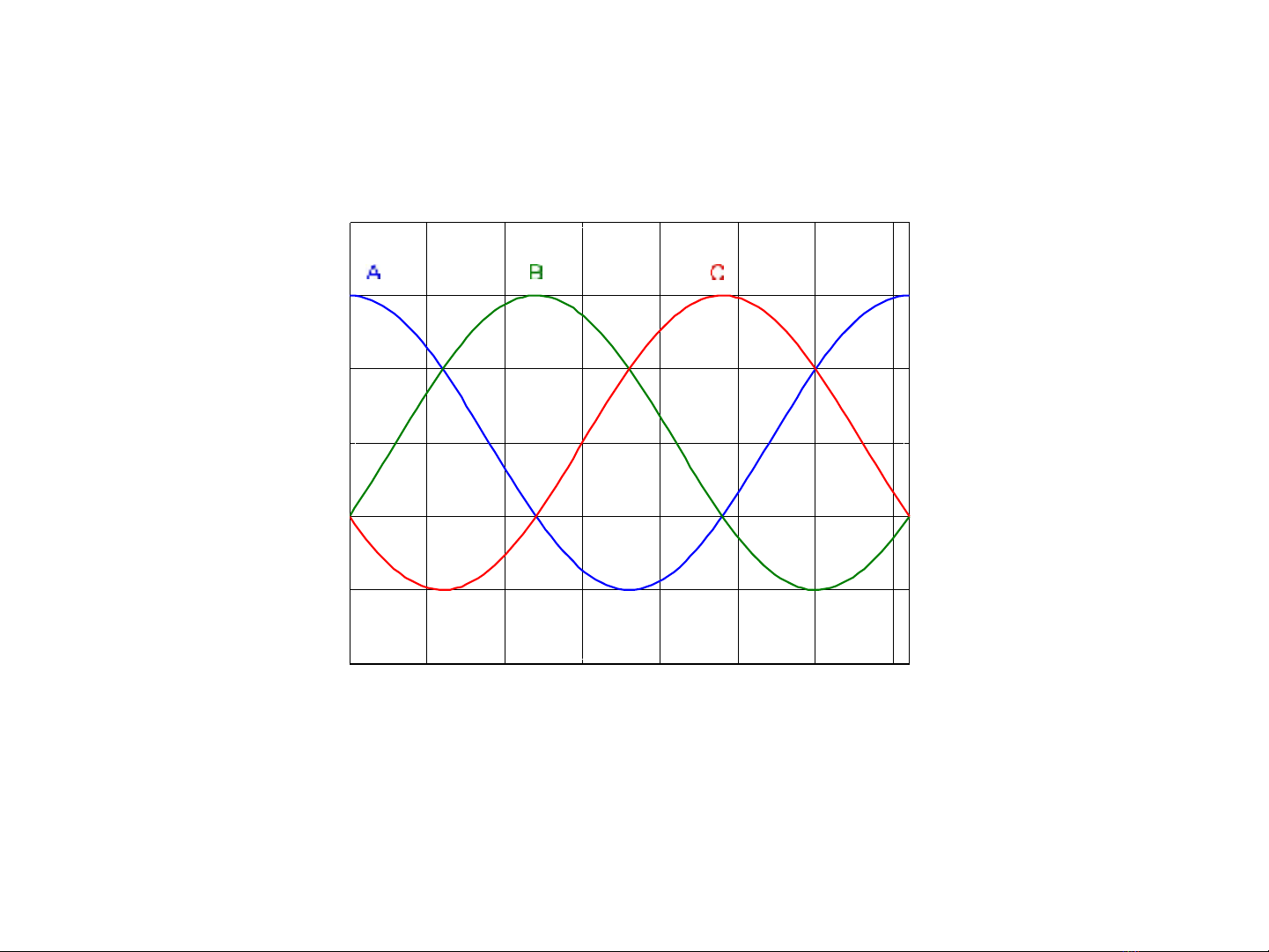
Vector không gian – Hệ tọa độ abc và

0 50 100 150 200 250 300 350
Sức từ động 3 pha
4
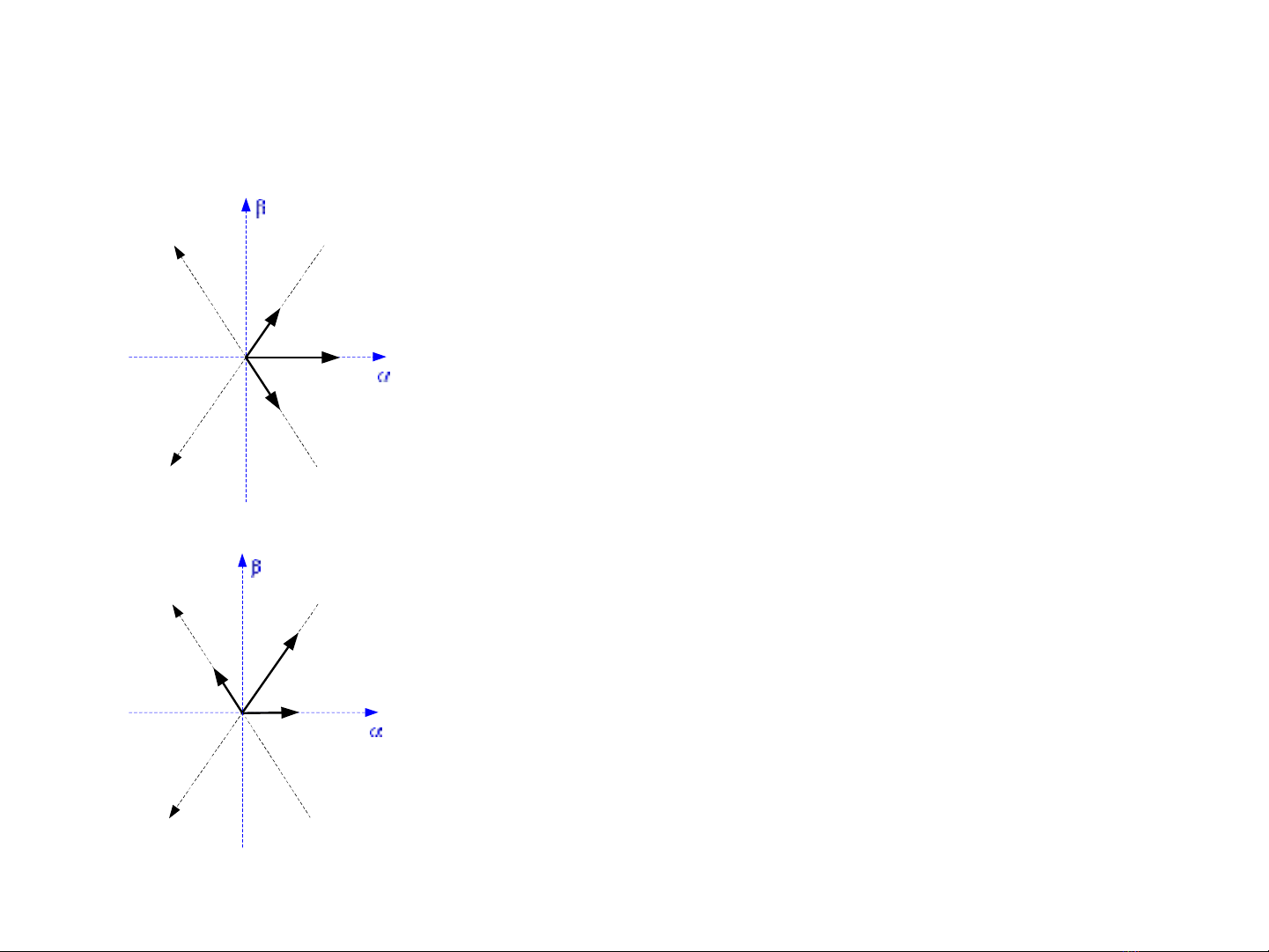
Vector không gian – Hệ tọa độ abc và

Trục pha A
Trục pha C
Trục pha B
Fas
Fbs
Fcs
Trục pha A
Trục pha C
Trục pha B
Fas
Fbs
Fcs
Các vector sức từ động trong trường hợp:
0
o
t
Các vector sức từ động trong trường hợp:
60
o
t
5
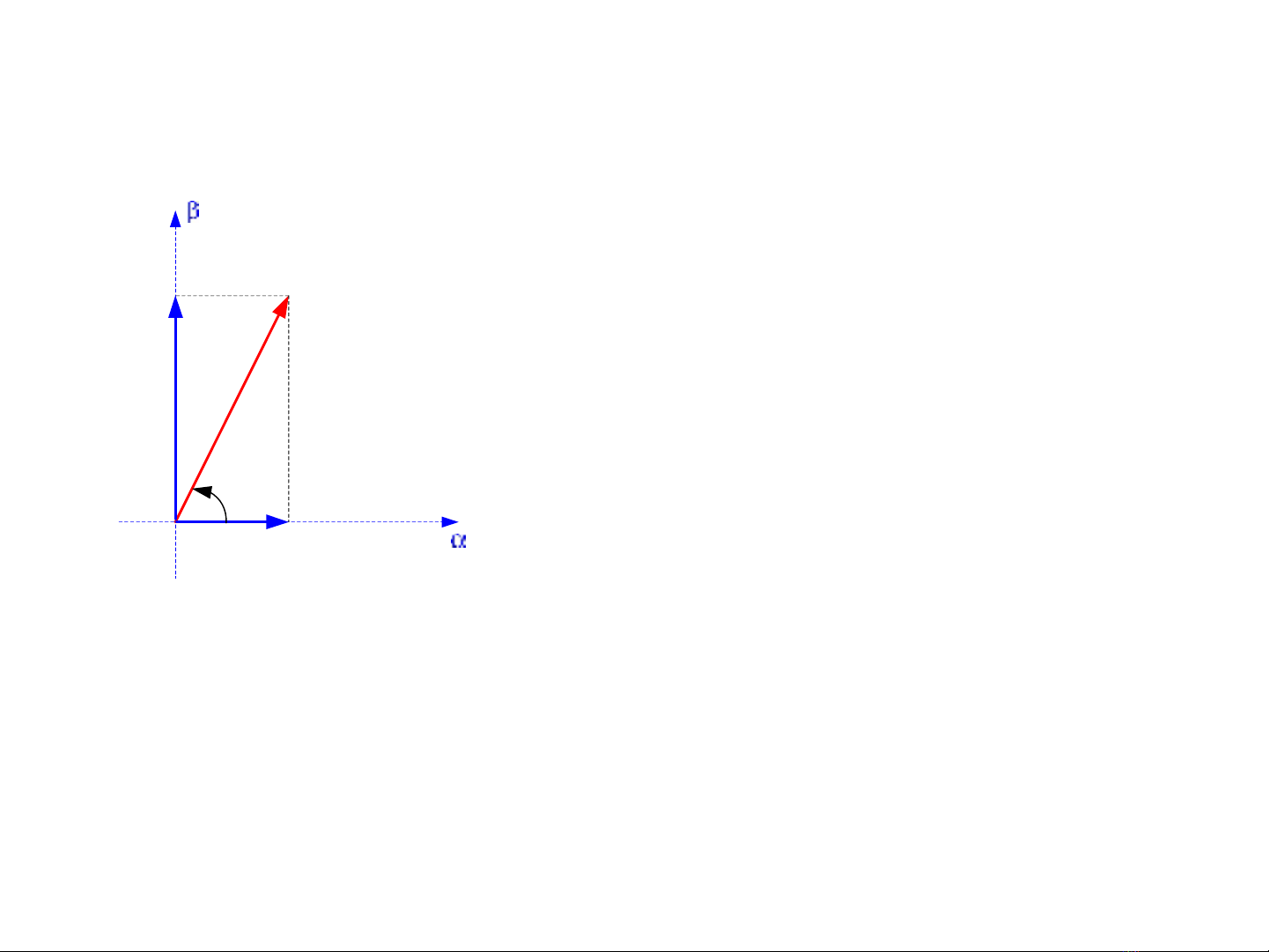
Vector không gian – Hệ tọa độ abc và

S
F
S
s
F
S
s
F
s
t
Vector sức từ động tổng
Vector sức từ động tổng
s
s
F
được định nghĩa là:
0 120 240
o o o
j j j
as bs cs
F e F e F e
s
s
F