1
BAØI GIAÛNG
XAÙC SUAÁT THOÁNG KEÂ
(GV: Traàn Ngoïc Hoäi - 2009)
CHÖÔNG 2
ÑAÏI LÖÔÏNG NGAÃU NHIEÂN
VAØ PHAÂN PHOÁI XAÙC SUAÁT
§1. Khaùi nieäm veà ñaïi löôïng ngaãu nhieân.
1.1. Ñònh nghóa. Ñaïi löôïng ngaãu nhieân hay bieán ngaãu nhieân laø moät
ñaïi löôïng nhaän giaù trò thöïc tuøy theo keát quaû cuûa pheùp thöû. Ta duøng
• caùc kí töï X, Y, Z,… chæ caùc ñaïi löôïng ngaãu nhieân.
• caùc kí töï x, y, z,… chæ giaù trò cuûa caùc ñaïi löôïng ngaãu nhieân.
1.2. Phaân loaïi. Ta chia ñaïi löôïng ngaãu nhieân thaønh hai loaïi:
1) Loaïi rôøi raïc: Laø loaïi ñaïi löôïng ngaãu nhieân chæ nhaän höõu haïn
hoaëc voâ haïn ñeám ñöôïc caùc giaù trò.
Ví duï. Tieán haønh n thí nghieäm. Goïi X laø soá thí nghieäm thaønh coâng.
Khi ñoù X laø ñaïi löôïng ngaãu nhieân rôøi raïc chæ nhaän n+1 giaù trò 0; 1;..; n.
2) Loaïi lieân tuïc. Laø loaïi ñaïi löôïng ngaãu nhieân nhaän voâ haïn khoâng
ñeám ñöôïc caùc giaù trò maø thoâng thöôøng caùc giaù trò naøy laáp kín moät ñoaïn
naøo ñoù trong taäp caùc soá thöïc.
Ví duï. Giaû söû nhieät ñoä trong naêm 2007 taïi moät ñòa phöông dao ñoäng
töø 20o C ñeán 33o C. T (oC) laø nhieät ñoä ño ñöôïc taïi ñòa phöông ñoù, ta coù T
laø ñaïi löôïng ngaãu nhieân lieân tuïc nhaän caùc giaù trò treân [20,33].
1.3. Luaät phaân phoái:
1) Tröôøng hôïp rôøi raïc. Vôùi X laø moät ñaïi löôïng ngaãu nhieân rôøi
raïc nhaän caùc giaù trò taêng daàn : x0, x1,…, xn, ta laäp baûng:
X x1 x
2 ................... xn
P p1 p
2 ................... pn
trong ñoù:
• pk = P(X = xk) ≥ 0 vôùi k = 1, 2, …, n.
• n
k
k1
p1
=
=
∑, nghóa laø p1 + p2 +…+ pn = 1.
2
Ta goïi baûng treân laø Luaät phaân phoái cuûa ñaïi löôïng ngaãu nhieân X. Töø luaät
phaân phoái cuûa X ta coù theå tính xaùc suaát ñeå X nhaän caùc giaù trò treân moät
taäp cho tröôùc, chaúng haïn vôùi i < j ta coù:
P(xi ≤ X ≤ xj) = pi +…+ pj = j
k
ki
p.
=
∑
Ngoaøi ra caùc bieán coá A0 = “X = x1”, A2 = “X = x2”,..., An = “X = xn” taïo
thaønh moät heä ñaày ñuû, xung khaéc töøng ñoâi.
Ví duï. Moät loâ haøng chöùa 10 saûn phaåm, trong ñoù coù 6 saûn phaåm toát
vaø 4 saûn phaåm xaáu. Choïn ngaãu nhieân töø loâ haøng ra 2 saûn phaåm. Goïi X
laø soá saûn phaåm toát coù trong 2 saûn phaåm choïn ra. Tìm luaät phaân phoái
cuûa X.
Giaûi. Ta thaáy X laø ñaïi löôïng ngaãu nhieân rôøi raïc coù theå nhaän caùc giaù trò
laø 0, 1, 2. Aùp duïng coâng thöùc tính xaùc suaát löïa choïn ta ñöôïc:
.
3
1
)2(
;
15
8
)1(
;
15
2
)0(
2
10
0
4
2
6
2
2
10
1
4
1
6
1
2
10
2
4
0
6
0
====
====
====
C
CC
C
CC
C
CC
XPp
XPp
XPp
Vaäy luaät phaân phoái cuûa X laø
X 0 1 2
P 2/15 8/15 1/3
2) Tröôøng hôïp lieân tuïc. Tröôøng hôïp X lieân tuïc, thay cho vieäc lieät
keâ caùc giaù trò cuûa X ôû doøng treân, ta chæ ra ñoaïn [a,b] maø X nhaän giaù trò ô
ûñoaïn ñoù (a, b coù theå höõu haïn hoaëc voâ haïn). Coøn thay cho xaùc suaát p0, p1,…,
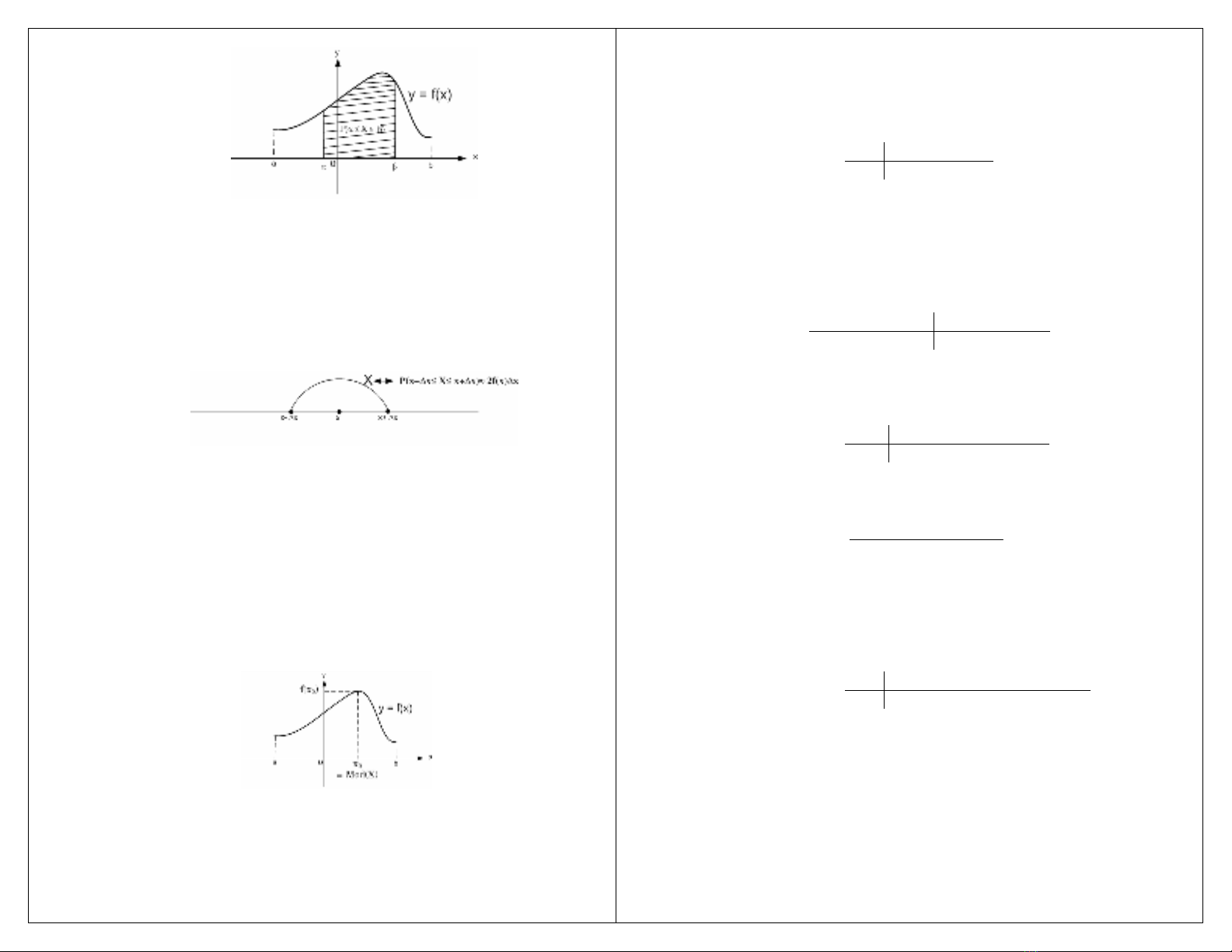
pn ta ñöa ra haøm maät ñoä f(x) [f(x) töông öùng vôùi P(X = x)] thoaû caùc tính
chaát sau:
• f(x) ≥ 0 vôùi moïi x ∈[a,b].
• ∫=
b
a
dxxf .1)(
• ∫
=≤≤
β
α
βα
.)()( dxxfXP
Printed with FinePrint trial version - purchase at www.fineprint.com
3
Töø ñònh nghóa cuûa haøm maät ñoä ta thaáy vôùi Δx khaù beù ta coù heä thöùc xaáp
xæ:
P(x - Δx ≤ X ≤ x + Δx) ≈ 2f(x)Δx.
Thaät vaäy, khi Δx khaù beù ta coù:
xx xx xx
xx xx xx
P(x x X x x) f (t)dt f (x)dt f (x) dt 2f (x) x.
+Δ +Δ +Δ
−Δ −Δ −Δ
−Δ ≤ ≤ +Δ = ≈ ≈ ≈ Δ
∫∫ ∫
Nhö vaäy, vôùi Δx khoâng ñoåi thì xaùc suaát ñeå X laáy giaù trò thuoäc
[x-Δx ; x+Δx ] tæ leä vôùi f(x):
Ñieàu naøy cho thaáy taïi ñieåm x naøo maø giaù trò cuûa haøm f(x) lôùn hôn thì ôû
laân caän cuûa ñieåm ñoù seõ taäp trung moät xaùc suaát lôùn hôn, nghóa laø X nhaän
nhieàu giaù trò trong laân caän ñieåm ñoù hôn. Chính vì theá maø haøm f(x) coù
teân laø haøm maät ñoä.
§2. Caùc ñaëc soá cuûa ñaïi löôïng ngaãu nhieân
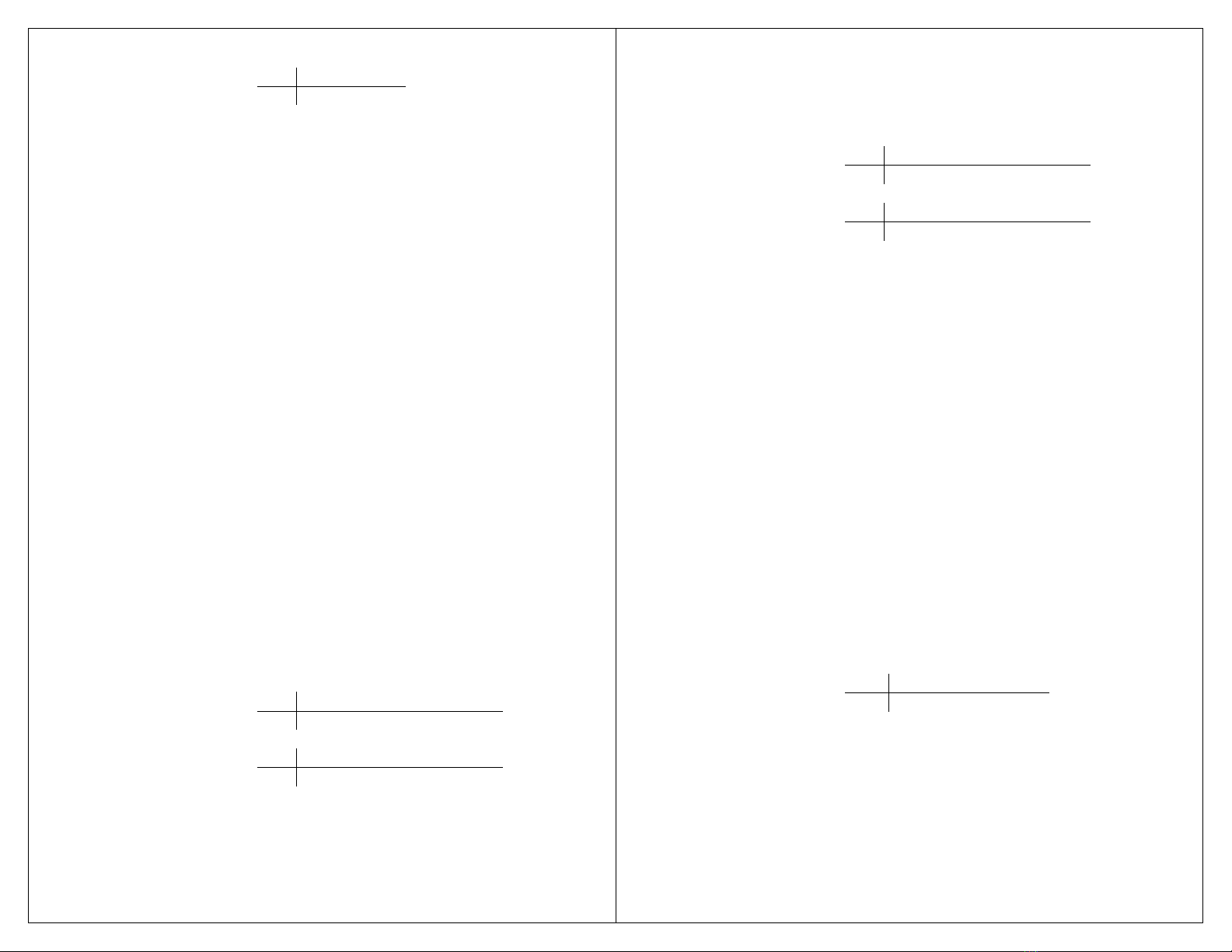
2.1. Mode. Mode cuûa ñaïi löôïng ngaãu nhieân X, kí hieäu Mod(X), laø giaù
trò x0 cuûa X ñöôïc xaùc ñònh nhö sau:
• Neáu X rôøi raïc thì x0 laø giaù trò maø xaùc suaát P(X = x0) lôùn nhaát trong
soá caùc xaùc suaát P(X = x).
• Neáu X lieân tuïc thì x0 laø giaù trò maø haøm maät ñoä f(x) ñaït giaù trò lôùn
nhaát.
4
Nhö vaäy, Mod(X) laø giaù trò tin chaéc nhaát cuûa X, töùc laø giaù trò maø X
thöôøng laáy nhaát. Chuù yù raèng Mod(X) coù theå nhaän nhieàu giaù trò khaùc
nhau.
Ví duï. Xeùt laïi ví duï treân, ta coù
X 0 1 2
P 2/15 8/15 1/3
Do ñoù Mod(X) = 1.
2.2. Kyø voïng
1) Ví duï minh hoïa. Tröôùc khi ñöa ra ñònh nghóa veà kyø voïng, ta
xeùt moät ví duï minh hoaï nhö sau: Moät lôùp hoïc 100 sinh vieân thi moân Anh
vaên vôùi keát quaû nhö sau:
Ñieåm 4 5 7 8
Soá sinh vieân 15 30 35 20
Nhö vaäy, neáu goïi X laø ñieåm moân Anh vaên cuûa moät sinh vieân trong lôùp,
ta thaáy X laø ñaïi luôïng ngaãu nhieân rôøi raïc coù luaät phaân phoái nhö sau:
X 4 5 7 8
P 0,15 0,3 0,35 0,2
Soá thöïc M(X) = 4.0,15 + 5.0,3 + 7.0,35 + 8.0,2 = 6,15 ñöôïc goïi laø kyø
voïng cuûa X. Chuù yù raèng ta coù theå vieát:
100
20.835.730.515.4
)(
+
+
+
=XM
Vaäy kyø voïng M(X) chính laø ñieåm trung bình moân Anh vaên cuûa lôùp treân.
Ví duï treân minh hoaï cho ñònh nghóa toång quaùt sau:
2) Ñònh nghóa. Kyø voïng cuûa ñaïi löôïng ngaãu nhieân X, kí hieäu M(X),
laø soá thöïc ñöôïc xaùc ñònh nhö sau:
• Neáu X rôøi raïc coù luaät phaân phoái
•
X x1 x
2 ……………………….. xn
P p1 p
2 …………………………. pn
thì n
kk
k1
M(X) x p
=
=∑, nghóa laø M(X) = x1p1 + x2p2+…+ xnpn.
• Neáu X lieân tuïc vôùi haøm maät ñoä f(x) coù mieàn xaùc ñònh [a,b] thì
∫
=b
adxxxfXM .)()(
Printed with FinePrint trial version - purchase at www.fineprint.com
5
Ví duï. Xeùt laïi ví duï ñaõ xeùt ôû treân, ta coù X coù phaân phoái nhö sau:
X 0 1 2
P 2/15 8/15 1/3
Do ñoù kyø voïng cuûa X laø
M(X) = 0.2/15 + 1.8/15 + 2.1/3 = 1,2.
3) YÙ nghóa cuûa kyø voïng. Kyø voïng cuûa ñaïi löôïng ngaãu nhieân X laø
giaù trò trung bình (tính theo xaùc suaát) cuûa X. Ñoù laø taâm ñieåm cuûa phaân
phoái maø caùc giaù trò cuûa X ñöôïc phaân boá xung quanh.
4) Tính chaát. Kyø voïng coù caùc tính chaát sau:
4.1. Tính chaát 1. Kyø voïng cuûa moät ñaïi löôïng ngaãu nhieân haèng baèng
chính haèng soá ñoù, nghóa laø:
M(C) = C
(C: Const).
4.2. Tính chaát 2. Vôùi α laø haèng soá ta coù M(αX) = αM(X).
4.3. Tính chaát 3. Kyø voïng cuûa toång hai ñaïi löôïng ngaãu nhieân baèng
toång cuûa hai kyø voïng thaønh phaàn, nghóa laø:
M(X + Y) = M(X) + M(Y).
4.4. Tính chaát 4. Kyø voïng cuûa tích hai ñaïi löôïng ngaãu nhieân ñoäc laäp
baèng tích cuûa hai kyø voïng thaønh phaàn (X, Y ñoäc laäp khi vôùi moïi x, y, caùc
bieán coá “X = x” vaø “Y = y” ñoäc laäp), nghóa laø:
M(XY) = M(X)M(Y).
vôùi moïi X, Y ñoäc laäp.
5) Chöùng minh.
Tính chaát 1. Ñaïi löôïng ngaãu nhieân haèng C chæ nhaän moät giaù trò laø
C vôùi xaùc suaát baèng 1. Do ñoù M(C) = C.1 = C.
Tính chaát 2. Giaû söû X coù phaân phoái nhö sau:
X x1 x
2 ……………………….. xn
P p1 p
2 …………………………. pn
Khi ñoù, vôùi α laø haèng soá, αX coù phaân phoái nhö sau:
αX αx1 αx2 ……………………….. αxn
P p1 p
2 …………………………. pn
6
Suy ra kyø voïng cuûa αX laø:
nn
kk kk
k1 k1
M( X) x p x p M(X).
==
α= α =α =α
∑∑
Tính chaát 3. Giaû söû X, Y coù phaân phoái nhö sau:
X x1 x
2 ……………………….. xn
P p1 p
2 …………………………. pn
Y y1 y
2 ……………………….. ym
P q1 q
2 …………………………. qm
Khi ñoù, X + Y nhaän caùc giaù trò xi + yj. Ñaët pij = P(X = xi, Y = yj). Ta coù
pi = P(X = xi) = P(Y = y1)P(X = xi/Y = y1)+...+ P(Y = ym)P(X = xi/Y = ym)
= P(X = xi ,Y = y1)+...+ P(X = xi , Y = ym) = pi1+...+pim.
Nhö vaäy m
iij
j1
pp
=
=∑ vaø töông töï, n
jij
i1
qp
=
=∑. Suy ra:
nm nm nm n m m n
i j ij i ij j ij i ij j ij
i1j1 i1j1 i1j1 i1 j1 j1 i1
nm
ii jj
i1 j1
M(X Y) (x y )p x p y p x p y p
x p y q M(X) M(Y)
== == == = = = =
==
+= + = + = +
=+=+
∑∑ ∑∑ ∑∑ ∑ ∑ ∑ ∑
∑∑
Tính chaát 4. Giaû söû X, Y ñoäc laäp vaø coù phaân phoái nhö trong chöùng
minh tính chaát 3. Khi ñoù:
pij = P(X = xi, Y = yj) = P(X = xi)P(Y = yj) = piqj.
Suy ra:
nm nm n n
ij ij ij ij ii jj
i1j1 i1j1 i1 i1
M(XY) (x y )p (x y )p q x p y q M(X)M(Y)
== == = =
⎛⎞⎛⎞
== = =
⎜⎟⎜⎟
⎝⎠⎝⎠
∑∑ ∑∑ ∑ ∑ .
2.3. Phöông sai vaø ñoä leäch chuaån.
1) Ví duï minh hoïa. Tröôùc khi ñöa ra ñònh nghóa veà phöông sai, ta
xeùt moät ví duï minh hoaï nhö sau: Xeùt laïi ví duï X laø ñieåm moân Anh vaên
cuûa sinh vieân trong lôùp vôùi luaät phaân phoái nhö sau:
X 4 5 7 8
P 0,15 0,3 0,35 0,2
Ta muoán ñöa ra moät soá ñeå ñaùnh giaù möùc ñoä ñoàng ñeàu veà ñieåm moân
Anh vaên cuûa sinh vieân trong lôùp. Ta ñaõ bieát ñieåm trung bình moân Anh
vaên cuûa lôùp laø μ = M(X) = 6,15. Nhö vaäy ñoä leäch veà ñieåm moân Anh vaên
so vôùi ñieåm trung bình naøy laø X - μ coù phaân phoái nhö sau:
Printed with FinePrint trial version - purchase at www.fineprint.com
7
X − μ −2,15 −1,15 0,85 1,85
P 0,15 0,3 0,35 0,2
Moät caùch töï nhieân, moät caâu hoûi ñöôïc ñaët ra laø lieäu raèng ta coù theå choïn soá
nhö yù ñònh treân laø giaù trò trung bình cuûa ñoä leäch X - μ, töùc laø M(X − μ),
ñöôïc hay khoâng? Tuy nhieân qua tính toaùn ta thaáy ngay M(X-μ) = 0 vaø
nhö vaäy roõ raøng khoâng theå choïn M(X − μ) ñeå ñaùnh giaù möùc ñoä ñoàng ñeàu
veà ñieåm moân Anh vaên. Coù theå lyù giaûi vì sao M(X-μ) = 0 nhö sau: Nhöõng
ñieåm treân trung bình vaø nhöõng dieåm döôùi trung bình cuûa sinh vieân trong
lôùp ñaõ trieät tieâu laãn nhau. Ñeå traùnh ñieàu naøy, ta xeùt bình phöông ñoä leäch
(X − μ)2 vôùi luaät phaân phoái nhö sau:
(X − μ)2 (−2,15)2 (−1,15)2 (0,85)2 (1,85)2
P 0,15 0,3 0,35 0,2
vaø choïn soá ñaõ ñònh laø giaù trò trung bình cuûa bình phöông ñoä leäch (X − μ)2,
töùc laø M((X − μ)2):
M((X-μ)2) = (−2,15)20,15 + (−1,15)20,3 + (0,85)20,35 + (1,85)20,2 = 2,0275.
Roõ raøng soá naøy ñaëc tröng cho möùc ñoä ñoàng ñeàu veà ñieåm moân Anh
vaên cuûa sinh vieân trong lôùp, ta goïi soá ñoù laø phöông sai cuûa X. Ví duï treân
minh hoaï cho ñònh nghóa toång quaùt sau:
2) Ñònh nghóa. Phöông sai cuûa ñaïi löôïng ngaãu nhieân X, kí hieäu
D(X), laø soá thöïc khoâng aâm ñònh bôûi:
D(X) = M((X − μ)2),
trong ñoù μ = M(X) laø kyø voïng cuûa X. Caên baäc hai cuûa phöông sai ñöôïc
goïi laø ñoä leäch chuaån, kí hieäu )(
X
σ
. Vaäy
)()( XDX =
σ
.
3) Coâng thöùc tính phöông sai. Töø ñònh nghóa cuûa phöông sai ta
coù coâng thöùc khaùc ñeå tính phöông sai nhö sau:
22
D(X) = M(X ) [M(X)]−
trong ñoù M(X2), M(X) laàn löôït laø kyø voïng cuûa X2 vaø X. Nhö vaäy,
• Neáu X rôøi raïc coù luaät phaân phoái
8
X x1 x
2 ……………………….. xn
P p1 p
2 …………………………. pn
thì coâng thöùc treân trôû thaønh
nn
22
kk kk
k1 k1
D(X) x p ( x p )
==
=−
∑∑
• Neáu X lieân tuïc vôùi haøm maät ñoä f(x) coù mieàn xaùc ñònh [a,b] thì
bb
22
aa
D(X) x f(x)dx ( xf(x)dx)=−
∫∫
Chöùng minh.
22 22 2
22222222
D(X) M[(X ) ] M(X 2 X ) M(X ) M(2 X) M( )
M(X ) 2 M(X) M(X ) 2 M(X ) M(X ) [M(X)]
=−μ=−μ+μ= −μ+μ
=−μ+μ=−μμ+μ=−μ=−
Ví duï. Xeùt laïi ví duï ñaõ xeùt ôû treân, ta coù X coù phaân phoái nhö sau:
X 0 1 2
P 2/15 8/15 1/3
vaø kyø voïng cuûa X laø M(X) = 1,2ø. Suy ra phöông sai cuûa X laø:
D(X) = M(X2) - [M(X)] 2 = 02.2/15 + 12.8/15 + 22.1/3 - (1,2)2 = 32/75
≈ 0,4267.
Ñoä leäch chuaån cuûa X laø:
.6532,04267,0)()( ≈== XDX
σ
4) YÙ nghóa cuûa phöông sai
Ta coù:
• μ = M(X) laø kyø voïng cuûa X.
• X - μ laø ñoä leäch cuûa X so vôùi kyø voïng.
• (X - μ)2 laø bình phöông ñoä leäch cuûa X so vôùi kyø voïng.
• D(X) = M((X - μ)2) giaù trò trung bình cuûa bình phöông ñoä leäch cuûa
X so vôùi kyø voïng.
Phöông sai cuûa ñaïi löôïng ngaãu nhieân X chính laø giaù trò trung bình
cuûa bình phöông ñoä leäch giöõa caùc giaù trò cuûa X vaø taâm ñieåm kyø voïng.
Phöông sai phaûn aùnh möùc ñoä ñoàng ñeàu vaø söï phaân boá caùc giaù trò cuûa X
xung quanh giaù trò kyø voïng. Neáu phöông sai nhoû thì nhieàu giaù trò cuûa X
taäp trung gaàn kyø voïng, coøn neáu phöông sai lôùn thì nhieàu giaù trò cuûa X
phaân taùn xa kyø voïng.
Printed with FinePrint trial version - purchase at www.fineprint.com
9
Trong thöïc teá, thoâng thöôøng kyø voïng M(X) laø giaù trò qui ñònh, chaúng
haïn ñöôøng kính qui ñònh, troïng löôïng qui ñònh,… Coøn thöïc teá saûn xuaát ra
laø ñaïi löôïng ngaãu nhieân X. Do ñoù, trong coâng nghieäp, phöông sai bieåu thò
ñoä chính xaùc cuûa saûn xuaát. Trong chaên nuoâi, phöông sai bieåu thò möùc ñoä
ñoàng ñeàu cuûa ñaøn gia suùc,… Trong troàng troït, phöông sai bieåu thò möùc ñoä
oån ñònh cuûa naêng suaát caây troàng,…
5) Tính chaát. Phöông sai coù caùc tính chaát sau:
Tính chaát 1. Phöông sai cuûa moät ñaïi löôïng ngaãu nhieân haèng baèng
0, nghóa laø:
D(C) = 0
(C: Const).
Tính chaát 2. Vôùi α laø haèng soá ta coù
D(αX) = α2(D(X).
Tính chaát 3. Phöông sai cuûa toång hai ñaïi löôïng ngaãu nhieân ñoäc laäp
baèng toång cuûa hai phöông sai thaønh phaàn, nghóa laø:
D(X + Y) = D(X) + D(Y).
vôùi moïi X, Y ñoäc laäp.
Chöùng minh.
Tính chaát 1. D(C) = M(C2) – [M(C)]2 = C2 – C2 = 0.
Tính chaát 2. Ta coù:
D(αC) = M(α2C2) – [M(αC)]2 = α2M(C2) – [αM(C)]2
= α2M(C2) – α2[M(C)]2 = α2(M(C2) – [M(C)]2) = α2D(C)
Tính chaát 3. Vôùi X, Y ñoäc laäp, ta coù:
D(X + Y) = M[(X+Y)2] – M[(X+Y)]2 = M(X2 + 2XY + Y2] – [M(X) + M(Y)]2
= M(X2 ) + M(2XY) + M(Y2) – ([M(X)]2 + 2M(X)M(Y) + [M(Y)]2)
= M(X2 ) + 2M(Y)M(Y)+ M(Y2) – [M(X)]2 - 2M(X)M(Y) - [M(Y)]2
= M(X2 ) – [M(X)]2 + M(Y2) - [M(Y)]2 = D(X) + D(Y)
2.4 Söû duïng maùy tính ñeå tính caùc ñaëc soáù. Ta coù theå söû duïng phaàn
meàm thoáng keâ trong caùc maùy tính boû tuùi CASIO 500MS, 570MS, 500ES,
10
570ES,...) ñeå tính kyø voïng, phöông sai vaø ñoä leäch chuaån cuûa ñaïi löôïng ngaãu
nhieân rôøi raïc.
Ví duï. Xeùt ñaïi löôïng ngaãu nhieân rôøi raïc X coù phaân phoái nhö sau:
X 0 1 2
P 2/15 8/15 1/3
a) Ñoái vôùi loaïi maùy tính CASIO 500 vaø 570MS:
1) Vaøo MODE SD: Baám MODE (vaøi laàn...) vaø baám soá öùng vôùi SD, treân maøn
hình seõ hieän leân chöõ SD.
2) Xoùa boä nhôù thoáng keâ: Baám SHIFT MODE 1 (maøn hình hieän leân Stat
clear) AC =. Kieåm tra laïi: Baám nuùt troøn
∇
hoaëc Δ thaáy n = vaø ôû goùc soá 0
laø ñaõ xoùa.
3) Nhaäp soá lieäu: Baám +
xi SHIFT , pi M (khi baám SHIFT , treân maøn
hình hieän leân daáu ;). Cuï theå, ta baám:
b/c +
b/c +
b/c +
0 SHIFT , 2 a 1 5 M
1 SHIFT , 8 a 1 5 M
2 SHIFT , 1 a 3 M
4) Kieåm tra vaø söûa soá lieäu sai: Baám nuùt troøn ∇ ñeå kieåm tra vieäc nhaäp soá
lieäu. Thaáy soá lieäu naøo sai thì ñeå maøn hình ngay soá lieäu ñoù, nhaäp soá lieäu ñuùng
vaø baám = thì soá lieäu môùi seõ thay cho soá lieäu cuõ.
Ví duï. Nhaäp sai b/c +
0 SHIFT , 2 a 2 5 M . Khi kieåm tra ta thaáy
treân maøn hình hieän ra:
- x1 = 0 (ñuùng).
- Freq1 = 2/25 (sai)
Söûa nhö sau: Ñeå maøn hình ôû Freq1 = 2/25, baám b/c
2 a 1 5 =
thì nhaän ñöôïc soá lieäu ñuùng Freq1 = 2/15.
Soá lieäu naøo bò nhaäp dö thì ñeå maøn hình ôû soá lieäu ñoù vaø baám
+
SHIFT M thì toøan boä soá lieäu ñoù (goàm giaù trò cuûa X vaø xaùc suaát töông öùng)
seõ bò xoùa. Chaúng haïn, nhaäp dö b/c +
3 SHIFT , 3 a 4 M . Khi kieåm tra ta
thaáy x4 = 3 (dö). Ta ñeå maøn hình ôû soá lieäu ñoù vaø baám +
SHIFT M thì toøan boä
soá lieäu dö (goàm giaù trò cuûa X = 3 vaø xaùc suaát töông öùng 3/4) seõ bò xoùa.
Chuù yù. Sau khi kieåm tra vieäc nhaäp soá lieäu xong, phaûi baám
A
C ñeå
xoùa maøn hình vaø thoùat khoûi cheá ñoä chænh söûa.
5) Ñoïc keát quaû:
Printed with FinePrint trial version - purchase at www.fineprint.com


























