Bài giảng: Xửlý sốtín hiệu
5/22/2010
1
Chương 5
BIẾN ĐỔI Z
Nội dung:
5.1 Biến đổi Z
5.1.1 Định nghĩa biến đổi Z
5.1.2 Các tính chất của biến đổi Z
5.1.3 Giản đồ cực-không
5.2 Biến đổi Z ngược
5.2.1 Phương pháp phân tích thành chuỗi lũy thừa
5.2.2 Phương pháp phân tích thành phân thức sơ cấp
5.3 Phân tích hệthống dùng biến đổi Z
Bài tập
Bài giảng: Xửlý sốtín hiệu
2
Chương 5 BIẾN ĐỔI Z
5.1 Biến đổi Z:
¾là phép chuyển tín hiệu sang miền Z để thuận tiên trong phân tích, xửlý.
¾biến đổi Z có vai trò như phép biến đổi Laplace trong mạch tương tự.
¾ được dùng để tính toán đáp ứng của hệthống LTI, thiết kếcác bộlọc,vv...
5.1.1 Định nghĩa:
¾Biến đổi Z của một tín hiệu rời rạc x(n):
(z: biến phức)
¾Ký hiệu: hay:
Vùng hội tụcủa biến đổi Z (ROC: Region Of Convergence)
ROC là tập hợp những giá trịcủa Z làm cho X(z) có giá trịhữu hạn.
Phải chỉrỏra khi nói đến biến đổi Z.
5/22/2010
() () n
n
X
zxnz
+∞
−
=−∞
=∑
() ()
Z
x
nXz⎯⎯→
[
]
() ()Xz Zxn=
{
}
|()ROC z X z
=
∈≠∞^
Bài giảng: Xửlý sốtín hiệu
3
Chương 5 BIẾN ĐỔI Z (tt)
5.1 Biến đổi Z (tt):
Ví dụ1: Xác định biến đổi z của các tín hiệu sau
a. x(n) = {1,2,5,7,0,1}
b. x(n) = anu(n)
c. x(n) = -anu(-n-1)
d. x(n) = anu(n) - bnu(-n-1)
Lời giải:
a. Từ định nghĩa:
X(z) = z2+ 2z + 5 + 7z-1+ z-3 ; ROC: z ≠0; z ≠∞
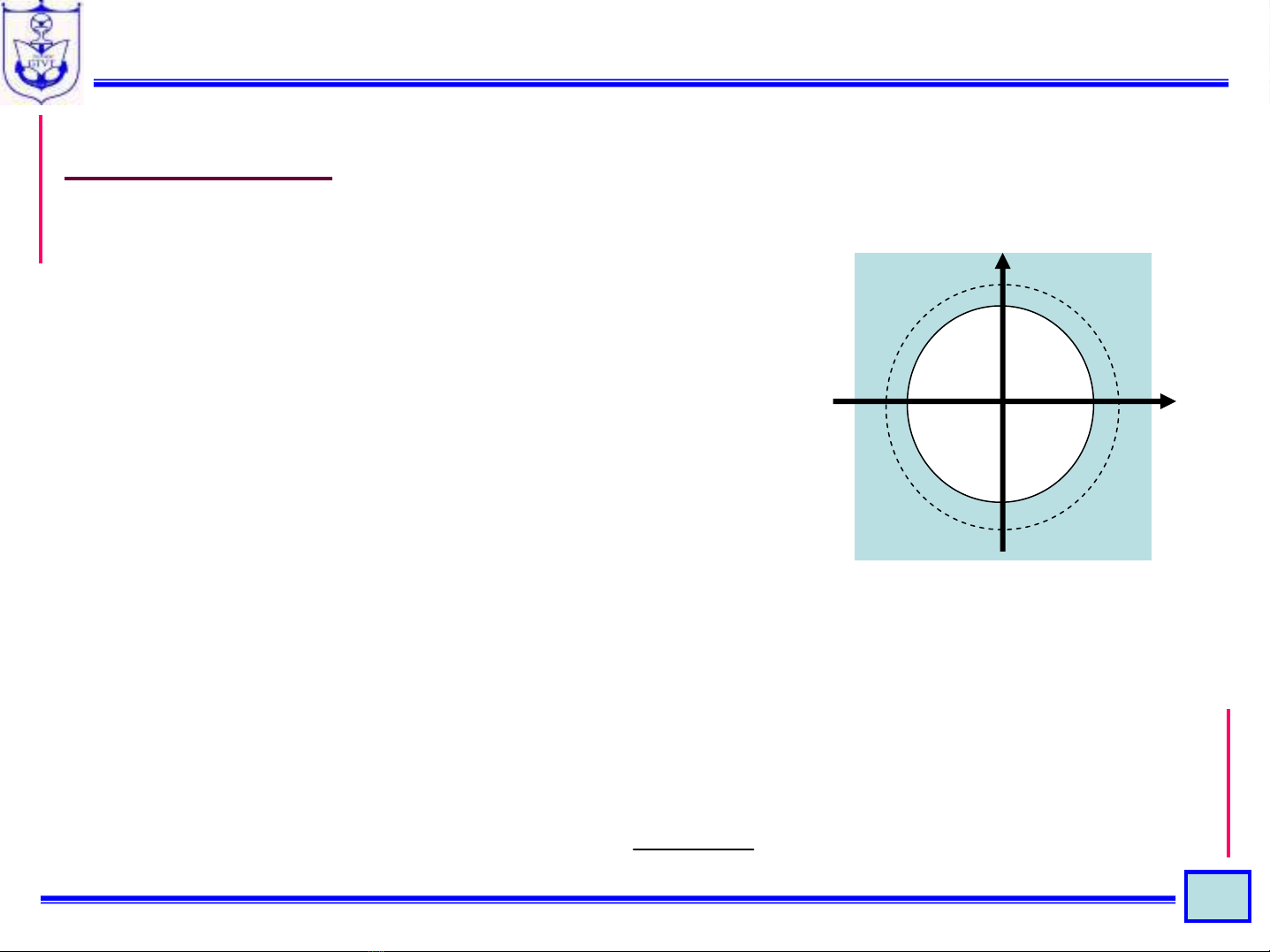
b. Ta có:
Nếu: |az-1|<1Æ|z|>|a| thì:
ROC: |z| > |a|
5/22/2010
1
00
() () () ( )
nnnnn n
nn nn
Xz xnz aunz az az
+∞ +∞ +∞ +∞
−−−−
=−∞ =−∞ = =
== ==
∑∑ ∑∑
1
1
() 1
Xz az
−
=
-1
ROC
ImZ
01
a
ReZ
Bài giảng: Xửlý sốtín hiệu
4
Chương 5 BIẾN ĐỔI Z (tt)
5.1 Biến đổi Z (tt):
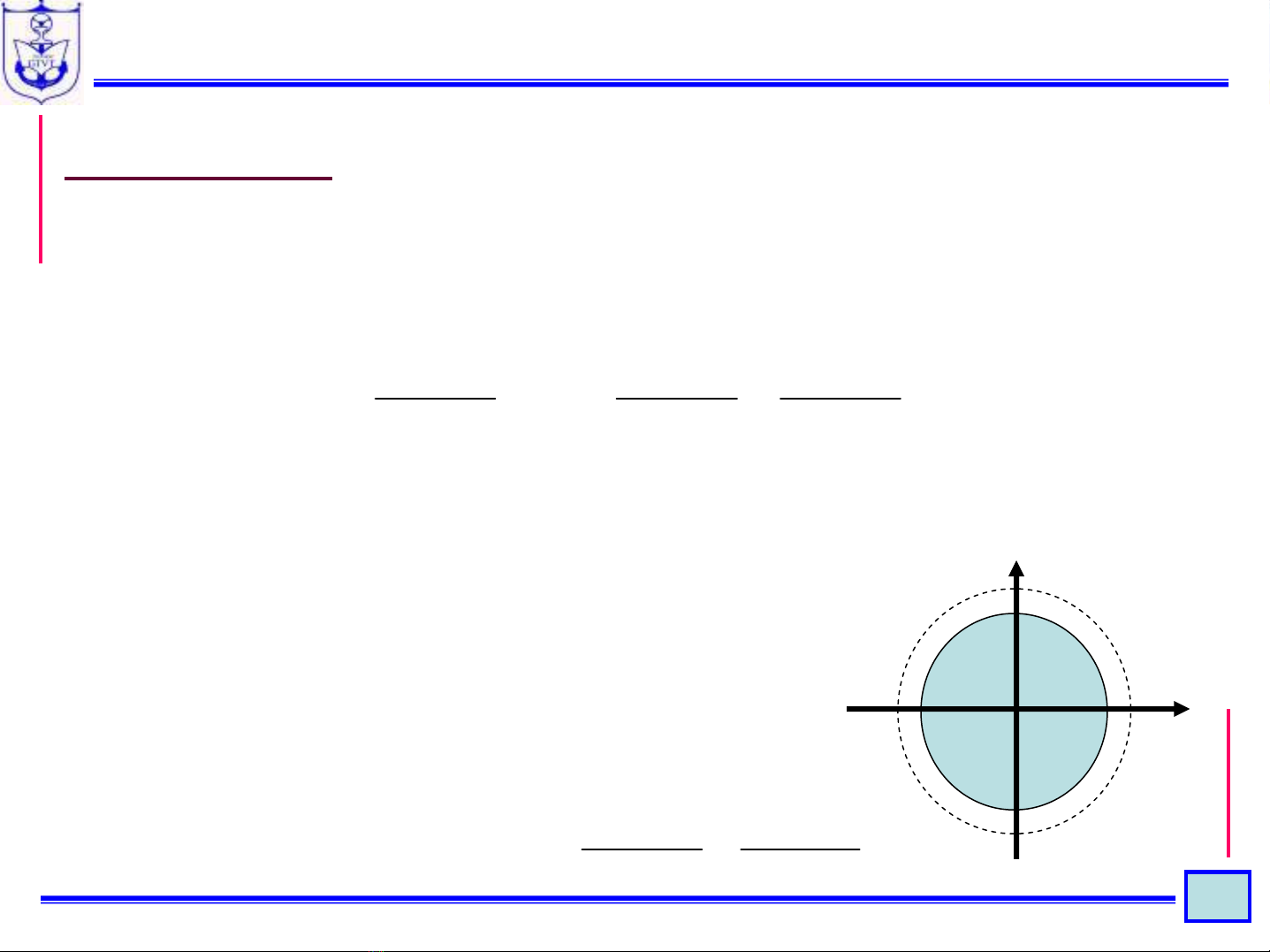
c. Ta có:
Nếu: |a-1z|<1Æ|z|<|a| thì:
ROC: |z| < |a|
d. Ta có:
Nếu |b|<|a|: ROC = {Ø}:
Ækhông tồn tại X(z).
Nếu |b|>|a|: ROC : |a|<|z|<|b|:
5/22/2010
11 1
1
() () ( )
nnnnn n
nnn n
X
zxnz az az az
+∞ − +∞
−−−−
=−∞ =−∞ =∞ =
==−=−=−
∑∑∑∑
1
111
11
() 1
111
az
Xz az a z az
−
−
−−
=− + =− =
−
−−
1
0
01
() () nnn nn
nnn
nn nn
nn
X
zxnzaz bz
az b z
+∞ +∞ −
−
−−
=−∞ = =−∞
+∞ ∞
−−
==
==−
=−
∑∑∑
∑∑
11
11
() 11
Xz az bz
−
−
=+
−
−
-1
ImZ
01
a
ReZ
ROC
Bài giảng: Xửlý sốtín hiệu
5
Chương 5 BIẾN ĐỔI Z (tt)
5.1 Biến đổi Z (tt):
Một sốcặp biến đổi Z thông dụng:
5/22/2010