http://www.ebook.edu.vn 1
®¸p ¸n
Ngµnh ®µo t¹o: §iÖn tö – viÔn th«ng
HÖ ®µo t¹o : §¹i häc
M«n häc : Lý thuyÕt th«ng tin M· sè 411 LTT 340A Sè §VHT: 4
PhÇn 1: lý thuyÕt th«ng tin
C©u 1: (1 ®iÓm): §Þnh nghÜa l−îng th«ng tin riªng (®é bÊt ®Þnh) cña mét biÕn
ngÉu nhiªn. X¸c ®Þnh c¸c ®¬n vÞ ®o
- §Þnh nghÜa l−îng th«ng tin riªng (®é bÊt ®Þnh)
L−îng th«ng tin riªng lµ ®é bÊt ®Þnh tiÒm n¨ng chøa trong mét biÕn cè ngÉu
nhiªn k
x
.
Ký hiÖu
(
)
k
I
x
(
)
(
)
kk
Iklnp
x
x
=
- C¸c ®¬n vÞ ®o
k1=−
()
(
)
kk
Ilnp
x
=
− (nat)
1
kln 2
=−
()
(
)
k2k
Ilogp
x
x
=
− (bÝt)
1
kln10
=−
(
)
(
)
kk
Ilgp
x
x
=
− (hart)
1 nat = 1,443 bÝt
1 hart = 3,322 bÝt
C©u 2: (1 ®iÓm) §Þnh nghÜa entropy cña nguån rêi r¹c
Entropy cña nguån tin rêi r¹c A lµ trung b×nh thèng kª cña l−îng th«ng tin
riªng cña c¸c tin thuéc A
Ký hiÖu:
()
1
HA
() ()
1i
HA MIa
Δ
=
⎡
⎤
⎣
⎦
() () ()
12 s
12 s
aa...a
Apa pa ... pa
⎛⎞
=⎜⎟
⎝⎠
(
)
i
0pa 1≤≤
()
s
i
i1
pa 1
=
=
∑
() () ()
s'
1ii
i1
HA palogpa
=
=−
∑ (bÝt)
http://www.ebook.edu.vn 2
C©u 3: (1 ®iÓm) Nªu c¸c tÝnh chÊt cña entropy cña nguån rêi r¹c
C¸c tÝnh chÊt cña
()
1
HA
- Khi
()
k
pa 1=,
()
i
pa 0= víi ik
∀
≠ th×
(
)
(
)
11
min
HA HA 0
=
=
- Mét nguån tin rêi r¹c gåm s dÊu ®ång x¸c suÊt cho entropy cùc ®¹i. Ta cã
(
)
1max
HA logs=
- Entropy cña nguån rêi r¹c lµ mét ®¹i l−îng giíi néi
(
)
1
0 H a logs≤≤
C©u 4: (1 ®iÓm) §Þnh nghÜa kh¶ n¨ng th«ng qua kªnh rêi r¹c, nªu c¸c tÝnh chÊt?
- §Þnh nghÜa: Kh¶ n¨ng th«ng qua cña kªnh rêi r¹c lµ gi¸ trÞ cùc ®¹i cña l−îng
th«ng tin chÐo trung b×nh truyÒn qua kªnh trong mét ®¬n vÞ thêi gian lÊy theo
mäi kh¶ n¨ng cã thÓ cã cña nguån tin A.
() ()
''
k
AA
C max I A,B v max I A, B
Δ
== (bps)
- C¸c tÝnh chÊt:
+ '
C0≥
'
C0= khi A vµ B lµ ®éc lËp (kªnh bÞ ®øt)
+ '
k
Cvlogs≤
'
k
Cvlogs= khi kªnh kh«ng nhiÔu
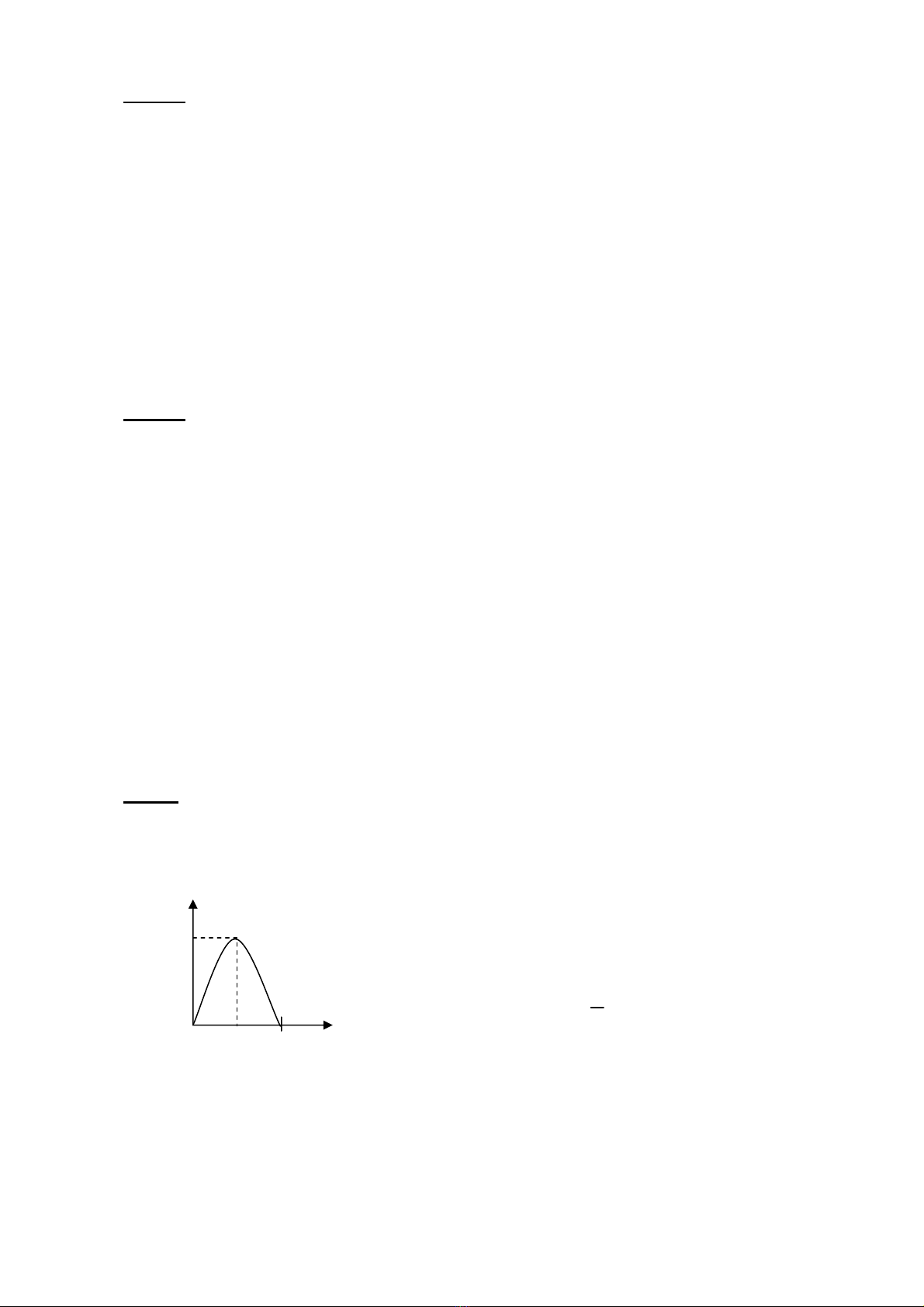
C©u 5: (2 ®iÓm) Entropy cña nguån rêi r¹c nhÞ ph©n. ý nghÜa cña d¬n vÞ ®o bÝt?
- Entropy cña nguån rêi r¹c nhÞ ph©n.
12
aa
Ap1p
⎛⎞
=⎜⎟
−
⎝⎠
(
)
(
)
(
)
1max
H A plog p 1 p log 1 p
=
−−− −
Khi 1
p1p 2
=
−=
(
)
(
)
11
max
HA HA 1bit
=
=
- ý nghÜa: 1 bÝt lµ l−îng th«ng tin riªng trung b×nh chøa trong mét biÕn cè cña
mét nguån rêi r¹c 2 ph©n ®ång x¸c suÊt.
()
1
HA
(bits)
p
0
,
5 1
1
http://www.ebook.edu.vn 3
C©u 6: (2 ®iÓm) X¸c ®Þnh hai tr¹ng th¸i cùc ®oan cña kªnh rêi r¹c.
- Kªnh bÞ ®øt:
C¸c nguån tin A vµ B ë hai ®Çu thu vµ ph¸t lµ ®éc lËp.
()
(
)
ij i
pa b pa=
(
)
(
)
ji i
pb a pa=
(
)
(
)
(
)
ij i j
pab pa pb=
Ta cã:
(
)
(
)
j
HAb HA=
()
(
)
HAB HA
=
NhËn xÐt: L−îng th«ng tin tæn hao trung b×nh ®óng b»ng entropy cña
nguån. Kªnh kh«ng thÓ truyÒn tin ®−îc
- Kªnh kh«ng nhiÔu:
AB≡
()
kk
pa b 1
=
(
)
k
HAb 0
=
()
HAB 0
=
NhËn xÐt: L−îng th«ng tin tæn hao trªn kªnh b»ng 0
C©u 7: (2 ®iÓm) Entropy cã ®iÒu kiÖn
(
)
HAB: ®Þnh nghÜa vµ nªu c¸c tÝnh chÊt
- §Þnh nghÜa: Entropy cã ®iÒu kiÖn vÒ 1 tr−êng tin A khi ®· râ tr−êng tin B ®−îc
x¸c ®Þnh theo c«ng thøc sau:
()
() ()
st
ij i j
i1 j1
HAB pab logpa b
==
=−
∑∑
- C¸c tÝnh chÊt:
+
(
)
(
)
(
)
(
)
(
)
HAB HA HBA HB HAB=+ =+
+
(
)
(
)
0HAB HA≤≤
+
(
)
(
)
(
)
HAB HA HB=+
C©u 8: (2 ®iÓm) L−îng th«ng tin chÐo trung b×nh truyÒn qua kªnh rêi r¹c: ®Þnh
nghÜa vµ tÝnh chÊt
- §Þnh nghÜa:
()
(
)
ij
IA,B MIa,b
Δ
⎡
⎤
=
⎣
⎦
víi
()
(
)
()
ij
ij
i
pa b
Ia,b log pa
=
http://www.ebook.edu.vn 4
()
()
(
)
()
st ij
ij
i1 j1 i
pa b
IA,B pab log pa
==
=∑∑
(
)
(
)
(
)
(
)
(
)
IA,B HA HAB HB HBA=− =−
- TÝnh chÊt:
+
(
)
IA,B 0≥
+
(
)
(
)
IA,B HA≤
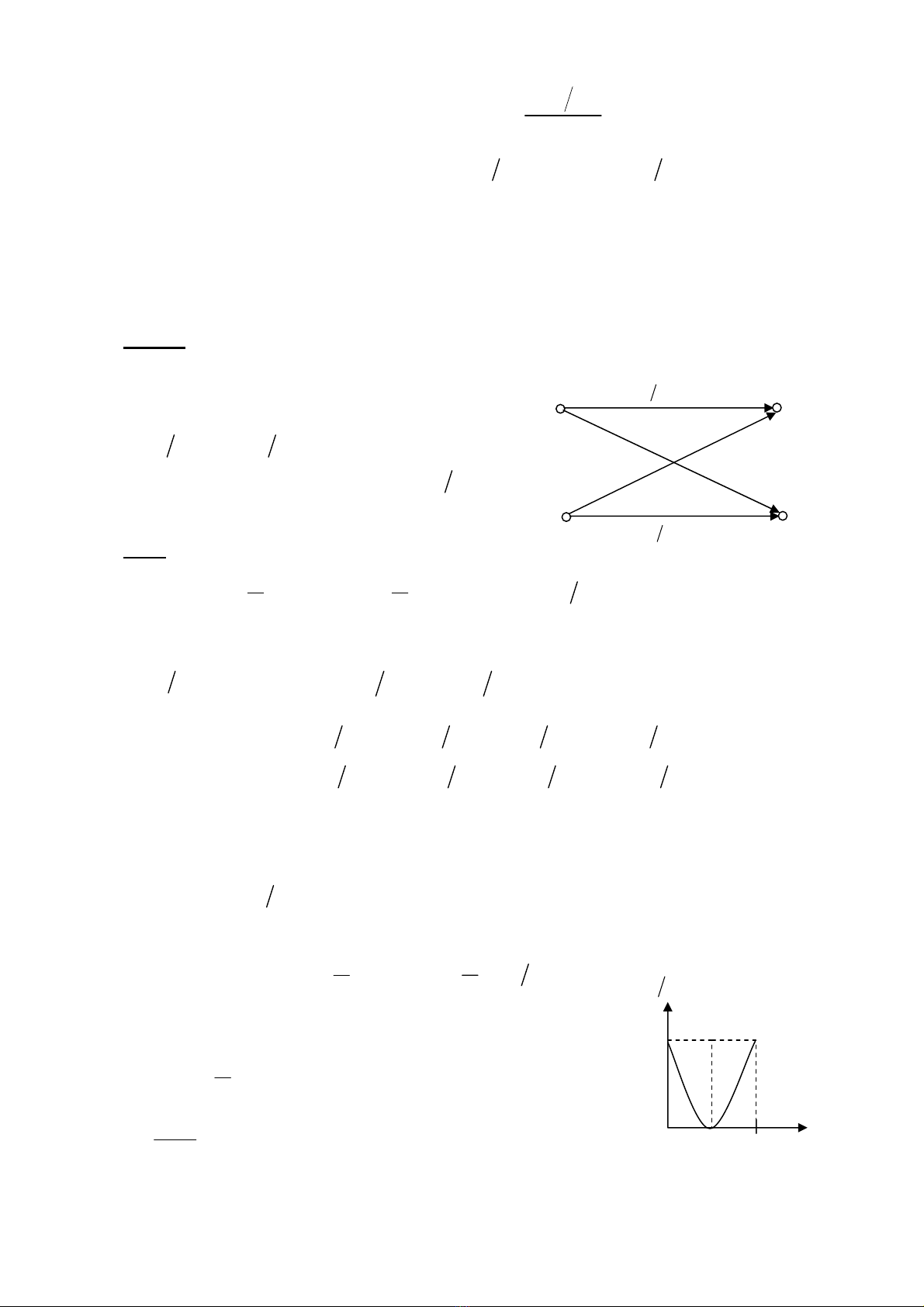
C©u 9: (3 ®iÓm) Cho kªnh ®èi xøng nhÞ ph©n sau
()
1
p
ap=
(
)
21
p
ap
=
−
(
)
(
)
12 21 1
s
d
p
ba pb a p p=−=−
Cho tèc ®é truyÒn tin cña kªnh 1
k
vT
=
TÝnh kh¶ n¨ng th«ng qua '
C cña kªnh nµy.
Gi¶i:
Ta cã
() () ()
'
AA
11
CmaxIA,B maxHBHBA
TT
==−
⎡
⎤
⎣
⎦
Trong ®ã:
() ()
()()
() ()()()()
()()()()()
()() () ()()
()()
2t
iji ji
i1 j1
111 11 21 21
212 12 22 22
s sss ss s s
ss s s
HBA pa pb a logpb a
pa pbalogpba pbalogpba
pa pbalogpba pbalogpba
p 1 p log 1 p p logp 1 p p log p 1 p log 1 p
plogp 1 p log1 p
==
=−
=− + −⎡⎤
⎣⎦
−+
⎡⎤
⎣⎦
=−−−+ −− +−−
⎡⎤⎡⎤
⎣⎦⎣⎦
=− + − −
⎡⎤
⎣⎦
∑∑
Ta thÊy
(
)
HBA kh«ng phô thuéc vµo x¸c suÊt tiªn nghiÖm cña c¸c tin thuéc
nguån A. Do ®ã:
() ()
'
A
11
C maxHB HBA
TT
=−
Ta cã
(
)
(
)
max
A
max H B H B log 2 1bit===
'
max
1
CT
= khi s
p0= (kªnh kh«ng nhiÔu)
()()
'
ss s s
'
max
C1 p log p 1 p log 1 p
C=+ + − −
2
b
1
b
2
a
1
a
s
p
s
p
(
)
21 d
pb a p=
(
)
12 d
pb a p=
A B
''
max
CC
s
p
0
,
5 1
1
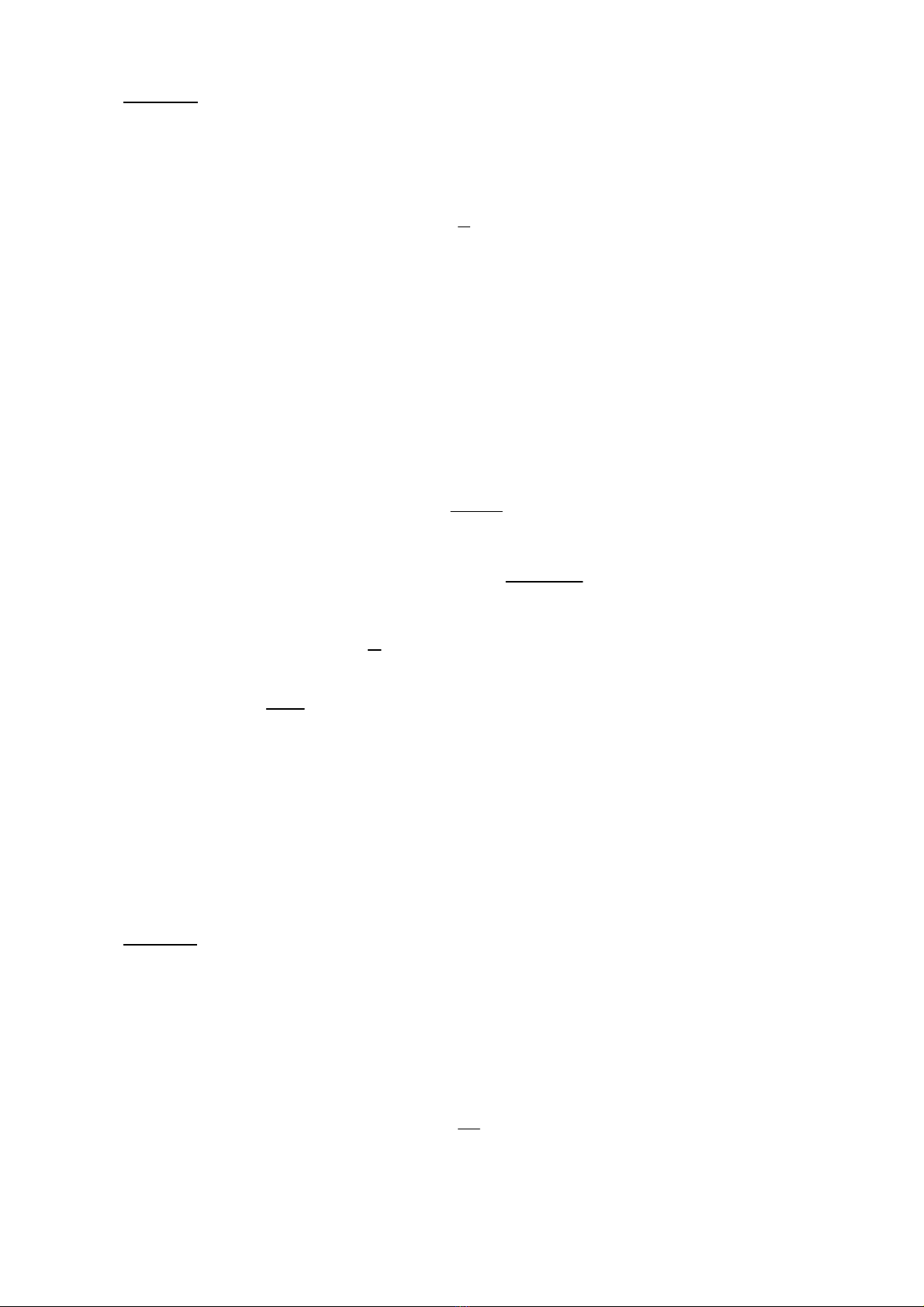
http://www.ebook.edu.vn 5
C©u 10: (3 ®iÓm) A chän ngÉu nhiªn mét trong c¸c sè tõ 0 ®Õn 7. TÝnh sè c©u
hái trung b×nh tèi thiÓu mµ B cÇn ®Æt cho A ®Ó x¸c ®Þnh ®−îc sè mµ A ®· chän.
Nªu thuËt to¸n hái? Gi¶ sö A ®· chän sè 3, h·y ®Æt c¸c c©u hái cÇn thiÕt?
§é bÊt ®Þnh cña sè ®−îc chän ngÉu nhiªn:
() ()
ii
1
Ia logpa log 3bit
8
=− =− =
§Ó t×m ®−îc sè ®· chän cña A, B ph¶i ®Æt c¸c c©u hái cho A ®Ó thu ®−îc ®ñ
mét l−îng th«ng tin cÇn thiÕt lµ 3 bÝt.
Mçi c©u hái cña B (d¹ng lùa chän) cã thÓ xem lµ nguån rêi r¹c nhÞ ph©n, bëi
vËy l−îng th«ng tin nhËn ®−îc sau mçi c©u tr¶ lêi t−¬ng øng lµ:
(
)
(
)
(
)
HB plogp 1 plog1 p=− − − −
Víi p : x¸c suÊt nhËn c©u tr¶ lêi ″®óng ″
1p−: x¸c suÊt nhËn c©u tr¶ lêi ″sai″
VËy sè c©u hái cÇn thiÕt n lµ :
(
)
()
i
Ia
nHB
=
Sè c©u hái trung b×nh tèi thiÓu lµ:
(
)
()
i
min
max
Ia
nHB
=
(
)
max
HB khi 1
p1p 2
=− =
min
3bit
n3
1bit
==
lÇn hái
Gi¶ sö A chän sè B. C¸c c©u hái b cã thÓ ®Æt cho A lµ:
- C©u 1 - Sè A chän lín h¬n 3? Tr¶ lêi: Sai
- C©u 2 - Sè A chän lín h¬n 1? Tr¶ lêi: §óng
- C©u 3 - Sè A chän lín h¬n 2? Tr¶ lêi: Sai
VËy sè A chän lµ 3
C©u 11: (4 ®iÓm) Mét thiÕt bÞ v« tuyÕn ®iÖn gåm 16 khèi cã ®é tin cËy nh− nhau
vµ ®−îc m¾c nèi tiÕp. Ta sö dông mét thiÕt bÞ ®o ®Ó ®o tÝn hiÖu ra cña c¸c khèi.
Gi¶ sö cã mét khèi nµo ®ã bÞ háng. H·y tÝnh sè lÇn ®o trung b×nh tèi thiÓu ®Ó t×m
®−îc khèi bÞ háng. Nªu thuËt to¸n ®o? Gi¶ sö khèi háng lµ khèi thø 6, t×m vÞ trÝ
c¸c ®iÓm ®o cÇn thiÕt?
Theo gi¶ thiÕt ®é bÊt ®Þnh cña khèi háng lµ:
() ()
ii
1
Ia logpa log 4bit
16
=− =− =
L−îng th«ng tin nhËn ®−îc sau mçi phÐp ®o:
(
)
(
)
(
)
HB plogp 1 plog1 p=− − − −