
Tr ng THPT Chuyên L ng Văn Chánh – Phú yênườ ươ
Bài 1: Xác đ nh c ng đ đi n tr ng gây ra b i m t vòng dây d n m nh bán kính R mangị ườ ộ ệ ườ ở ộ ẫ ả
đi n tích q, t i m i đi m M n m trên tr c c a vòng dây, cách tâm O c a vòng dây m tệ ạ ỗ ể ằ ụ ủ ủ ộ
kho ng OM = h.ả
Xét các tr ng h p riêng: đi m M trùng v i tâm O và đi m M r t xa vòng dây (h >> R).ườ ợ ể ớ ể ở ấ
Bài 2: M t vòng dây d n m nh tâm O, bán kính R mang đi n tích Q phân b đ u trên vòngộ ẫ ả ệ ố ề
dây. Ng i ta c t đi t vòng dây m t đo n r t nh l (l << R) sao cho s phân b đi n tíchườ ắ ừ ộ ạ ấ ỏ ự ố ệ
trên vòng v n y nguyên nh tr c. Xác đ nh c ng đ đi n tr ng t i tâm O gây ra b i vòngẫ ư ướ ị ườ ộ ệ ườ ạ ở
dây đã b c t m t đo n khi đó.ị ắ ộ ạ
Bài 3: M t bán c u kim lo i tâm O, đ nh A, bán kính R, mang đi n đi n tích phân b đ u v iộ ầ ạ ỉ ệ ệ ố ề ớ
m t đ đi n tích m t ậ ộ ệ ặ σ. Xác đ nh c ng đ đi n tr ng do bán c u gây ra t i tâm O.ị ườ ộ ệ ườ ầ ạ
Bài 4: Cho đi n tích đi m d ng q = 1nC.ệ ể ươ
a. Đ t đi n tích q t i tâm hình l p ph ng c nh a = 10cm. Tính đi n thông qua t ngặ ệ ạ ậ ươ ạ ệ ừ
m t c a hình l p ph ng đó. N u bên ngoài hình l p ph ng còn có các đi n tích khác thìặ ủ ậ ươ ế ậ ươ ệ
đi n thông qua t ng m t c a hình l p ph ng và qua toàn b hình l p ph ng có thay đ iệ ừ ặ ủ ậ ươ ộ ậ ươ ổ
không?
b. Đ t đi n tích q t i m t đ nh c a hình l p ph ng nói trên. Tính đi n thông qua t ngặ ệ ạ ộ ỉ ủ ậ ươ ệ ừ
m t c a hình l p ph ng.ặ ủ ậ ươ
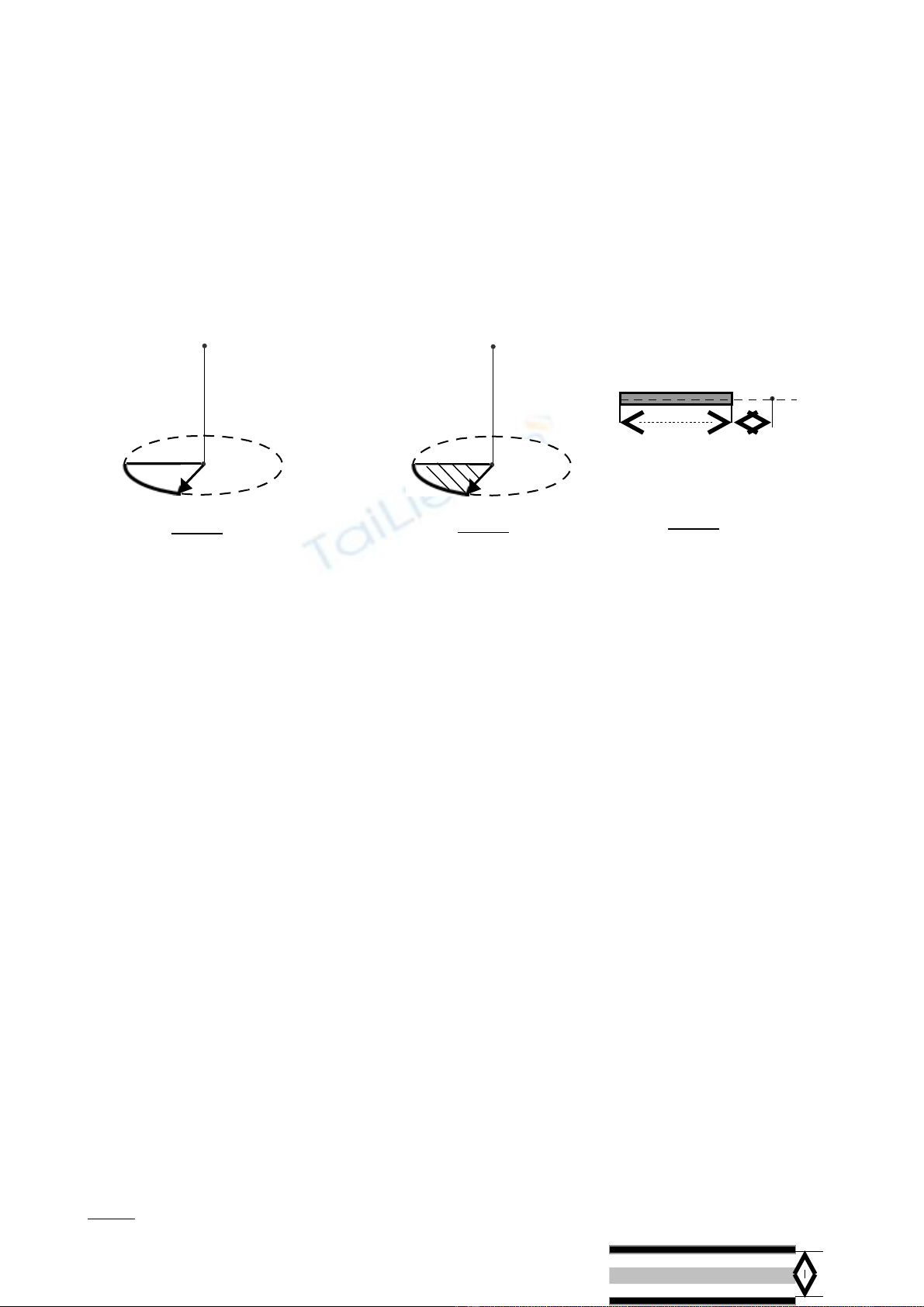
Bài 5: M t qu c u kh i l ng m, mang m t đi n tích q đ c bu c vào đ u cu i c a m tộ ả ầ ố ượ ộ ệ ượ ộ ầ ố ủ ộ
s i ch cách đi n. Đ u kia c a s i ch đ c bu c vào đi m cao nh t c a m t vòng dây cóợ ỉ ệ ầ ủ ợ ỉ ượ ộ ể ấ ủ ộ
bán kính R đ t trong m t m t ph ng th ng đ ng. Vòng dây đ c làm b ng m t dây d nặ ộ ặ ẳ ẳ ứ ượ ằ ộ ẫ
c ng có bán kính nh không đáng k . Vòng dây đ c tích m t đi n tích Q cùng d u v i đi nứ ỏ ể ượ ộ ệ ấ ớ ệ
tích q và phân b đ u đ n. Hãy xác đ nh chi u dài l c a s i dây treo đ sau khi b đ y l chố ề ặ ị ề ủ ợ ể ị ẩ ệ
qu c u s n m trên tr c gi a c a vòng dây vuông góc v i m t vòng dây.ả ầ ẽ ằ ụ ữ ủ ớ ặ
Đ u tiên hãy gi i bài toán d i d ng t ng quát, sau đó th c hi n các phép tính v i các sôầ ả ướ ạ ổ ự ệ ớ
li u Q = q = 9.10ệ-8C; R = 5cm; m = 1g; εo = 8,9.10-12F/m. B kh i l ng c a dây.ỏ ố ượ ủ
Bài 6: Hai m t ph ng r ng vô h n, đ t song song v i nhau, đ c tích đi n đ u trái d u v iặ ẳ ộ ạ ặ ớ ượ ệ ề ấ ớ
m t đ đi n m t ậ ộ ệ ặ σ và -σ. Xác đ nh c ng đ đi n tr ng t ng h p ị ườ ộ ệ ườ ổ ợ
E
r
do hai m t đó gây ra.ặ
Bài 7: Xác đ nh c ng đ đi n tr ng gây ra b i m t kh i c u bán kính R tích đi n đ u v iị ườ ộ ệ ườ ở ộ ố ầ ệ ề ớ
m t đ đi n kh i ậ ộ ệ ố ρ. V đ th bi u di n s ph thu c c a c ng đ đi n tr ng E vàoẽ ồ ị ể ễ ự ụ ộ ủ ườ ộ ệ ườ
kho ng cách r t đi m kh o sát đ n tâm O, E = E(r).ả ừ ể ả ế
Bài 8: Bên trong kh i c u cô l p tâm O bán kính R, tích đi n đ u v i m tố ầ ậ ệ ề ớ ậ
đ đi n kh i ộ ệ ố ρ có m t cái h c hình c u tâm Oộ ố ầ 1 bán kính r, v i OOớ1 = a
(Hv). Ch ng t r ng, bên trong h c đi n tr ng là đ u và có c ng đứ ỏ ằ ố ệ ườ ề ườ ộ
b ng . N u O1 trùng v i O thì k t qu s ra sao?ằ ế ớ ế ả ẽ
Bài 9: Đi n tr ng trong khí quy n có h ng th ng đ ng xu ng d i.ệ ườ ể ướ ẳ ứ ố ướ
C ng đ c a nó b ng 60V/m đ cao 300m và b ng 100V/m đ cao 200m.ườ ộ ủ ằ ở ộ ằ ở ộ
Tính l ng đi n tích ch a trong kh i không khí hình l p ph ng có c nh b ngượ ệ ứ ố ậ ươ ạ ằ
100m, n m gi a hai đ cao đó. Tính s ion (hóa tr 1) trung bình ch a trong 1mằ ữ ộ ố ị ứ 3
không khí. Nêu nh n xét v k t qu thu đ c.ậ ề ế ả ượ
Bài 10: M t bán c u kim lo i tâm O, bán kính R, mang đi n tích phân b đ uộ ầ ạ ệ ố ề
v i m t đ đi n m t ớ ậ ộ ệ ặ σ. Xác đ nh ph ng chi u c a cđđt t i đi m b t kì Mị ươ ề ủ ạ ể ấ
n m trong m t gi i h n bán c u, cách tâm O m t đo n r < R (hv).ằ ặ ớ ạ ầ ộ ạ
Bài 11: Kho ng không gian gi a hai m t ph ng song song có t a đ x = -a và x = a đ c tíchả ữ ặ ẳ ọ ộ ượ
đi n đ u v i m t đ đi n kh i ệ ề ớ ậ ộ ệ ố ρ (ρ>0). Xác đ nh c ng đ đi n tr ng t i m i đi m toànị ườ ộ ệ ườ ạ ọ ể
không gian. T đó tìm bi u th c c a đi n th t i m i đi m (ch n V = 0 t i x = a). V đ thừ ể ứ ủ ệ ế ạ ọ ể ọ ạ ẽ ồ ị
bi u di n s ph thu c c a E và V theo x. Xét tr ng h p x ể ễ ự ụ ộ ủ ườ ợ → ∞.
Bài 12: Trên m t vòng tròn bán kính R n m trong m t ph ng th ng đ ng có g n c đ nh haiộ ằ ặ ẳ ẳ ứ ắ ố ị
qu c u nh A, B mang đi n tích Q. hai qu c u nh khác là C và D có kh i l ng m vàả ầ ỏ ệ ả ầ ỏ ố ượ
đi n tích q, có th d ch chuy n không ma sát trên đ ng tròn. Bi t AB = R và có ph ngệ ể ị ể ườ ế ươ
n m ngang. Tìm đi u ki n đ khi cân b ng thì 4 qu c u n m trên 4 đ nh c a m t hìnhằ ề ệ ể ằ ả ầ ằ ỉ ủ ộ
vuông.
ĐI N TH , TH NĂNG TĨNH ĐI NỆ Ế Ế Ệ
1
O
M
r
R
σ
Tr ng THPT Chuyên L ng Văn Chánh – Phú yênườ ươ
Bài 1: M t thanh nh a đ c u n thành vòng tròn bán kính R có m t đi n tích d ng +Qộ ự ượ ố ộ ệ ươ
phân b đ u d theo m t ph n t chu vi c a nó và m t đi n tích âm -6Q phân b đ u trênố ề ọ ộ ầ ư ủ ộ ệ ố ề
ph n chu vi còn l i (hình v 1). V i V = 0 vô c c, h i đi n th :ầ ạ ẽ ớ ở ự ỏ ệ ế ở
a. Tâm O c a đ ng tròn?ủ ườ
b. Đi m P n m trên tr c qua tâm và vuông góc v i m t ph ng c a đ ng tròn và cáchể ằ ụ ớ ặ ẳ ủ ườ
tâm m t kho ng z?ộ ả
Bài 2: M t đĩa nh a đ c tích đi n m t phía v i m t đ đi n tích m t đ u ộ ự ượ ệ ộ ớ ậ ộ ệ ặ ề λ sau đó ¾
c a đĩa đ c c t b . Ph n còn l i đ c v nh hình 2. V i V = 0 vô c c, h i đi n thủ ượ ắ ỏ ầ ạ ượ ẽ ư ớ ở ự ỏ ệ ế
do ph n t còn l i gây ra đi m P, n m trên tr c qua tâm c a đĩa ban đ u và cách tâm banầ ư ạ ở ể ằ ụ ủ ầ
đ u m t kho ng z?ầ ộ ả
Bài 3: H i đi n th đi m P trên hình 3 cách đ u ph i c a m t thanh nh a có đ dài L vàỏ ệ ế ở ể ầ ả ủ ộ ự ọ
đi n tích toàn ph n –Q, m t kho ng d? Đi n tích đ c phân b đ u và V = 0 vô c c.ệ ầ ộ ả ệ ượ ố ề ở ự
Bài 4: M t b n m ng có d ng hình vành khăn bán kính trong a và bán kính ngoài b, tíchộ ả ỏ ạ
đi n q phân b đ u trên b n. Tìm đi n th t i đi m M n m trên tr c c a b n và cách tâmệ ố ề ả ệ ế ạ ể ằ ụ ủ ả
m t kho ng x.ộ ả
Bài 5: M t vòng dây tròn, bán kính R = 36cm, mang đi n tích Q = 7.10ộ ệ -7C, đ t trên m tặ ặ
ph ng n m ngang. Trên tr c vòng dây, t i đi m A, cách tâm O c a vòng dây m t đo n hẳ ằ ụ ạ ể ủ ộ ạ A
= 48cm, có đi n tích đi m Qệ ể o = 6.10-4C, đ c th cho Qượ ả o r i xu ng không v n t c đ u, khiơ ố ậ ố ầ
Qo đ n đi m B, cùng trên tr c c a vòng dây, hế ể ụ ủ B = 27cm, thì Qo b t đ u đi lên (hv). L y g =ắ ầ ấ
10m/s2.
a. Tính kh i l ng M c a đi n tích Qố ượ ủ ệ o.
b. Tính l c căng dây do Qựo gây ra cho vòng dây khi Qo đ n B.ế
Bài 6: Ba electron ban đ u đ ng yên ba đ nh c a tam giác đ u c nh a. Sau đó chúngầ ứ ở ỉ ủ ề ạ
chuy n đ ng do t ng tác tĩnh đi n. Tính v n t c c c đ i c a m i eletron đ t đ c.ể ộ ươ ệ ậ ố ự ạ ủ ỗ ạ ượ
Bài 7: M t qu bóng bay c a tr em đ c b m khí hêli, mang đi n tích q = - 5,5.10ộ ả ủ ẻ ượ ơ ệ -8C bay
th ng đ ng lên không khí m t kho ng d = 520m t v trí ban đ u A đ n v trí cu i B. Bìnhẳ ứ ộ ả ừ ị ầ ế ị ố
th ng đi n tr ng t n t i trong khí quy n g n m t đ t có c ng đ E = 150V/m vàườ ệ ườ ồ ạ ể ầ ặ ấ ườ ộ
h ng xu ng d i. Tính hi u th năng (đi n) c a qu bóng gi a các v trí A và B.ướ ố ướ ệ ế ệ ủ ả ữ ị
Bài 8: Có 3 đi n tích đi m qệ ể 1 = +q = +150nC, q2 = -4q và q3 = +2q đ c gi c đ nh t i baượ ữ ố ị ạ
đ nh c a m t tam giác đ u c nh a = 12cm. Xác đ nh th năng (đi n) c a h đi n tích đó.ỉ ủ ộ ề ạ ị ế ệ ủ ệ ệ
Bài 9: Hai qu c u nh tích đi n 1 và 2, có kh i l ng và đi n tích t ng ng là mả ầ ỏ ệ ố ượ ệ ươ ứ 1 = m,
q1 = +q; m2 =4m; q2 = +2q đ c đ t cách nhau m t đo n a. Ban đ u qu c u 2 đ ng yên vàượ ặ ộ ạ ầ ả ầ ứ
qu c u 1 chuy n đ ng h ng th ng vào qu c u 2 v i v n t c vả ầ ể ộ ướ ẳ ả ầ ớ ậ ố o.
a. Tính kho ng cách c c ti u rả ự ể min gi a hai qu c u.ữ ả ầ
b. Xét tr ng h p a = ườ ợ ∞, tính rmin.
c. Tính v n t c uậ ố 1, u2 c a hai qu c u khi chúng l i ra xa nhau vô cùng. B qua tácủ ả ầ ạ ỏ
d ng c a tr ng tr ng.ụ ủ ọ ườ
Bài 10: M t electron đ c b n v i v n t c ban đ u 3,2.10ộ ượ ắ ớ ậ ố ầ 5m/s h ng th ng đ n m tướ ẳ ế ọ
prôtôn đ c gi c đ nh t i ch . N u lúc đ u electron r t xa prôtôn thì kho ng cáchượ ữ ố ị ạ ỗ ế ầ ở ấ ở ả
nào đ i v i prôtôn, v n t c t c th i c a nó b ng hai v n t c ban đ u.ố ớ ậ ố ứ ờ ủ ằ ậ ố ầ
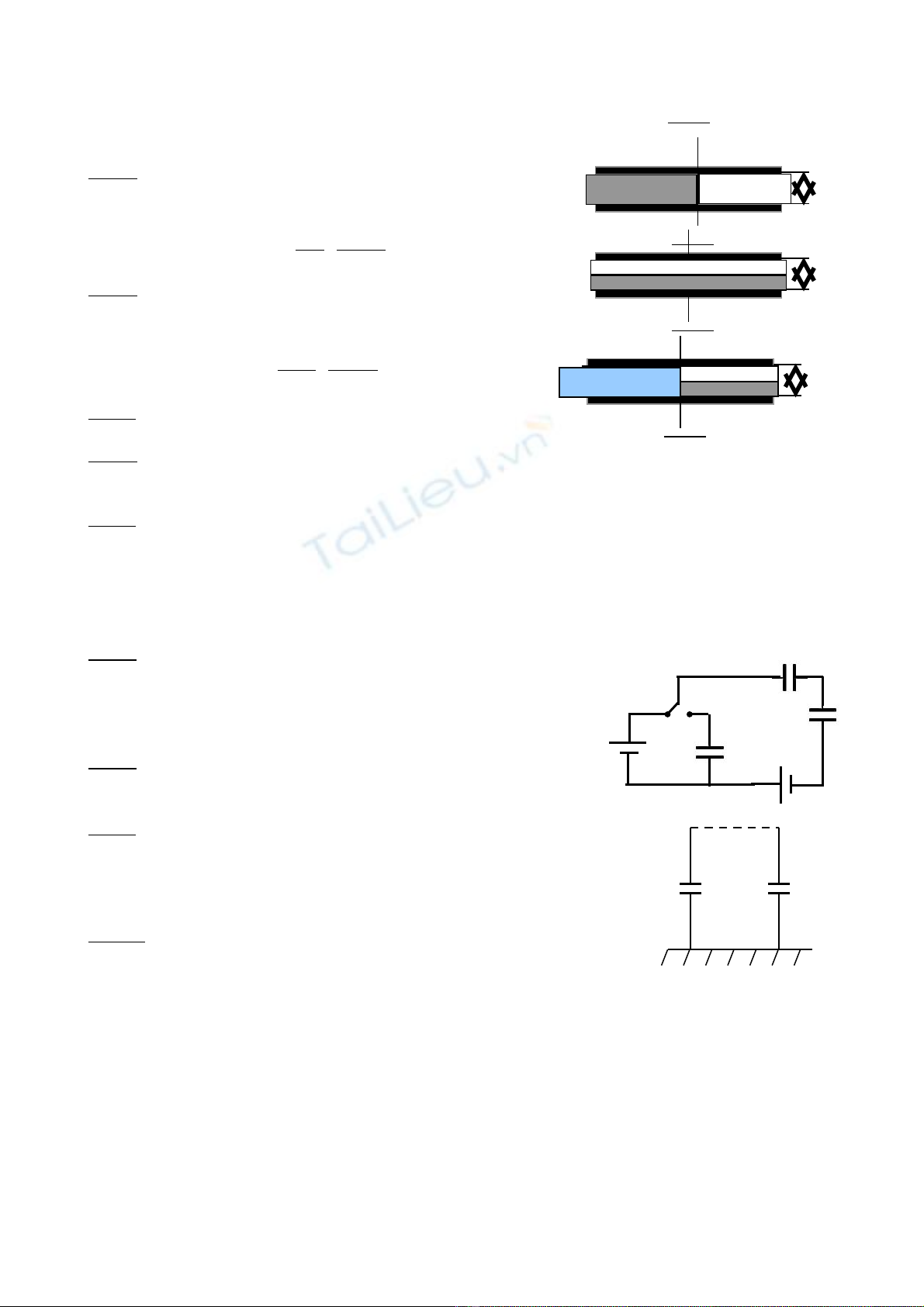
Bài 1: M t t m đ ng dày b đ c đ a vào m t t ph ng có di n tích b n S nh hình v 1. Chi uộ ấ ồ ượ ư ộ ụ ẳ ệ ả ư ẽ ề
dày t m đúng b ng n a kho ng cách gi a các b n. ấ ằ ử ả ữ ả
O
P
R
z
Hình 1
+Q
-6Q
O
P
R
z
Hình 2 Hình 3
P
Ld
2
d
Tr ng THPT Chuyên L ng Văn Chánh – Phú yênườ ươ
a. H i đi n dung sau khi đ a t m đ ng vào.ỏ ệ ư ấ ồ
b. N u có đi n tích Q đ c gi trên các b n thì t s c a năng l ng d tr tr c và năngế ệ ượ ữ ở ả ỉ ố ủ ượ ự ữ ướ
l ng d tr sau khi đ a tám đ ng vào b ng bao nhiêu? ượ ự ữ ư ồ ằ
c. H i công đ c th c hi n khi đ a t m đ ng vào? T mỏ ượ ự ệ ư ấ ồ ấ
b hút vào hay ph i đ y nó vào?ị ả ẩ
Bài 2: M t t ph ng có di n tích b n b ng S đ c l p đ yộ ụ ẳ ệ ả ằ ượ ắ ầ
b ng hai ch t đi n môi nh hình v 2. Ch ng minh r ng đi nằ ấ ệ ư ẽ ứ ằ ệ
dung đ c cho b i:ượ ở
1 2
2
oS
C
d
εε ε
+
=
Bài 3: M t t ph ng có di n tích b n b ng S đ c l p đ yộ ụ ẳ ệ ả ằ ượ ắ ầ
b ng hai ch t đi n môi nh hình v 3. Ch ng minh r ng đi nằ ấ ệ ư ẽ ứ ằ ệ
dung đ c cho b i:ượ ở
1 2
1 2
2oS
C
d
εε ε
ε ε
⋅
=
+
Bài 4: Tính đi n dung c a t có di n tích b n b ng S nhệ ủ ụ ệ ả ằ ư
hình v 4.ẽ
Bài 5: Tâm c a hai qu c u nh gióng nhau (bán kính r)ủ ả ầ ỏ
đ t cách nhau m t kho ng a trong chân không, chúng mang đi n tích l n l t là qặ ộ ả ệ ầ ượ 1 và q2. N u n iế ố
hai qu c u b ng m t dây d n thì th năng c a chúng tăng hay gi m m t l ng b ng bao nhiêu?ả ầ ằ ộ ẫ ế ủ ả ộ ượ ằ
Bài 6: Gi a hai b n c a t đi n ph ng là m t b n có đ dày b ng 1/3 kho ng cách hai b n, đ tữ ả ủ ụ ệ ẳ ộ ả ộ ằ ả ả ặ
song song v i hai b n. Đi n dung c a t khi ch a có b n là C = 0,025ớ ả ệ ủ ụ ư ả µF, t đ c n i v i ngu nụ ượ ố ớ ồ
nên nó đ c tích đi n đ n hi u đi n th U = 100V. Xác đ nh công Aượ ệ ế ệ ệ ế ị 1 c n tiêu t n đ kéo b nầ ố ể ả
ra? Công A2 do ngu n sinh ra khi đó?ồ
a. B n là t m đ ng.ả ấ ồ
b. B n là ch t đi n môi có ả ấ ệ ε = 3.
Bài 7: Cho m t t đi n có đi n dung Cộ ụ ệ ệ 1 = 0,5µF đ c tích đi nượ ệ
đ n hi u đi n th Uếệệế1 = 90V r i ng t kh i ngu n. M t t Cồ ắ ỏ ồ ộ ụ 2 khác
ch a tích đi n (Cư ệ 2 = 0,4µF) đ c ghép song song v i t trên. Khiượ ớ ụ
n i chúng phát ra m t tia l a đi n. Tính năng l ng c a tia l aố ộ ử ệ ượ ủ ử
đi n này.ệ
Bài 8: Trong m ch đi n nh hình v , khóa K đ c đóng v tríạ ệ ư ẽ ượ ở ị
1. Ta chuy n khóa K sang v trí 2. Hãy tính đi n tích Qể ị ệ 1, Q2, Q3 và
hi u đi n th Uệ ệ ế 1, U2, U3 trên các t đi n.ụ ệ
Bài 9: Hai t đi n Cụ ệ 1 = 2µF, C2 = 0,5µF có m t b n n i đ t, hi u đi nộ ả ố ấ ệ ệ
th gi a các b n phía trên c a các t đi n và các b n n i đ t l n l tế ữ ả ủ ụ ệ ả ố ấ ầ ượ
b ng Uằ1 = 200V, U2 = -100V (hình v ). Tính nhi t l ng t a ra khi n iẽ ệ ượ ỏ ố
các b n phía trên (b n không n i đ t) c a hai t đi n b ng m t dâyả ả ố ấ ủ ụ ệ ằ ộ
d n.ẫ
Bài 10: Hai b n c a m t t đi n ph ng đ t th ng đ ng có chi u r ngả ủ ộ ụ ệ ẳ ặ ẳ ứ ề ộ
b, chi u cao h, đ t cách nhau m t kho ng r t nh d (d << b, h). Mépề ặ ộ ả ấ ỏ
d i c u hai b n t đi n ch m vào m t kh i đi n môi l ng có h ng sướ ả ả ụ ệ ạ ộ ố ệ ỏ ằ ố
đi n môi là ệε và khói l ng riêng D.ượ
a. N i hai b n t đi n v i ngu n đi n có hi u đi n th U, ng i ta th y đi n môi dâng lênố ả ụ ệ ớ ồ ệ ệ ệ ế ườ ấ ệ
trong kho ng gi a hai b n đ n đ cao H. Hãy gi i thích hi n t ng đó và tính H. B quaả ữ ả ế ộ ả ệ ượ ỏ
hi n t ng mao d n.ệ ượ ẫ
b. N u tr c khi cho hai b n t đi n ch m vào m t ch t l ng, ng i ta tích đi n r i ng tế ướ ả ụ ệ ạ ặ ấ ỏ ườ ệ ồ ắ
t đi n kh i ngu n hi n t ng không có gì khác tr c. Tính đ cao c t đi n môi gi a haiụ ệ ỏ ồ ệ ượ ướ ộ ộ ệ ữ
b n.ả
3
Hình 1
Hình 2
d
ε1
ε2
Hình 3
d
ε1
ε2
Hình 4
d
ε3
ε2
ε1
K
12
C1
C3
C1
E1E2
MN
U1U2
C1C2
Tr ng THPT Chuyên L ng Văn Chánh – Phú yênườ ươ
Bài 1: Hai b n c a m t t đi n ph ng là hai t m kim lo i di n tích S, đ t cách nhau m t kho ng d,ả ủ ộ ụ ệ ẳ ấ ạ ệ ặ ộ ả
mang đi n tích +q và –q. Kho ng không gian gi a hai b n là m t kh i đi n môi có h ng s đi n môiệ ả ữ ả ộ ố ệ ằ ố ệ
ph thu c vào t a đ x theo hàm s ụ ộ ọ ộ ố ε = ε(x) (tr c x vuông góc v i các b n); sát b n d ng, h ng sụ ớ ả ở ả ươ ằ ố
đi n môi có tr s ệ ị ố ε1, còn sát b n âm nó có tr s ở ả ị ố ε2 >ε1.
a. Tìm l ng đi n tích phân c c t ng c ng bên trong kh i đi n môi.ượ ệ ự ổ ộ ố ệ
b. Cho bi t ếε(x) là hàm b c nh t c a x, hãy tìm hi u đi n th đ t vào t đi n và đi n dung c aậ ấ ủ ệ ệ ế ặ ụ ệ ệ ủ
t đi n đó.ụ ệ
c. Áp d ng s : q = 3,2.10-9C, ụ ố ε1 = 4, ε2 = 10, d = 1,8cm, S = 100cm2.
Bài 2: M t v t d n A hình c u bán kính Rộ ậ ẫ ầ 1 = 3cm, tích đi n đ n đi n th Vệ ế ệ ế 1 = 4V, đ c đ t đ ng tâmượ ặ ồ
v i m t qu c u m ng B b ng kim lo i có bán kính trong Rớ ộ ả ầ ỏ ằ ạ 2 = 12cm và bán kính ngoài R3 = 12,1cm, vỏ
c u này g m hai bán c u ban đ u đ c úp khít vào nhau và sau đó đ c tích đi n đ n đi n th Vầ ồ ầ ầ ượ ượ ệ ế ệ ế 2.
H i đi n th Vỏ ệ ế 2 ph i có tr s (d ng) t i thi u b ng bao nhiêu đ hai bán c u có th t tách kh iả ị ố ươ ố ể ằ ể ầ ể ự ỏ
nhau.
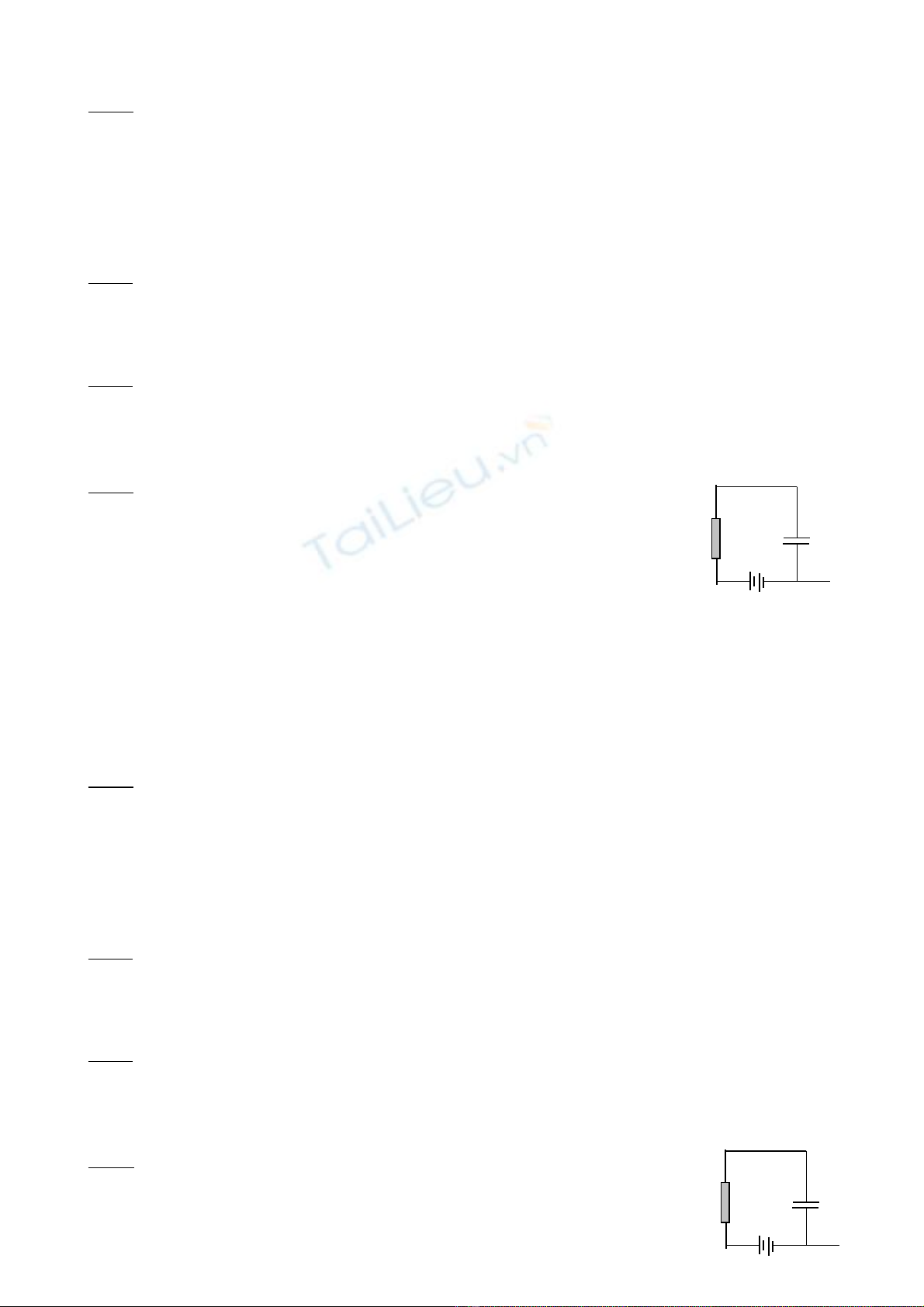
Bài 3: Hai t ph ng gi ng nhaucó di n tích b ng S = 400cmụ ẳ ố ệ ằ 2 và kho ng cách các b n dả ả 1 = 0,6mm đ cượ
n i v i nhau (hv) b ng hai đi n tr R = 12,5kố ớ ằ ệ ở Ω. Các b n đ c đ a ra cách nhau dả ượ ư 2 = 1,8mm trong th iờ
gain t = 3s, l n đ u đ ng th i tách xa các b n c a c hai t , l n sau l n l t t này r i đ n t kia. ầ ầ ồ ờ ả ủ ả ụ ầ ầ ượ ụ ồ ế ụ
Bi t hi u đi n th gi a các b n c a hai t lúc đ u U = 500V, h i tr ng h p nào t n công nhi uế ệ ệ ế ữ ả ủ ụ ầ ỏ ườ ợ ố ề
h n, và t n h n bao nhiêu?ơ ố ơ
Bài 4: M t t đi n ph ng không khí (h ng s đi n môi ộ ụ ệ ẳ ằ ố ệ ε = 1), di n tích m i b nệ ỗ ả
c c là S = 2cmự2, kho ng cách các b n là d = 0,002cm. M t b n c c đ c n i đ t,ả ả ộ ả ự ượ ố ấ
b n c c kia n i v i đi n tr R = 10Mả ự ố ớ ệ ở Ω r i vào c c d ng c a m t pin có E = 90Vồ ự ươ ủ ộ
(hv).
a. Sau m t kho ng th i gian đ dài, ta tách b n c c trên c a t đi n kh i đi nộ ả ờ ủ ả ự ủ ụ ệ ỏ ệ
tr và cho nó dao đ ng sao cho kho ng cách gi a hai b n c c c a t đi n bi nở ộ ả ữ ả ự ủ ụ ệ ế
thiên đi u hòa (hình sin) v i t n s f = 1000Hz, biên đ a = 0,00002cm. Ch ng minh r ng đi n th b nề ớ ầ ố ộ ứ ằ ệ ế ả
c c trên có th vi t g n đúng b ng t ng c a m t đi n th không đ i V và m t đi n th tu n hoànự ể ế ầ ằ ổ ủ ộ ệ ế ổ ộ ệ ế ầ
v.sin(ωt). Hãy xác đ nh V, v, ịω.
b. Gi s các b n c c c a t đi n v n đ c n i nh hình v , và kho ng cách gi a hai b n bi nả ử ả ự ủ ụ ệ ẫ ượ ố ư ẽ ả ữ ả ế
thiên nh trong câu a. Dòng đi n trong m ch có d ng i = iư ệ ạ ạ osin(ωt + ϕ). Hãy tính giá tr iịo và ϕ.
Bài 1: Hai b n c a m t t đi n ph ng là hai t m kim lo i di n tích S, đ t cách nhau m t kho ng d,ả ủ ộ ụ ệ ẳ ấ ạ ệ ặ ộ ả
mang đi n tích +q và –q. Kho ng không gian gi a hai b n là m t kh i đi n môi có h ng s đi n môiệ ả ữ ả ộ ố ệ ằ ố ệ
ph thu c vào t a đ x theo hàm s ụ ộ ọ ộ ố ε = ε(x) (tr c x vuông góc v i các b n); sát b n d ng, h ng sụ ớ ả ở ả ươ ằ ố
đi n môi có tr s ệ ị ố ε1, còn sát b n âm nó có tr s ở ả ị ố ε2 >ε1.
a. Tìm l ng đi n tích phân c c t ng c ng bên trong kh i đi n môi.ượ ệ ự ổ ộ ố ệ
b. Cho bi t ếε(x) là hàm b c nh t c a x, hãy tìm hi u đi n th đ t vào t đi n và đi n dung c aậ ấ ủ ệ ệ ế ặ ụ ệ ệ ủ
t đi n đó.ụ ệ
c. Áp d ng s : q = 3,2.10-9C, ụ ố ε1 = 4, ε2 = 10, d = 1,8cm, S = 100cm2.
Bài 2: M t v t d n A hình c u bán kính Rộ ậ ẫ ầ 1 = 3cm, tích đi n đ n đi n th Vệ ế ệ ế 1 = 4V, đ c đ t đ ng tâmượ ặ ồ
v i m t qu c u m ng B b ng kim lo i có bán kính trong Rớ ộ ả ầ ỏ ằ ạ 2 = 12cm và bán kính ngoài R3 = 12,1cm, vỏ
c u này g m hai bán c u ban đ u đ c úp khít vào nhau và sau đó đ c tích đi n đ n đi n th Vầ ồ ầ ầ ượ ượ ệ ế ệ ế 2.
H i đi n th Vỏ ệ ế 2 ph i có tr s (d ng) t i thi u b ng bao nhiêu đ hai bán c u có th t tách kh iả ị ố ươ ố ể ằ ể ầ ể ự ỏ
nhau.
Bài 3: Hai t ph ng gi ng nhaucó di n tích b ng S = 400cmụ ẳ ố ệ ằ 2 và kho ng cách các b n dả ả 1 = 0,6mm đ cượ
n i v i nhau (hv) b ng hai đi n tr R = 12,5kố ớ ằ ệ ở Ω. Các b n đ c đ a ra cách nhau dả ượ ư 2 = 1,8mm trong th iờ
gain t = 3s, l n đ u đ ng th i tách xa các b n c a c hai t , l n sau l n l t t này r i đ n t kia. ầ ầ ồ ờ ả ủ ả ụ ầ ầ ượ ụ ồ ế ụ
Bi t hi u đi n th gi a các b n c a hai t lúc đ u U = 500V, h i tr ng h p nào t n công nhi uế ệ ệ ế ữ ả ủ ụ ầ ỏ ườ ợ ố ề
h n, và t n h n bao nhiêu?ơ ố ơ
Bài 4: M t t đi n ph ng không khí (h ng s đi n môi ộ ụ ệ ẳ ằ ố ệ ε = 1), di n tích m i b nệ ỗ ả
c c là S = 2cmự2, kho ng cách các b n là d = 0,002cm. M t b n c c đ c n i đ t,ả ả ộ ả ự ượ ố ấ
b n c c kia n i v i đi n tr R = 10Mả ự ố ớ ệ ở Ω r i vào c c d ng c a m t pin có E = 90Vồ ự ươ ủ ộ
(hv).
4

Tr ng THPT Chuyên L ng Văn Chánh – Phú yênườ ươ
a. Sau m t kho ng th i gian đ dài, ta tách b n c c trên c a t đi n kh i đi n tr và cho nó daoộ ả ờ ủ ả ự ủ ụ ệ ỏ ệ ở
đ ng sao cho kho ng cách gi a hai b n c c c a t đi n bi n thiên đi u hòa (hình sin) v i t nộ ả ữ ả ự ủ ụ ệ ế ề ớ ầ
s f = 1000Hz, biên đ a = 0,00002cm. Ch ng minh r ng đi n th b n c c trên có th vi t g nố ộ ứ ằ ệ ế ả ự ể ế ầ
đúng b ng t ng c a m t đi n th không đ i V và m t đi n th tu n hoàn v.sin(ằ ổ ủ ộ ệ ế ổ ộ ệ ế ầ ωt). Hãy xác
đ nh V, v, ịω.
b. Gi s các b n c c c a t đi n v n đ c n i nh hình v , và kho ng cách gi a hai b n bi nả ử ả ự ủ ụ ệ ẫ ượ ố ư ẽ ả ữ ả ế
thiên nh trong câu a. Dòng đi n trong m ch có d ng i = iư ệ ạ ạ osin(ωt + ϕ). Hãy tính giá tr iịo và ϕ.
5


























