21
F
F
12
F
q1.q2 >0
r
21
F
12
F
r
q1.q2 < 0
TÓM T T CÔNG TH C VÀ LÍ THUY T MÔN V T LÝ 11Ắ Ứ Ế Ậ
CH NG I.ƯƠ ĐI N TÍCH – ĐI N TR NGỆ Ệ ƯỜ
I. Cách nhi m đi nễ ệ . Có 3 cách nhi m đi n m t v t: C xát, ti p xúc ,h ng ngễ ệ ộ ậ ọ ế ưở ứ
II. Đnh lu t Cu lôngị ậ :
L c t ng tác gi a 2 đi n tích đi m qự ươ ữ ệ ể 1; q2 đt cách nhau m t kho ng r trong môi tr ng cóặ ộ ả ườ
h ng s đi n môi là εằ ố ệ
12 21
;F F
có:
- Đi m đt: trên 2 đi n tích.ể ặ ệ
- Ph ng: đng n i 2 đi n tích.ươ ườ ố ệ
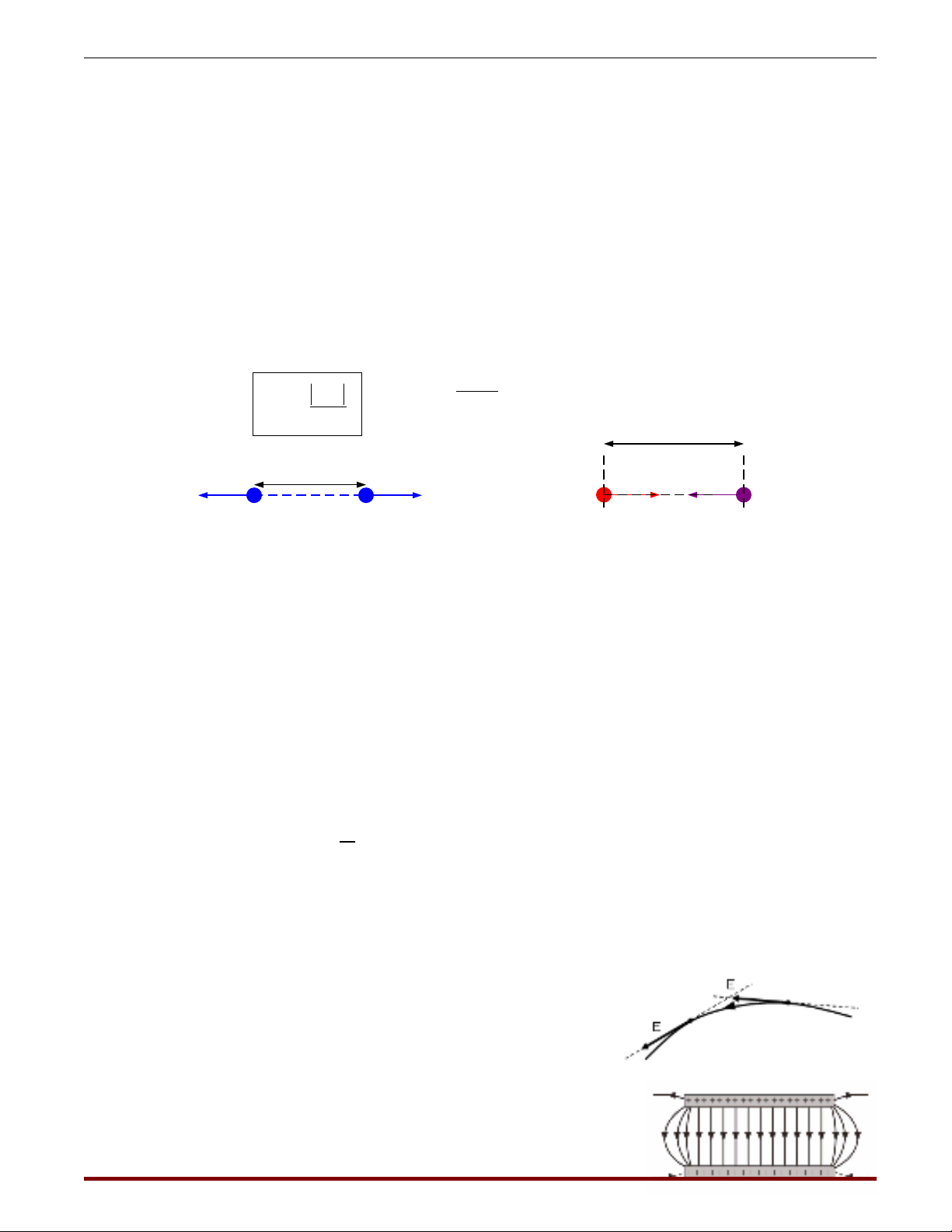
- Chi u: ề+ H ng ra xa nhau n u ướ ế q1.q2 > 0 (q1; q2 cùng d u)ấ
+ H ng vào nhau n u ướ ế q1.q2 < 0 (q1; q2 trái d u)ấ
- Đ l n: ộ ớ
2
21
.r
qq
kF
; k = 9.109
2
2
.N m
C
� �
� �
� �
(ghi chú: F là l c tĩnh đi n)ự ệ
- Bi u di n:ể ễ
3. V t d n đi n, đi n môiậ ẫ ệ ệ :
+ V t (ch t) có nhi u đi n tích t do ậ ấ ề ệ ự d n đi nẫ ệ
+ V t (ch t) có ch a ít đi n tích t do ậ ấ ứ ệ ự cách đi n. (đi n môi)ệ ệ
4. Đnh lu t b o toàn đi n tích:ị ậ ả ệ Trong 1 h cô l p v đi n (h không trao đi đi n tích v i cácệ ậ ề ệ ệ ổ ệ ớ
h khác) thì t ng đi s các đi n tích trong h là 1 h ng sệ ổ ạ ố ệ ệ ằ ố
III. Đi n tr ngệ ườ
+ Khái ni m:ệ Là môi tr ng t n t i xung quanh đi n tích và tác d ng l c lên đi n tíchườ ồ ạ ệ ụ ự ệ
khác đt trong nó. ặ
+ C ng đ đi n tr ngườ ộ ệ ườ : Là đi l ng đc tr ng cho đi n tr ng v kh năng tác d ngạ ượ ặ ư ệ ườ ề ả ụ
l c.ự
EqF
q
F
E
.
Đn v : E(V/m)ơ ị
q > 0 :
F
cùng ph ng, cùng chi u v i ươ ề ớ
E
.
q < 0 :
F
cùng ph ng, ng c chi u v iươ ượ ề ớ
E
.
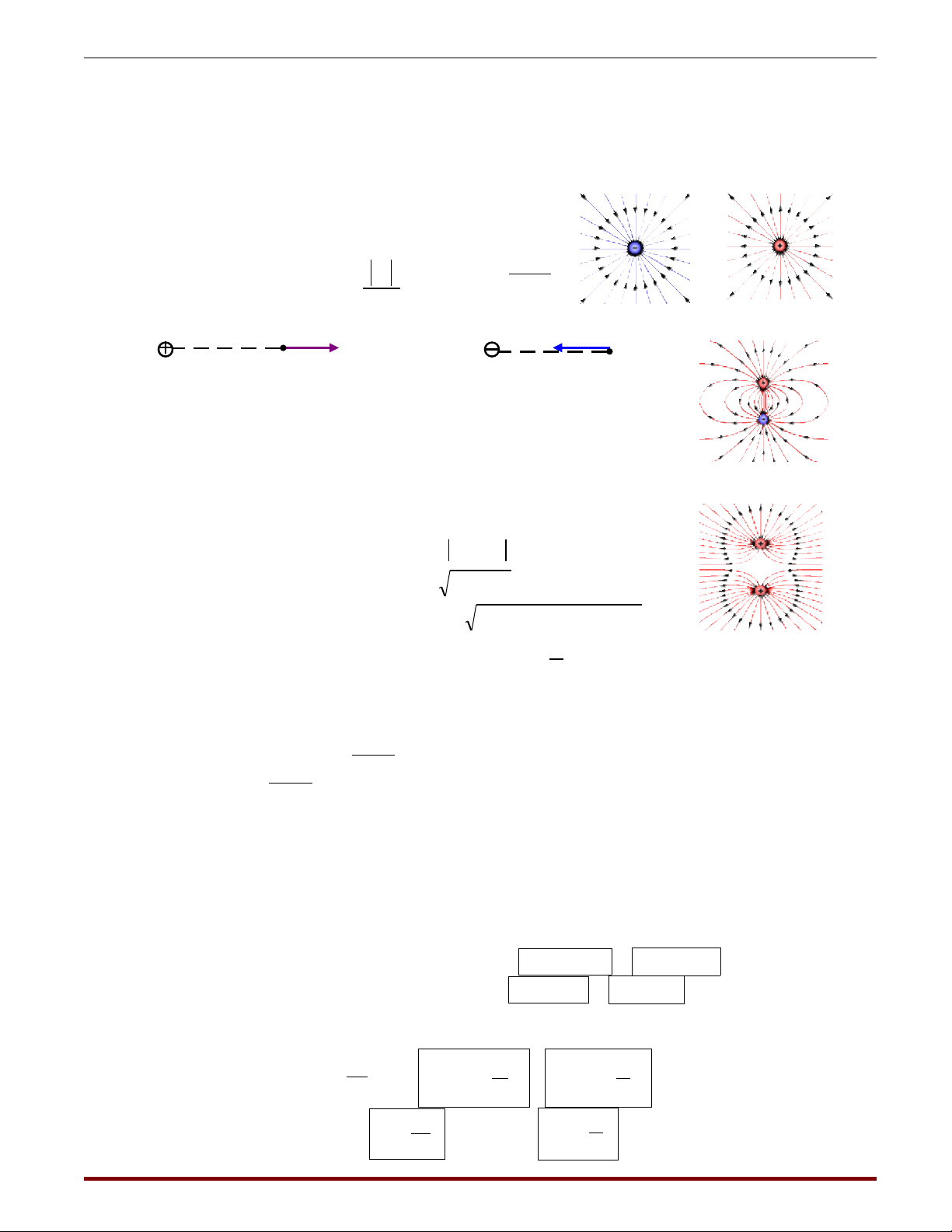
+ Đng s c đi n tr ngườ ứ ệ ườ : Là đng đc v trong đi n tr ng sao cho h ng c a ti pườ ượ ẽ ệ ườ ướ ủ ế
t y n t i b t k đi m nào trên đng cũng trùng v i h ng c a véc t CĐĐT t i đi m đó.ư ế ạ ấ ỳ ể ườ ớ ướ ủ ơ ạ ể
Tính ch t c a đng s c:ấ ủ ườ ứ
- Qua m i đi m trong đ.tr ng ta ch có th vỗ ể ườ ỉ ể ẽ
đc 1 và ch 1 đng s c đi n tr ng.ượ ỉ ườ ứ ệ ườ
- Các đng s c đi n là các đng cong khôngườ ứ ệ ườ
kín,nó xu t phát t các đi n tích d ng,t n cùng cácấ ừ ệ ươ ậ ở
đi n tích âm. ệ
- Các đng s c đi n không bao gi c t nhau. ườ ứ ệ ờ ắ
- N i nào có CĐĐT l n h n thì các đng s c đóơ ớ ơ ườ ứ ở
v mau và ng c l iẽ ượ ạ
Trang 1
rr
+ Đi n tr ng đuệ ườ ề :
- Có véc t CĐĐT t i m i đi m đu b ng nhau. ơ ạ ọ ể ề ằ
- Các đng s c c a đi n tr ng đu là các đng th ng song song cách đu nhauườ ứ ủ ệ ườ ề ườ ẳ ề
+ Véct c ng đ đi n tr ng ơ ườ ộ ệ ườ
E
do 1 đi n tích đi m Q gây ra t i m t đi m Mệ ể ạ ộ ể cách Q
m t đo n r có: - Đi m đt: T i M.ộ ạ ể ặ ạ
- Ph ng: ươ đng n i M và Qườ ố
- Chi u: ềH ng ra xa Q n u Q > 0ướ ế
H ng vào Q n u Q <0ướ ế
- Đ l n:ộ ớ
2
.
Q
E k r
ε
=
; k = 9.109
2
2
.N m
C
� �
� �
� �
- Bi u di n:ể ễ
+ Nguyên lí ch ng ch t đi n tr ngồ ấ ệ ườ :
1 2
.....
n
E E E E
= + + +
Xét tr ng h p t i đi m đang xét ch có 2 c ng đ đi n tr ng ườ ợ ạ ể ỉ ườ ộ ệ ườ
+
21 EEE
+
2121 EEEEE
+
2121 EEEEE
+
2
2
2
121 EEEEE
+
cos2, 21
2
2
2
121 EEEEEEE
N u ế
2
cos2 121
EEEE
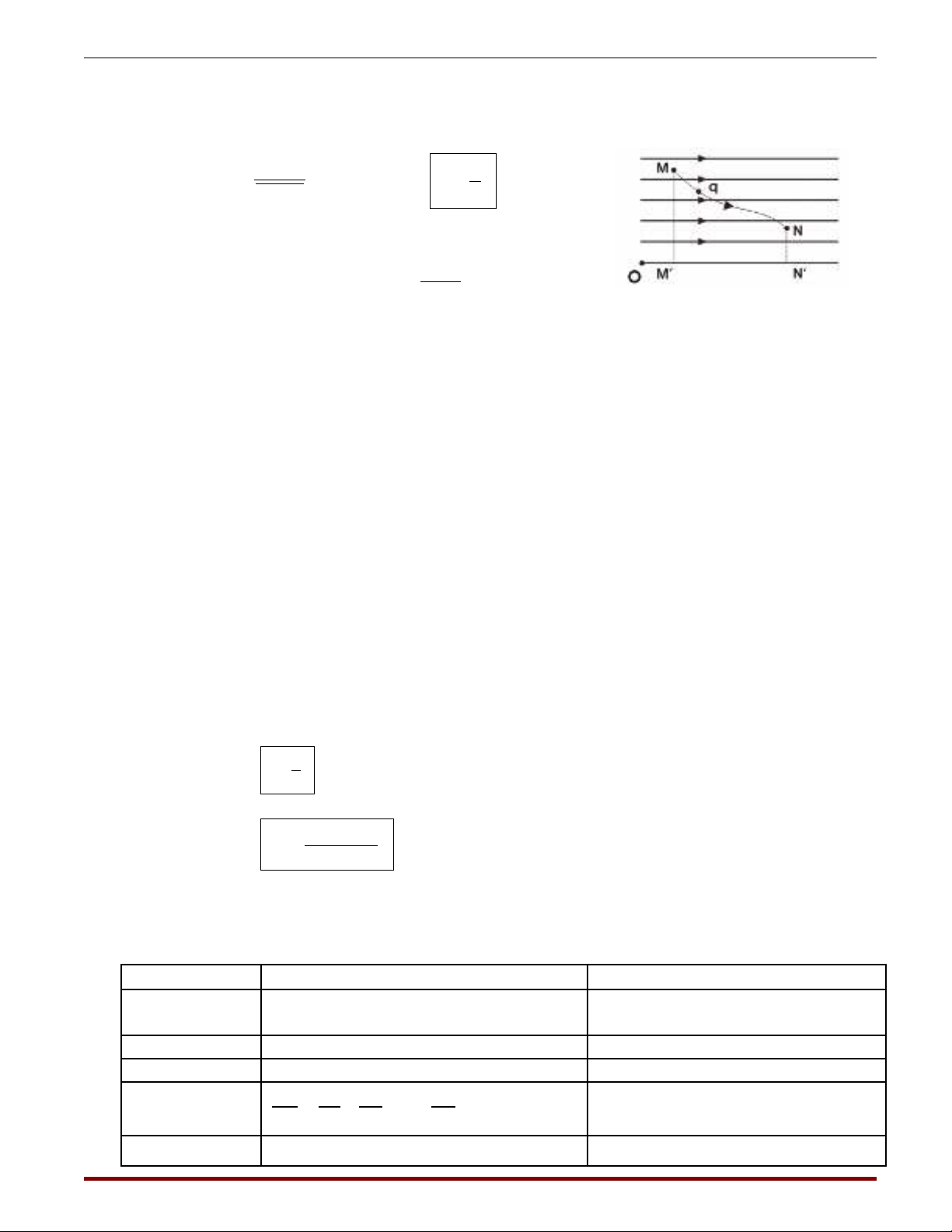
IV. Công c a l c đi n tr ng:ủ ự ệ ườ Công c a l c đi n tác d ng vào 1 đi n tích không ph thu c vàoủ ự ệ ụ ệ ụ ộ
d ng c a đng đi c a đi n tích mà ch ph thu c vào v trí đi m đu,đi m cu i c a đng đi trongạ ủ ườ ủ ệ ỉ ụ ộ ị ể ầ ể ố ủ ườ
đi n tr ngệ ườ
AMN = q.E.
'' NM
= q.E.dMN
(v i dớ
MN
=
''
NM
là đ dài đi s c a hình chi u c a đng đi MN lên tr c to đ ox v iộ ạ ố ủ ế ủ ườ ụ ạ ộ ớ
chi u d ng c a tr c ox là chi u c a đng s c)ề ươ ủ ụ ề ủ ườ ứ
. Liên h gi a công c a l c đi n và hi u th năng c a đi n tíchệ ữ ủ ự ệ ệ ế ủ ệ
AMN = WM - WN = q VM - q.VN =q(VM-VN)=q.UMN
. Th năng đi n tr ng-ế ệ ườ Đi n th t i các đi m M,Nệ ế ạ ể
+ Đi v i đi n tr ng đu gi a hai b n t :ố ớ ệ ườ ề ữ ả ụ
MM
qEdW
;
NN
qEdW
(J)
MM
EdV
;
NN
EdV
(V)
dM, dN là kho ng cách t đi m M,N đn b n âm c a t .ả ừ ể ế ả ủ ụ
+ Đi v i điên tr ng c a m t đi n tích : ố ớ ườ ủ ộ ệ
M
M
MM d
r
Q
qkqEdW
M
M
r
Q
kqW
;
N
N
r
Q
kqW
Đi n th : ệ ế
q
W
V
M
M
suy ra:
M
M
r
Q
kV
Trang 2
M
E
q > 0 q < 0
M
E
dM=rM, dN=rN là kho ng cách t Q đn M,Nả ừ ế
+ Hi u đi n th gi a 2 đi m trong đi n tr ng là đi l ng đc tr ng cho kh năng th cệ ệ ế ữ ể ệ ườ ạ ượ ặ ư ả ự
hi n công c a đi n tr ng khi có 1 đi n tích di chuy n gi a 2 đi m đóệ ủ ệ ườ ệ ể ữ ể
. Liên h gi a E và Uệ ữ
''
NM
U
E
MN
hay :
d
U
E
* Ghi chú: công th c chung cho 3 ph n 6, 7, 8:ứ ầ
.
MN
MN M N MN
A
U V V E d
q
= − = =
V. V t d n trong đi n tr ngậ ẫ ệ ườ
- Khi v t d n đt trong đi n tr ng mà không có dòng đi n ch y trong v t thì ta g i là v tậ ẫ ặ ệ ườ ệ ạ ậ ọ ậ
d n cân b ng đi n (vdcbđ)ẫ ằ ệ
+ Bên trong vdcbđ c ng đ đi n tr ng b ng không.ườ ộ ệ ườ ằ
+ M t ngoài vdcbđ: c ng đ đi n tr ng có ph ng vuông góc v i m t ngoàiặ ườ ộ ệ ườ ươ ớ ặ
+ Đi n th t i m i đi m trên vdcbđ b ng nhauệ ế ạ ọ ể ằ
+ Đi n tích ch phân b m t ngoài c a v t, s phân b là không đu (t p trung ch l iệ ỉ ố ở ặ ủ ậ ự ố ề ậ ở ỗ ồ
nh n)ọ
VI. Đi n môi trong đi n tr ngệ ệ ườ
- Khi đt m t kh i đi n môi trong đi n tr ng thì nguyên t c a ch t đi n môi đc kéoặ ộ ố ệ ệ ườ ử ủ ấ ệ ượ
dãn ra m t chút và chia làm 2 đu mang đi n tích trái d u ộ ầ ệ ấ (đi n môi b phân c c).ệ ị ự K t qu làế ả
trong kh i đi n môi hình thành nên m t đi n tr ng ph ng c chi u v i đi n tr ng ngoàiố ệ ộ ệ ườ ụ ượ ề ớ ệ ườ
VII. T đi nụ ệ
- Đnh nghĩaị: H 2 v t d n đt g n nhau, m i v t là 1 b n t . Kho ng không gian gi a 2ệ ậ ẫ ặ ầ ỗ ậ ả ụ ả ữ
b n là chân không hay đi n môi ả ệ
T đi n ph ng ụ ệ ẳ có 2 b n t là 2 t m kim lo i ph ng có kích th c l n ,đt đi di n nhau,ả ụ ấ ạ ẳ ướ ớ ặ ố ệ
song song v i nhauớ
- Đi n dung c a t :ệ ủ ụ Là đi l ng đc tr ng cho kh năng tích đi n c a t ạ ượ ặ ư ả ệ ủ ụ
Q
CU
=
(Đn v là F.)ơ ị
Công th c tính đi n dung c a t đi n ph ngứ ệ ủ ụ ệ ẳ :
d
S
C.4.10.9
.
9
. V i S là ph n di n tích đi di n gi a 2 b n.ớ ầ ệ ố ệ ữ ả
Ghi chú : V i m i m t t đi n có 1 hi u đi n th gi i h n nh t đnh, n u khi s d ng màớ ỗ ộ ụ ệ ệ ệ ế ớ ạ ấ ị ế ử ụ
đt vào 2 b n t hđt l n h n hđt gi i h n thì đi n môi gi a 2 b n b đánh th ng.ặ ả ụ ớ ơ ớ ạ ệ ữ ả ị ủ
- Ghép t đi n song song, n i ti pụ ệ ố ế
GHÉP N I TI PỐ Ế GHÉP SONG SONG
Cách m cắ : B n th hai c a t 1 n i v i b n thả ứ ủ ụ ố ớ ả ứ
nh t c a t 2, c th ti p t c ấ ủ ụ ứ ế ế ụ B n th nh t c a t 1 n i v i b nả ứ ấ ủ ụ ố ớ ả
th nh t c a t 2, 3, 4 … ứ ấ ủ ụ
Đi n tíchệQB = Q1 = Q2 = … = QnQB = Q1 + Q2 + … + Qn
Hi u đi n thệệế UB = U1 + U2 + … + UnUB = U1 = U2 = … = Un
Đi n dungệ
n21B
C
1
...
C
1
C
1
C
1
CB = C1 + C2 + … + Cn
Ghi chúCB < C1, C2 … CnCB > C1, C2, C3
Trang 3
- Năng l ng c a t đi nượ ủ ụ ệ :
2 2
. .
2 2 2
QU C U Q
WC
= = =
- Năng l ng đi n tr ngượ ệ ườ : Năng l ng c a t đi n chính là năng l ng c a đi n tr ngượ ủ ụ ệ ượ ủ ệ ườ
trong t đi n. ụ ệ
T đi n ph ngụ ệ ẳ
2
9
. .
9.10 .8.
E V
W
ε
π
=
v i V=S.d là th tích kho ng không gian gi a 2 b n t đi n ph ngớ ể ả ữ ả ụ ệ ẳ
M t đ năng l ng đi n tr ng:ậ ộ ượ ệ ườ
2
8
W E
wV k
ε
π
= =
CH NG II.ƯƠ DÒNG ĐI N KHÔNG ĐIỆ Ổ
I. DÒNG ĐI NỆ
Dòng đi n là dòng các đi n tích (các h t t i đi n) di chuy n có h ng ệ ệ ạ ả ệ ể ướ
Chi u quy c c a dòng đi n là chi u d ch chuy n có h ng c a các đi n tích d ng.ề ướ ủ ệ ề ị ể ướ ủ ệ ươ
Dòng đi n có:ệ
* tác d ng t (đc tr ng) ụ ừ ặ ư (Chi u quy c I)ế ướ
* tác d ng nhi t, tác d ng hoá h c tu theo môi tr ng.ụ ệ ụ ọ ỳ ườ
C ng đ dòng đi n là đi l ng cho bi t đ m nh c a dòng đi n đc tính b i:ườ ộ ệ ạ ượ ế ộ ạ ủ ệ ượ ở
q: đi n l ng di chuy n qua các ti t di n th ng c a v t d nệ ượ ể ế ệ ẳ ủ ậ ẫ
t: th i gian di chuy nờ ể
(t0: I là c ng đ t c th i)ườ ộ ứ ờ
Dòng đi n có chi u và c ng đ không thay đi theo th i gian đc g i là dòng đi n khôngệ ề ườ ộ ổ ờ ượ ọ ệ
đi (cũng g i là dòng đi p m t chi u).ổ ọ ệ ộ ề
C ng đ c a dòng đi n này có th tính b i:ườ ộ ủ ệ ể ở
q
I = t
trong đó q là đi n l ng d ch chuy n qua ti t di n th ng c a v t d n trong th i gian t.ệ ượ ị ể ế ệ ẳ ủ ậ ẫ ờ
Ghi chú:
a) C ng đ dòng đi n không đi đc đo b ng ampe k (hay miliampe k , ườ ộ ệ ổ ượ ằ ế ế . . . ) m c xen vàoắ
m ch đi n (m c n i ti p). ạ ệ ắ ố ế
b) V i b n ch t dòng đi n và đnh nghĩa c a c ng đ dòng đi n nh trên ta suy ra:ớ ả ấ ệ ị ủ ườ ộ ệ ư
* c ng đ dòng đi n có giá tr nh nhau t i m i đi m trên m ch không phân nhánh.ườ ộ ệ ị ư ạ ọ ể ạ
* c ng đ m ch chính b ng t ng c ng đ các m ch r .ườ ộ ạ ằ ổ ườ ộ ạ ẽ
II. ĐNH LU T ÔM ĐI V I ĐO N M CH CH CÓ ĐIÊN TRỊ Ậ Ố Ơ Ạ Ạ Ỉ Ở
1) Đnh lu t: ị ậ
C ng đ dòng đi n ch y qua đo n m ch có có đi n tr R:ườ ộ ệ ạ ạ ạ ệ ở
- t l thu n v i hi u đi n th hai đu đo n m ch.ỉ ệ ậ ớ ệ ệ ế ầ ạ ạ
- t l ngh ch v i đi n tr . ỉ ệ ị ớ ệ ở
R
U
I
(A)
N u có R và I, có th tính hi u đi n th nh sau :ế ể ệ ệ ế ư
UAB = VA - VB = I.R ; I.R: g i là đ gi m th (đ s t th hay s t áp) trên đi n tr . ọ ộ ả ế ộ ụ ế ụ ệ ở
Công th c c a đnh lu t ôm cũng cho phép tính đi n tr :ứ ủ ị ậ ệ ở
Trang 4
Δq
I = Δt
A
I
R
I
U
A B
I
OU
I
U
R
()
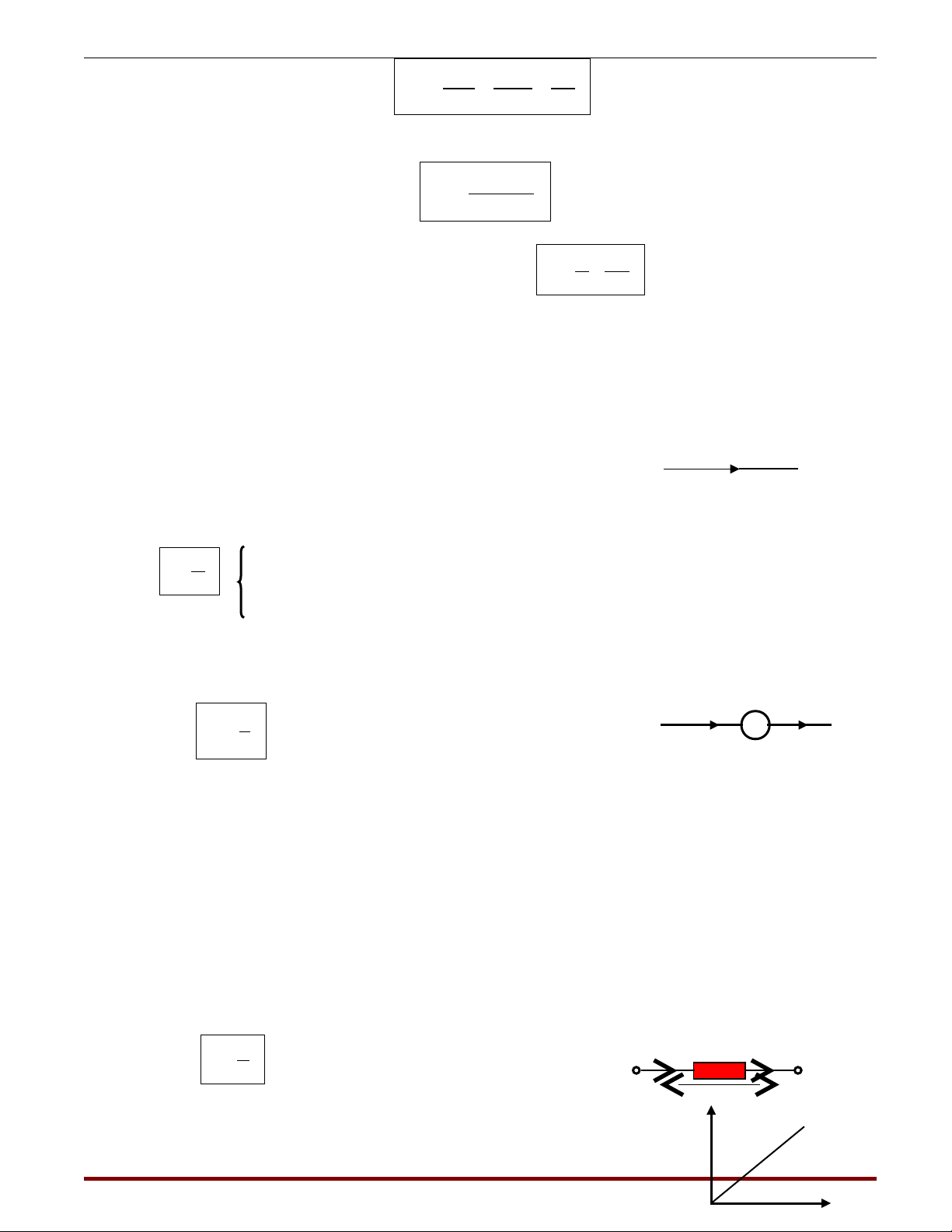
2) Đc tuy n V - A (vôn - ampe)ặ ế
Đó là đ th bi u di n I theo U còn g i là đng đc tr ng vôn - ampe. ồ ị ể ễ ọ ườ ặ ư
Đi v i v t d n kim lo i (hay h p kim) nhi t đ nh t đnhố ớ ậ ẫ ạ ợ ở ệ ộ ấ ị
đc tuy n V –A là đo n ặ ế ạ
đng th ng qua g c các tr c: R có giá tr không ph thu c U. ườ ẳ ố ụ ị ụ ộ
(v t d n tuân theo đnh lu t ôm).ậ ẫ ị ậ
Ghi chú : Nh c l i k t qu đã tìm hi u l p 9.ắ ạ ế ả ể ở ớ
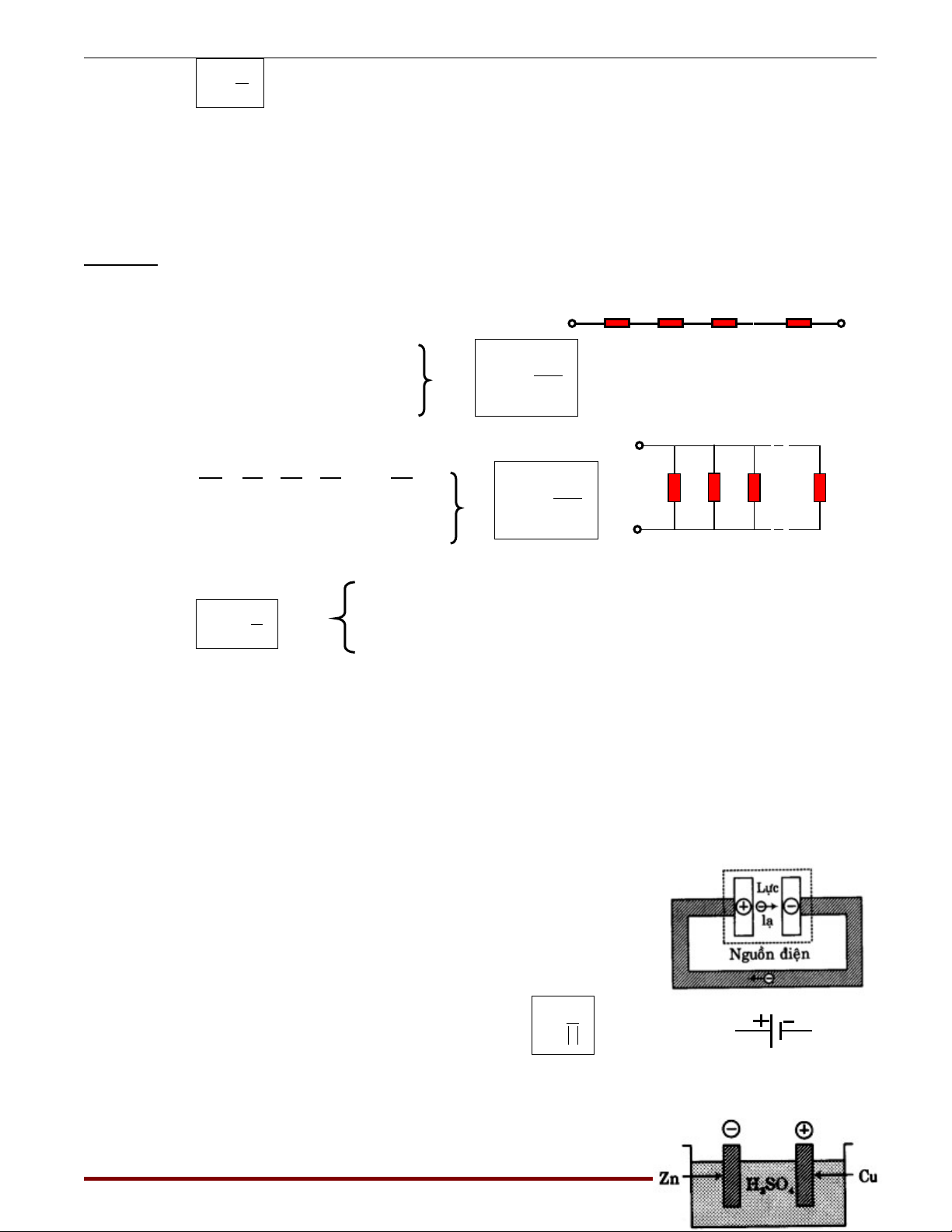
a) Đi n tr m c n i ti p:ệ ở ắ ố ế
đi n tr t ng đng đc tính b i:ệ ở ươ ươ ượ ở
Rm = Rl + R2+ R3+ … + Rn
Im = Il = I2 = I3 =… = In
Um = Ul + U2+ U3+… + Un
b) Đi n tr m c song song:ệ ở ắ
đi n tr t ng đng đc anh b i:ệ ở ươ ươ ượ ở
1 2 3
1
m n
R+ + + +���
1 1 1 1
=R R R R
Im = Il + I2 + … + In
Um = Ul = U2 = U3 = … = Un
c) Đi n tr c a dây đng ch t ti t di n đu:ệ ở ủ ồ ấ ế ệ ề
: đi n tr su t (ệ ở ấ m)
S
l
R
l: chi u dài dây d n (m)ề ẫ
S: ti t di n dây d n (mế ệ ẫ 2)
III. NGU N ĐI NỒ Ệ :
Ngu n đi n là thi t b t o ra và duy trì hi u đi n th đ duy trì dòng đi n. M i ngu n đi nồ ệ ế ị ạ ệ ệ ế ể ệ ọ ồ ệ
đu có hai c c, c c d ng (+) và c c âm (-).ề ự ự ươ ự
Đ đn gi n hoá ta coi bên trong ngu n đi n có l c l làm di chuy n các h t t i đi n (êlectron;ể ơ ả ồ ệ ự ạ ể ạ ả ệ
Ion) đ gi cho:ể ữ
* m t c c luôn th a êlectron (c c âm).ộ ự ừ ự
* m t c c luôn thi u lectron ho c th a ít êlectron h n bên kia (c c d ng).ộ ự ế ẽ ặ ừ ơ ự ươ
Khi n i hai c c c a ngu n đi n b ng v t d n kim lo i thì cácố ự ủ ồ ệ ằ ậ ẫ ạ
êlectron t c c (-) di chuy n qua v t d n v c c (+).ừ ự ể ậ ẫ ề ự
Bên trong ngu n, các êlectron do tác d ng c a l c l di chuy n tồ ụ ủ ự ạ ể ừ
c c (+) sang c c (-). L c l th c hi n công (ch ng l i công c n c aự ự ự ạ ự ệ ố ạ ả ủ
tr ng tĩnh đi n). Công này đc g i là công c a ngu n đi n.ườ ệ ượ ọ ủ ồ ệ
Đi l ng đc tr ng cho kh năng th c hi n công c a ngu nạ ượ ặ ư ả ự ệ ủ ồ
đi n g i là su t đi n đng E đc tính b i:ệ ọ ấ ệ ộ ượ ở
q
A
(đn v c a ơ ị ủ E là V)
trong đó : A là công c a l c l làm di chuy n đi n tích t c c này sang c c kia. c a ngu n đi n.ủ ự ạ ể ệ ừ ự ự ủ ồ ệ
|q| là đ l n c a đi n tích di chuy n. ộ ớ ủ ệ ể
Ngoài ra, các v t d n c u t o thành ngu n đi n cũng có đi n trậ ẫ ấ ạ ồ ệ ệ ở
g i là đi n tr trong r c a ngu n đi n. ọ ệ ở ủ ồ ệ
Trang 5
Rn
R3
R2
R1
R1R2R3Rn
m
m
m
U
I = R
m
m
m
U
I = R


























