CHUYÊN ĐỀ ĐIỆN TÍCH – ĐIỆN TRƢỜNG
1. Vấn đề liên quan đến lực điện
Bài 1: Hai quả cầu nhỏ giống nhau bằng kim loại, có khối lượng 5 g, được treo vào cùng một điểm O
bằng hai sợi dây không dãn, dài 10 cm. Hai quả cầu tiếp xúc với nhau. Tích điện cho một quả cầu thì thấy
hai quả cầu đẩy nhau cho đến khi hai dây treo hợp với nhau một góc 60°. Tính điện tích đã truyền cho quả
cầu. Lấy g = 10 m/s2.
Bài 2: Trên đường thẳng xy cho bốn điểm O, A, B, C theo thứ tự từ trái qua phải, trong đó B là trung
điểm của AC. Đặt điện tích Q tại O. Sau đó lần lượt đặt điện tích q tại A, B và C. Biết rằng khi q đặt tại A
và B thì lực tương tác giữa hai điện tích là
4
19.10FN
và
4
24.10FN
. Tìm lực tương tác giữa các
điện tích khi q đặt tại C.
Bài 3: Hai quả cầu nhỏ xem như là hai chất nhiễm điện như nhau q1=q2=1,6.10-8 C
Khối lượng hai quả cầu như nhau và bằng m=0,6g. Hai quả cầu được treo vào hai sợi dây mảnh-nhẹ
đều có chiều dài l=60cm. Hai đầu dây còn lại treo vào cùng một điểm. Cả hệ thống đặt trong môi
trường không khí (sinα≈tanα)
a/ Nếu điểm treo cố định, hãy tính khoảng cách 2 quả cầu.
b/ Cho điểm treo chuyển động xuống phía dưới theo phương đứng với gia tốc nhanh dần đều
5m/s2 . Hãy tính lại khoảng cách hai quả cầu.
Giải
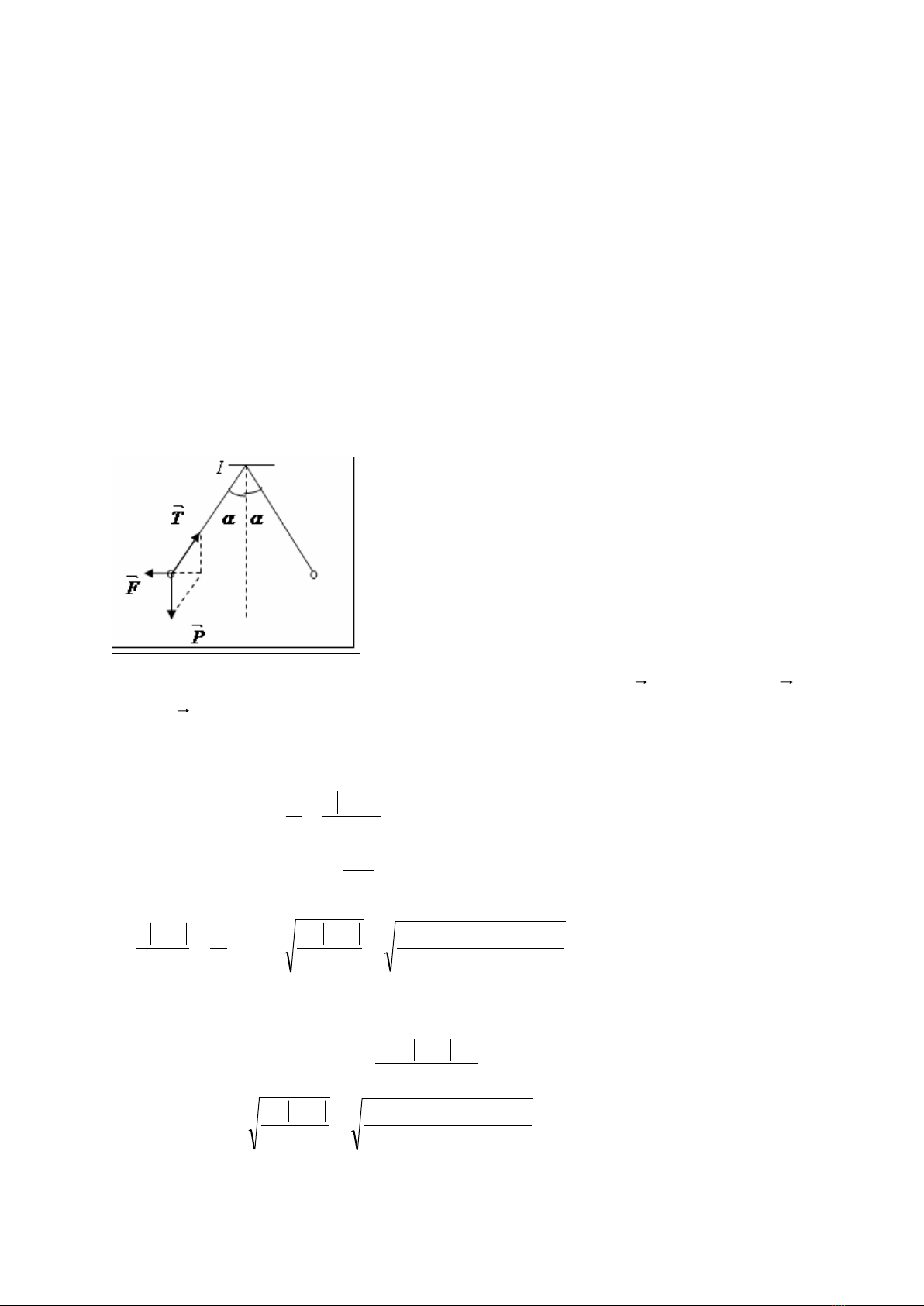
+ Khi hệ đứng cân bằng mỗi quả cầu chịu tác dụng của 3 lực: Trọng lực ; Lực đẩy culông ; Sức
căng dây
0F P T+ + =
r r r
+ Xét một quả cầu thì các lực biểu diễn như hình vẽ.
Ta có: ; b: là khoảng cách hai điện tích (m)
+ Từ (1) và (2)
b,
+ Khi điểm treo chuyển động nhanh dần đều xuống phía dưới với gia tốc a thì mỗi quả cầu chịu thêm lực
quán tính hướng lên trên.
Lúc đó biểu thức (1) trở thành:
+ Từ (2) và (3)
Bài 4. Hai quả cầu nhỏ giống hệt nhau, mỗi quả có khối lượng 5 g, mang điện tích q được treo vào điểm
O bởi hai sợi dây có cùng chiều dài 50 cm. Cả hệ được đặt trong không khí. Khi cân bằng các dây treo
hợp với nhau một góc 90o. Lấy g = 10 m/s2.
P
F
T
(2)
(1)
l
b
tg
bgm
qqk
P
F
tg
2/
sin
..
..
2
21
cmm
mg
qqlk
b
l
b
mgb
qqk (72,7)(0772,0
10.10.6,0
)10.6,1.(10.9.6,0.2
2
2
.33
289
321
2
21
(3)
2
21
).(
.
bmamg
qqk
tg
)(7,9)(097,0
)510(10.6,0
)10.6,1.(6,0.10.9.2
)(
2
3
289
321 cmm
agm
qqkl
b
1. Tính giá trị của q và lực căng dây treo khi cân bằng.
2.Kéo điểm treo O chuyển động nhanh dần đều lên trên theo phương thẳng đứng với gia tốc a. Khicân
bằng hai dây treo hợp với nhau một góc 60o. Bỏ qua lực cản không khí. Tính a.
4 điểm
F, T và mg cân bằng
T =
2mg
= 0,07 N
F = mg =
2
2
9
2
2
9
)25,0(
q
10.9
)2(
q
10.9
q = ∓1,67.10-6 C
Xét trong hệ qui chiếu gắn với O, các quả cầu chịu thêm lực quán tính Fq =
ma
F =
2
2
9o q
10.9
3
mamg
30tan)mamg(
(1)
Theo ý 1.1 thì
mg2
q
10.9 2
2
9
(2)
(1) và (2) => a =
g)132(
= 24,6 m/s2.
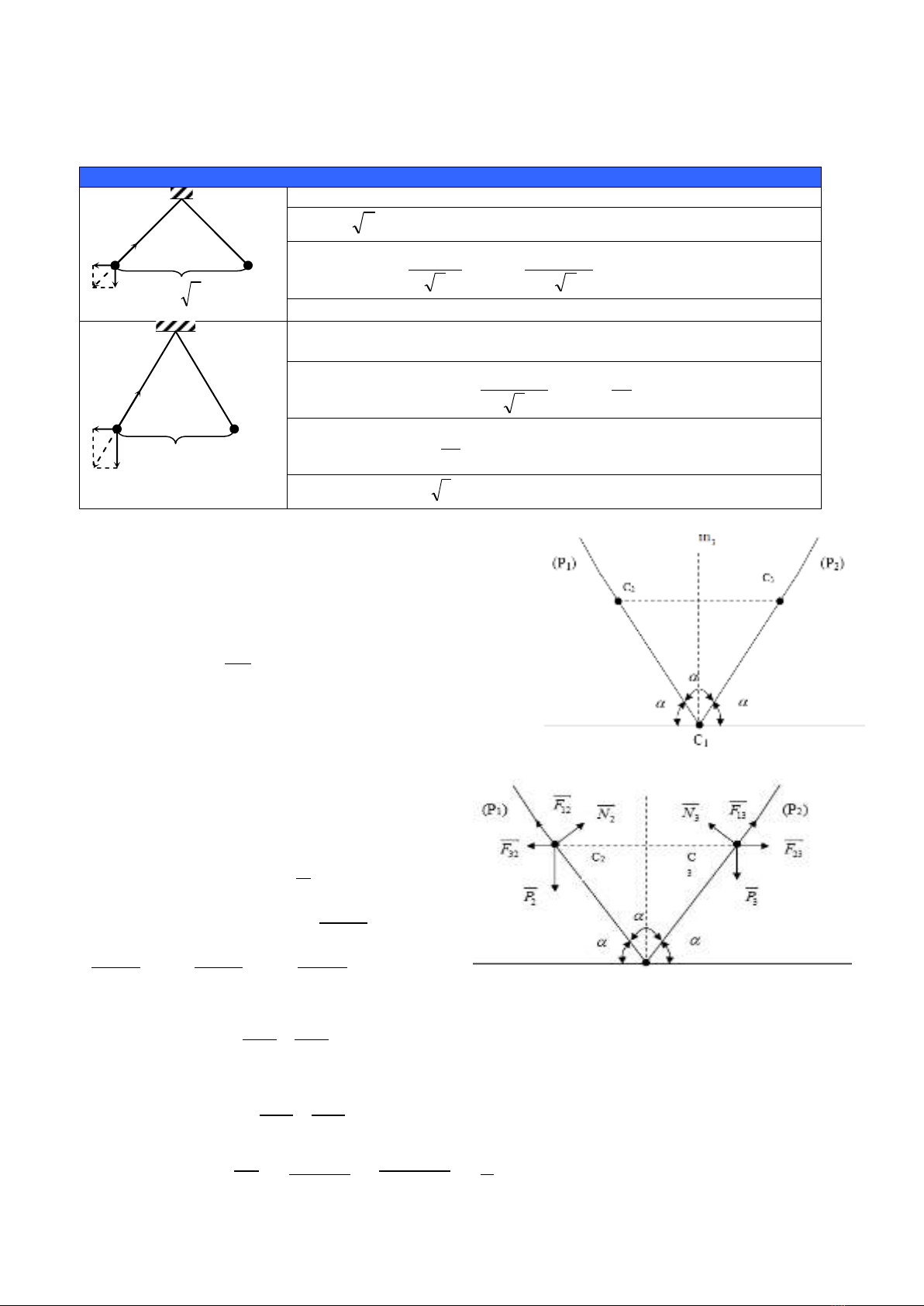
Bài 5. Cho hệ như ở hình vẽ: (
1
P
),(
2
P
) là hai tấm thủy tinh
phẳng nhẵn;
= 60o; C1,C2,C3 là ba quả cầu nhỏ tích điện
cùng dấu
(
1 2 3
,,q q q
).Khi cân bằng
23
C , C
ở cùng độ cao.Biết rằng
1 2 3
2.q q q
Tìm
2
3
m
m
của
23
C , C
.
G
. Khi cân bằng
C1C2C3 đều
C1C2 = C1C3 = C2C3
= l.
. Fms = 0. các lực tác dụng lên C2, C3 khi cân bằng như
biểu diễn ở hình vẽ.
. Gọi q1= q2 = nq3 = q và q3 =
q
n
.
. P2 = m2g ; P3 = m3g ; F12 =
12
2
Kq q
l
; F32 =
32
2
Kq q
l
; F13=
13
2
Kq q
l
; F23 =
23
2
Kq q
l
Viết phương trình cân bằng lực cho C2, C3 theo phương P1 và P2 ta có:
m2g sin
=
22
22
os
Kq Kq c
l nl
(1)
m3g sin
=
22
22
os
Kq Kq c
nl nl
(2)
Từ (1) và (2) suy ra:
2
3
m
m
=
os
1 os
nc
c
=
0
0
2 os60
1 +cos60
c
=
5
3
.
mg + ma
ℓ
O
T
O
T
2
F
mg
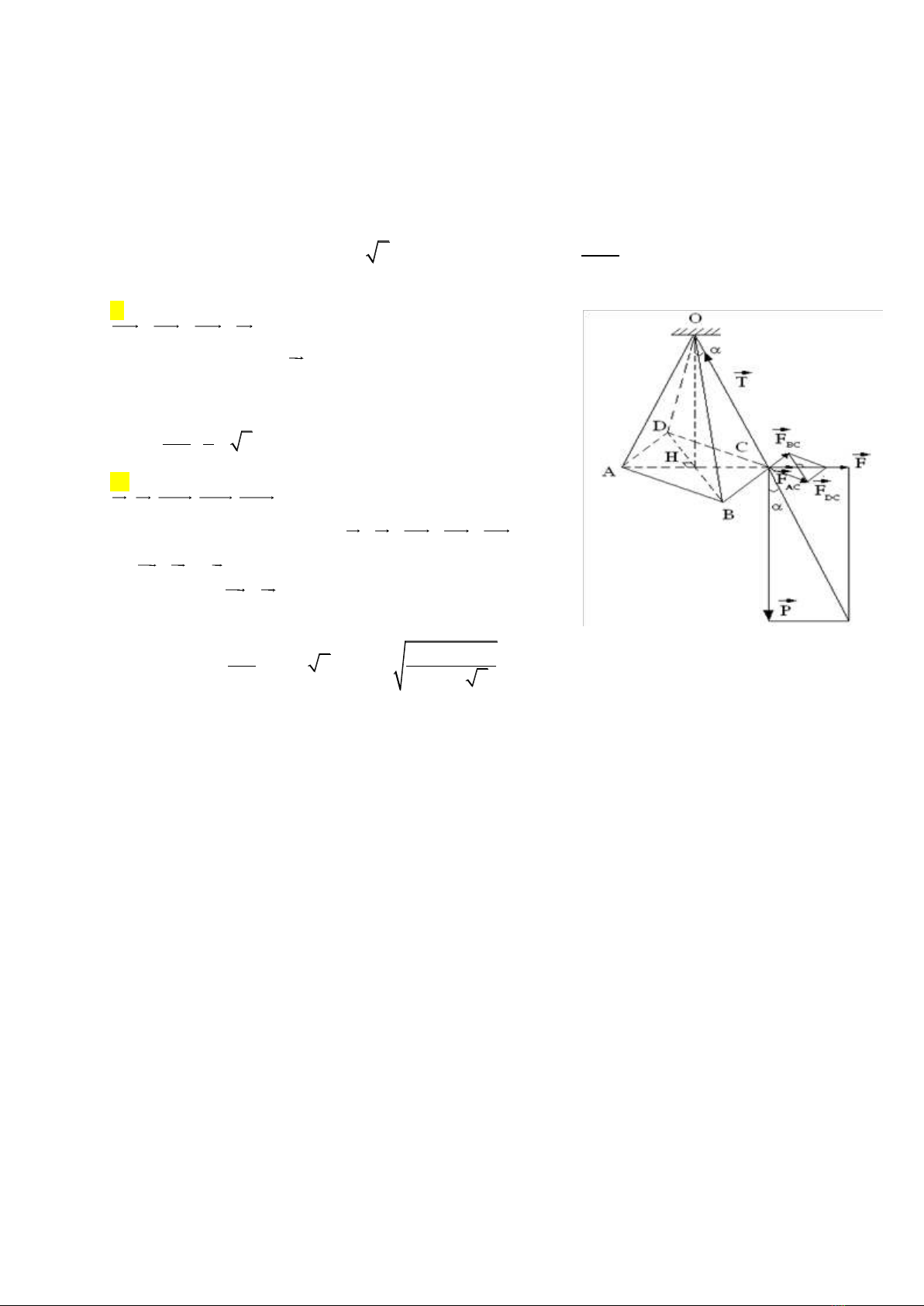
Bài 6. Có 4 quả cầu nhỏ giống hệt nhau, mỗi quả có khối lượng m, điện tích q. Treo 4 quả vào điểm O
bằng 4 sợi dây mảnh cách điện dài l. Khi cân bằng, bốn điện tích nằm tại 4 đỉnh của hình vuông ABCD
cạnh a=l.
a) Tính lực điện do ba điện tích đặt tại A, B, D tác dụng lên điện tích đặt tại C theo q, l và hằng số
điện k.
b) Tính giá trị của q theo m, l và gia tốc trọng trường g.
Áp dụng bằng số: l=20cm, m=
(1 2 2)
gam, g=10m/s2, k=
2
9
2
9.10 ( )
Nm
C
.
Giải
a) Lực tác dụng vào điện tích đặt tại C như hình vẽ.
AC BC DC
F F F F
(1)
Do tính đối xứng nên lực
F
cùng chiều với AC
Chiếu phương trình (1) lên phương AC ta được:
F = FAC + FDCcos450 + FBCcos450
2
2
kq 1
F2
2l
b) Xét quả cầu C. Các lực tác dụng vào quả cầu gồm:
, , , ,
AC BC DC
T P F F F
.
Tại vị trí cân bằng của quả cầu C:
0
AC BC DC
T P F F F
F P T
(như hình vẽ)
Hợp lực của
FP
phải có phương của dây treo OC.
Do =450 nên
22
20,5 2 (0,5 2)
kq mgl
F P mg q
lk
Thay số:
7
3.10qC
.
Bài 7: Cho 3 điện tích điểm giống nhau +q đặt tại 3 đỉnh 1 tam giác đều ABC. Điện tích +q1 đặt tại M
nằm trên đường thẳng đi qua trọng tâm G của tam giác và vuông góc với mặt phẳng tam giác, cách M một
đoạn x, trong chân không.
a) Xác định độ lớn lực tác dụng lên q1.
b) Tìm x để độ lớn lực tác dụng lên q1 cực đại.
c) Nếu để cho 3 điện tích q bắt đầu chuyển động tự do ra xa nhau (không có q1). Tìm vận tốc cực
đại của chúng. Cho khối lượng mỗi điện tích là m. Bỏ qua ma sát, trọng lực
Bài 8: Hai quả cầu kim loại nhỏ giống nhau được treo vào một điểm bởi hai sợi dây nhẹ không dãn, dài
= 40 cm. Truyền cho hai quả cầu điện tích bằng nhau có điện tích tổng cộng q = 8.10-6 C thì chúng đẩy
nhau các dây treo hợp với nhau một góc 900. Lấy g = 10 m/s2.
a. Tìm khối lượng mỗi quả cầu.
b. Truyền thêm điện tích q’cho một quả cầu, thì thấy góc giữa hai dây treo giảm đi còn 600. Xác định
cường độ điện trường tại trung điểm của sợi dây treo quả cầu được truyền thêm điện tích này?
Bài 9: Cho 2 quả cầu nhỏ giống nhau có cùng điện tích q được treo cạnh nhau bằng 2 sợi dây mảnh
không dãn, dài như nhau trong không khí. Khi hai quả cầu cân bằng mỗi sợi dây lệch khỏi phương thẳng
đứng một góc
. Nhúng hệ hai quả cầu trên vào trong dầu có hằng số điện môi bằng 2, góc lệch của mỗi
dây treo vẫn là
. Tìm khối lượng riêng của mỗi quả cầu, biết khối lượng riêng của dầu là
33 /10.8,0 mkg
2.Vấn đề liên quan đến điện trƣờng
Bài 1: Hai điện tích q1 = q2 = q >0 đặt tại hai điểm A và B trong không khí. Cho biết AB = 2a.
a) Xác định cường độ điện trường tại điểm M trên đường trung trực của AB cách AB một đoạn h.
b) Tìm h để EM cực đại. Tính giá trị cực đại này. GIẢI
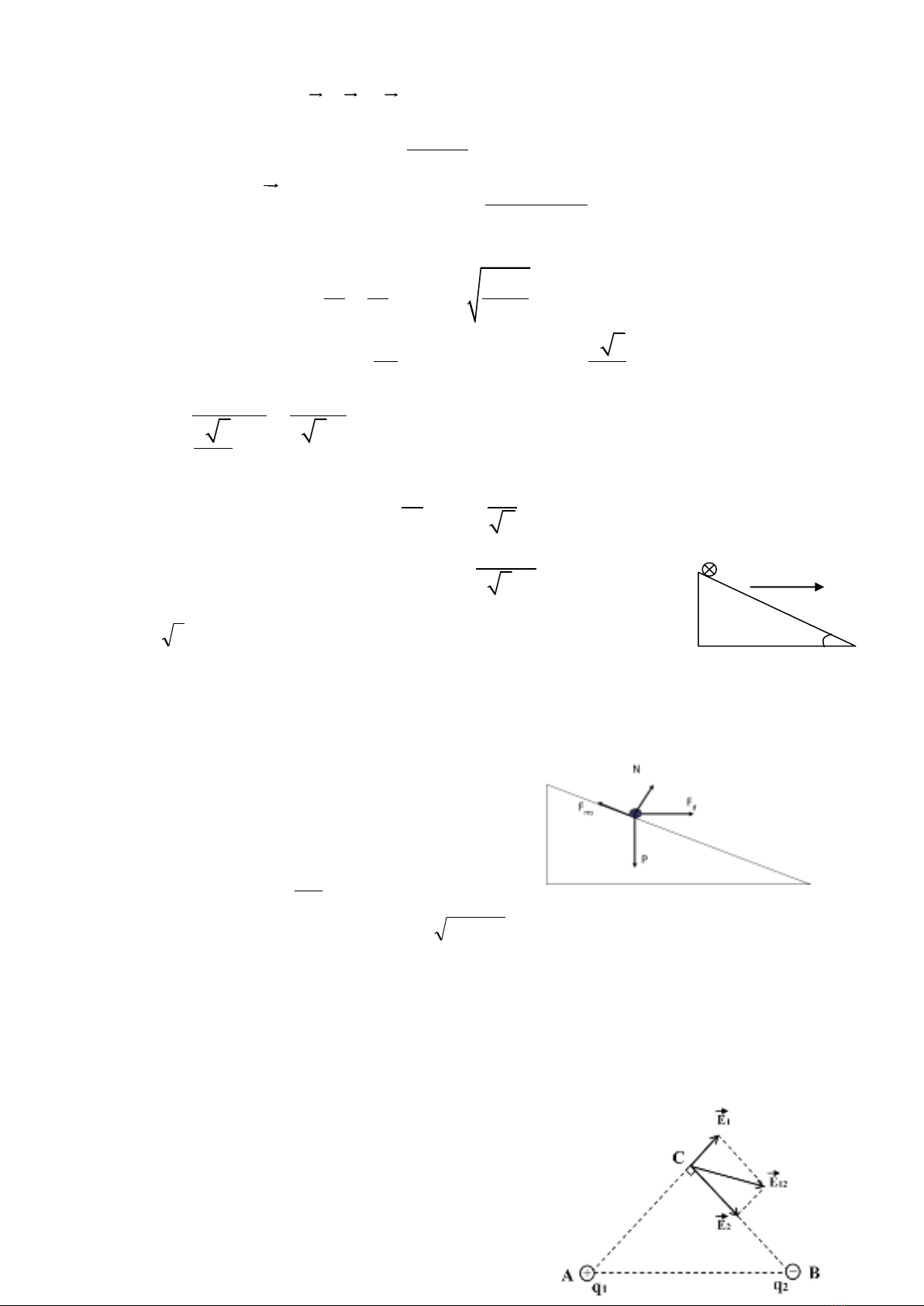
a) Cường độ điện trường tại M:
12
E E E
12 22
q
E E k ah
...........
Hình bình hành xác định
E
là hình thoi: E = 2E1cos
3/2
22
2kqh
ah
....
b) Định h để EM đạt cực đại:
2 2 4 2
2 2 2 3
3 3/2
2 2 4 2 2 2 2
a a a .h
a h h 3.
2 2 4
27 3 3
a h a h a h a h
42
Do đó:
M2
2
2kqh 4kq
E3 3 3 3a
ah
2
EM đạt cực đại khi:
2
2
Mmax 2
aa
h h .........................
22
4kq
E ..........................
3 3.a
i 2: Một quả cầu nhỏ khối lượng m = 10g mang điện tích
dương q=
.3
10-7C được thả không vận tốc đầu từ đỉnh B của mặt phẳng
nghiêng BC=20cm và hợp với phương ngang góc α=300. Hệ thống
được đặt trong một điện trường đều E=105V/m có đường sức nằm
ngang như hình vẽ . Cho hệ số ma sát giữa vật và mặt phẳng nghiêng
là µ=0,2, tính vận tốc của quả cầu ở chân mặt phẳng nghiêng. Lấy
g=10m/s2.
Giải
- Theo phương vuông góc với mặt phẳng nghiêng ta có:
P.cosα = N + Fđ. sinα N = mg.cosα – q.E.sinα (1)
- Theo phương chuyển động của vật:
mg.sinα + Fđ.cosα - µN = ma (2)
Thay (1) và (2) và biến đổi ta được:
a = g.(sinα - µcosα) +
m
qE
.(cosα+µsinα) ≈ 4,94m/s2
Vận tốc của vật ở chân mặt phẳng nghiêng là: v =
2.a.BC
≈ 1,4m/s
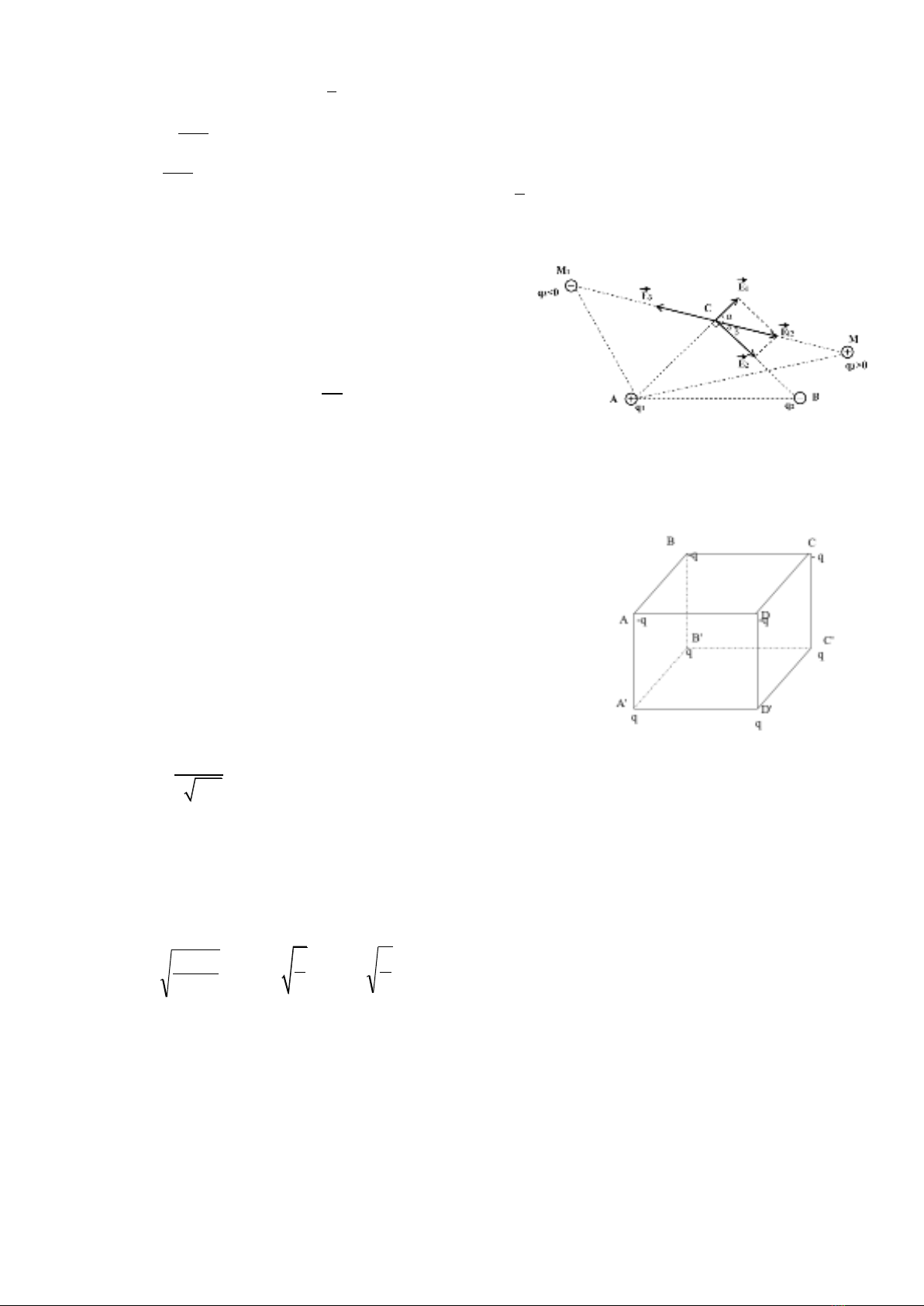
Bài 3. Cho hai điện tích điểm q1=3.10-8C; q2=-6.10-8C đặt tại A, B trong không khí; AB= a =20cm.
a. Xác định vectơ cường độ điện trường tổng hợp tại C. Biết CA=CB;
.
b. Phải đặt điện tích điểm | |=9.10-8C cách A một khoảng bằng bao nhiêu để vectơ cường độ
điện trường tổng hợp do điện tích q1, q2, q3 gây ra tại C bằng không
Giải
α
E
m
B
E
C
A
√
| |
| |
√
- α=63026’ ; β=26034’
b.
- Hình vẽ
: Vectơ cường độ điện trường do điện tích q3 gây ra tại C.
-
-
| |
* Trường hợp: q3=
-
- AM=25,98 cm
* Trường hợp: q3=
-
- AM1=16,15cm
Bài 4. Tại 8 đỉnh của hình lập phương cạnh a =0,2m ở trong chân
không, có đặt 8 điện tích điểm có cùng độ lớn là q = 9.0-8, bốn điện
tích ở đáy trên có trị số âm, bốn điện tích đáy dưới có trị số dương.
Xác định cường độ điện trường tại tâm hình lập phương.
ĐS:
5
2
32 1,25.10 /
33
kq
E V m
a
Bài 5. Một vòng dây hình tròn bán kính R mang điện tích Q phân bố đều và nằm có định trong một mặt
phẳng thẳng đứng. Một điện tích q (cùng dấu với Q) có khối lượng m nằm cân bằng tại một điểm ở trục
vòng dây. Điện tích q được gắn ở đầu một sợi chỉ mảnh cách điện, còn đầu kia của sợi dây buộc vào điểm
cao nhất của vòng dây. Toàn bộ đặt trong trường trọng lực.
a) Hãy tìm chiều dài cần thiết của sợi dây đó
b) Nếu điện tích q nằm ở vị trí mà lực điện tác dụng lên nó là lớn nhất thì chiều dài và lực căng dây
ở vị trí đó bằng bao nhiêu?
ĐS: a.
3
mg
kQqR
; b.
3
2
l
.R ; T=
2
3
.mg
Bài 6. trong một điện trường tạo bởi một điện tích điểm +q1 và một điện tích điểm -q2, có một đường sức
xuất hiện từ +q1 hợp với đoạn thẳng nối hai điện tích một góc
a. Hãy tính góc
mà đường sức đó hợp với đoạn thẳng trên tại -q2


























