http://laisac.page.tl
ChuyênĐề
T
T
TH
H
HỂ
Ể
ỂT
T
TÍ
Í
ÍC
C
CH
H
H
LưuTuấnHiệp
GVTHPTLaiVung2
Phaàn I. THEÅ TÍCH KHOÁI CHOÙP – KHOÁI LAÊNG TRUÏ
Trong tröôøng phoå thoâng , Hình hoïc Khoâng gian laø moät baøi toaùn raát khoù ñoái vôùi hoïc
sinh, do ñoù hoïc sinh phaûi ñoïc thaät kyõ ñeà baøi vaø töø ñoù xaùc ñònh giaû thuyeát baøi toaùn, veõ
hình roài tieán haønh giaûi baøi toaùn.
Cả hai chương trình chuẩn vaø naâng caođềuđề cậpđến theå tích cuûa khoái ña dieän (
theå tích khoái choùp, khoái laêng truï).
Thoâng thöôøng baøi toaùn veà hình choùp ñöôïc phaân thaønh 2 daïng nhö sau:
Cho hình choùp
Hình choùp coù caïnh beân vuoâng goùc vôùi maët
phaúng ñaùy
A C
B
S
Ña giaùc ñaùy :
- Tam giaùc vuoâng
- Tam giaùc caân
- Tam giaùc ñeàu
- Hình vuoâng, chöõ nhaät
ToaùnĞįİ TheåTíchKhoáiÑaDieän –MaëtTroønXoay
Taøi lieäu löu haønh noäi boä 1LöuTuaán
Hieäp
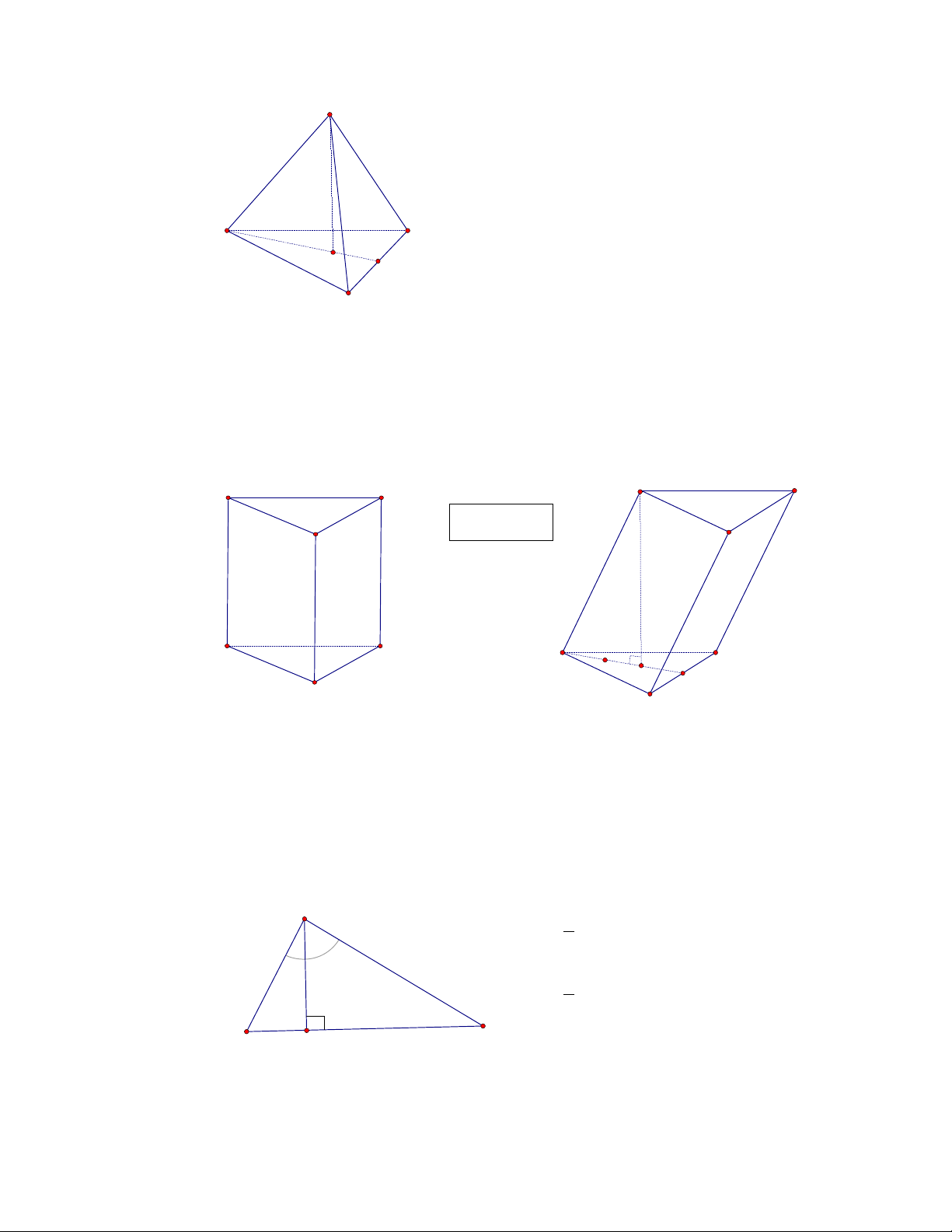
Hình choùp ñeàu
A
C
B
S
O
- Hình choùp tam giaùc ñeàu
- Hình choùp töù giaùc ñeàu
Thoâng thöôøng baøi toaùn veà hình laêng truï:
. V B h =
B: dieän tích ñaùy
h : ñöôøng cao
Laêng truï ñöùng ABC.A
1
B
1
C
1 Laêng truï xieân ABC.A
1
B
1
C
1
A1A ^ (ABC) A1G ^ (ABC)
HEÄ THOÁNG KIEÁN THÖÙC CÔ BAÛN
A.CácTínhChất:
a.Tamgiác:
- Diệntíchcủatamgiác
*
µ
1. . .sin
2
ABC
S AB AC A
D =
*1. .
2
ABC
S BC AH
D =
- Cáctamgiácđặcbiệt:
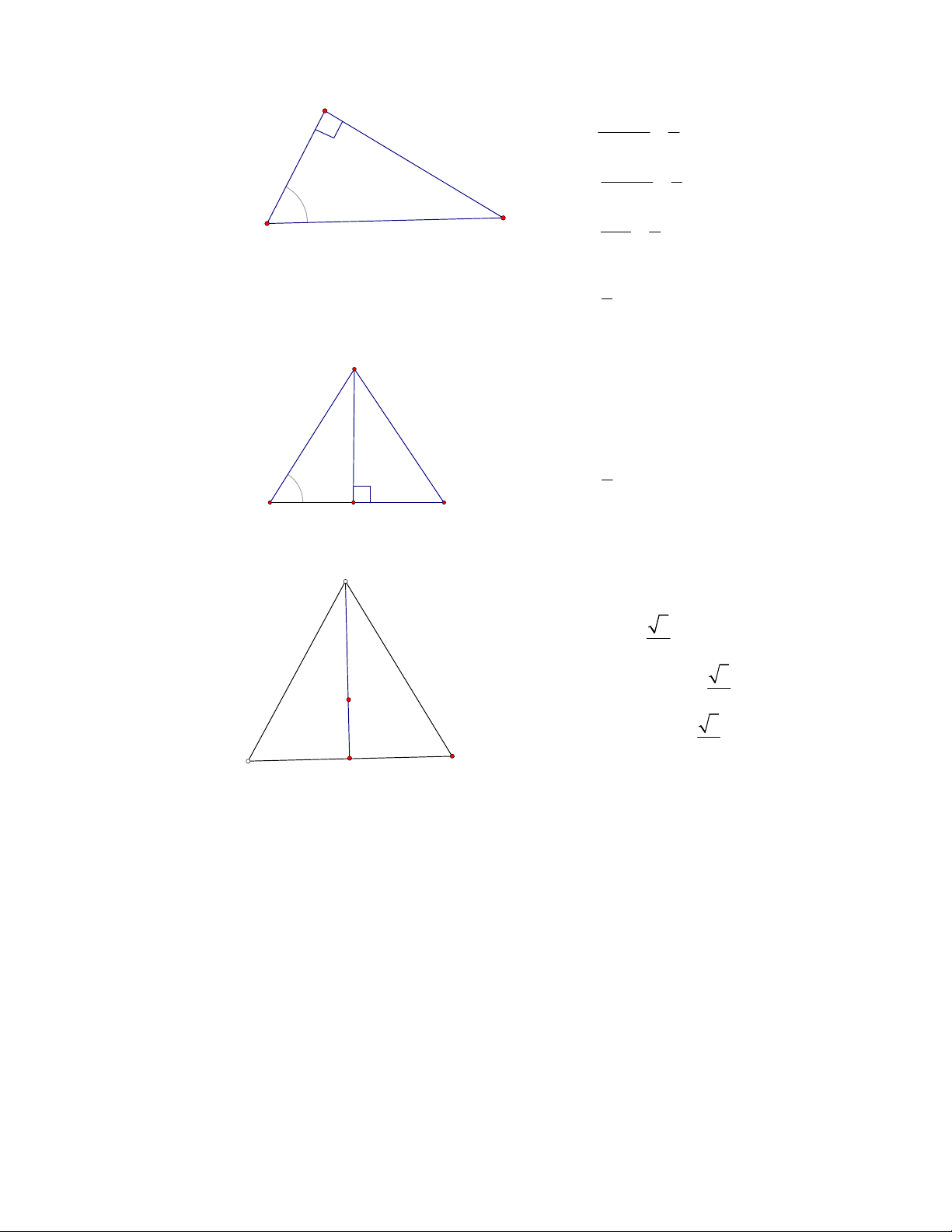
o Tamgiácvuông:
h
H
A
B C
A C
B
B1
C1
A1
H
A1
B
CA
B1
C1
G
ToaùnĞįİ TheåTíchKhoáiÑaDieän –MaëtTroønXoay
Taøi lieäu löu haønh noäi boä 3LöuTuaánHieäp
+Địnhlýpitago: 2 2 2
BC AB AC = +
+Tỷsốlượnggiáctrongtamgiácvuông
µ
= =
Ñoái
sin Huyeàn
b
B a
µ
= =
Keà
cos Huyeàn
c
B a
µ
= =
Ñoái
tan Keà
b
B c
+Diệntíchtamgiácvuông:
1. .
2
ABC
S AB AC
D =
o Tamgiáccân:
+ Đường cao AH cũng là đường trung
tuyến
+Tínhđườngcaovàdiệntích
µ
.tanAH BH B =
1. .
2
ABC
S BC AH
D =
o Tamgiácđều
+Đườngcaocủatamgiácđều
= = 3
. 2
h AM AB
(đườngcaoh=cạnh x 3
2)
+Diệntích: 2 3
( ) . 4
ABC
S AB
D =
c
a
b
C
B
A
A
B C
H
B
A
G
C
M
ToaùnĞįİ TheåTíchKhoáiÑaDieän –MaëtTroønXoay
Taøi lieäu löu haønh noäi boä 4LöuTuaánHieäp
b.Tứgiác
- Hìnhvuông
+Diệntíchhìnhvuông:
2
( )
ABCD
S AB =
(Diệntíchbằngcạnhbìnhphương)
+Đườngchéohìnhvuông
= = . 2 AC BD AB
(đườngchéohìnhvuôngbằngcạnhx 2)
+OA=OB=OC=OD
- Hìnhchữnhật
+Diệntíchhìnhvuông:
.
ABCD
S AB AD =
(Diệntíchbằngdàinhânrộng)
+Đườngchéohìnhchữanhật bằngnhauvà
OA=OB=OC=OD
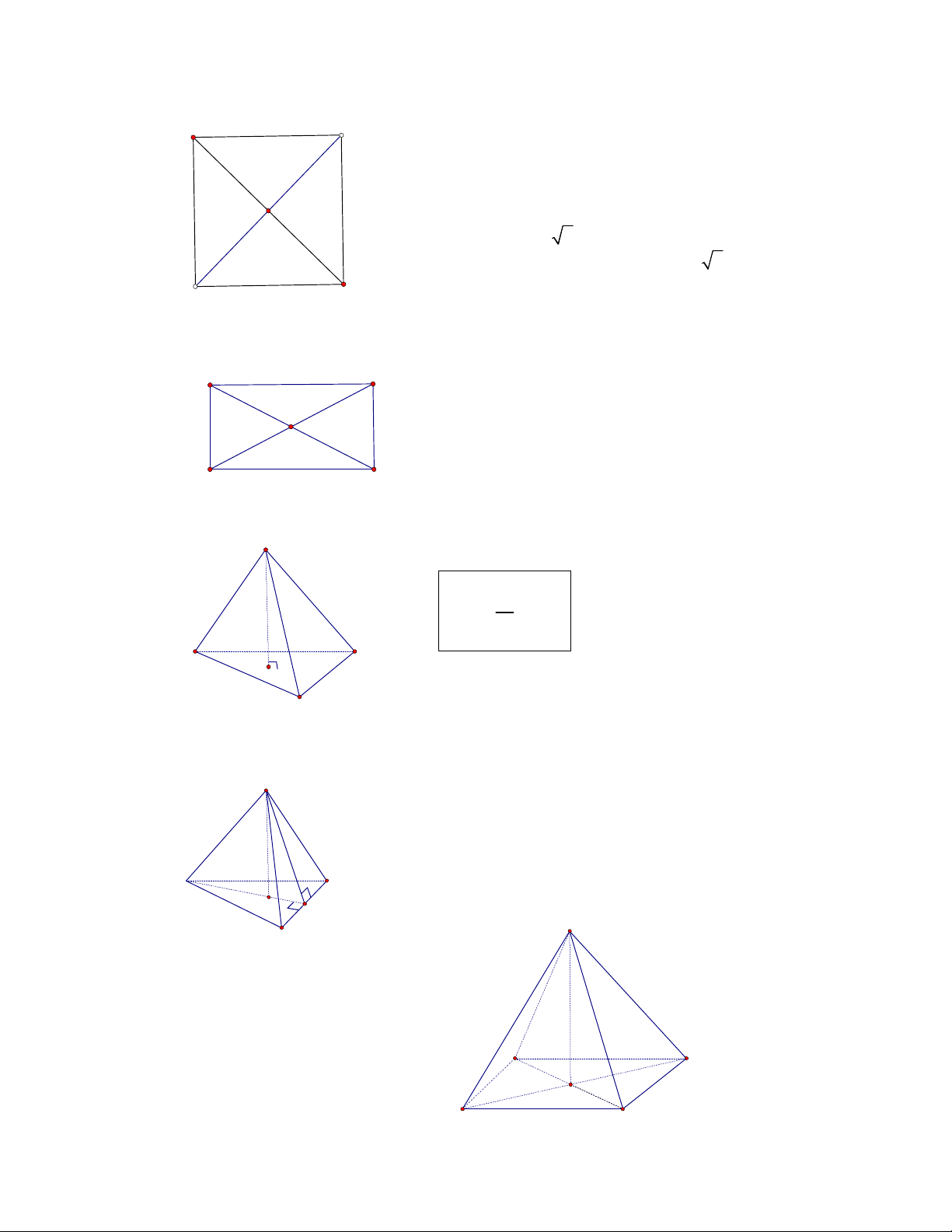
B. ThểTíchKhốiChóp:
+Thểtíchkhốichóp
= 1 . .
3
V B h
Trongđó:Blàdiệntíchđagiácđáy
h:làđườngcaocủahìnhchóp
Cáckhốichópđặcbiệt:
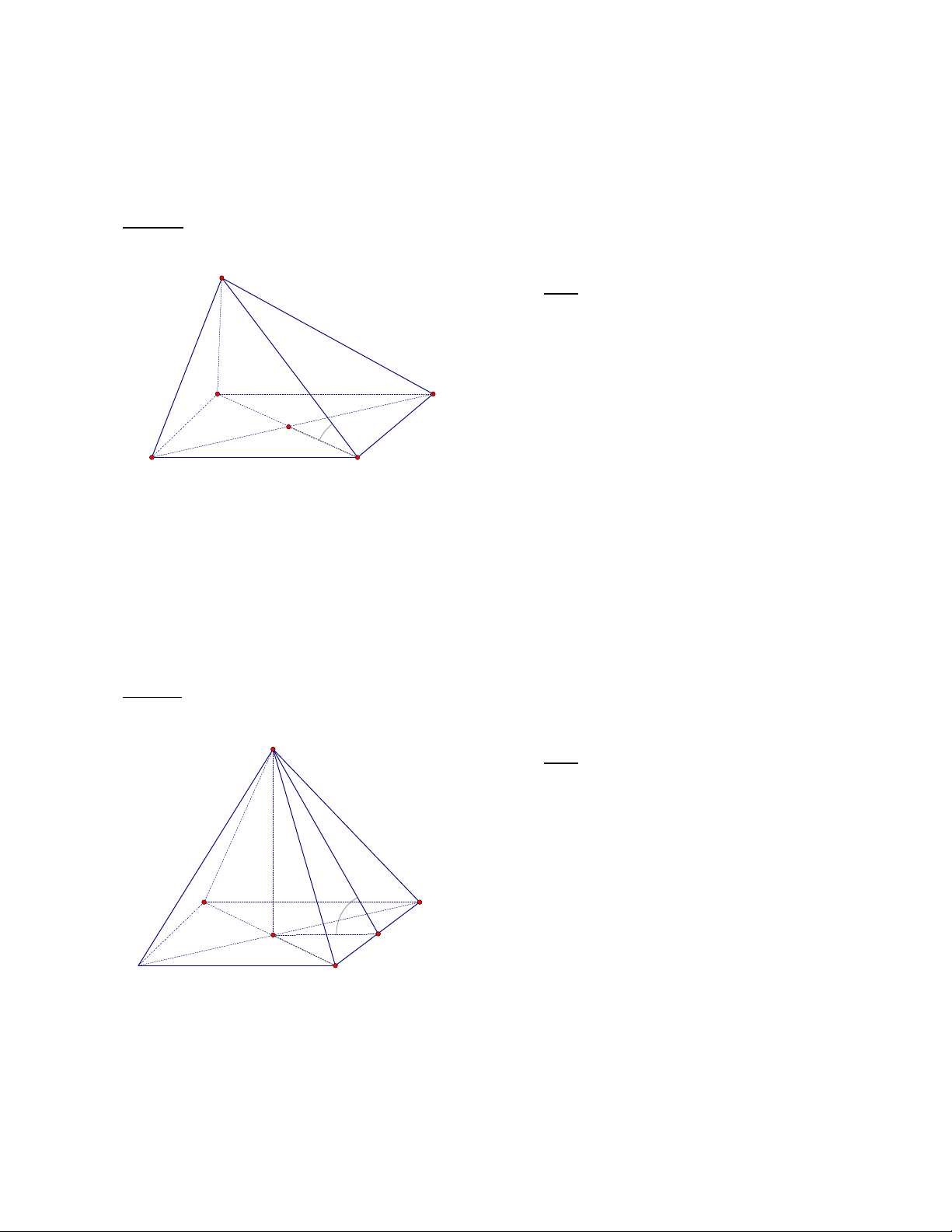
- Khốitứdiệnđều:
+Tấtcảcáccạnhđềubằngnhau
+Tấtcảcácmặtđềulàcáctamgiácđều
+Olàtrọngtâmcủatamgiácđáy
VàAO ^(BCD)
B
- Khốichóptứgiácđều
+Tấtcảcáccạnhbênbằngnhau
+ĐagiácđáylàhìnhvuôngtâmO
+SO ^(ABCD)
O
B
D
A
C
O
A B
D C
h
S
B
A
C
H
A
C
D
M
O
O
C
D
B
A
S
ToaùnĞįİ TheåTíchKhoáiÑaDieän –MaëtTroønXoay
Taøi lieäu löu haønh noäi boä 5LöuTuaánHieäp
C.Góc:
Cáchxácđịnhgóc
- Gócgiữađườngthẳngdvàmặtphẳng(P):
o Tìmhìnhchiếud
/ củadlênmặtphẳng(P)
o Khiđógócgiữadvà(P)làgócgiữadvàd
/
Vídụ1:ChohìnhchópS.ABCDcóABCDlàhìnhvuông,SAvuônggócvới(ABCD)và
gócgiữaSCvới(ABCD)bằng45
0
.Hãyxácđịnhgócđó.
Giải
Tacó: = ( ) ABCD
AC hc SC
Þ
·
·
·
= = = ( ,( )) ( , ) 45
o
SC ABCD SC AC SCA
- Gócgiữahaimặtphẳng(P)và(Q):
o Xácđịnhgiaotuyếndcủa(P)và(Q)
o Tìmtrong(P) đườngthẳnga ^(d),trongmặtphẳng(Q)đườngthẳngb ^(d)
o Khiđógócgiữa(P)và(Q)làgócgiữahaiđườngthẳngavàb
Vídụ2:ChohìnhchóptứgiácđềuS.ABCDcóABCDlàhìnhvuông,vàgócgiữamặtbên
vớimặtđáybằng60
0
.Hãyxácđịnhgócđó.
Giải
GọiMlàtrungđiểmBC
Tacó:
(SBC) Ç (ABCD) = BC
(ABCD)ÉAM ^ BC
(SBC) ÉSM ^BC
(vì ( )
SM
ABCD
AM hc = )
Þ
·
·
·
(( ),( )) ( , ) 60
o
SBC ABCD SM AM SMA = = =
45O
S
C
D
B
A
60
M
O
S
A B
C


























