ĐẠI HỌC BÁCH KHOA ĐÀ NẴNG
KHOA CÔNG NGHỆ THÔNG TIN
____***____
BÀI TẬP
KỸ THUẬT SỐ ỨNG DỤNG
ĐỀ TÀI 16:
THIẾT KẾ MẠCH CHUYỂN MÃ
TỪ BCD 7421 SANG DƯ 3

Giảng viên : TS.Đặng Bá Lư
Sinh viên : Hồ Tá Quý
MSSV : 102130036
Lớp : 13T1
Đà Nẵng, ngày 11 tháng 11 năm 2015
Bài tập kĩ thuật số ứng dụng Thiết kế mạch chuyển mã BCD 7421 sang Dư 3
SVTH: HỒ TÁ QUÝ - LỚP 13T1
TRANG 2
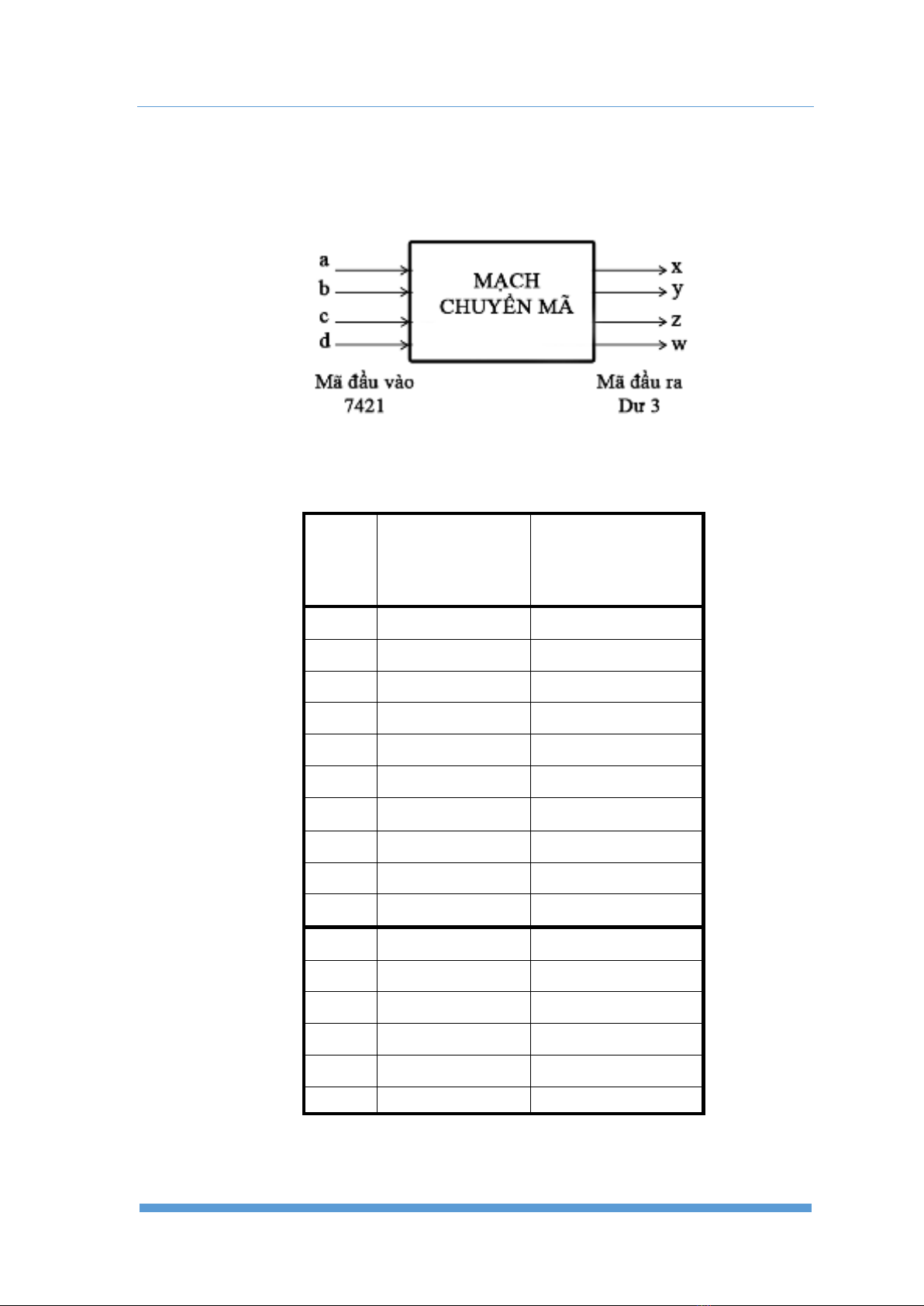
I. Mạch chuyển mã BCD 7421 sang Dư 3
II. Lập bảng công tác:
BCD 7421
ABCD
DƯ 3
XYZW
0
0000
0011
1
0001
0100
2
0010
0101
3
0011
0110
4
0100
0111
5
0101
1000
6
0110
1001
7
1000
1010
8
1001
1011
9
1010
1100
10
0111
xxxx
11
1011
xxxx
12
1100
xxxx
13
1101
xxxx
14
1110
xxxx
15
1111
xxxx
Bài tập kĩ thuật số ứng dụng Thiết kế mạch chuyển mã BCD 7421 sang Dư 3
SVTH: HỒ TÁ QUÝ - LỚP 13T1
TRANG 3
III. Thiết kế mạch dạng OR_AND, NAND_NAND
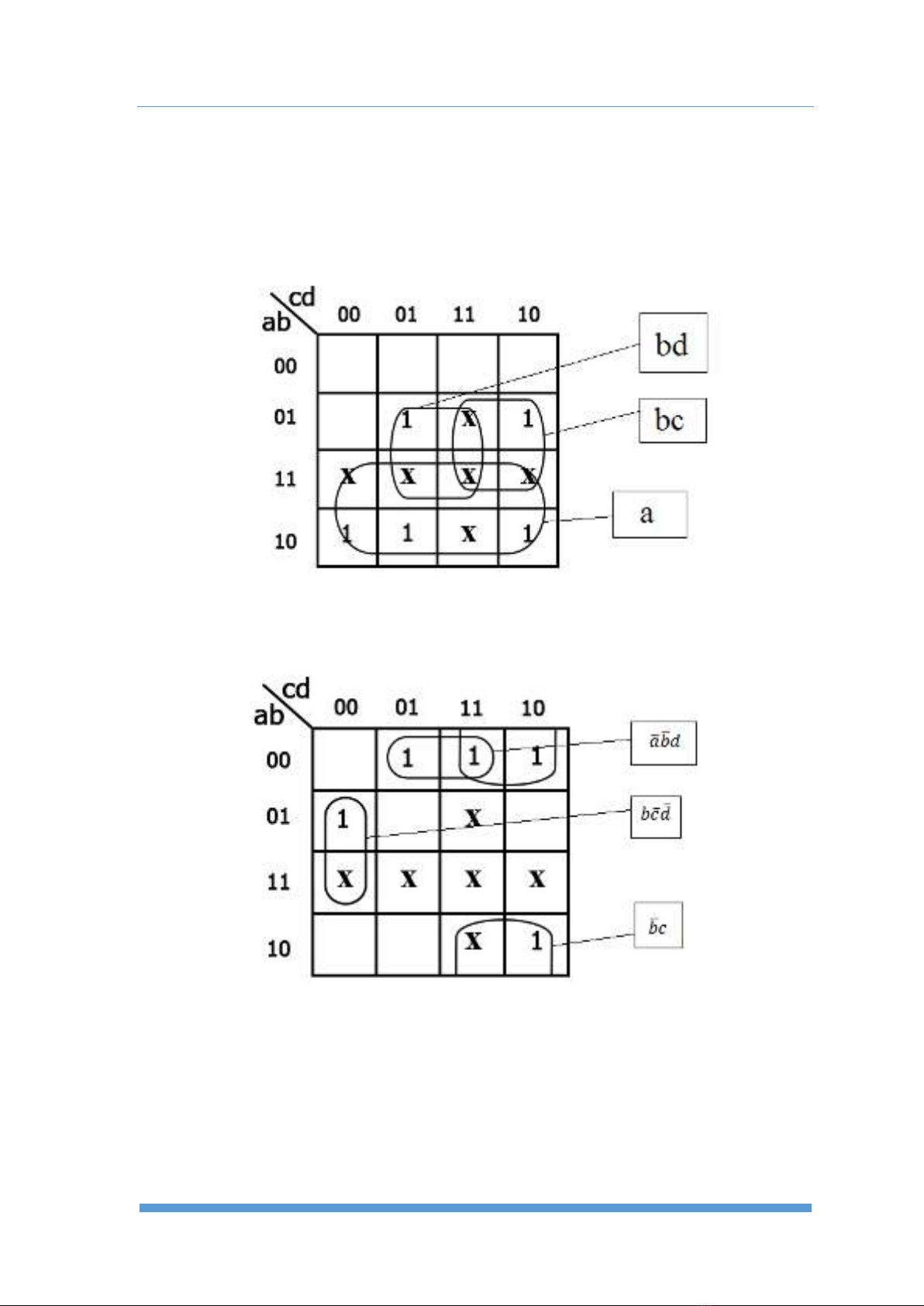
1. Tối giản bằng bảng K
- Đánh vòng các ô toàn 1 ta có biểu thức tối giản của nguyên hàm
Dựa vào bảng K ta có 𝑥(𝑎, 𝑏, 𝑐, 𝑑)= 𝑎 + 𝑏𝑑 +𝑏𝑐
Ta có 𝑦(𝑥, 𝑏, 𝑐, 𝑑)= 𝑏𝑐𝑑+ 𝑎𝑏
𝑑 + 𝑏
𝑐
Bài tập kĩ thuật số ứng dụng Thiết kế mạch chuyển mã BCD 7421 sang Dư 3
SVTH: HỒ TÁ QUÝ - LỚP 13T1
TRANG 4
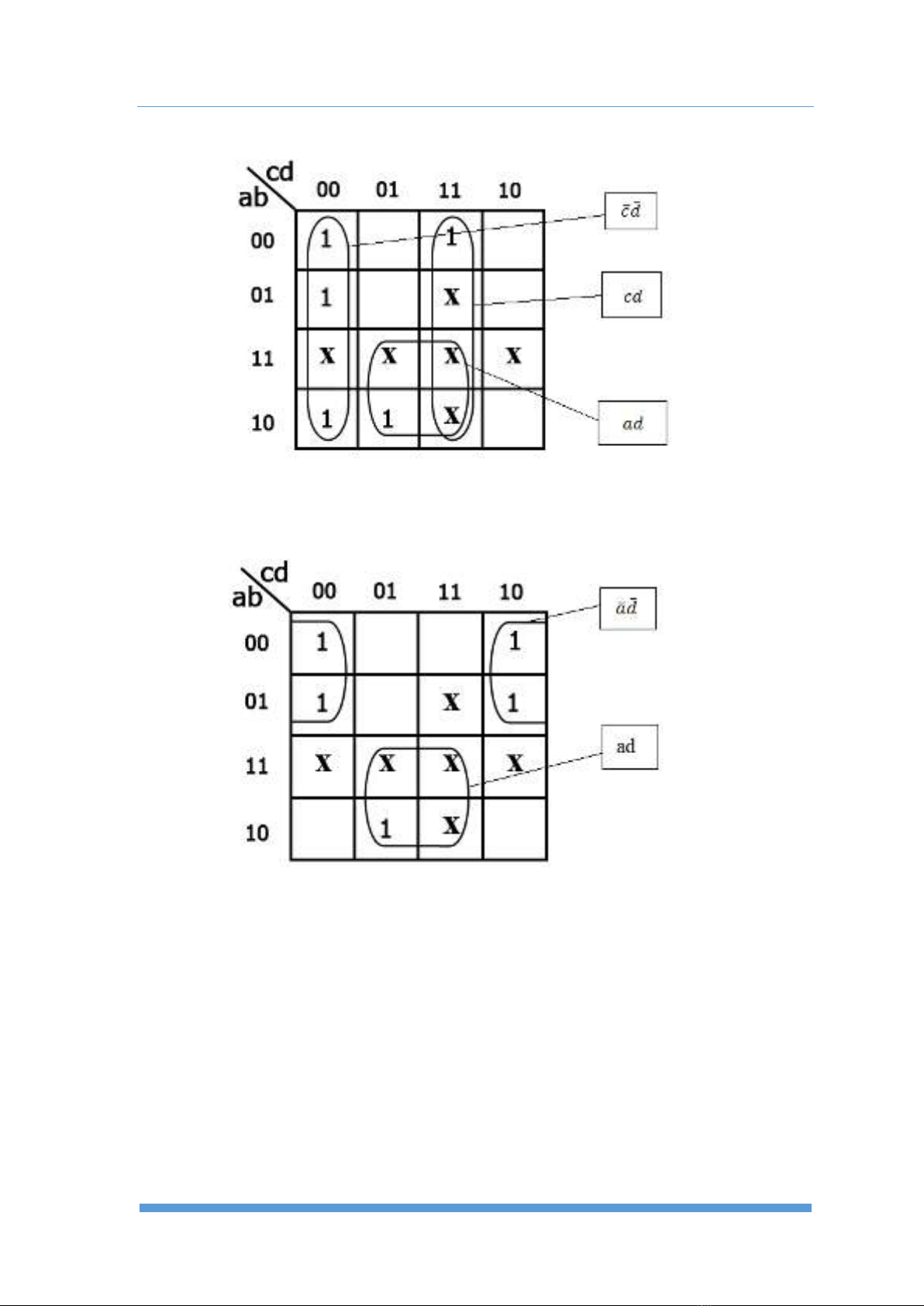
Ta có: 𝑧(𝑎, 𝑏, 𝑐, 𝑑)= 𝑐𝑑+𝑐𝑑 +𝑎𝑑
Ta có: 𝑤(𝑎, 𝑏, 𝑐, 𝑑)= 𝑎𝑑+𝑎𝑑
2. Tối giản bằng định lí logic.
a) x=∑(5,6,8,9,10) và điều kiện ràng buộc ∑(7,11,12,13,14,15)= 0
((𝑎𝑏
𝑐𝑑+𝑎𝑏𝑐𝑑)+(𝑎𝑏
𝑐𝑑+𝑎𝑏𝑐𝑑)+(𝑎𝑏
𝑐𝑑 + 𝑎𝑏𝑐𝑑)+(𝑎𝑏
𝑐𝑑+ 𝑎𝑏𝑐𝑑))
+(((𝑎𝑏𝑐𝑑+𝑎𝑏𝑐𝑑) + (𝑎𝑏𝑐𝑑 + 𝑎𝑏𝑐𝑑))+((𝑎𝑏𝑐𝑑 + 𝑎𝑏𝑐𝑑) + (𝑎𝑏𝑐𝑑+
𝑎𝑏𝑐𝑑)))
=( 𝑎𝑐𝑑+ 𝑎𝑐𝑑 + 𝑎𝑐𝑑 + 𝑎𝑐𝑑) + (𝑏𝑐𝑑 + 𝑏𝑐𝑑)+(𝑏𝑐𝑑 + 𝑏𝑐𝑑)
= a+bd+bc
Bài tập kĩ thuật số ứng dụng Thiết kế mạch chuyển mã BCD 7421 sang Dư 3
SVTH: HỒ TÁ QUÝ - LỚP 13T1
TRANG 5
b) y=∑(1,2,3,4,10) và điều kiện ràng buộc ∑(7,11,12,13,14,15)= 0
(𝑎𝑏
𝑐𝑑 + 𝑎𝑏
𝑐𝑑) + (𝑎𝑏
𝑐𝑑+𝑎𝑏
𝑐𝑑 + 𝑎𝑏
𝑐𝑑+ 𝑎𝑏
𝑐𝑑)+(𝑎𝑏𝑐𝑑+𝑎𝑏𝑐𝑑)
=(𝑎𝑏
𝑑 + 𝑏
𝑐 + 𝑏𝑐𝑑)
c) z=∑(0,3,4,8,9) và điều kiện ràng buộc ∑(7,11,12,13,14,15)= 0
(𝑎𝑏
𝑐𝑑+ 𝑎𝑏𝑐𝑑+ 𝑎𝑏
𝑐𝑑+a𝑏𝑐𝑑)+( 𝑎𝑏
𝑐𝑑 +
𝑎𝑏𝑐𝑑+𝑎𝑏
𝑐𝑑+ 𝑎𝑏𝑐𝑑)+(𝑎𝑏
𝑐𝑑 + 𝑎𝑏
𝑐𝑑 +𝑎𝑏𝑐𝑑+ 𝑎𝑏𝑐𝑑)
=𝑐𝑑+𝑐𝑑 +𝑎𝑑
d) w=∑0,2,4,6,9 và điều kiện ràng buộc ∑(7,11,12,13,14,15)= 0
((𝑎𝑏
𝑐𝑑+ 𝑎𝑏𝑐𝑑) + (𝑎𝑏
𝑐𝑑+ 𝑎𝑏𝑐𝑑)) + ((𝑎𝑏
𝑐𝑑 + 𝑎𝑏
𝑐𝑑) + (𝑎𝑏𝑐𝑑 +
𝑎𝑏𝑐𝑑))
= (𝑎𝑐𝑑+ 𝑎𝑐𝑑) + (𝑎𝑏
𝑑 + 𝑎𝑏𝑑)
= 𝑎𝑑+ad
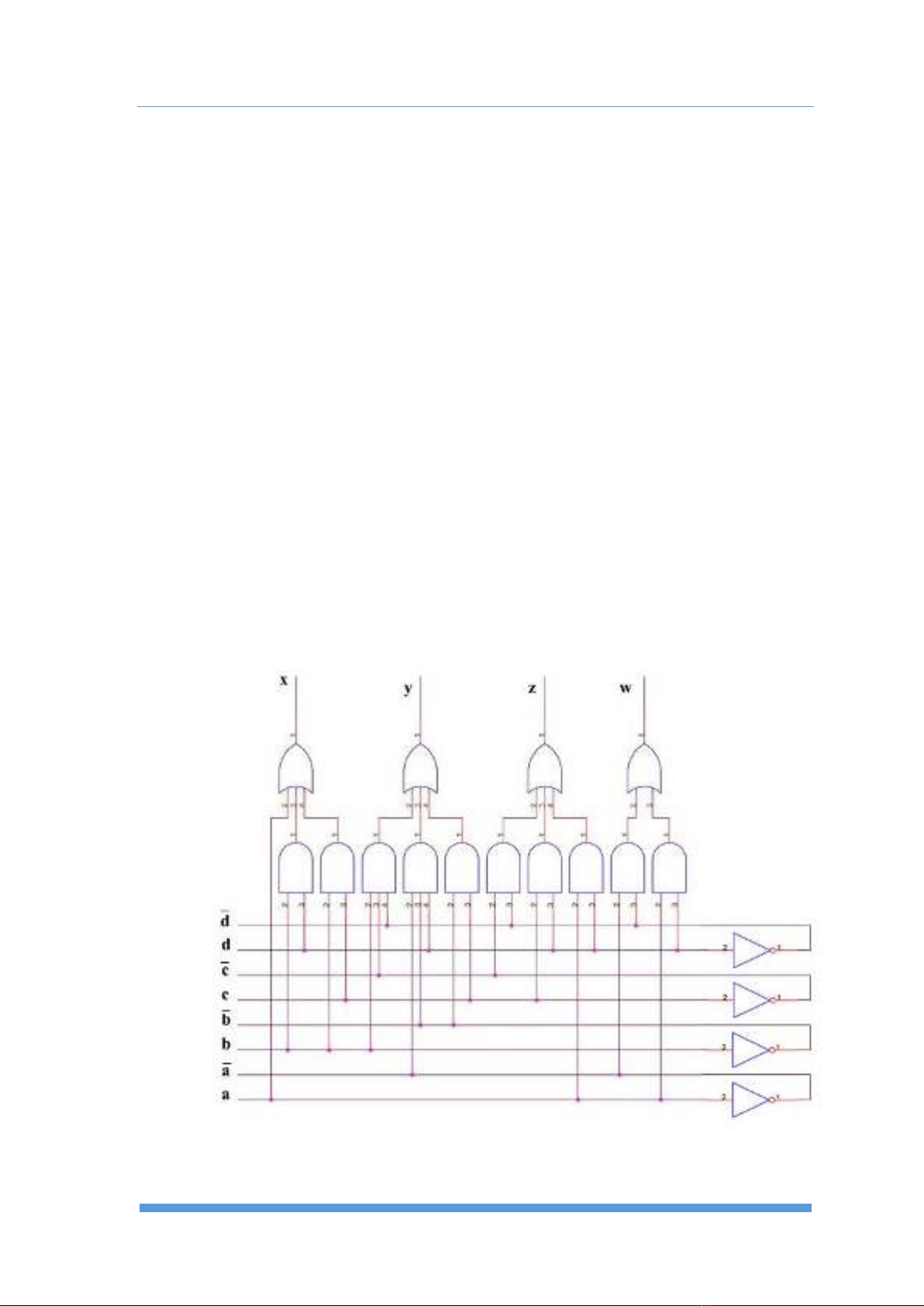
3. Thiết kế mạch.
a. Mạch OR_AND
𝑥(𝑎, 𝑏, 𝑐, 𝑑)= 𝑎 + 𝑏𝑑 +𝑏𝑐
𝑦(𝑥, 𝑏, 𝑐, 𝑑)= 𝑏𝑐𝑑+ 𝑎𝑏
𝑑 + 𝑏
𝑐
𝑧(𝑎, 𝑏, 𝑐, 𝑑)= 𝑐𝑑+𝑐𝑑 +𝑎𝑑
𝑤(𝑎, 𝑏, 𝑐, 𝑑)= 𝑎𝑑+𝑎𝑑
Vẽ mạch: