Bµi tËp lín c¬ kÕt cÊu 2 Tr- êng §¹i häc Má §Þa ChÊt
Sv:NguyÔn v¨n Tuyªn - 1 - Líp XDCTN
&
Má
Bài tập lớn số 2
TÝnh khung siªu tÜnh b»ng ph-¬ng ph¸p lùc
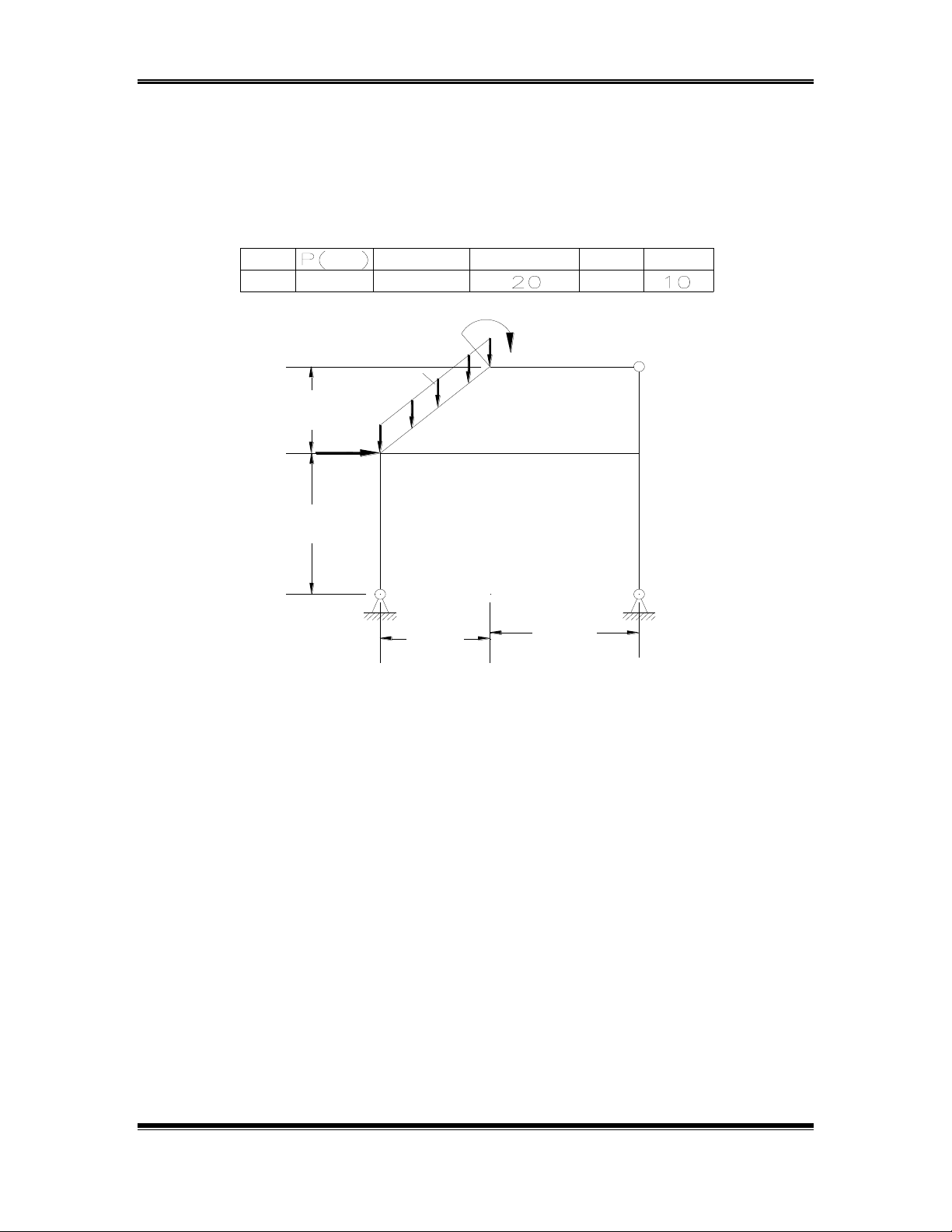
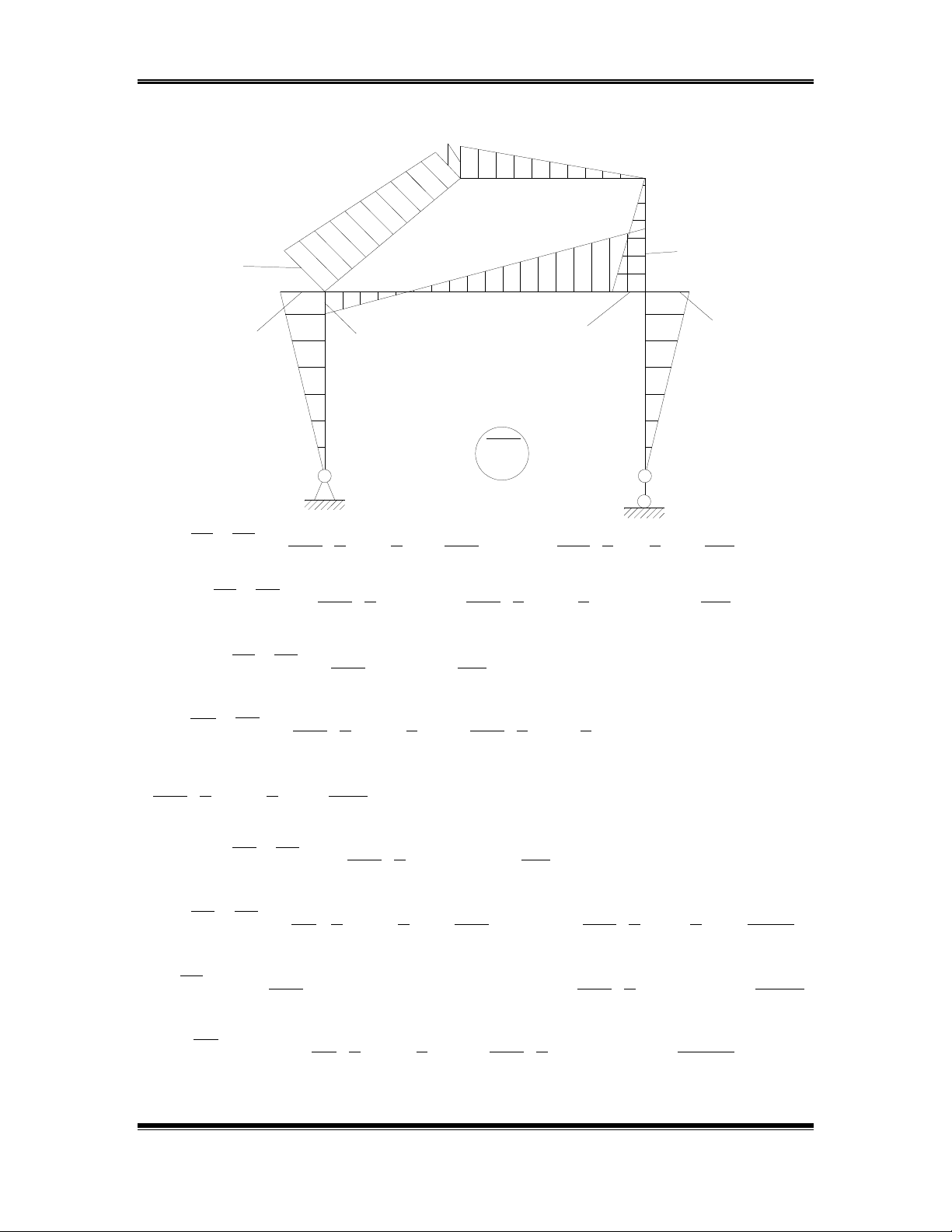
Bảng số liệu chung về kÝch th-íc vµ t¶i träng vµ s¬ ®å
B¶ng sè liÖu dÇm sè 5
stt knM(kNm) q(kN/m) L1(m)L2(m)
10
100
80
8
q
p
m
2J
2J
h
d
J
K2j
3J
3J
10(m)
8(m) 10(m)
6(m)
yªu cÇu vµ tù thùc hiÖn
1.tính hệ siêu tĩnh do tải trọng tác dụng
1.1,vẽ các biểu đồ nội lực:mômen uốn M
P
lực cắt Q
P
lực dọc N
P
trên hệ siêu tĩnh đã
cho.biết F=10J/L
2
1
(m
2
)
1) x¸c ®Þnh bËc siªu tÜnh vµ chän hÖ c¬ b¶n
2)thµnh lËp c¸c ph- ¬ng tr×nh d¹ng chÝnh t¾c d¹ng tæng qu¸t
3)x¸c ®Þnh c¸c hÖ vµ sè h¹ng tù do cña ph- ¬ng tr×nh chÝnh t¾c,kiÓm tra c¸c kÕt
qu¶ tÝnh ®- îc.
4)gi¶i hÖ ph- ¬ng tr×nh chÝnh t¾c
5)vÏ biÓu ®å m«men trªn hÖ siªu tÜnh ®· cho do t¶i träng t¸c dông M
P
.kiÓm tra
c©n b»ng c¸c nót vµ ®iÒu kiÖn chuyÓn vÞ.
6)vÏ biÓu ®å lùc c¾t Q
P
vµ lùc däc N
P
trªn hÖ siªu tÜnh ®· cho
1.2.x¸c ®Þnh chuyÓn vÞ ngang cña 1 ®iÓm hoÆc gãc soay cña tiÕt diÖn K biÕt
E=2.10
8
kN/m
2
.J=10
6
L
4
1
(m
4
)
2.tÝnh hÖ siªu tÜnh t¸c dông c¶ 3 nguyªn nh©n(t¶i träng,nhiÖt ®é thay ®æi vµ gèi tùa
dêi chæ).
2.1 viÕt hÖ ph- ¬ng tr×nh chÝnh t¾c d¹ng sè
2.2 tr×nh bµy
Bµi tËp lín c¬ kÕt cÊu 2 Tr- êng §¹i häc Má §Þa ChÊt
Sv:NguyÔn v¨n Tuyªn - 2 - Líp XDCTN
&
Má
1)c¸ch vÏ biÓu ®å M
cc
do 3 nguyªn nh©n ®ång thêi t¸c dông lªn hÖ siªu
tÜnh ®· cho vµ c¸ch kiÓm tra
2)c¸ch tÝnh chuyÓn vÞ ®· nªu môc trªn
BiÕt
-nhiÖt ®é thay ®æi trong thanh xiªn : thí trªn T
tr
=+36
0
,thí d- íi lµ T
d
=+28
0
-tÝnh thanh xiªn cã chiÒu cao tiÕt diÖn h=0.1(m)
HÖ sè gi¶n në dµi v× nhiÖt ®é
=10
5
-chuyÓn vÞ gèi tùa
Gèi D dÞch chuyÓn sang ph¶i mét ®o¹n
1
=0.001 L
1
(m)
Gèi H bÞ lón xuèng mét ®o¹n
2
=0.001 L
2
(m)
Bµi lµm
Thứ tự thực hiện:
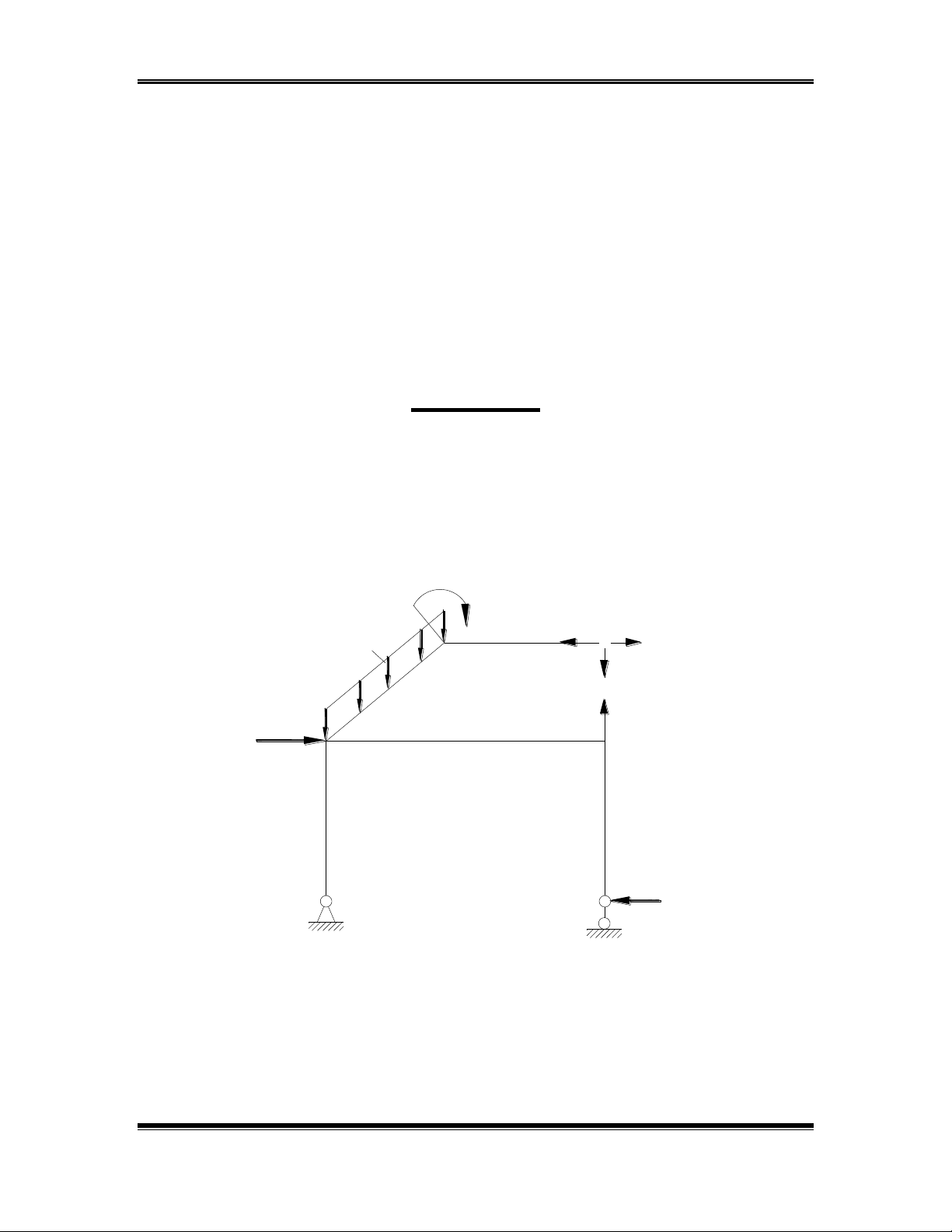
1. Xác định số ẩn số, chọn hệ cơ bản và lập hệ phương trình chính tắc dưới dạng chữ:
Số ẩn số: n=T+2K+C
0
+3H-3D =3
với (K=1,H=5,C
0
=4,D=6,T=0)vậy số bậc siêu tĩnh bằng 3
Hệ cơ bản chọn như h×nh d- íi ®©y:
X3 = 1
X2 = 1
X1 = 1
CHäN HÖ C¥ B¶N
m
p
q
Bµi tËp lín c¬ kÕt cÊu 2 Tr- êng §¹i häc Má §Þa ChÊt
Sv:NguyÔn v¨n Tuyªn - 3 - Líp XDCTN
&
Má
Hệ phương trình chính tắc d¹ng tæng qu¸t ®- îc thµnh lËp
11X1 + 12X2 + 13X3 + 1P = 0
21X1 + 22X2 + 23X3 + 2P = 0
31X1 + 32X2 + 33X3 + 3P = 0
2. Xác định các hệ số và số hạng tự do của hệ phương trình chính tắc:
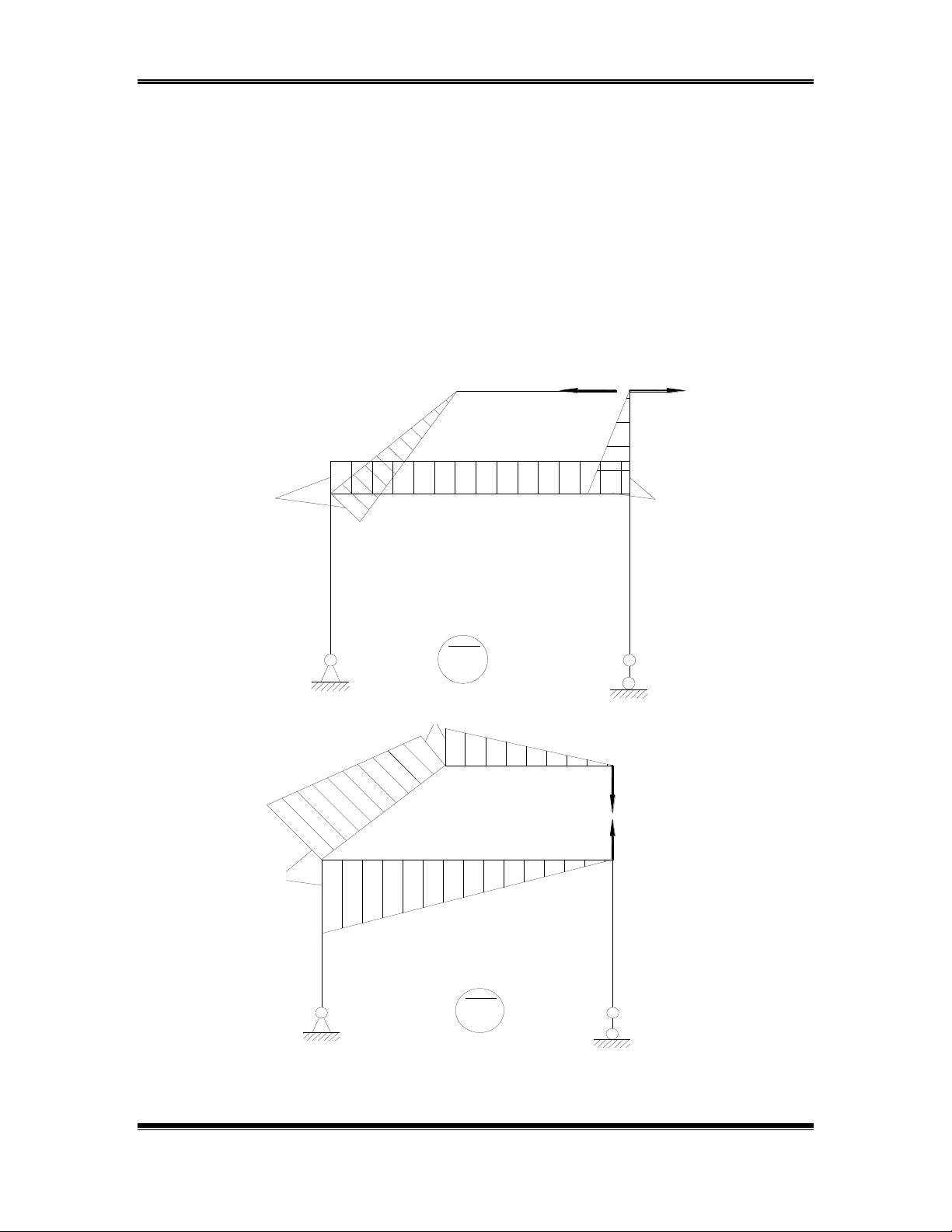
Các biểu đồ mômen uốn lần lượt do X1 = 1; X2 = 1; X3 = 1 và tải trọng gây ra
trong hệ cơ bản như trên:
M 1
66
X 1 = 1
18
10
M 2
X 2 = 1
Bµi tËp lín c¬ kÕt cÊu 2 Tr- êng §¹i häc Má §Þa ChÊt
Sv:NguyÔn v¨n Tuyªn - 4 - Líp XDCTN
&
Má
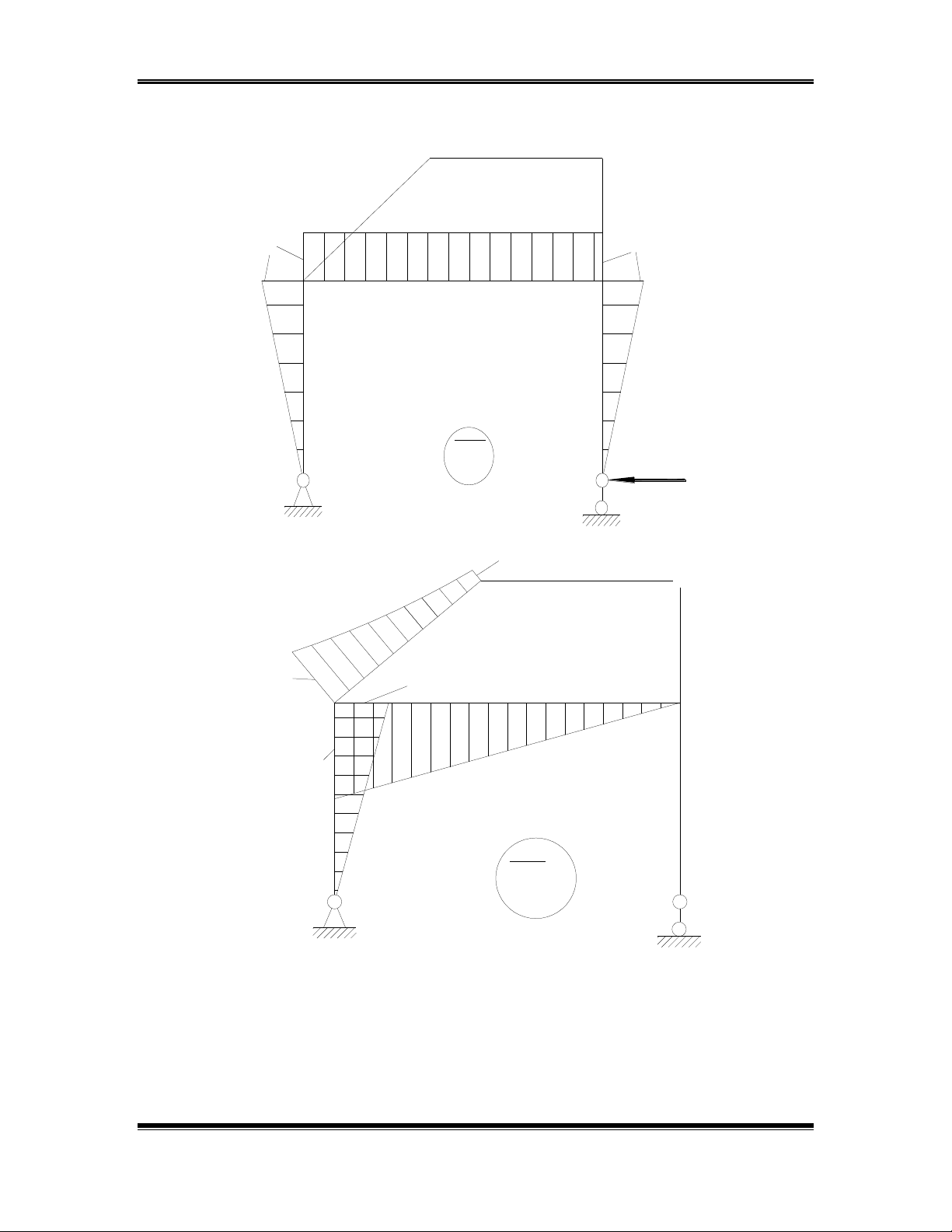
X3 = 1
M 3
10
10
M 0 p
1700
800
100
900
Bµi tËp lín c¬ kÕt cÊu 2 Tr- êng §¹i häc Má §Þa ChÊt
Sv:NguyÔn v¨n Tuyªn - 5 - Líp XDCTN
&
Má
10 10
Ms
2
16
6
12
10
11 = (
1
M
)(
1
M
) =
EJEJEJEJ
408
6.
3
2
.6.6.
2
1
3
1
6.18.6
2
1
6.
3
2
.10.6.
2
1
2
1
12=21=(
1
M
)(
2
M
)=
108.
3
2
10.6
2
1
2
1
6.18.18.
2
1
2
1
EJEJ
EJ
716
13 = 31 = (
1
M
)(
3
M
) =
.6.18.10
2
1
EJ
EJ
540
22 = (
2
M
)(
2
M
) =
14.10.10108.
3
2
.10.8.
2
1
2
1
18.
3
2
.18.18.
2
1
2
1
EJEJ
+
10.
3
2
.10.10.
2
1
2
1
EJ
=
EJ3
6436
23 = 32 = (
2
M
)(
3
M
) =
10.18.18.
2
1
2
1
EJ
EJ
810
33 = (
3
M
)(
3
M
) =
10
3
2
.10.10.
2
1
.
1
EJ
+
10.18.10
2
1
EJ
+
10
3
2
.10.10
2
1
3
1
EJ
=
EJ9
12100
1P=(
1
M
)(
o
P
M
)=
dZZZZ
EJ )6.0).(9001608(
2
110
0
2
6.18.1700.
2
1
2
1
EJ
=
EJ
49400
3P = (
3
M
)(
o
P
M
) =
10.18.1700.
2
1
2
1
800.
3
2
.10.10.
2
11
EJEJ
=
EJ3
309500