Bài tập vật lý nguyên tử hạt nhân
PHẦN VẬT LÝ NGUYÊN TỬ
CÁC MẪU NGUYÊN TỬ THEO LÝ THUYẾT CỔ ĐIỂN
BÀI 1. MẪU NGUYÊN TỬ RUTHERFORD
1. 1) a) Sau khi xuyên qua một lá vàng, một hạt với năng lượng E = 4MeV bị tán xạ dưới một
góc = 10o. Hãy tính khoảng nhằm b của nó. Cho biết nguyên tử số của vàng Z=79.
b) Tìm xung lượng (động lượng) và động năng mà truyCn cho hạt nhân vàng do sD tán xạ
gây ra
1. 2) Tính khoảng cách cDc tiểu khi một hạt có động năng T = 0,4 MeV (khoảng nhằm b=0) đến
gần:
a) Một hạt nhân nguyên tử chì nặng đứng nghỉ.
b) Một hạt nhân 7Li nhẹ, tD do, lúc đầu đứng nghỉ.(Cho biết khối lượng hạt nhân nguyên tử
He (hạt ) m
= 6,644.10-24g và khối lượng hạt nhân nguyên tử Li mLi=11,519.10-24g).
1. 3) Một chùm hạt hẹp có động năng T = 0.5 MeV đập vuông góc lên một lá vàng(A=197g/mol,
Z=79) có mật độ khối lượng theo diện tích d = 1.5 mg/cm2. Cường độ của chùm hạt là I0 =
5.105 hạt/s. Tìm số hạt bị tán xạ bởi lá vàng sau = 30 phút trong các khoảng góc:
a) 590 – 610 .
b) Trên 600.
1. 4) Theo điện động lDc h\c c] điển, một Electron, chuyển động với gia tốc a s^ m_t năng lượng do
bức xạ sóng điện t` với tốc độ biến thiên năng lượng theo qui luật:
dE
dt =− 2e2
3c3a2
trong đó e là diện tích Electron, C là vận tốc ánh sáng. Để đbn giản ta xem gia tốc của Electron
luôn luôn trùng với gia tốc hướng tâm. Hãy tính thời gian để một Electron chuyển động theo
quc đạo tròn trong nguyên tử Hydro với bán kính r = 0,5Ao sau đó s^ rbi vào hạt nhân.
1. 5) Khi tiến hành thí nghiệm tán xạ hạt
α
lên hạt nhân đồng, Rbdepho nhận th_y rằng hạt
α
với
động năng 5MeV va chạm đàn hồi với hạt nhân đồng. Sau đó bị giật lùi ngược lại với động
năng 3,9MeV. Hãy xác định tỷ lệ giữa khối lượng hạt nhân đồng và hạt
α
.
BÀI 2. MẪU NGUYÊN TỬ BOHR
1. 6) Một hạt có khối lượng m chuyển động theo một quỹ đạo tròn trong một trường thế đối xứng
xuyên tâm U(r)=kr2/2. Bằng điCu kiện lượng tử của Bohr, hãy tìm các bán kính có thể có của
quỹ đạo và các mức năng lượng của hạt này.
1. 7) Sử dụng lý thuyết Bohr, hãy xác định bán kính a0 quỹ đạo thứ nh_t của electron và vận tốc v0
của nó trên quỹ đạo này.
1. 8) Tính cường độ điện trường của hạt nhân ở quỹ đạo Bohr thứ 2 và thứ 5.
1. 9) Các vạch ph] nào s^ xu_t hiện khi kích thích nguyên tử Hidro bằng các phôtôn năng lượng
12.5eV.
1. 10) Tìm giới hạn vùng ph] trong đó có các vạch dãy Balmer của nguyên tử Hidro.
1. 11) Nguyên tử Hidro ban đầu đứng yên phát ra photon với tần số tưbng ứng với vạch đầu của dãy
Lyman. Hãy tìm vận tốc của nguyên tử sau khi phát photon.
1. 12) Xác định năng lượng nhỏ nh_t cần truyCn cho nguyên tử Berili ion hoá 3 lần ở trạng thái cb
bản để kích thích quang ph] toàn phần của nguyên tử này.
1. 13) Tính năng lượng cần truyCn cho nguyên tử Hidro để dãy Balmer của nó chỉ có một vạch ph].
Trang 1
Bài tập vật lý nguyên tử hạt nhân
1. 14) Tính hiệu số bước sóng của các vạch H (vạch đầu tiên của dãy Balmer) đối với Hidro và
Triti, biết rằng bước sóng của vạch H của Hidro bằng 6563 A0 và khối lượng hạt nhân Triti
g_p 3 lần khối lượng hạt nhân Hidro.
1. 15) Tìm tỉ số giữa các hằng số Ritbec đối với hidro và heli nếu như khối lượng của hạt nhân
nguyên tử hidro là mH = 1,672.10-24g, của hạt nhân nguyên tử heli mHe = 6,644.10-24g và của
eletron là me = 9,1.10-28g.
1. 16) Trong thí nghiệm kiểm chứng các định đC N.Bohr khi dùng electron bpn vào nguyên tử
Hydro để kích thích nó, người ta đo được các giá trị hiệu điện thế kích thích là 10,2v và 12,1V
và có 3 vạch quang ph]. Hãy tính bước sóng của các vạch quang ph] _y và xác định những
vạch quang ph] _y thuộc những dãy nào?
Trang 2
Bài tập vật lý nguyên tử hạt nhân
CƠ SỞ CỦA THUYẾT LƯỢNG TỬ
BÀI 1. LÝ THUYẾT PHOTON
2. 1) Tìm năng lượng và xung lượng của một photon có bước sóng 10 A0.
2. 2) Thiết lập hệ thức năng – xung lượng tưbng đối tính của một hạt. T` đó suy ra đối với photon,
hệ thức năng xung lượng tưbng đối tính có dạng .
2. 3) Hãy xác định tần số của một photon sinh ra khi một electron có năng lượng 30keV bị d`ng lại
sau một va chạm duy nh_t vào hạt nhân nặng. Xung lượng của hệ có được bảo toàn không?
2. 4) Chứng minh rằng, electron tD do không thể phát ra lượng tử ánh sáng (photon), vì nếu giả
sử electron phát ra lượng tử ánh sáng thì thì s^ không thoả mãn đồng thời các định luật bảo
toàn năng lượng và xung lượng.
2. 5) Hãy xác định năng lượng, xung lượng và khối lượng của photon ánh sáng có bước sóng
λ=600 A0
.
BÀI 2. HIỆU ỨNG COMPTON
2. 6) Chứng tỏ rằng khi một photon có năng lượng E tán xạ trên một electron tD do thì động năng
giật lùi cDc đại của electron được cho bởi:
Kmax =E2
E+mc2/2
m: khối lượng nghỉ của electron.
2. 7) Bước sóng phải tăng bao nhiêu phần trăm để cho một photon khi va chạm Compton với
electron tD do m_t 78% năng lượng của nó.
2. 8) Chứng tỏ rằng
ΔE
E
- độ m_t mát năng lượng tỷ đối – của photon trong va chạm Compton được
cho bởi công thức:
2. 9) Một photon tia X có năng lượng 6.2KeV đập vào một khối Cacbon bị tán xạ bởi va chạm
Compton và tần số của nó bị dịch đi 0.01%.
a) Photon đó bị tán xạ ở góc nào?
b) Động năng được truyCn cho electron là bao nhiêu?
BÀI 3. SÓNG DE BROGLIE
2. 10) Một viên đạn có khối lượng 40g bay với vận tốc 100m/s.
a) Chúng ta có thể gán cho nó bước sóng bằng bao nhiêu?
b) Tại sao bản ch_t sóng của viên đạn không tD bộc lộ qua hiệu ứng nhiễu xạ?
2. 11) 2. Khi tăng năng lượng của electron thêm 200ev thì bước sóng DbBrbi của nó thay đ]i hai
lần. Hãy tính bước sóng lúc ban đầu.
2. 12) Tìm bước sóng De Broglie cho các trường hợp sau:
a) Êlectron chuyển động có động năng 10eV.
b) Êlectron chuyển động có động năng 1MeV.
c) Một quả bóng khối lượng 45g chuyển động với vận tốc 2m/s.
So sánh các kết quả thu được.
2. 13) Bpt đầu t` giá trị nào của động năng của các electron thì sai số vC bước sóng de Broglie trong
quá trình tính toán theo c] điển s^ vào cỡ 10%?
Trang 3
pcE
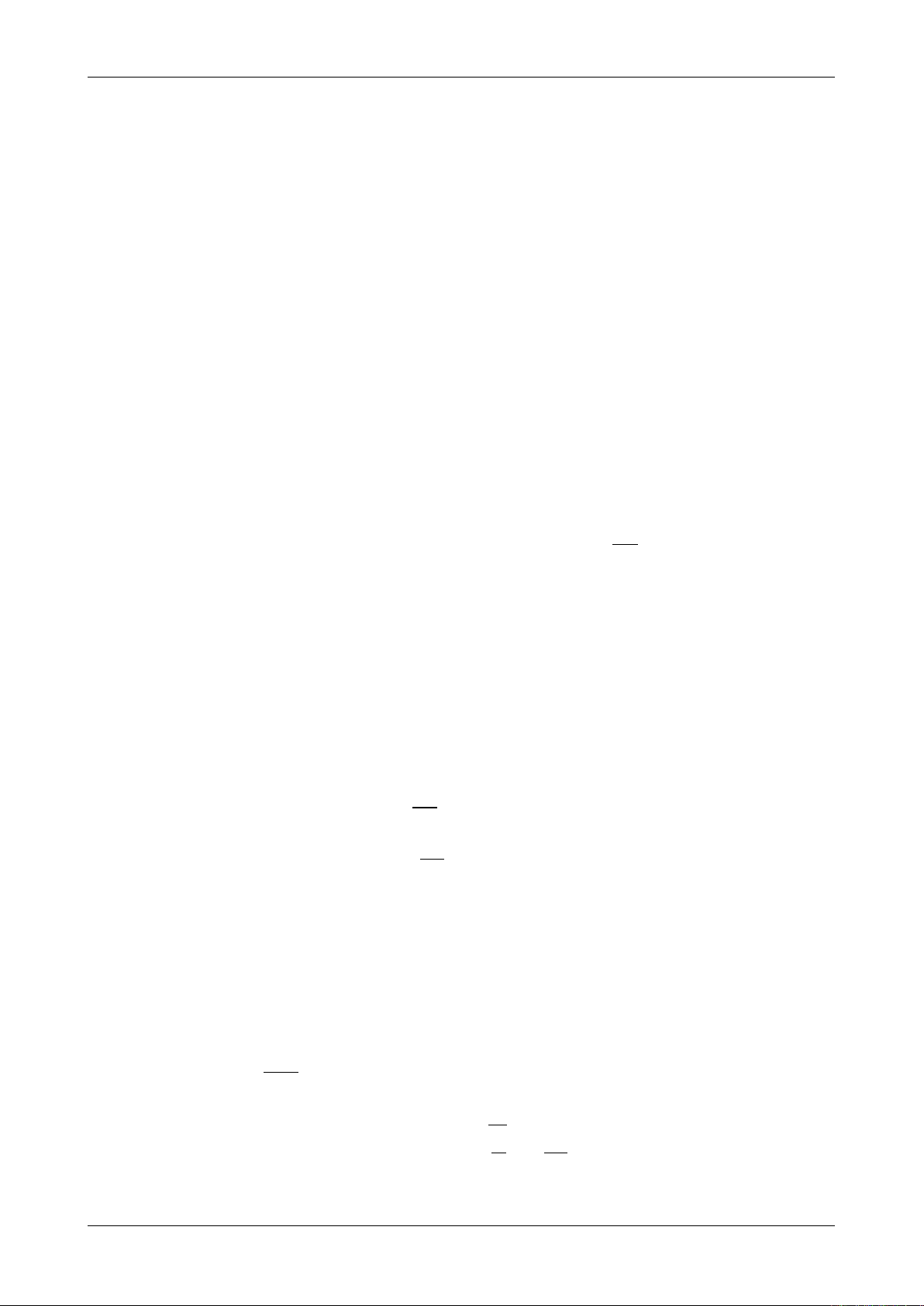
Bài tập vật lý nguyên tử hạt nhân
2. 14) Tính tỉ số giữa bước sóng Compton và bước sóng De Broglie của một hạt.
2. 15) Tính hiệu điện thế cần thiết để tăng tốc một êlectron chuyển động trong điện trường để có
bước sóng De Broglie bằng 1A0.
2. 16) Khi tính bước sóng de Broglie cho các hạt tưbng đối tính, ta phải biểu diễn xung lượng của
hạt qua động năng của nó theo công thức của thuyết tưbng đối. Hãy cho biết với giá trị động
năng bằng bao nhiêu so với giá trị năng lượng tcnh thì việc áp dụng công thức phi tưbng đối
tính để tính bước sóng de Broglie s^ phạm phải một sai số tỷ đối cho phép nhỏ hbn 1%.
2. 17) Một chùm nbtron nhiệt năng lượng 0,05eV nhiễu xạ trên đbn tinh thể muối ăn (NaCl). Xác
định góc trượt
θ
ứng với bậc nhiễu xạ thứ nh_t (n = 1) theo điCu kiện Vunphb – Brpc:
2dsinθ=nλ
. Cho biết hằng số mạng tinh thể là d = 2,81A0.
BÀI 4. HỆ THỨC BẤT ĐỊNH HEISENBERG
2. 18) Giả sử có thể đo được xung lượng của một hạt chính xác đến phần nghìn. Xác định độ b_t
định cDc tiểu vC vị trí của hạt:
a) Nếu hạt có khối lượng 5mg và vận tốc 2m/s.
b) Nếu hạt là Electron có vận tốc 1,8.106 m/s.
2. 19) Chứng minh rằng đối với 1 hạt mà độ b_t định vC vị trí là
Δx=λ
2π
, trong đó
λ
là bước sóng
De Broglie của hạt thì độ b_t định cDc tiểu vC vận tốc bằng một lượng có độ lớn cùng bậc với
chính vận tốc của hạt.
2. 20) Độ rộng của một vạch quang ph] ứng với bước sóng 4000A0 bằng 10-4 A0. Tính thời gian
trung bình để hệ nguyên tử tồn tại ở trạng thái năng lượng tưbng ứng.
2. 21) DDa vào hệ thức b_t định ước lượng động năng cDc tiểu của một electron chuyển động trong
một miCn có kích thước l ~0,1nm.
2. 22) Giả sử xét một êlectron bị l\t vào khoảng trống của một mạng tinh thể sao cho chuyển động
của nó chỉ giới hạn trong một thể tích hình cầu có bán kính 2A0. Hãy đánh giá năng lượng cDc
tiểu mà êlectron có thể có trong điCu kiện trên.
2. 23) Sử dụng hệ thức b_t định
Δx .Δpx≥h
2π
để chứng minh rằng khi một hạt chuyển động theo
quỹ đạo tròn thì ta cũng có
ΔL .Δθ≥h
2π
. Các đại lượng
ΔL
và
Δθ
là các độ b_t định vC
moment động lượng và góc quay.
2. 24) Động năng của êlectron trong nguyên tử Hydro có giá trị bằng 10eV. Một cách gần đúng có
thể dùng hệ thức b_t định để xác định kích thước nhỏ nh_t của nguyên tử.
BÀI 5. HÀM SÓNG VÀ PHƯƠNG TRÌNH SCHRODINGER
2. 25) Hàm sóng của hạt bị nhốt trong một giếng thế vô hạn và ở trạng thái năng lượng th_p nh_t
được cho bởi hàm sóng:
ψ=Asin
(
πx /L
)
. Sử dụng điCu kiện chuẩn hoá hàm sóng, chứng
minh rằng:
A=
√
2/L
.
2. 26) Một hạt bị nhốt giữa hai bức tường rpn cách nhau khoảng L. Biết rằng hạt ở trong trạng thái
có năng lượng th_p nh_t và có hàm sóng:
ψ=
√
2
Lsin
(
πx
L
)
. Dùng hàm sóng này hãy tính xác
su_t để tìm th_y hạt giữa các điểm:
Trang 4
Bài tập vật lý nguyên tử hạt nhân
a) x = 0 và x = L/3.
b) x = L/3 và x = 2L/3.
c) x = 2L/3 và x = L.
2. 27) Cũng bài toán trên nhưng hạt ở trong trạng thái kích thích với n = 3. Hỏi tại những điểm nào
trong khoảng 0 < x < L, mật độ xác su_t tìm th_y hạt có giá trị cDc trị.
2. 28) Hàm sóng của dao động tử điCu hoà một chiCu khối lượng m ở trạng thái cb bản có dạng:
ψ
(
x
)
=Ae−αx2
Trong đó A là hệ số chuẩn hoá, là hằng số dưbng. Sử dụng phưbng trình Schrodinger để
tính và tìm năng lượng tưbng ứng với trạng thái đó của dao động tử điCu hoà.
2. 29) Hạt ở trong giếng thế năng một chiCu, cao vô cùng
U
(
x
)
=¿
{
0 0<x<a¿¿¿¿
a) Hạt ở trạng thái ứng với n = 2. Xác định những vị trí ứng với cDc đại và cDc tiểu của mật
độ xác su_t tìm th_y hạt.
b) Hạt ở trạng thái n = 2. Tính xác su_t để tìm hạt có vị trí trong khoảng
a
3≤x≤2a
3
.
c) Tìm vị trí x tại đó xác su_t tìm th_y hạt ở các trạng thái n = 1 và n = 2 là như nhau.
Trang 5