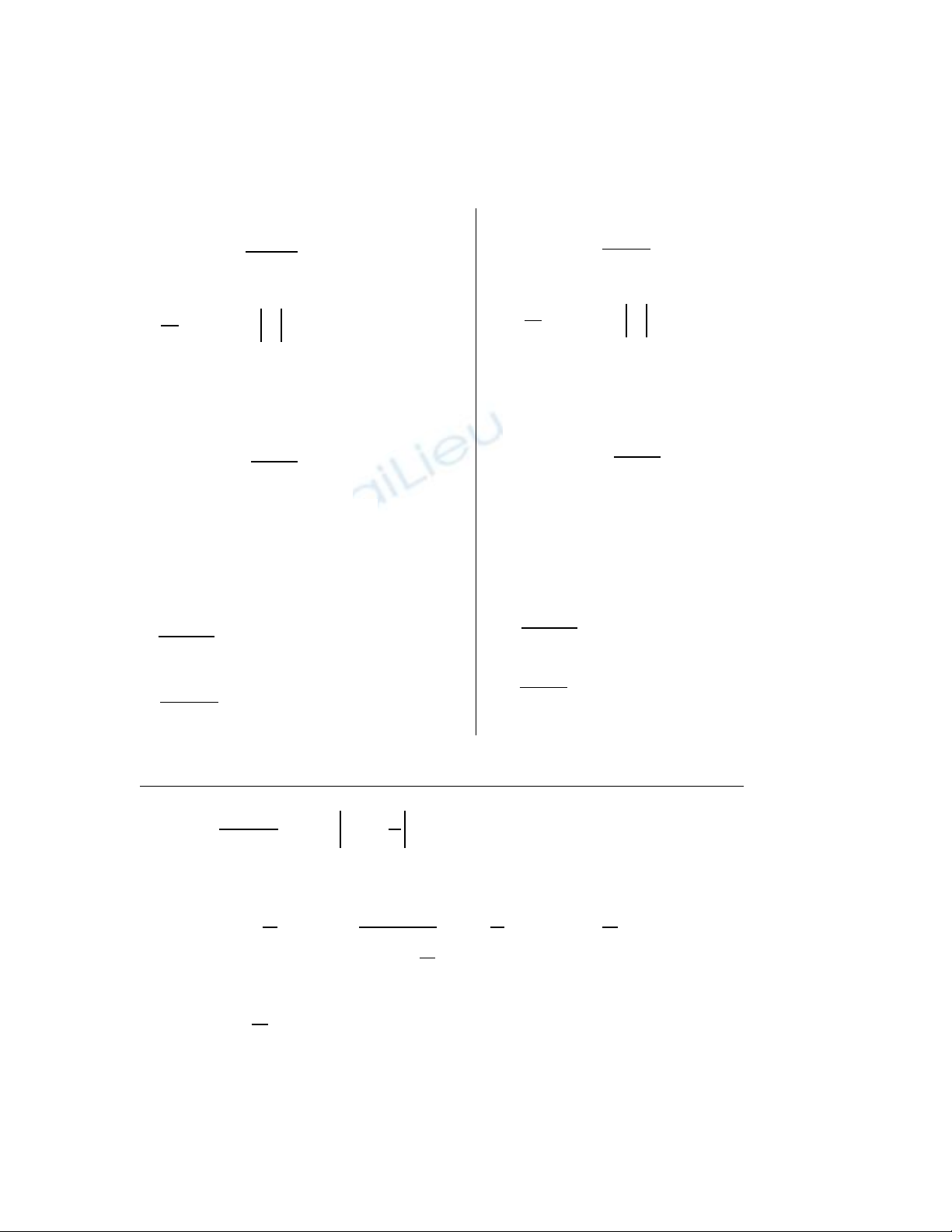
B ng các tích phân c b nả ơ ả
đây ch vi t cho hàm y = f(x) còn hàm y = f(u) làm t ng tở ỉ ế ươ ự
Hàm C BơnảHàm H pợ
1
1
n
n
x
x dx C
n
+
= +
+
+
( n
(
-1 )
1lndx x C
x
= +
=
x x
e dx e C
= +
=
ln
x
x
a
a dx C
a
= +
=
sin . osx dx c x C
= − +
=
os . sinc x dx x C
= +
=
2
tan
os
dx x C
c x
= +
=
1
1
n
n
u
u du C
n
+
= +
+
+
( n
(
-1 )
1lndu u C
u
= +
=
u u
e du e C
= +
=
ln
u
u
a
a du C
a
= +
=
sin . osu du c u C
= − +
=
os . sinc u du u C
= +
=
( )
2
2
1 t an tan
os
du u du x C
c u
= + = +
� �
( )
2
2
1 cot cot
sin
du u du x C
u
= − + = − +
� �
Nh ng công th c sau đây mu n s d ng ph i ch ng minh:ữ ứ ố ử ụ ả ứ
1.
2
ln tan
sin
x
dx C
x
= +
=
Ch ng minh:ư
Đ t ặ
2
2
1 1
tan . 1 tan
2 2 2
2 os 2
x x
t dt dx dx
x
c
� �
= = = +�� �
� �
( )
2
1. 1
2
dt t dx
= +
Ta có công th c l ng giác sau: ứ ượ
2 2 2
2
2sin . os 2 tan
22 2 2
sin , sin
1sin os 1 tan
2 2 2
x x x
c
t
x vi x
tx x x
c
� �
� �
� �
= = =
� �
+� � � � � �
+ +
� �
� � � � � �
� � � � � �
� �
( )
2
2
2
2
1ln ln tan
2
sin
1
x
dt
t
dx dt t C C
t
x t
t
+
= = = + = +
+
� � �
2.
( )
2 4
ln tan
os
x
dx C
c x
π
= + +
=
Ch ng minh:ứ
Ta có
os sin 2
c x x
π
� �
= +
� �
� �
Làm t ng t bài trên:ươ ự
Đ tặ
2
2
1 1
tan . 1 tan
2 4 2 2 4
2 os 2 4
x x
t dt dx dx
x
c
π π
π
� �
� � � �
= + = = + +�
� � � �
� �
� �
� � � �
� �
+
� �
� �
( )
2
1. 1
2
dt t dx
= +
( )
2
2
2
1ln ln tan
2
os 2 4
1
dt
t
dx dt x
t C C
t
c x t
t
π
+� �
= = = + = + +
� �
� �
+
� � �
3.
2 2
1ln
2a
dx a x C
a x a x
+
= +
− −
−
( a
(
0 )
Ch ng minh:ứ
( ) ( )
( )
2 2
1 1 1
2a
1 1
ln ln ln
2a 2a
dx dx
a x a x a x
a x
a x a x C
a x
� �
= −
� �
− + −
� �
+
� �
= + − − = +
� �
−
� �
� �
4.
2 2
1ln
2a
dx x a C
x a x a
−
= +
− +
−
( a
(
0 )
Ch ng minh:ứ
( ) ( )
( )
2 2
1 1 1
2a
1 1
ln ln ln
2a 2a
dx dx
x a x a x a
x a
x a x a C
x a
� �
= −
� �
− − +
� �
−
= − − + = +
+
� �
5 .
2 2
2 2
ln , 0
dx x x a C a
x a = + + +a
+
+
Ch ng minh:ứ
Đ t ặ
2 2
u x x a
= + +
2 2
2 2 2 2
1x x x a
du d dx
x a x a
� �
� � + +
= + = � �
� � � �
+ +
� � � �
2 2
du dx
ux a
=+
2 2
2 2
ln ln
dx du u x x a C
u
x a
= = = + + +�+
� �
6.
2 2
2 2
ln , 0
dx x x a C x a
x a
= + − + > >
−
−
Ch ng minh:ứ
Đ t ặ
2 2
u x x a
= + −
2 2
2 2 2 2
1x x x a
du d dx
x a x a
� �
� � + −
= + = � �
� � � �
+ −
� � � �
2 2
du dx
ux a
=−
2 2
2 2
ln ln
dx du u x x a C
u
x a
= = = + − +�−
� �
7.
2 2 2
ln
2 2
x A
x Adx x A x x A C
+ = + + + + +
+
Ch ng minh:ứ
Đ t ặ
2
2
, ,
x
u x A dv dx du v x
x A
= + = = =�+
2
2 2
2
x
x Adx x x A dx
x A
+ = + − +
� �
2
2
2
x A A
x x A dx
x A
+ −
= + − +
+
2 2
2
dx
x x A x Adx A
x A
= + − + + +
� �
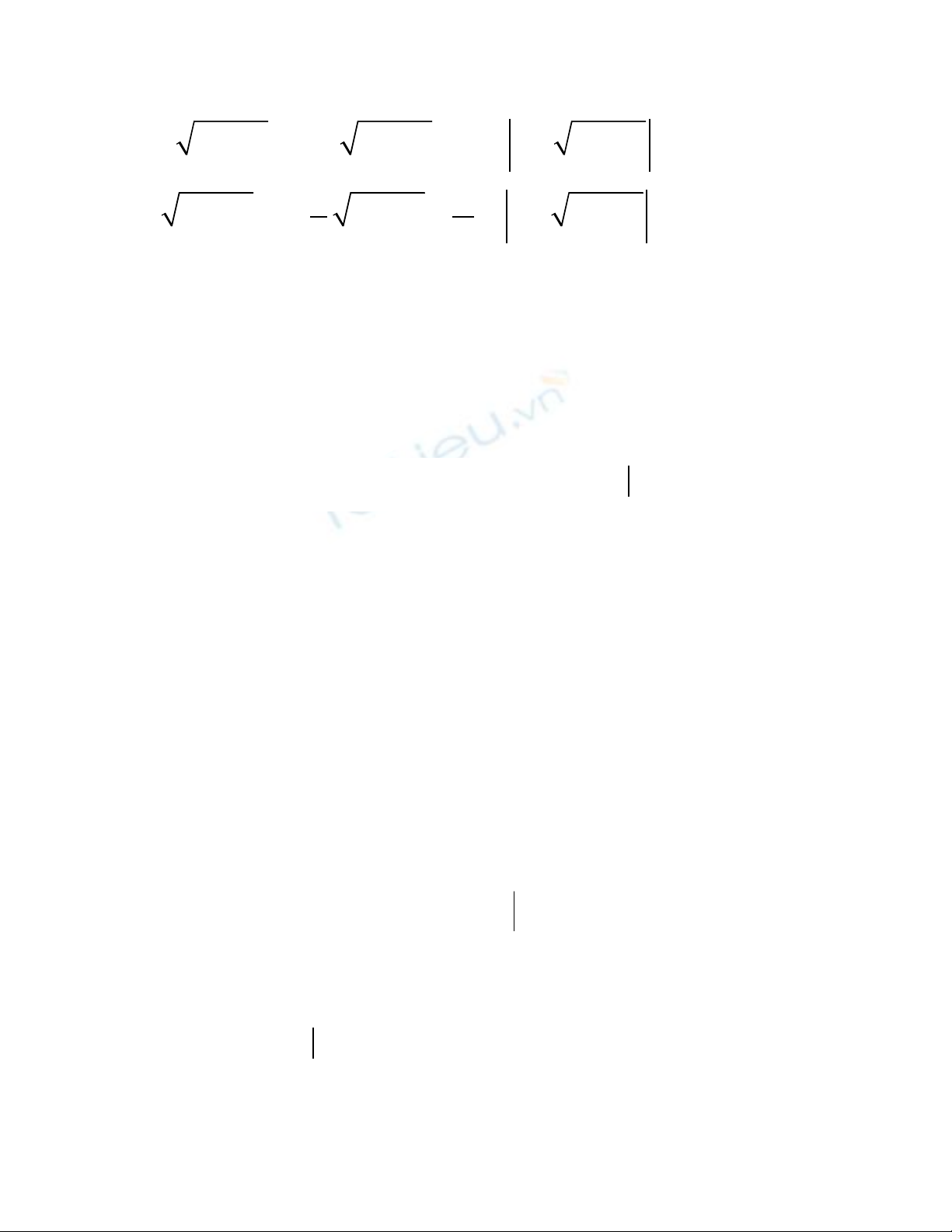
2 2 2
2 lnx Adx x x A A x x A C
+ = + + + + +
+
2 2 2
ln
2 2
x A
x Adx x A x x A C
+ = + + + + +
+
Các ph ng pháp tính tích phân:ươ
Ph ng pháp đ i bi n: có hai ph ng pháp đ i bi nươ ổ ế ươ ổ ế
Đ i bi n d i d u tích phânổ ế ướ ấ
C n tính tích phân ầ
( )f x dx
f
. Gi s có th tìm đ c hàm kh vi ả ử ể ượ ả
( )u x
ϕ
=
và hàm g(u) sao cho bi u th c d i d u tích phân ể ứ ướ ấ
( )f x dx
f
có th vi tể ế
d i d ng:ướ ạ
[ ]
'
( )
( ) ( ) . ( ) ( )
u x
f x dx g f x x dx g u du
ϕ
ϕ
=
= =
� � �
Phép bi n đ i này th ng đ c g i là ph ng pháp đ i bi n ế ổ ườ ượ ọ ươ ổ ế
( )u x
ϕ
=
d i d u tích phân, t c là bi n x thay b ng bi n m i ướ ấ ứ ế ằ ế ớ
( )u x
ϕ
=
.
Nh n xét: M c đích c a ph ng pháp đ i bi n ậ ụ ủ ươ ổ ế
( )u x
ϕ
=
là vi c tínhệ
tích phân
( )f x dx
f
đ c đ a đ n tí ch phân ượ ư ế
( )g u du
g
, th ng đ n gi nườ ơ ả
h n tích phân ban đ u. Sau này khi l y tích phân, ta ph i th ơ ầ ấ ả ế
( )u x
ϕ
=
vào
k t qu tìm đ c.ế ả ượ
Ph ng pháp tính tích phân t ng ph n:ươ ừ ầ
N u u(x) và v(x) là hai hàm s có đ o hàm liên t c trên đo n [ a ; b ] thìế ố ạ ụ ạ
công th c tính tích phân t ng ph n sau đây đ c th a mãn.ứ ừ ầ ượ ỏ
( ) ( ) ( ) ( ) ( ) ( )
' '
b b
b
a
a a
u x v x dx u x v x u x v x dx
= −� �
� �
� �
Hay
.
b b
b
a
a a
udv u v vdu
= −
� �
Gi i thích:ả