
NGHIÊN CỨU ĐỘNG LỰC HỌC
CỦA HỆ CẦN TRỤC - PHAO NỔI
PGS. TS. NGUYỄN VĂN VỊNH
ThS. NGUYỄN HỮU CHÍ
Bộ môn Máy xây dựng - Xếp dỡ
Khoa Cơ khí
Trường Đại học Giao thông Vận tải
Tóm tắt: Bài báo trình bày tóm tắt những kết quả nghiên cứu động lực học của cần trục
đặt trên hệ cần trục - phao nổi khi làm việc hệ tỳ đáy xuống lòng sông. Kết quả cứu thu được
có thể sử dụng làm tài liệu tham khảo có ích để phục vụ cho việc thiết kế, chế tạo hệ này trong
thực tế.
Summary: The paper summarizes the dynamics research results of the floating crane
when the bottom of the floating crane is located on the bottom of river bed. The obtained
research results can be used as useful reference materials to design and manufacture of this
floating crane in practice.
I. ĐẶT VẤN ĐỀ
CT 2
Hiện nay ở khu vực đồng bằng Nam Bộ, để thực hiện công tác xếp dỡ hàng hóa, nạo vét
kênh rạch, phục vụ việc thi công cầu, xây dựng các công trình thủy… trên địa hình sông ngòi,
kênh rạch chằng chịt, người ta thường sử dụng cần trục bộ đặt trên một phao nổi. Hệ này được
gọi là hệ cần trục - phao nổi. Hệ cần trục - phao nổi trong một số trường hợp khi làm việc do
mực nước thủy triều thấp nên tỳ đáy phao xuống lòng sông. Cần trục đặt trên phao (thường là sà
lan) làm việc như ở trên cạn. Lúc này cần phải tính toán cần trục theo quan điểm động lực học
để tính liên kết giữa phao và cần trục nhằm đảm bảo an toàn.
Bài báo này trình bày những kết quả tính toán động lực học của hệ cần trục - phao nổi
trong trường hợp đặc biệt khi làm việc nhưng thường xảy ra trong thực tế như đã nêu ở trên.
II.NỘI DUNG
2.1. Cấu tạo và nguyên lý hoạt động của một hệ cần trục - phao nổi
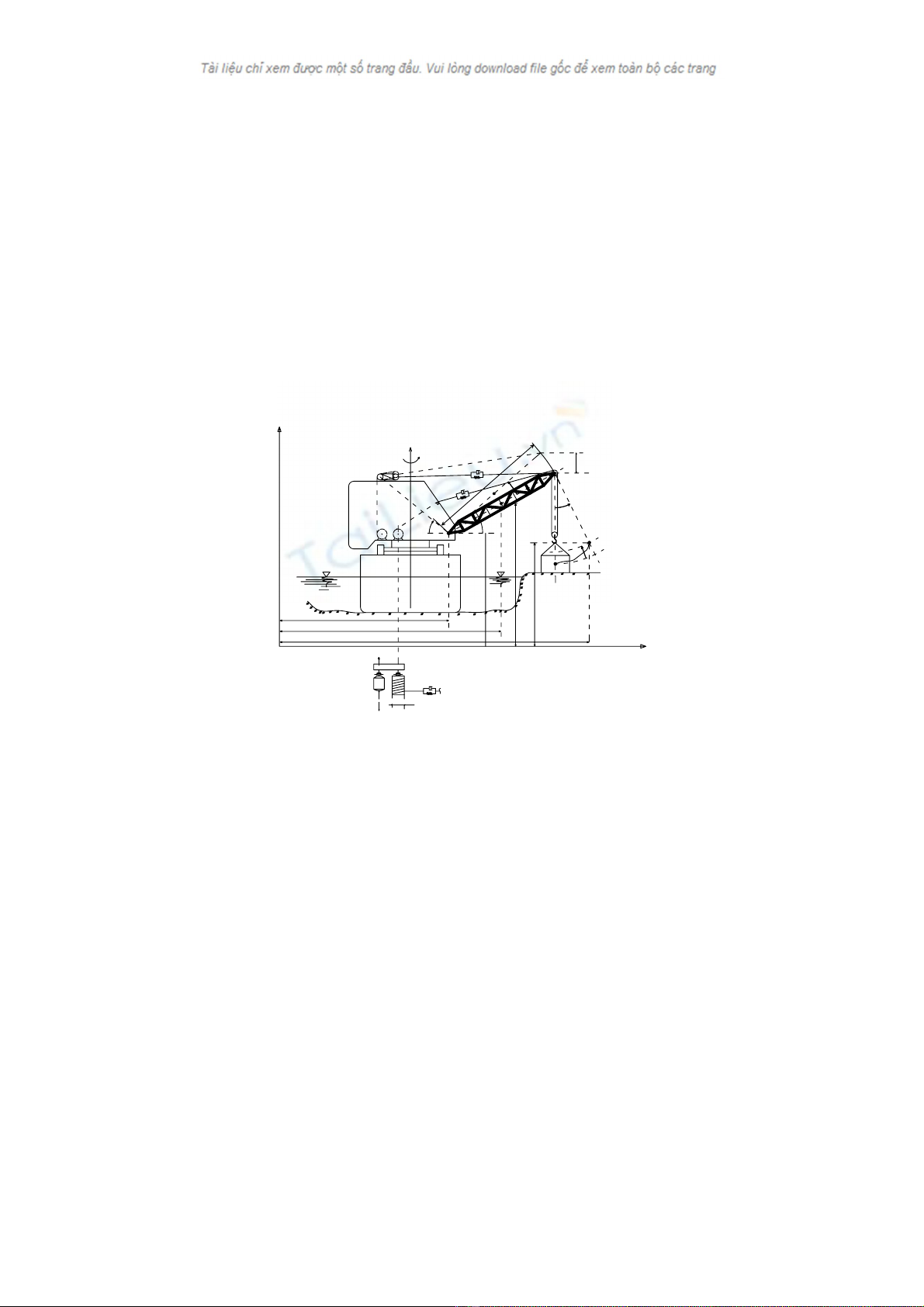
a. Cấu tạo: Cấu tạo của hệ được thể hiện trên hình1.
b. Nguyên lý hoạt động: Sự hoạt động của hệ thông qua cần trục đặt trên phao.
Khi làm việc, các bộ máy nâng - hạ hàng, bộ máy thay đổi tầm với, bộ máy quay ... của cần
trục hoạt động. Người lái sẽ điều khiển các bộ máy này để thao tác các công việc của cần trục.

Nó có thể bốc dỡ hàng theo mọi hướng nhờ bộ máy quay của cần trục.
Hình 1. Hệ cần trục - phao nổi đang nạo vét kênh mương bằng gầu ngoạm
CT 2
2.2. Nghiên cứu động lực học của hệ cần trục – phao nổi
Trong quá trình làm việc của cần trục đặt trên hệ cần trục - phao nổi, nhiều trường hợp do
nước thuỷ triều rút, mực nước thấp nên hệ phao nổi (sà lan) lúc này tỳ xuống lòng sông và như
vậy có thể sử dụng những giả thiết sau đây để xây dựng mô hình động lực học (ĐLH).
2.2.1. Xây dựng mô hình động lực học
a. Các giả thiết
- Phao nổi (sà lan) tỳ đáy xuống lòng sông, giả thiết về cơ chế tiếp xúc đè lên lớp bùn nhão
có nước của đáy phao và đáy sông phẳng, sà lan có vật liệu và kết cấu đủ cứng để có thể coi cần
trục đứng trên nền cứng tuyệt đối (cần trục được liên kết cứng với sà lan và trong trường hợp
này bỏ qua biến dạng của sà lan).
- Dây cáp hàng có độ cứng là S1 và hệ số dập tắt dao động là K1 nó được coi như lò xo có
thể co dãn được.
và hệ số dập tắt dao động là K
- Xét đến độ cứng của cáp cần là S2 2
- Bỏ qua biến dạng của kết cấu thép cần trục.
- Coi vật nâng chỉ dao động trong mặt phẳng của hệ cần trục - phao nổi (mặt phẳng thẳng
đứng chứa cần và toa quay).
- Vật nâng và cụm móc câu được quy dẫn về khối lượng m .
2
- Hàng được nâng lên khi có độ trùng cáp ban đầu δ hoặc không có độ trùng cáp (hàng treo
trong không gian).
- Tải trọng gió tác dụng theo hướng bất lợi cho cần trục.
- Bỏ qua khối lượng ma sát của puly trong hệ thống palăng. Chưa xét đến biến dạng của
các phần tử trong cơ cấu nâng hạ hàng.
.
- Khối lượng của cần được quy dẫn về giữa cần bằng một khối lượng tập trung m3
b. Mô hình động lực học
- Đặt mô hình tính toán vào hệ toạ độ tuyệt đối OXY với các toạ độ suy rộng tương ứng với
các phần tử chuyển động như sau:
Y
X
X
0
X
3
X
2
y
2
y
3
y
0
φ
ϕ
0
A
B
K
2
S
2
K
1
S
1
Δ
H
D
D
1
L
c
m
3
q
3
f
Q
i
2
m
2
q
2
n
q
q
1
i1
K
1
S
1
M(
q1
)
M
f
D
CT 2
Hình 2. Mô hình động lực học của hệ cần trục - phao nổi
q1 - Góc quay của trục động cơ, cơ cấu nâng hạ hàng, rad;
q2 - Độ dịch chuyển của hàng theo phương của cáp nâng hàng, m;
q3 - Góc lắc của cáp hàng quanh đỉnh cần, rad;
qd - Góc quay của tang nâng hàng, rad;
θ
1 - Mômen quán tính quy dẫn của roto động cơ và khớp nối trục;
M(q1) - Đường đặc tính ngoài của động cơ cơ cấu nâng hạ hàng;
Mf - Mômen phanh của cơ cấu nâng hạ hàng;
i1 - Tỉ số truyền của hộp giảm tốc trong cơ cấu nâng hạ hàng;
i2 - Bội suất cáp (số nhánh cáp treo) của cáp hàng;
S2, K2 - Tương ứng là độ cứng và hệ số dập tắt dao động của cáp hàng;
L - Chiều dài của cần của cần trục;
c
D - Đường kính của tang cuốn cáp thuộc cơ cấu nâng hạ hàng;
Pg - Tải trọng gió tác dụng vào cần trục quy dẫn về điểm G;
q4 - Chuyển vị góc của cần (góc lắc của cần xung quanh khớp O);
φo - Góc nghiêng của tâm cần so với phương ngang;
f - Chiều dài cáp hàng;
Q
xo-yo - Toạ độ ban đầu của điểm O.
2.2.2. Thiết lập phương trình chuyển động
Để thiết lập phương trình chuyển động,chúng tôi sử dụng phương trình Lagrănge loại II có

dạng như sau:
i
ii
ii
dT T T u
( ) Q (i 1, 2, 3....n)
dt q q
qq
••
∂∂∂∂
−+ += =
∂∂
∂∂
Trong đó i là số bậc tự do của hệ
a. Xét trường hợp nâng hàng có độ trùng cáp ban đầu δ
Quá trình nâng hàng xảy ra theo ba pha sau đây:
Pha I: Cho động cơ bắt đầu hoạt động, tang bắt đầu cuốn cáp, độ trùng cáp δ Æ 0 (bắt đầu
cáp căng).
Pha II: Tang tiếp tục cuốn cáp, lực căng cáp có giá trị tăng dần Fc = 0 tăng đến giá trị lực
căng tĩnh mg
2
F
ct i2
=
mg
2
F
ct i2
≥
Pha III: Tang tiếp tục cuốn cáp, khi lúc này hàng thực sự nâng lên khỏi mặt đất
và tiếp tục được nâng lên cao.
Trường hợp này mô hình động lực học có 4 bậc tự do.
Phương trình chuyển động của cơ cấu ở pha 1 như sau:
••
M(q )=θq
11
•
1
CT 2
Pha II: Hệ có 2 bậc tự do q1, q ;
4
Sau khi tiến hành các đạo hàm cần thiết theo phương trình Lagrănge loại II (chi tiết xin
xem ở tài liệu tham khảo [2]).
Biểu diễn phương trình chuyển động dưới dạng ma trận chúng ta có:
•• •
Mq+Kq+Sq=f
Chú ý: pha thứ II kết thúc khi:
mg
2
F
ci2
=
mg
2
F
ci2
>
Pha III: Pha III bắt đầu khi , hàng đi lên thực sự. Hệ có 4 bậc tự do: q , q
1 2, q3, q4
Sau khi tiến hành các đạo hàm cần thiết theo phương trình Lagrănge loại II (chi tiết xin
xem ở tài liệu tham khảo [2]).
Biểu diễn phương trình chuyển động dưới dạng ma trận, chúng ta có dạng sau:
•
•• • •
2
Mq+K q +K qq +K q+Sq=f
1233
Trong đó các ma trận cụ thể như sau:
CT 2
••
Mq=
1
θ
1
q••
22c
m mLA
−
2
q••
.
2
m(f -q)
2Q 2 2c Q 2
mL(f q)B
−
••
3
q
2
3
2c
m
(m )L
4
+
2c 2c Q 2
mL(f q)B
−
-m L A
4
q••
2
1
(q )
•
•
2
Kq =
1 2a 2
-m (f - q ) 2c
mLB
−
2
2
(q )
•
.
2
3
(q )
•
2c Q 2
mL(f q)A
−
−
2c Q 2
mL(f q)A−−
2
4
(q )
•
13
qq
••
••
Kqq=
23
23
qq
••
.
2Q 2
2m (f q )−−
33
qq
••
2c
2m L B
−
43
qq
••
22
21
iKR
2
21
iKR−
1
q•
3
Kq
•
= 2
21
iKR− 2
21
iK
2
q•
.
3
q•
4
q•
















