TR NG Đ I H C K THU T CÔNG NGHI PƯỜ Ạ Ọ Ỹ Ậ Ệ
KHOA KHOA H C C B NỌ Ơ Ả
B MÔN TOÁNỘ
BÀI GI NGẢ
Ch ng I: Hàm s nhi u bi nươ ố ề ế
S ti t: 10 lý thuy t + 5 bài t p, th o lu nố ế ế ậ ả ậ
1.1. Khái ni m m đ uệ ở ầ
1.2. Đ o hàm và vi phân c a hàm s nhi u bi n sạ ủ ố ề ế ố
1.3. C c tr c a hàm s nhi u bi n sự ị ủ ố ề ế ố
1.1. Khái ni m m đ uệ ở ầ
1.1.1. Đ nh nghĩa hàm s nhi u bi n sị ố ề ế ố
Đ nh nghĩa ị
Ta g i hàm s c a n bi n s xác đ nh trên D, ký hi uọ ố ủ ế ố ị ệ
f: D
→
R, là quy lu t cho ng m i x = (xậ ứ ỗ
1
, x
2
, ..., x
n
)
∈
D v i u = f(xớ
1
, x
2
, ..., x
n
)
∈
R.
Ví d :ụ
( )
2
1 2
1 2 2 2
1 2
:
( , )
f R R
x x
x x x f x x x
+
= = +
a
1.1.2. Mi n xác đ nh c a hàm s nhi u bi n sề ị ủ ố ề ế ố
Mi n xác đ nhề ị c a hàm s u = f(M), ký hi u Dủ ố ệ
f
, là t p ậ
các đi m M đ f(M) có nghĩa.ể ể
Ví dụ . Trong R
2
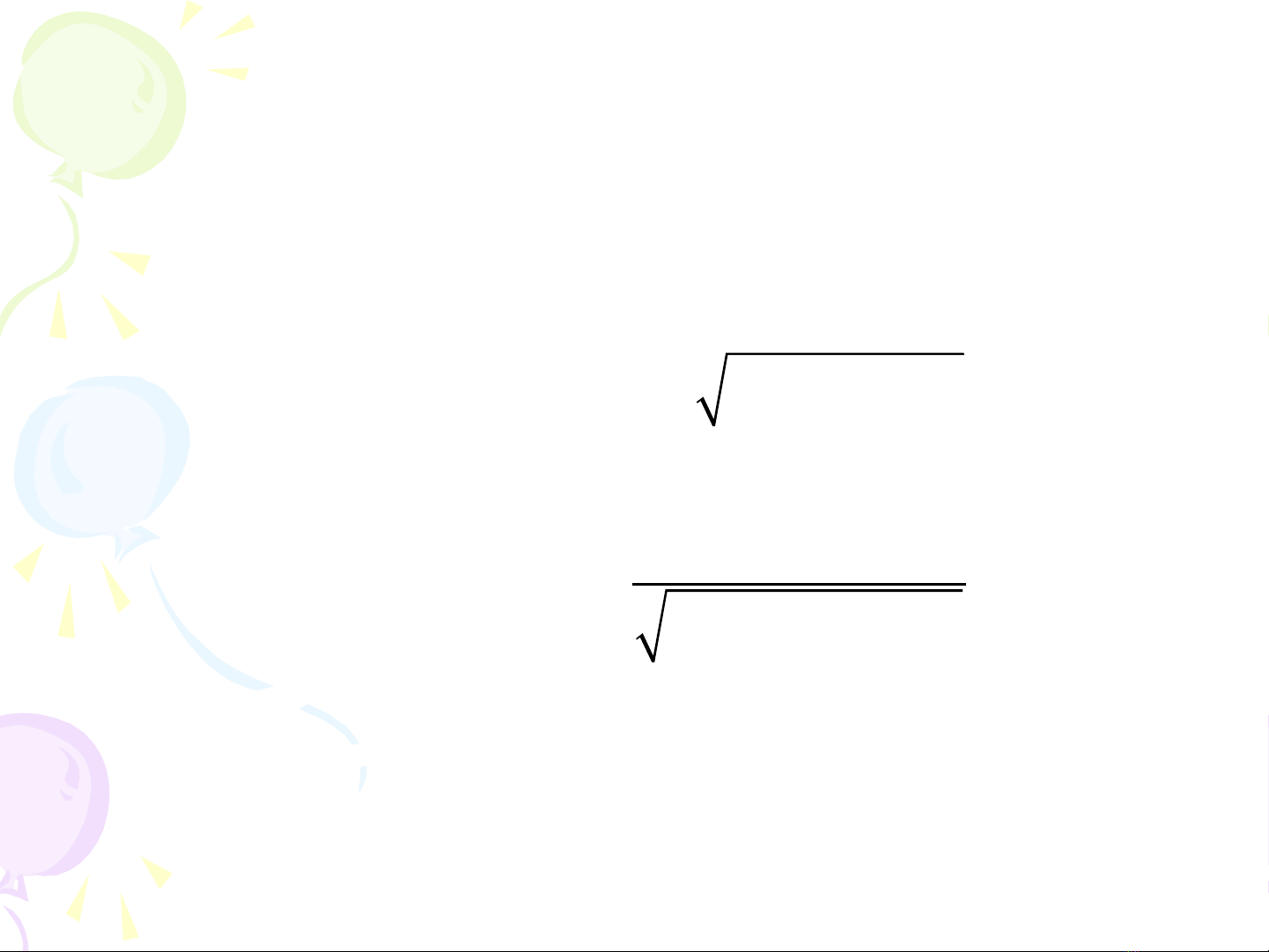
, v i f(x, y) = ớ
2 2
1 x y
− −
thì
D
f
= {(x, y): x
2
+ y
2
≤
1}.
Trong R
3
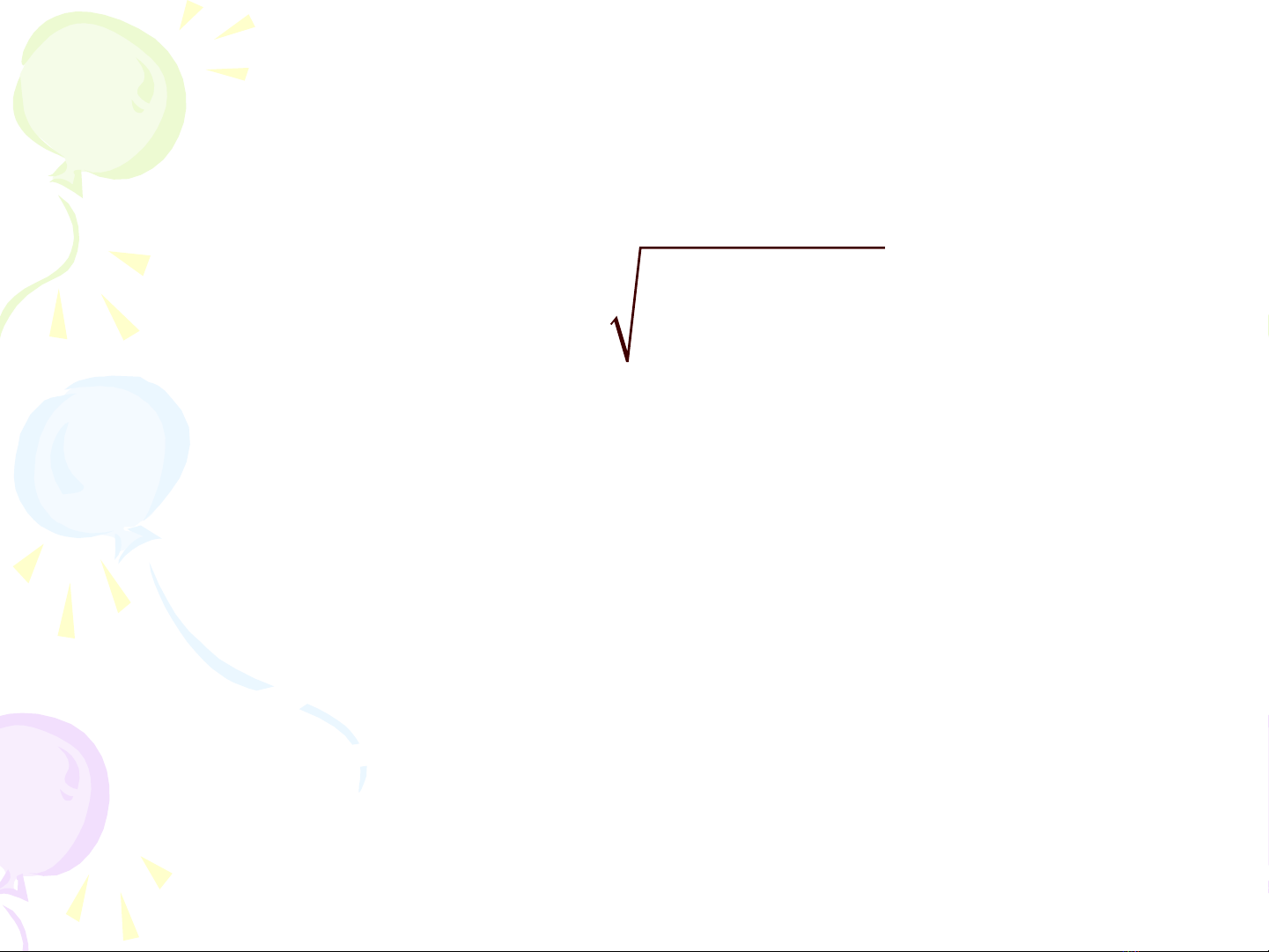
, v i f(x, y, z) = ớ
2 2 2
x
1 x y z
− − −
thì
D
f
= {(x, y, z): x
2
+ y
2
+ z
2
< 1}.
1.1.3. T p h p trongậ ợ
Gi s M(xả ử
1
, x
2
, ..., x
n
) và N(y
1
, y
2
, ..., y
n
)
∈
R
n
• Kho ng cáchả: d(M, N) =
n2
k k
k 1
(x y )
=
−
∑
.
n
R
•
ε
- lân c nậ c a M t p Uủ ậ
ε
(M) = {N
∈
R
n
: d(M, N) <
ε
}.
•
Lân c nậ c a M, ký hi u U(M), là m i t p h p ch a m t ủ ệ ọ ậ ợ ứ ộ
U
ε
(M) nào đó c a Mủ
•
M đ c g i là ượ ọ đi m trongể c a t p E n u t n t i Uủ ậ ế ồ ạ
ε
(M)
n m tr n trong E. ằ ọ
•T p E đ c g i là ậ ượ ọ t p mậ ở n u m i đi m c a nó đ u ế ọ ể ủ ề
là đi m trong.ể