116
Ch−¬ng 11. trao ®æi nhiÖt bøc x¹
1.1.1. C¸c kh¸i niÖm c¬ b¶n
1.1.1.1. §Æc ®iÓm cña qu¸ tr×nh trao ®æi nhiÖt bøc x¹
Trao ®æi nhiÖt bøc x¹ (T§NBX) lµ hiÖn t−îng trao ®æi nhiÖt gi÷a vËt ph¸t
bøc x¹ vµ vËt hÊp thô bøc x¹ th«ng qua m«i tr−êng truyÒn sãng ®iÖn tõ.
Mäi vËt ë mäi nhiÖt ®é lu«n ph¸t ra c¸c l−îng tö n¨ng l−îng vµ truyÒn ®i
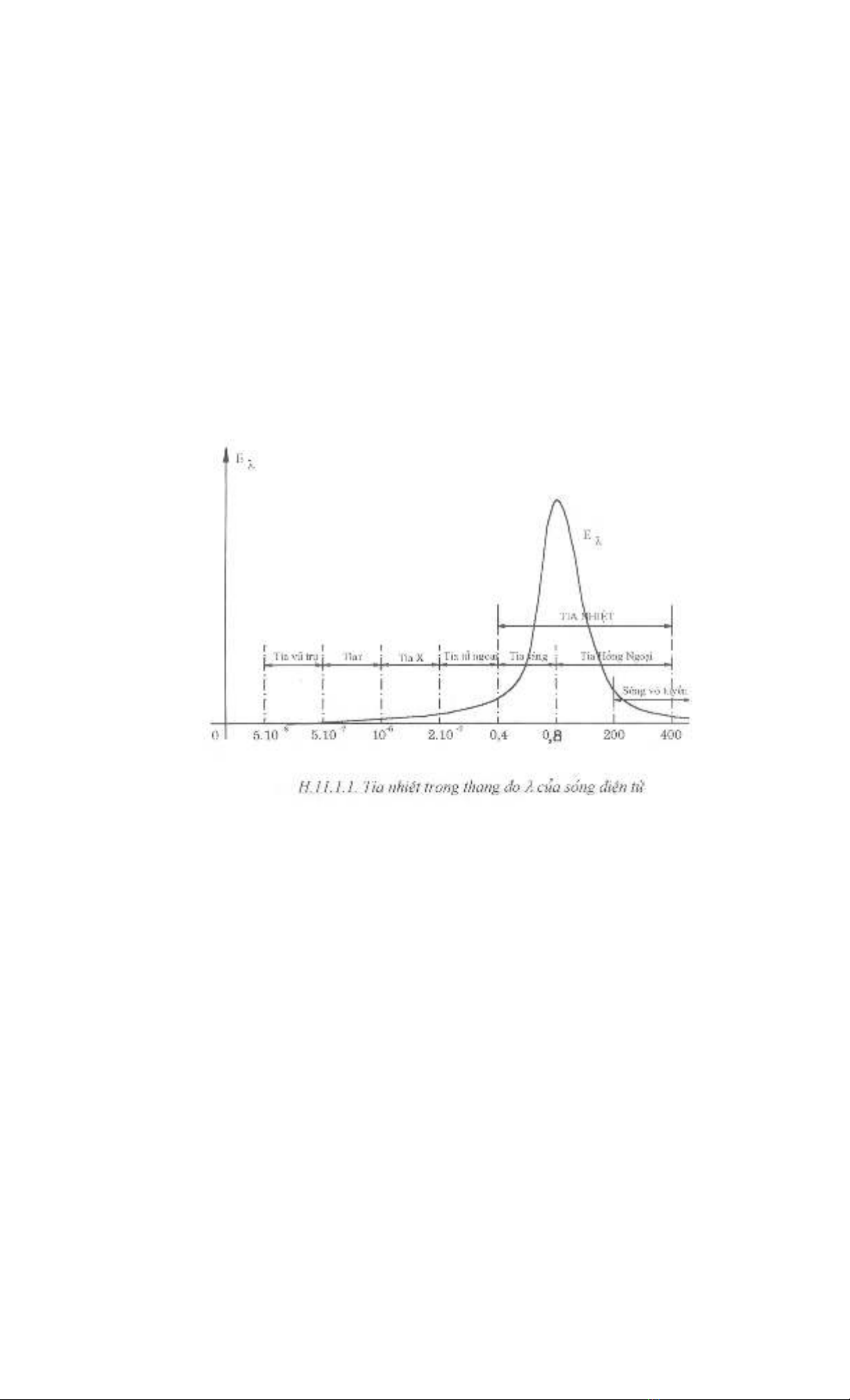
trong kh«ng gian d−íi d¹ng sãng ®iÖn tõ, cã b−íc sãng λ tõ 0 ®Õn v« cïng. Theo
®é dµi bøc sãng λ tõ nhá ®Õn lín, sãng ®iÖn tõ ®−îc chia ra c¸c kho¶ng ∆λ øng
víi c¸c tia vò trô, tia gama γ , tia Roentgen hay tia X, tia tö ngo¹i, tia ¸nh s¸ng, tia
hång ngo¹i vµ c¸c tia sãng v« tuyÕn nh− h×nh (1.1.1.1). Thùc nghiÖm cho thÊy, chØ
c¸c tia ¸nh s¸ng vµ hång ngo¹i míi mang n¨ng l−îng Eλ ®ñ lín ®Ó vËt cã thÓ hÊp
thô vµ biÕn thµnh néi n¨ng mét c¸ch ®¸ng kÓ, ®−îc gäi lµ tia nhiÖt, cã b−íc sãng
λ∈(0,4 ÷ 400) 10-6m.
M«i tr−êng thuËn lîi cho T§NBX gi÷a 2 vËt lµ ch©n kh«ng hoÆc khÝ lâang,
Ýt hÊp thô bøc x¹. Kh¸c víi dÉn nhiÖt vµ trao ®æi nhiÖt ®èi l−u, T§NBX cã c¸c
®Æc ®iÓm riªng lµ:
- Lu«n cã sù chuyÓn hãa n¨ng l−îng: tõ néi n¨ng thµnh n¨ng l−îng ®iÖn tõ
khi bøc x¹ vµ ng−îc l¹i khi hÊp thô. Kh«ng cÇn sù tiÕp xóc trùc tiÕp hoÆc gi¸n tiÕp
qua m«i tr−êng chÊt trung gian, chØ cÇn m«i tr−êng truyÒn sãng ®iÖn tõ, tèt nhÊt lµ
ch©n kh«ng.
- Cã thÓ thùc hiÖn trªn kho¶ng c¸ch lín, cì kho¶ng c¸ch gi÷a c¸c thiªn thÓ
trong kho¶ng kh«ng vò trô.
117
- C−êng ®é T§NBX phô thuéc rÊt m¹nh vµo nhiÖt ®é tuyÖt ®èi cña vËt ph¸t
bøc x¹.
11.1.2. C¸c ®¹i l−îng ®Æc tr−ng cho bøc x¹
11.1.2.1. C«ng suÊt bøc x¹ toµn phÇn Q
C«ng suÊt bøc x¹ toµn phÇn cña mÆt F lµ tæng n¨ng l−îng bøc x¹ ph¸t ra tõ
F trong 1 gi©y, tÝnh theo mäi ph−¬ng trªn mÆt F víi mäi b−íc sãng λ ∈ (0,∞).
Q ®Æc tr−ng cho c«ng suÊt bøc x¹ cña mÆt F hay cña vËt, phô thuéc vµo
diÖn tÝch F vµ nhiÖt ®é T trªn F:
Q = Q (F,T), [W].
11.1.2.2. C−êng ®é bøc x¹ toµn phÇn E
C−êng ®é bøc x¹ toµn phÇn E
cña ®iÓm M trªn mÆt F lµ c«ng suÊt
bøc x¹ toµn phÇn δQ cña diÖn tÝch dF
bao quanh M, øng víi 1 ®¬n vÞ diÖn
tÝch dF:
]m/W[
'dF
Q
E2
δ
=
E ®Æc tr−ng cho c−êng ®é BX
toµn phÇn cña ®iÓm M trªn F, phô
thuéc vµo nhiÖt ®é T t¹i M, E = E (T).
NÕu biÕt ph©n bè E t¹i ∀ M ∈ F th×
t×m ®−îc:
∫
=
F
EdFQ ,
khi E = const, ∀M ∈ F th×:
Q = EF; [W].
11.1.2.3. C−êng ®é bøc x¹ ®¬n s¾c
C−êng ®é bøc x¹ ®¬n s¾c Eλ t¹i b−íc sãng λ, cña ®iÓm M ∈ F lµ phÇn n¨ng
l−îng δ2Q ph¸t tõ dF quanh M, truyÒn theo mäi ph−¬ng xuyªn qua kÝnh läc sãng
cã λ ∈
⎣⎦
λ+÷λ døng víi 1 ®¬n vÞ cña dF vµ dλ:
[]
.m/W,
dF
d
Q
E3
2
λ
δ
=
λ
E
λ ®Æc tr−ng cho c−êng ®é tia BX cã b−íc sãng λ ph¸t tõ ®iÓm M ∈ F, phô
thuéc vµo b−íc sãng λ vµ nhiÖt ®é T t¹i ®iÓm M , Eλ = Eλ (λ, T).
NÕu biÕt ph©n bè Eλ theo λ th× tÝnh ®−îc E = .dE
0λ
∫∞
=λ λQuan hÖ gi÷a Eλ, E,
Q cã d¹ng:
dFdEEdFQ
0
FF λ== ∫∫∫ ∞
=λ
λ
118
11.1.3. c¸c hÖ sè A, D,D,R vµ ε
11.1.3.1. C¸c hÖ sè hÊp thô A, ph¶n x¹ R vµ xuyªn qua D
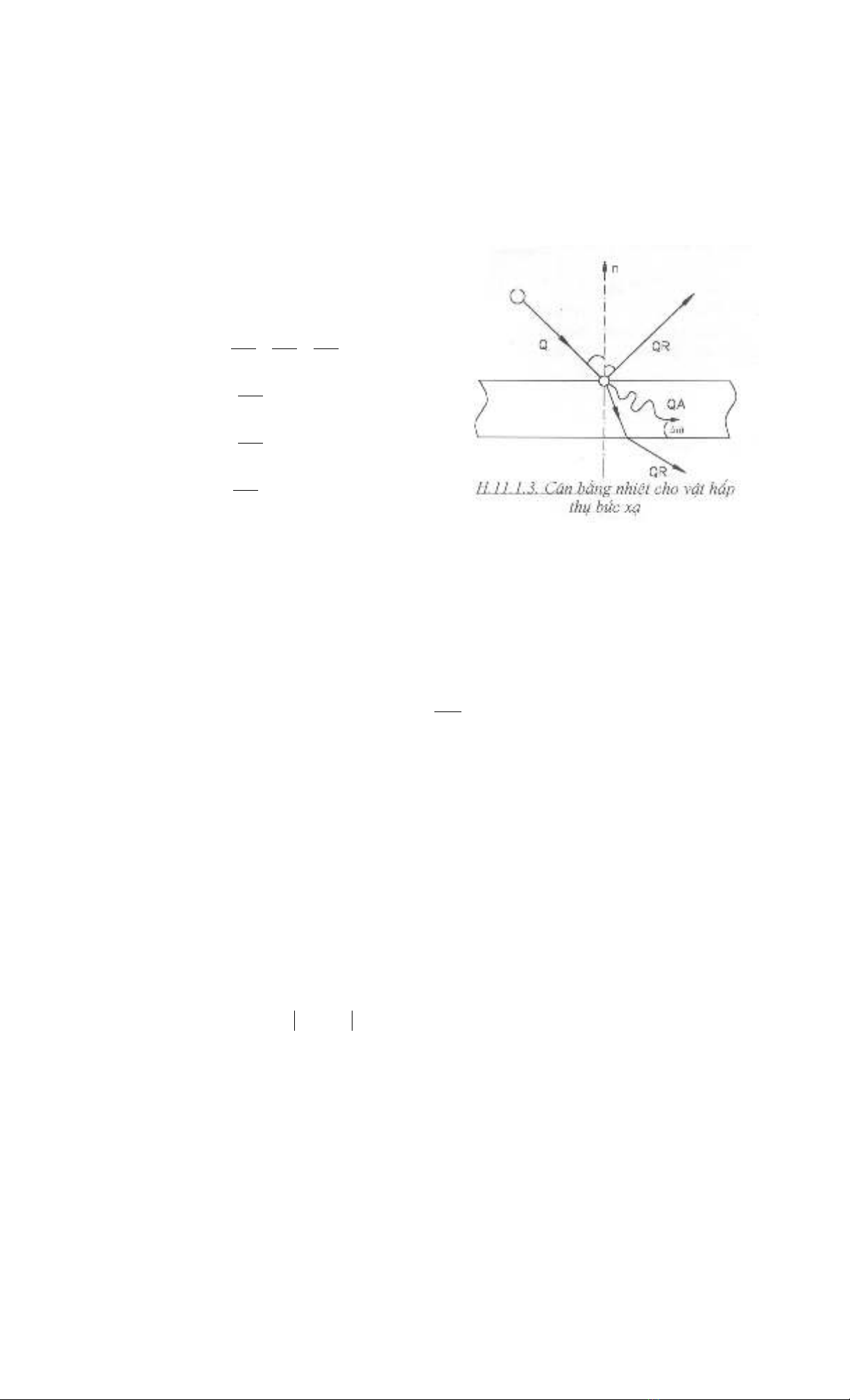
Khi tia sãng ®iÖn tõ mang n¨ng l−îng Q chiÕu vµo mÆt vËt, vËt sÏ hÊp thô 1
phÇn n¨ng l−îng QA ®Ó biÕn thµnh néi n¨ng, phÇn QR bÞ ph¶n x¹ theo tia ph¶n x¹,
vµ phÇn cßn l¹i QD sÏ truyÒn xuyªn qua vËt ra m«i tr−êng kh¸c theo tia khóc x¹.
Ph−¬ng tr×nh c©n b»ng n¨ng
l−îng sÏ cã d¹ng:
Q = QA + QR + QD
Hay
DRA
Q
Q
Q
Q
Q
Q
1DRA ++=++=
Q
Q
AA
= gäi lµ hÖ sè hÊp thô,
Q
Q
RR
= gäi lµ hÖ sè ph¶n x¹.
Q
Q
DD
= gäi lµ hÖ sè xuyªn qua.
Ng−êi ta th−êng gäi vËt cã A = 1 lµ vËt ®en tuyÖt ®èi. R = 1 lµ vËt tr¾ng
tuyÖt ®èi, D = 1 lµ vËt trong tuyÖt ®èi, vËt cã D = 0 lµ vËt ®ôc. Ch©n kh«ng vµ c¸c
chÊt khÝ lo·ng cã sè nguyªn tö d−íi 3 cã thÓ coi lµ vËt cã D = 1.
11.1.3.2. VËt x¸m vµ hÖ sè bøc x¹ hay ®é ®en ε
Nh÷ng vËt cã phæ bøc x¹ Eλ ®ång d¹ng víi phæ bøc x¹ E0λ cña vËt ®en
tuyÖt ®èi ë mäi b−íc sãng λ, tøc cã λ∀=ω=
λ
λ,const
E
E
0
®−îc gäi lµ vËt x¸m, cßn
hÖ sè tØ lÖ ε ®−îc gäi lµ hÖ sè bøc x¹ hay ®é ®en cña vËt x¸m. Thùc nghiÖm cho
thÊy, hÇu hÕt c¸c vËt liÖu trong kÜ thuËt ®Òu cã thÓ coi lµ vËt x¸m. §é ®en phô
thuéc vµo b¶n chÊt vËt liÖu, mµu s¾c vµ tÝnh chÊt c¬ häc cña bÒ mÆt c¸c vËt.
11.1.3.2. Bøc x¹ hiÖu dông vµ bøc x¹ hiÖu qu¶
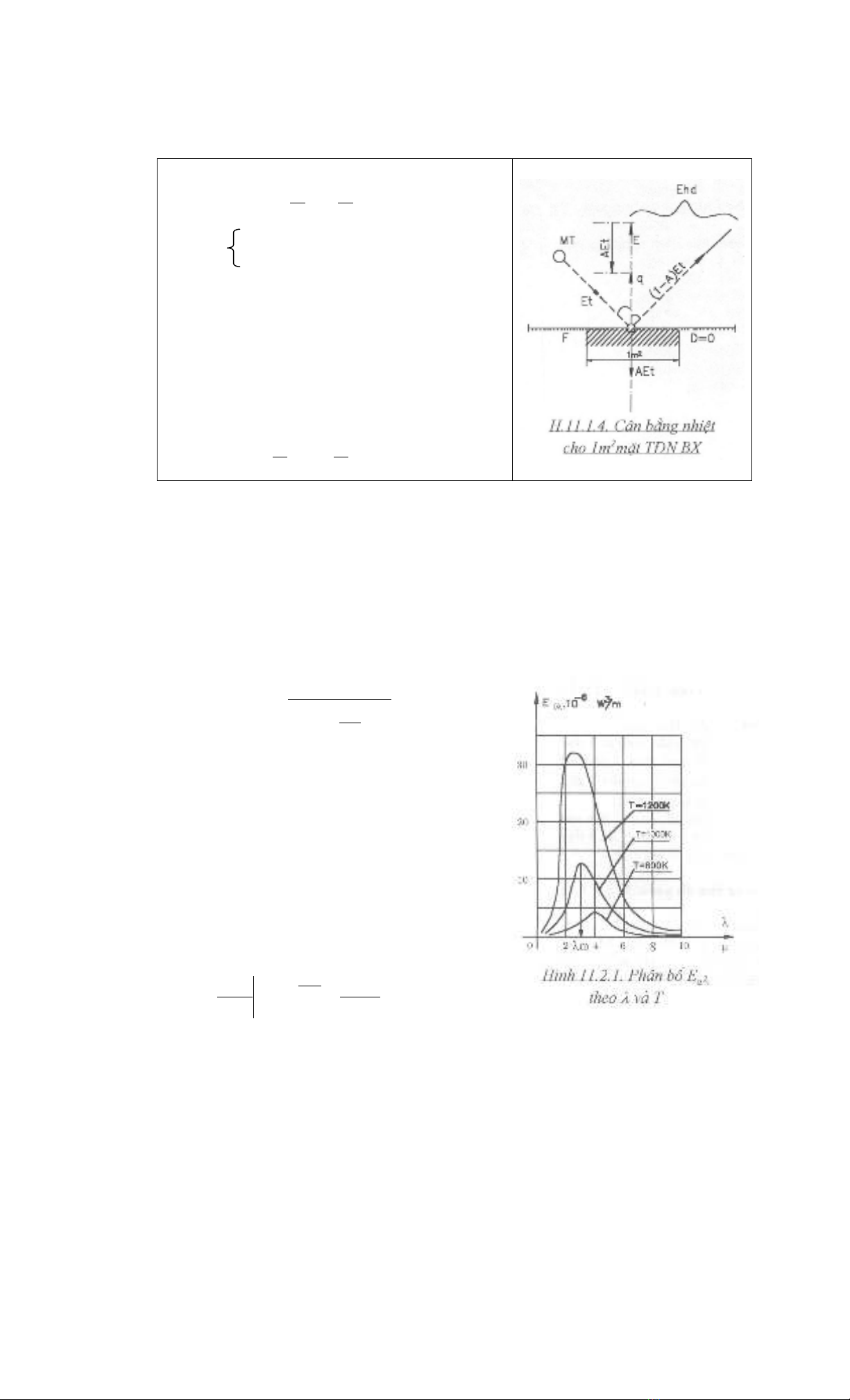
XÐt t−¬ng t¸c bøc x¹ gi÷a mÆt F cña vËt ®ôc cã c¸c th«ng sè D = 0, A , E
vµ m«i tr−êng cã c−êng ®é bøc x¹ tíi mÆt F lµ Et.
- L−îng nhiÖn bøc x¹ ra khái 1 m2 mÆt F, bao gåm bøc x¹ tù ph¸t E vµ bøc
x¹ ph¶n x¹ (1 - A) Et, ®−îc gäi lµ c−êng ®é bøc x¹ hiÖu dông:
⎣
⎦
2
'thd m/WE)A1(EE −+=
- TrÞ tuyÖt ®èi cña hiÖu sè dßng nhiÖt ra theo bøc x¹ tù ph¸t E vµ dßng
nhiÖt vµo 1m2 mÆt F do hÊp thô A Et ®−îc gäi lµ dßng bøc x¹ hiÖu qu¶ q,
⎣
⎦
.m/W,AEEq 2
t
−=
119
Dßng bøc x¹ hiÖu qu¶ q chÝnh lµ l−îng nhiÖt trao ®æi b»ng bøc x¹ gi÷a1m2
mÆt F víi m«i tr−êng.
NÕu vËt cã nhiÖt ®é cao h¬n m«i tr−êng, tøc vËt ph¸t nhiÖt th× q = E –
AEt, nÕu vËt thu nhiÖt th× q = AEt – E.
- Quan hÖ gi÷a Ehd vµ q cã d¹ng:
⎟
⎠
⎞
⎜
⎝
⎛−±= 1
A
1
q
A
E
Ehd
dÊu (+) khi vËt thu q,
dÊu (-) khi vËt ph¸t q.
NÕu xÐt tren toµn mÆt F, b»ng c¸ch
nh©n c¸c ®¼ng thøc trªn víi F, sÏ ®−îc:
C«ng suÊt bøc x¹ hiÖu dông cña F lµ:
Qhd = Q +(1 – A)Qt’
⎣
⎦
W.
L−îng nhiÖt trao ®æi gi÷a F vµ m«i
tr−êng lµ:
QF = [Q - AQt], [W].
Quan hÖ gi÷a Qhd, QF lµ:
[]
.W,1
A
1
Q
A
Q
QFhd ⎟
⎠
⎞
⎜
⎝
⎛−±=
11.2. C¸c ®Þnh luËt c¬ b¶n cña bøc x¹
11.2.1. §Þnh luËt Planck
Dùa vµo thuyÕt l−îng tö n¨ng l−îng, Panck ®· thiÕt lËp ®−îc ®Þnh luËt sau
®©y, ®−îc coi lµ ®Þnh luËt c¬ b¶n vÒ bøc x¹ nhiÖt:
C−êng ®é bøc x¹ ®¬n s¾c cña vËt ®en tuyÖt ®èi E0λ phô thuéc vµo b−íc
sãng λ vµ nhiÖt ®é theo quan hÖ:
⎟
⎠
⎞
⎜
⎝
⎛−
λ
λ
=
λ
1
T
C
exp
C
E
2
5
1
0
Trong ®ã C1, C2lµ c¸c h»ng sè phô
thuéc ®¬n vÞ ®ã, nÕu ®o, nÕu ®o E0λ b»ng
W/m3, λ b»ng m, T b»ng 0K th×:
C
1 = 0,374.10-15, [Wm2]
C
2 = 1,439.10-12, [mK]
§å thÞ E0λ (λ,T) cho thÊy: E0λ t¨ng
rÊt nhanh theo T vµ chØ cã gi¸ trÞ ®¸ng kÓ
trong miÒn λ ∈ (08÷ 10).10-6 m.
E0λ ®¹t cùc trÞ t¹i b−íc sãng λm x¸c
®Þnh theo ph−¬ng tr×nh:
,01
T5
c
e
E
m
2
T.m
2c
m
0=−
λ
+=
λ∂
∂λ
λ
λ
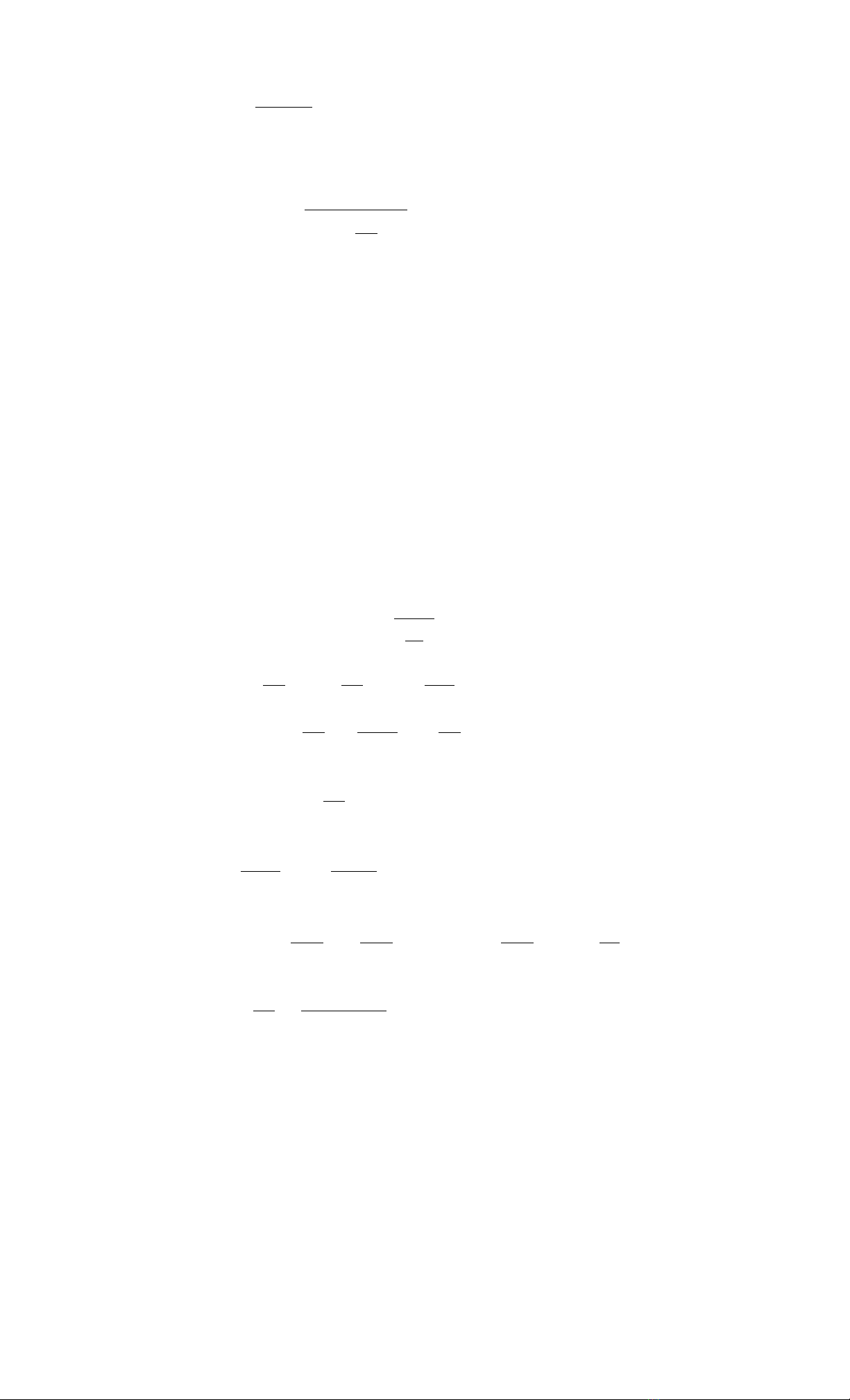
120
tøc lµ t¹i λm
[]
.m,
T
10.9,2 3−
§ã lµ néi dung ®Þnh luËt Wien, ®−îc thiÕt lËp tr−íc Plack b»ng thùc
nghiÖm.
§Þnh luËt Plack ¸p dông cho c¸c vËt x¸m, lµ vËt cã Eλ = εE0λ, sÏ cã d¹ng:
[
]
.m/W,
1
T
C
exp
C
E3
2
5
1
⎟
⎠
⎞
⎜
⎝
⎛−
λ
λ
ε
=
λ
11.2.2. §Þnh luËt Stefan  Boltzmann
a. ph¸t biÓu ®Þnh luËt:
C−êng ®é bøc x¹ toµn phÇn E0 cña vËt ®en tuyÖt ®èi tØ lÖ víi nhiÖt ®é tuyÖt
®èi mò 4:
4
00 TE σ=
Víi σ0 = 5,67.10-8 W/m2K4
§Þnh luËt nµy ®−îc x©y dùng trªn c¬ së thùc nghiÖm vµ lÝ thuyÕt nhiÖt
®éng häc bøc x¹, mang tªn hai nhµ khoa häc thiÕt lËp ra nã tr−íc Planck. Sau ®ã,
nã ®−îc coi nh− 1 hÖ qu¶ cña ®Þnh luËt Planck.
b. chøng minh:
B»ng ®Þnh luËt Planck:
λ
λ
λ
=λ ∫∫ ∞
=λ
−
∞
=λ λd
t
c
C
dEE 02
5
1
000
§æi biÕn x = T
C2
λth× Tx
C2
=λ vµ dx
Tx
C
d2
2
=λ
4
0
4
4
2
1
0
x
3
4
4
2
1
0TTI
C
C
dx
1e
x
T
C
C
Eσ=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
−
=∫
∞
c. TÝnh h»ng sè I
C
C
2
1
0=σ
Víi
()
dxexdxeexdx
e1
ex
dx
1e
x
I00n 0x
x)1n(3
0n
n
xx3
0x
x3
0x
3∫∑∫
∑
∫∫ ∞∞
=
∞
=
+−
∞
=
−−
∞
−
−
∞==
−
=
−
nÕu ®æi biÕn t = (n +1)x th×
5,6
n
1
!3
1n
1
dtet
1n
dt
e
1n
t
I
1n
4
4
0n
t
0t
3t
3
0n 0t ==
⎟
⎠
⎞
⎜
⎝
⎛
+
=
+
⎟
⎠
⎞
⎜
⎝
⎛
+
=∑∑
∫
∑∫∞
=
∞
=
−
∞
=
−
∞
=
∞
=
Do ®ã h»ng sè bøc x¹ cña vËt ®en tuyÖt ®èi, theo Planck lµ:
428
84
154
4
2
1
0Km/W10.67,55,6
10.4388,1
10.37,0
I
C
C−
−
−
===σ
Gi¸ trÞ nµy cña σ0 hoµn toµn phï hîp víi ®Þnh luËt trªn.