1
v(t)
0
t
+A
-A
T0/2-T0/2 T0
CHƯƠNG 3:
PHÂN TÍCH TRONG MIỀN TẦN SỐ
Tín hiệu và hệ thống rời rạc thời gian có thể phân tích trong miền tần số ta sẽ thấy một đặc điểm quan
trọng của hệ thống là đáp ứng tần số.
Phân tích Fourier liên tục thời gian bao gồm chuỗi Fourier và biến đổi Fourier chúng thì hữu
ích cho sự phân tích và thiết kế của tín hiệu và hệ thống liên tục thời gian. Sự phát triển của lý thuyết
xử lý tín hiệu số đặc biêt, biến đổi Fourier rời rạc, và xử lý tín hiệu số cũng như máy tín có thể phân
tích Fourier duy trì trong việc sử dụng.
Sau đây một sự tóm tắt ngắn gọn biến đổi Fourier liên tục thời gian, chuơng này sẽ đưa ra biến
đổi Fourier rời rạc thời gian bao gồm chuỗi Fourier rời rạc thời gian (DTFS) và biến đổi Fourỉe rời rạc
thời gian (DTFT). Phần kế tiếp sẽ thảo luận một khía cạnh quan trọng của DTFT đó là đáp ứng tần số
của hệ thống. DTFT thì liên quan với nhiều biến đổi phổ biến cho sự phân tích và thiết kế hệ thống rời
rạc thời gian, biến đổi z, một chủ đề của chuơng kế tiếp.
Để hòan thành bức tranh về biến đổi Fourier, phần cuối cùng đưa ra một giới thiệu biến đổi
Fourier rời rạc (DFT), đó là phiên bản tần số đuợc lấy mẫu của DTFT. DFT và những ứng dụng của nó
vuợt trội hơn những phân tích Fourỉe khác. Chúng thì đuợc nêu ra chi tiết trong chuơng 8.
3.1 CHUỖI FOURIER LIÊN TỤC THỜI GIAN (CTFS)
Phân tích Fourier liên tục thời gian bao gồm chuỗi Fourier và biến đổi Fourier, hoặc tích phân Fourier.
Phân tích Fourier liên tục thời gian không đuọec trình bày chi tiết nhưng sẽ là cái nhìn tổng quát.
3.1.1: Chuỗi lƣợng giác
Nhà toán học nổi tiếng người Pháp Jean Baptiste Joseph Fourier đã minh họa rằng một sóng tuần hoàn
có thể phân tích thành một chuỗi vô hạn của những thành phần sin và cosin có những tần số là tích của
tần số cơ bản của sóng.
Bắt đầu với tín hiệu thời gian
)(tx
(Hình.3.1), tuần hoàn tại chu kỳ T0 (s) hoặc tần số gốc
00 /2 T
(rad/sec) hoặc tần số F0 = 1/T0 (Hz). Khai triển lượng giác là
10
100 sincos)(
n
n
n
ntbtnaatx
(3.1)
Ở đây những hệ số được cho bởi
x(t)
Hình.3.1: Một sóng tuần hoàn với chu kỳ To
2
2/
2/
0
00
0)(
1T
Tdttx
T
a
(3.2a)
2/
2/ 0
0
0
0cos)(
2T
T
ntdtntx
T
a
(3.2b)
2/
2/ 0
0
0
0sin)(
2T
T
ntdtntx
T
b
(3.2c)
Tích phân trên giới hạn ở –T0/2 và T0/2, nhưng giới hạn khác có thể được sử dụng cùng với khoản cách
giữa chúng là chu kỳ T0, ví dụ 0 và T0.
Những thành phần khai triển chứa đựng ý nghĩa sau:
a0 : Trung bình của tín hiệu (hoặc thành phần DC)
a1cos
0t + b1sin
0t : Thành phần cơ bản (nhớ tổng của hai sin có cùng tần số là sin tại tần
số đó, (xem phần (3.3)) , hoặc họa tần thứ nhất.
a2cos0t + b2sin0t : Họa tần thứ hai
a3cos0t + b3sin0t : Họa tần thứ ba
…
Ví dụ 3.1.1
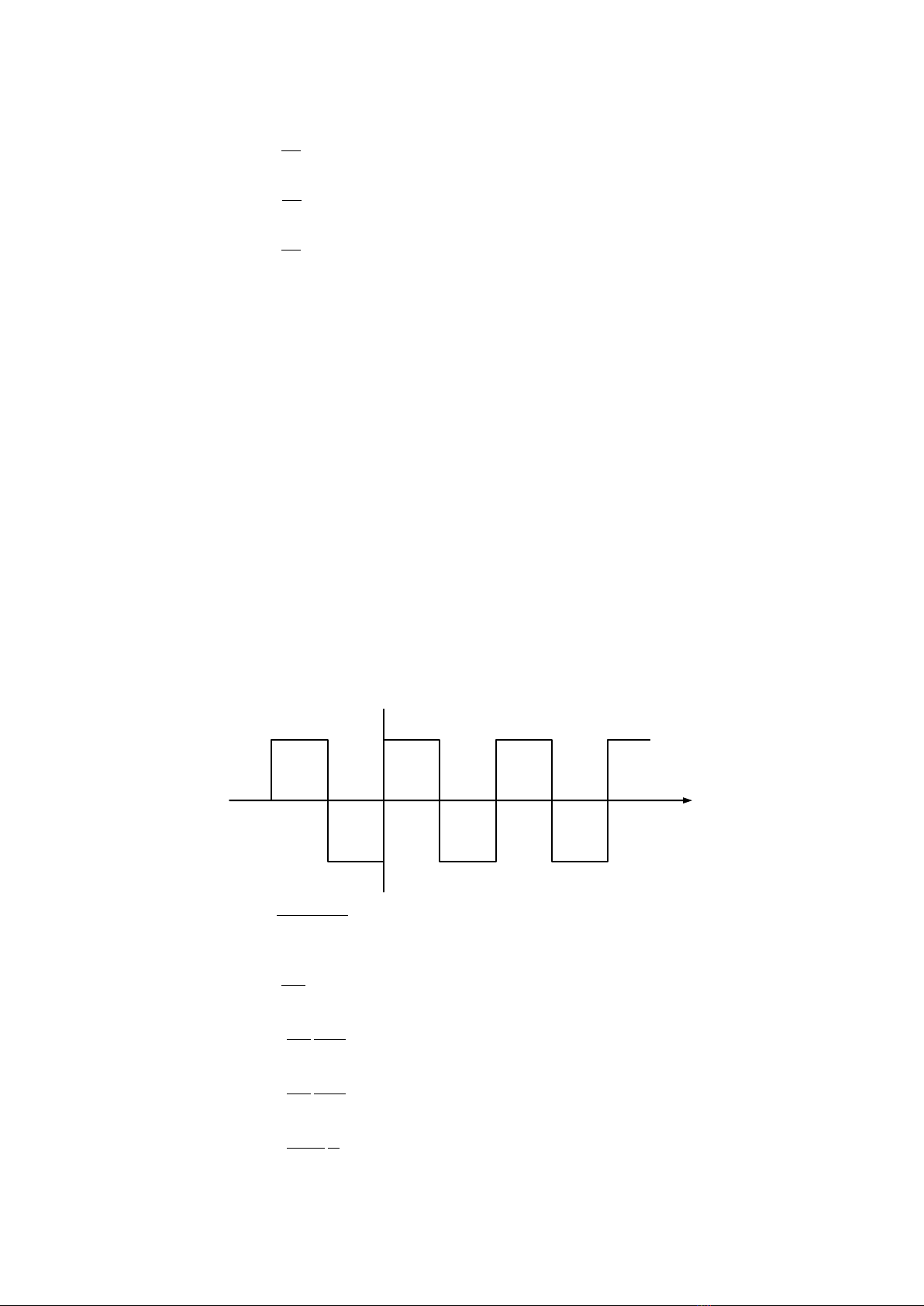
Tìm chuỗi Fourier cho sóng vuông đối xứng hình 3.2
Giải
Ta quan sát trực tiếp rằng thành phần DC là 0 vì phần dương và âm của tín hiệu bằng nhau.
a0 =0
Tất nhiên, khi sử dụng công thức (3.2a), ta sẽ có cùng kết quả. Kế đến, vì sóng là bất đối xứng, có
nghĩa, đối xứng qua gốc, thành phần cosin bằng 0:
an =0 , với tất cả n
Thành phần sin còn lại được cho bởi
even n ,011
1
2
4
cos
14
cos
14
sin
4
2/
0
0
00
2/
0
0
00
0
2/
0
0
0
0
0
n
A
tn
nT
A
tn
nT
A
tdtn
T
A
b
T
T
T
n
+A
-A
0
t
v(t)
T0/2
T0/2
T0
Hình.3.2 : Ví dụ 3.1.1 (sóng vuông đối xứng)
3
n
A
n
A1
2
4
11
1
2
4
, n lẻ
Những hệ số
n
b
có thể đặt trong hình thức ngắn gọn:
)12(
14
n
A
bn
, n = 1, 2, 3, …
Vì vậy chuỗi Fourier là
tn
n
A
tx
n0
1
)12sin(
)12(
14
)(
, n = 1, 2, 3, …
...5sin
5
1
3sin
3
1
sin
4
000 ttt
A
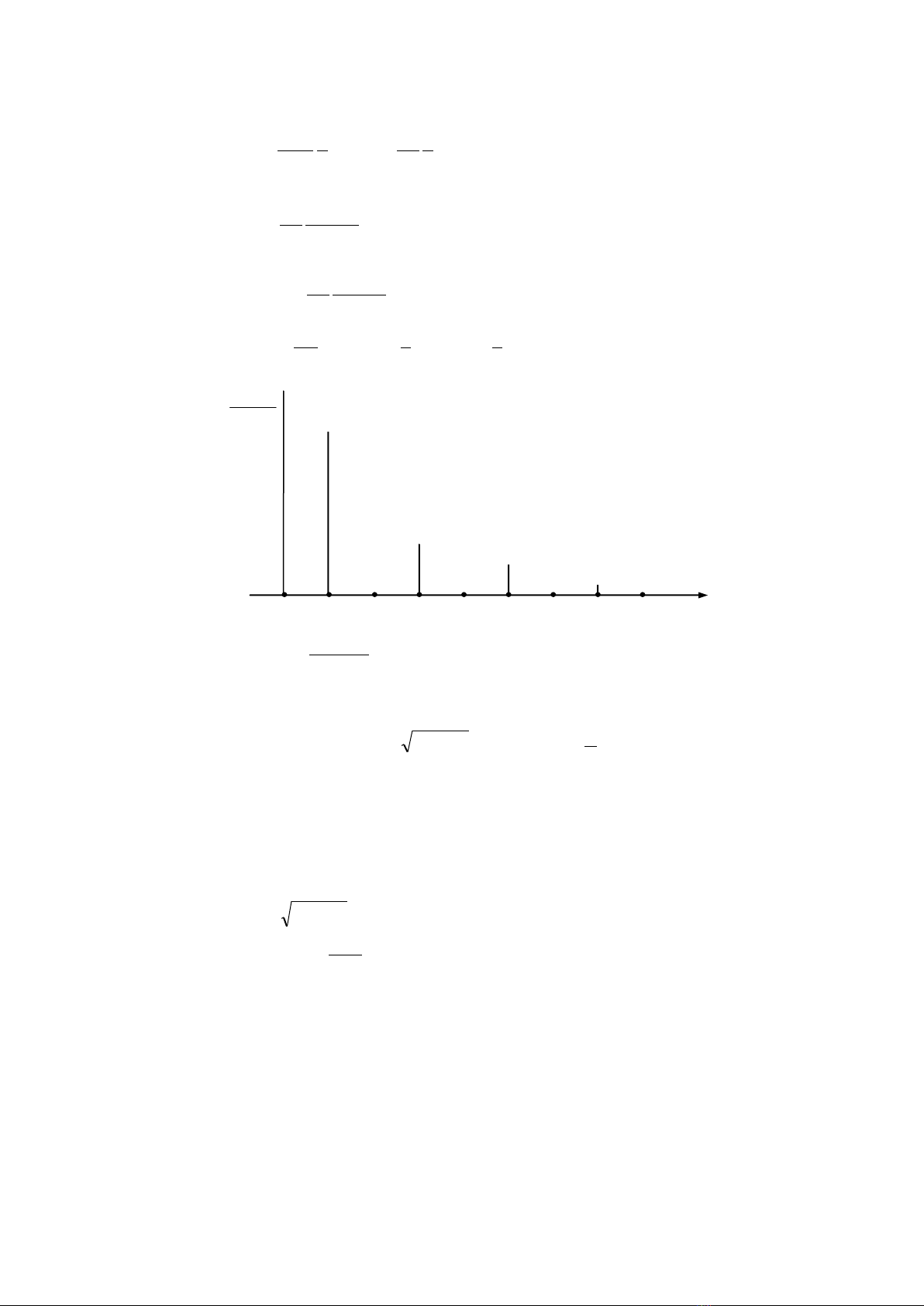
Hình 3.3 là hình vẽ những hệ số được chuẩn hóa tương ứng với sự chuẩn hóa tần số gốc.
Ta biết rằng tổng của hai sin có cùng tần số là một sin cùng tần số đó, đặc biệt
a
b
tbatbta 122 tancossincos
(3.3)
Vì điều này, công thưc (3.1) có thể thay đổi sang dạng của biên độ và pha:
)Φcos()( 0
1n
00n tncctx
(3.4)
Với
00 ac
(3.5a)
22
nnn bac
(3.5b)
n
n
na
b
1
tan
(3.5c)
Trong sự phân tích này ta có thể nhận thấy
0
c
là thành phần trung bình,
)cos( 101 tc
thành phần
tần số cơ bản, và
)2cos( 202 tc
họa tần thứ hai...
Hình vẽ của những hệ số so với tần số là phổ biên độ (Hình 3.3), và hình vẽ pha
n
so với tần
số là phổ pha. Cả hai phổ là rời rạc hoặc phổ đường.
Ví dụ 3.1.2
Tìm phân tích Fourier của sóng trong ví dụ 3.1.1 trong hình thức biên độ và pha.
Giải
Những hệ số là
1
/4A
bn
1/7
/0
8
7
6
5
4
3
2
1
0
Hình.3.3: Ví dụ 3.1.1 (Phổ biên độ )
1/5
1/3
4
00 ac
cn =
22
nn ba
= bn
n = tan-1
n
n
a
b
= – 90O ( = –/2)
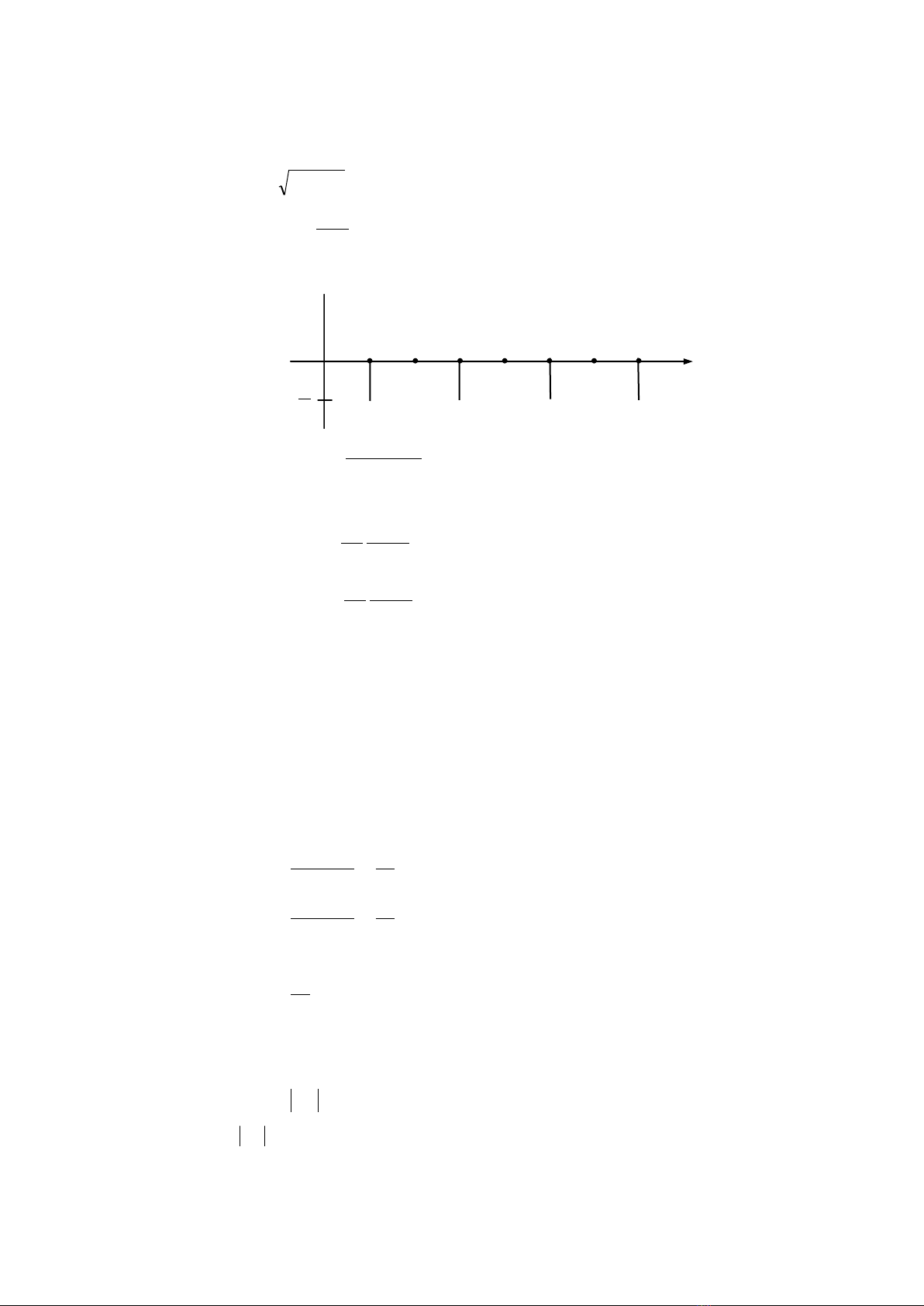
Phổ biên độ như trước, phổ pha được cho trong hình 3.4
Sự phân tích diễn tả như sau:
1n
t1-2n
1-2n
14A
tx 0
090)(cos)(
1n
t1-2n
1-2n
14A
0
)cos(
3.1.2 Khai triển dạng mũ
Khai triển Fourier dạng mũ phức được dùng hơn vì nó thể hiện được biên độ và pha, dẽ liên hệ với
biến đổi Fourier.
n
tjn
neXtx 0
)(
(Tổng hợp công thức) (3.6)
Hai thành phần đối xứng
n
X
và
n
X
luôn luôn xuất hiện theo cặp và tổng của mỗi cặp là thực. Sự
liên hệ giữa mũ phức và hệ số lượng giác là
00 caX0
(3.7a)
n
j
nnn
ne
cjba
X
22
(3.7b)
n
j
nnn
ne
cjba
X
22
(3.7c)
Những hệ số
n
X
có thể được tính trực tiếp từ
O
T
0
tjn
0
ndtx(t)e
T
1
X0
(phân tích công thưc) (3.8)
Ngưỡng của tích phân có thể là
/T- 2
0
và
/T 2
0
thay vì 0 và T như trên
Vì những hệ số
n
X
là nói chung là phức, ta viết
n
j
nn eXX
(3.9)
Biến thiên của
Xn
là phổ biên độ, biến thiên của
n
là phổ pha của tín hiệu. Với một tín hiệu thực,
phổ biên độ là đối xứng chẵn (đối xứng) và phổ pha là đối xứng lẻ (bất đối xứng)
n
0
/
7
6
5
4
3
2
1
0
2
Hình.3.4: Ví dụ 3.1.2 (Phổ pha)
5
Ví dụ 3.1.3
Tìm khai triển Fourier của chuỗi xung đồng nhất.
Giải
Xét một chuỗi xung đồng nhất
)(tA
trong khoản chu kỳ
0
T
(Hình.3.5a):
k
kTtAtx )()( 0
Những hệ số khai triển được cho bởi
000
0
/2 0
/2
0 0 0
11
( ) ( )
Tjn t jn
nT
A
X A t e dt A t e dt
T T T
Hình.3.5 là phổ biên độ. Từ những hệ số ta có thể tổng hợp tín hiệu như:
n
tjn
e
T
A
tx 0
0
)(
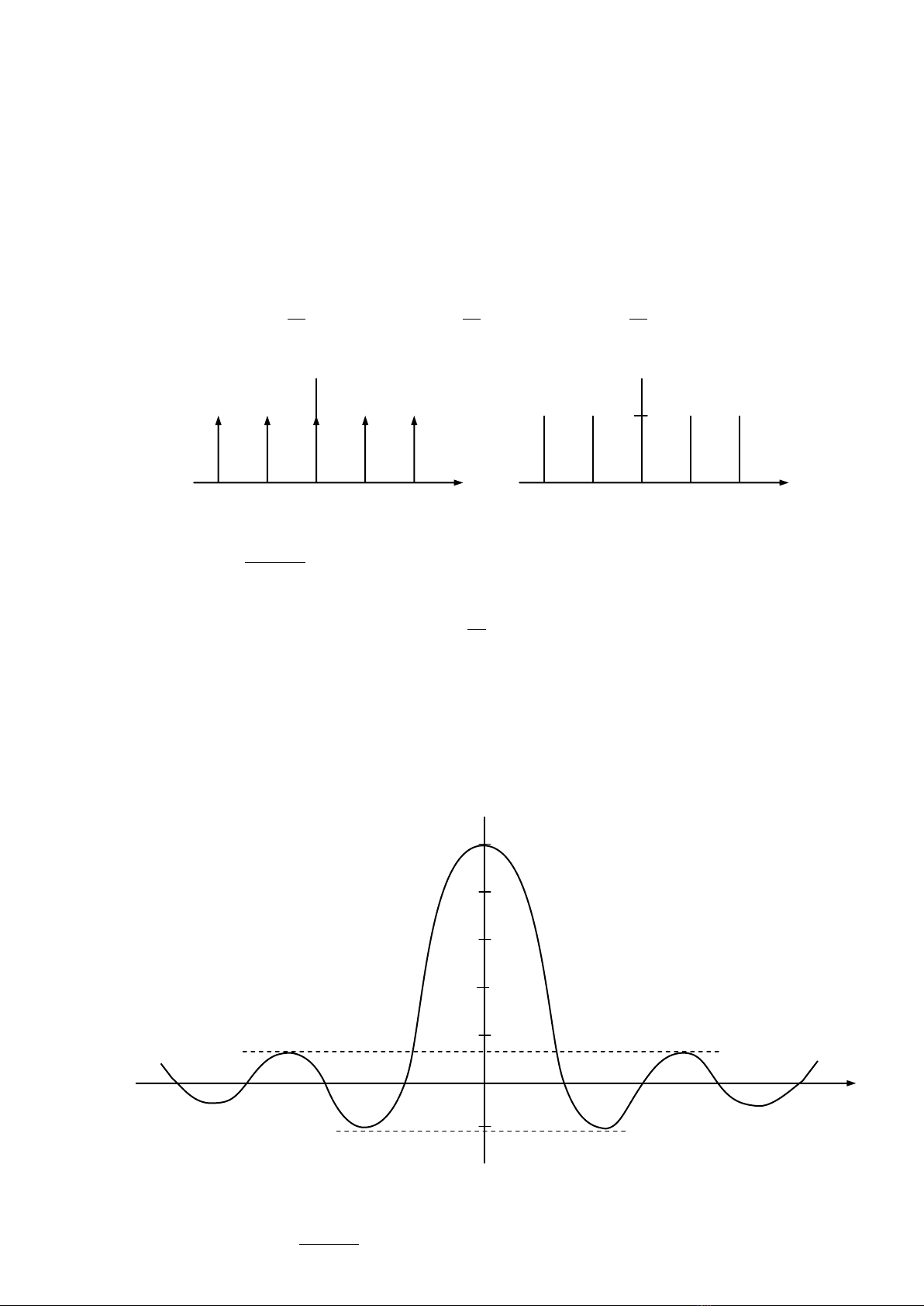
3.1.3 Hàm sinx/x
Xem sự phân tích Fourier, đây là một hàm đặc biệt
sinx/x
(hoặc hàm
sincx
, hoặc hàm
Sa(x)
). Chú
ý ở đây ta viết sinx / x to nghĩa hoặc sin(x) / x . Biến thiên trên
sinx/x
với x được chỉ trong hình 3.6.
Nó là một hàm đối xứng với vùng đơn vị, có giá trị lớn nhất là 1 tại gốc, và 0 xuyên qua tại khoảng .
Khoản cách giữa gốc và điểm không đầu tiên là .
x(t)
A
t
2T0
T0
0
–T0
–2T0
(a)
Xn
A/T0
0
/
2
1
0
–1
–2
(b)
Hình.3.5: Ví dụ 3.1.4 (tín hiệu và phổ của nó)
x
0
0.2
0.4
0.6
0.8
– 0.2178
2
3
4
–
–2
–3
–4
sinx/x
0.1284
1.0
Hình.3.6: Hàm sinx/x (hoặc sincx, hoặc Sa(x))