ChƯ¬ng Iii:
phƯ¬ng ph¸p sö dông §Æc tÝnh
trong qu¸ tr×nh khai th¸c
hÖ ®éng lùc tµu thñy
1
@ 3.1. Ph¬ng ph¸p s ö dông ®Æc tÝnh cña H§L ®éng c¬ lai ch©n vÞt
biÕn bíc.
.1.1. Ph¬ng ph¸p gÇn ®óng x¸c ®Þnh th«ng sè c«ng t¸c cña ®éng c¬ lai ch©n vÞt
biÕn bíc.
Víi H§L ®éng c¬ lai CVBB viÖc thay ®æi tèc ®é vµ chiÒu ch¹y tµu ngoµi viÖc thay
®æi tèc ®é vµ chiÒu quay ®éng c¬ cßn cã thÓ th«ng qua viÖc thay ®æi bíc ch©n
vÞt (H/D).
ViÖc lùa chän chÝnh x¸c cÆp th«ng sè (n – H/D) cña ch©n vÞt cho phÐp ®¹t ®îc
hiÖu suÊt chung cña H§L cao vµ khai th¸c hÕt c«ng suÊt ®éng c¬. HiÖu suÊt
chung cña H§L ®îc tÝnh: ηH§L= η0.ηP.ηt®
Trong ®ã: η0: HiÖu suÊt chung cña ®éng c¬.
ηP: HiÖu suÊt ch©n vÞt.
ηt®: HiÖu suÊt truyÒn ®éng. Tuú theo c¸c thiÕt bÞ l¾p ®Æt trªn hÖ trôc
(Nh bé li hîp, hép gim tèc, c¸c gèi ®ì ®êng trôc) mµ ta cã : ηt® = ηlh.ηgt.ηtr NÕu
xem ηt®
= const trong qu¸ tr×nh khai th¸c th×: ηH§L= η0.ηP
Hay: (32)
Trong ®ã: QH: NhiÖt trÞ thÊp cña nhiªn liÖu.
VP: Tèc ®é tiÕn thùc cña ch©n vÞt.
ge: SuÊt tiªu hao nhiªn liÖu cã Ých.
NS: C«ng suÊt trªn ®Õ ch©n vÞt.
T: Lùc ®Èy ch©n vÞt
S
P
He
HDL
N
VT
Qg .75
.
.
.
3,632
=
η
2
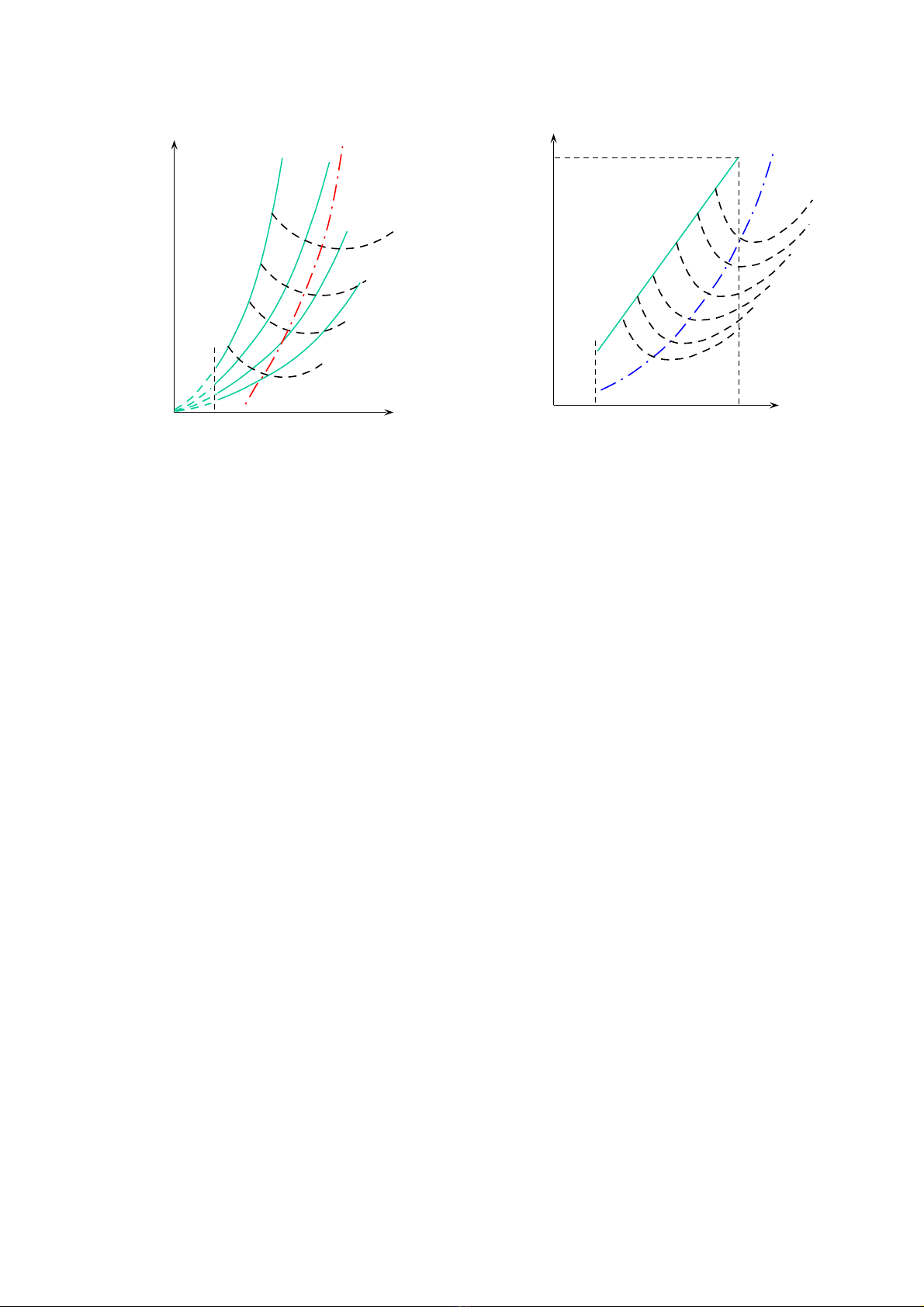
Trong thùc tÕ viÖc x¸c ®Þnh T, VP, NS gÆp nhiÒu khã kh¨n nªn cã thÓ dùa vµo
hai ®êng cong hiÖu suÊt ch©n vÞt vµ ®éng c¬.
NS
0 nmin nS
H/Dmin
H/Dmax
H/Dn
VS = const
ηP
max
H×nh 3.1. BiÓu diÔn ®êng hiÖu
s uÊt lín nhÊt cña ch©n vÞt.
η
P
max: §êng hiÖu s uÊt ch©n vÞt lín
nhÊt.
§êng hiÖu suÊt cña ch©n vÞt ®¹t
gi¸ trÞ lín nhÊt khi c«ng suÊt ph¸t ra
cña ®éng c¬ lµ nhá nhÊt trªn cïng
mét tèc ®é tµu.
N
η
P
max = f(H/D, n) Khi N=Nmin
V=cons t
ge = const
Ne
Nn
0 nmin nn n
η0max
Mn = const
H×nh 3.2. BiÓu diÔn ®êng hiÖu s uÊt
lín nhÊt cña ®éng c¬.
η
0
max: §êng hiÖu s uÊt ch©n vÞt lín
nhÊt.
§êng hiÖu suÊt lín nhÊt cña ®éng c¬
lµ ®êng nèi c¸c ®iÓm trªn ®êng suÊt
tiªu hao nhiªn liÖu cã Ých kh«ng ®æi
nhng cã c«ng suÊt ph¸t ra lµ nhá nhÊt.
N
η
0
max=(Nen/ nn
2).n2
3
3.1.2. PhƯ¬ng ph¸p ®¬n gi¶n x¸c ®Þnh ®Ưêng cong (h/d - n)
tèi Ưu.
B»ng c¸ch sö dông c¸c thiÕt bÞ ®o ta ®o ®ưîc c«ng suÊt trªn trôc ch©n vÞt theo c¸c
d·i vßng quay ®éng c¬ hoÆc ch©n vÞt ë c¸c tû sè bưíc kh¸c nhau. Qua ®ã chän ®-
ưîc gi¸ trÞ c«ng suÊt vµ vßng quay cho ta cho ta gi¸ trÞ vËn tèc tµu lµ lín nhÊt.
Hay nãi c¸ch kh¸c: t¹i mét gi¸ trÞ vËn tèc tµu kh«ng ®æi ta cã thÓ chän ®ưîc mét gi¸
trÞ c«ng suÊt nhá nhÊt (NS)min. Khi ®ã hÖ sè m«men (KM) sÏ ®¹t gi¸ trÞ tèi ưu (KM
=KMT.u) vµ ®ưîc tÝnh:
Trong ®ã:NS : C«ng suÊt ®o ®ưîc trªn trôc ch©n vÞt (ml).
n: Vßng quay trôc ch©n vÞt (v/p).
D: ®ưêng kÝnh ch©n vÞt (m)
ρ: ®é nhít ®éng lùc häc cña nưíc biÓn. ρ =104,5 (KG.s2/m3)
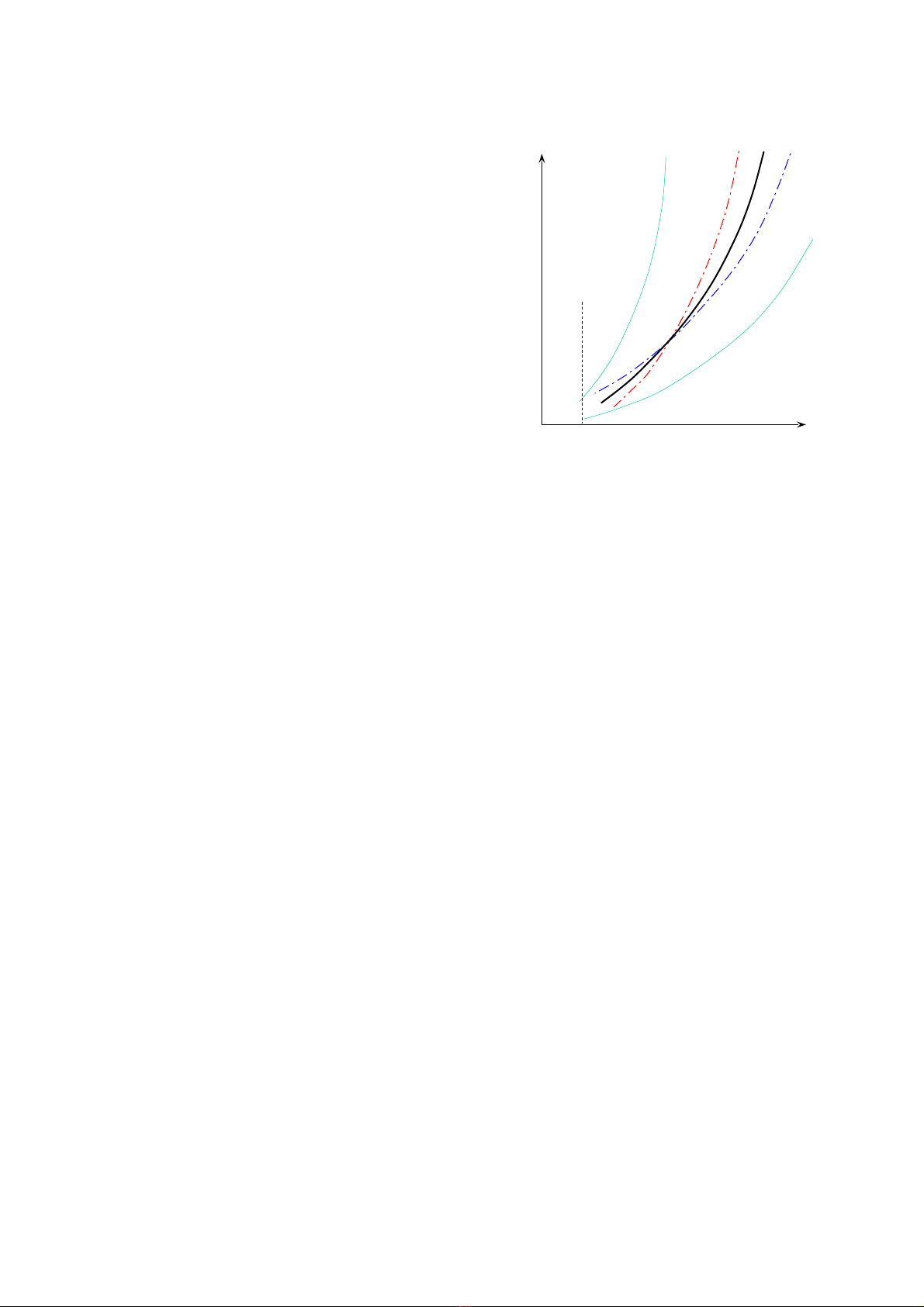
ηP
max
η0
max
ηH§L
max
H×nh 3.3. BiÓu diÔn c¸ch x¸c ®Þnh
®êng hiÖu s uÊt lín nhÊt cña H§L
lai ch©n vÞt biÕn bíc.
η
P
max: §êng hiÖu s uÊt lín nhÊt cña
ch©n vÞt.
η
0
max: §êng hiÖu s uÊt lín nhÊt cña
®éng c¬.
η
H§L
max: §êng hiÖu s uÊt chung lín
nhÊt cña H§L.
§êng hiÖu suÊt chung lín nhÊt cña
H§L lµ trung b×nh nh©n cña ηP
max vµ
η0
max.
η
H§L
max =
η
P
max.
η
0
max
Sai sè cña ph¬ng ph¸p nµy tõ 1-3%.
NS
0 nmin nS
(H/D)max
(H/D)min
x¸c ®Þnh ®"êng hiÖu s uÊt lín nhÊt cña H§L lai ch©n vÞt biÕn b"íc b»ng ph"
¬ng ph¸p ®å thÞ
Khi ®iÒu kiÖn khai th¸c thay ®æi th× ®êng η0
max sÏ bÞ dÞch chuyÓn. NÕu ®iÒu
kiÖn khai th¸c khã kh¨n h¬n th× η0
max sÏ dÞch sang phi vµ ngîc l¹i.
Do vËy trong qu¸ tr×nh khai th¸c ta phi thay ®æi tû sè (H/D) vµ tay ga nhiªn liÖu
®Ó sao cho ®iÓm phèi hîp c«ng t¸c lu«n n»m trªn ®êng cong (H/D - n) tèi u.
4
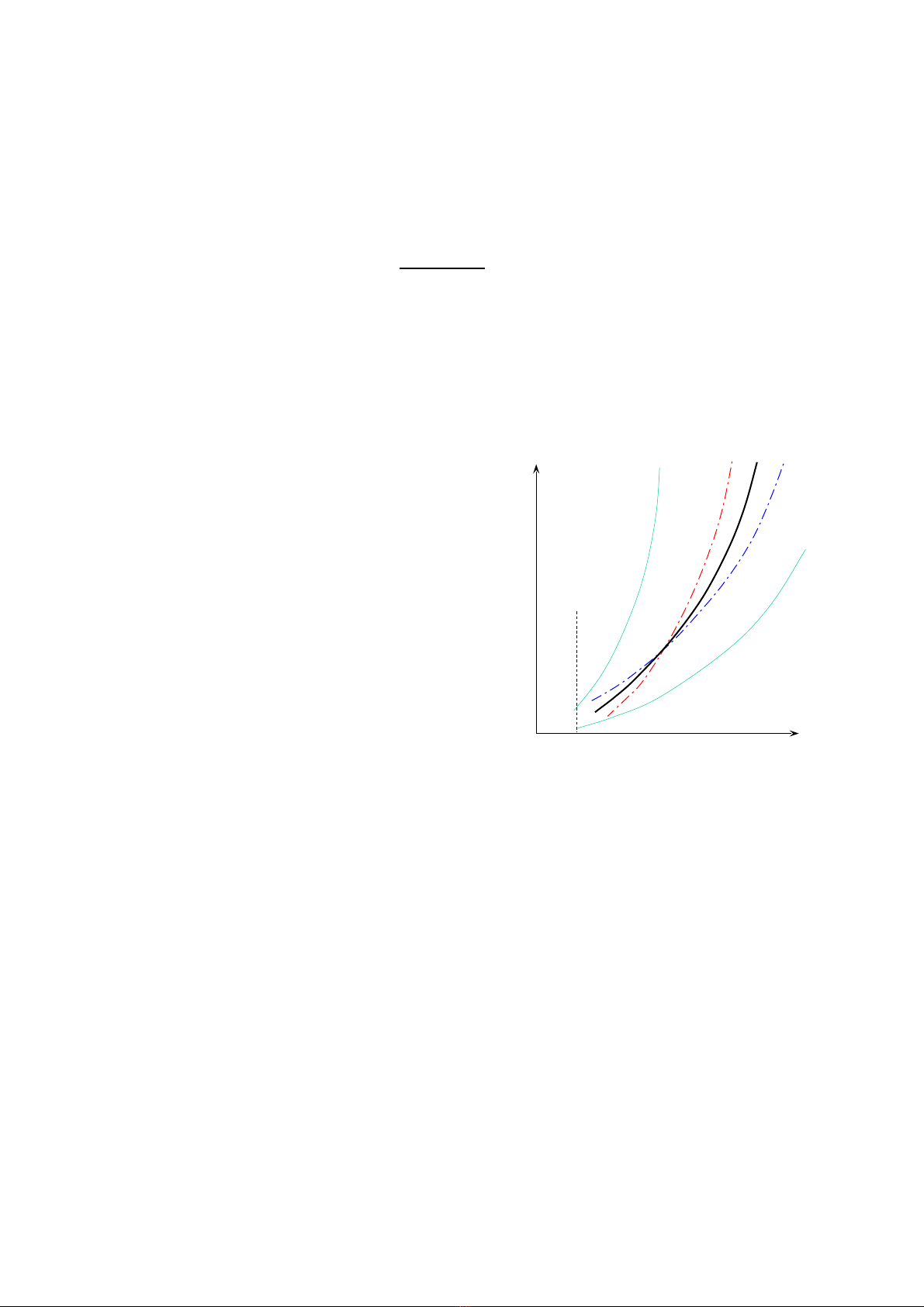
HoÆc theo c«ng thøc thùc nghiÖm: KMT.u = 0,07.(S0/ S)
C«ng thøc trªn ®óng khi: 0,26
≤
dP/D
≤
0,31
Trong ®ã:dS : §ưêng kÝnh may-¬ ch©n vÞt.
S0 : DiÖn tÝch thùc cña c¸nh ch©n vÞt.
S: DiÖn tÝch h×nh chiÕu cña ch©n vÞt.
Khi ®ã ®ưêng cong hiÖu suÊt ch©n vÞt sÏ ®ưîc x¸c ®Þnh theo hµm sau:
Tõ hµm trªn cho tríc c¸c gi¸ trÞ vßng
quay ta tÝnh ®îc c«ng suÊt t¬ng
øng. C¸c cÆp gi¸ trÞ (N - n) cho phÐp
ta x©y dùng ®êng hiÖu suÊt lín nhÊt
cña ch©n vÞt.
KÕt hîp víi ®êng cong hiÖu suÊt lín
nhÊt cña ®éng c¬:
N
η
0
max=(Nen/ nn
2).n2
ta sÏ x©y dùng ®îc ®êng cong hiÖu
suÊt chung lín nhÊt cña H§L.
Ph"¬ng ph¸p ®¬n gi¶n x¸c ®Þnh ®"êng cong (H/D – n) tèi "u
ηP
max
η0
max
ηH§L
max
NS
0 nmin nS
(H/D)max
(H/D)min
H×nh 3.4. Minh häa c¸ch x¸c ®Þnh ®êng
cong hiÖu s uÊt chung lín nhÊt cña H§L.
5
3
5
.
24000
.
max
n
DK
N
MTu
P
=
η