
Lý Thuyết Đàn Hồi
21
Chương II
LÝ THUYẾT ỨNG SUẤT
§2.1 Phân loại các lực
Khi các lực từ bên ngoài tác dụng lên vật thể thì bên trong chúng xuất hiện các lực tương tác giữa
các phần của vật thể với nhau. Theo quan điểm của cơ học các môi trường liên tục, các lực bên trong này
phân bố liên tục trong lòng vật thể.
Trong nghiên cứu, để cho tiện lợi, người ta phân các lực ra thành hai nhóm chính: Lực khối và
Lực mặt .
2.1.1. Lực khối
Lực khối là lực tác dụng lên mỗi thể tích phân tố của vật thể.
Lực khối phân tố, tác dụng lên thể tích vô cùng bé dV có độ lớn tỉ lệ với thể tích này và được xác
định bằng biểu thức dVF, trong đó
F
là một véctơ hữu hạn, biểu thị lực khối tác dụng lên một đơn vị thể
tích, được gọi là lực khối đơn vị. Lực khối đơn vị là hàm của toạ độ các điểm.
Lực khối, tác dụng lên toàn vật thể, được định nghĩa như là hợp lực của các lực khối phân tố của
toàn vật thể và được tính bằng tích phân trên toàn thể tích vật thể.
∫∫∫
=
V
B
dVFF
(2.1)
Cơ sở của khái niệm về lực khối đưa ra trên đây trên sơ sở của giả thiết về tính liên tục của vật thể
khảo sát.
Lực trọng trường, lực quán tính, vv… là những ví dụ về các lực khối. Hình H2.1 biểu diễn lực khối
là trọng lượng bản thân của một vật thể.
Về sau, ta ký hiệu hình chiếu của vectơ
F
lên các trục toạ độ Ox, Oy, Oz trong một hệ toạ độ Đề-
Các (De Cartre) gắn vào vật thể, tương ứng, là F
x
, F
y,
F
z ;
X, Y, Z hoặc B
x
B
y
, B
z
.
2.1.2. Lực mặt
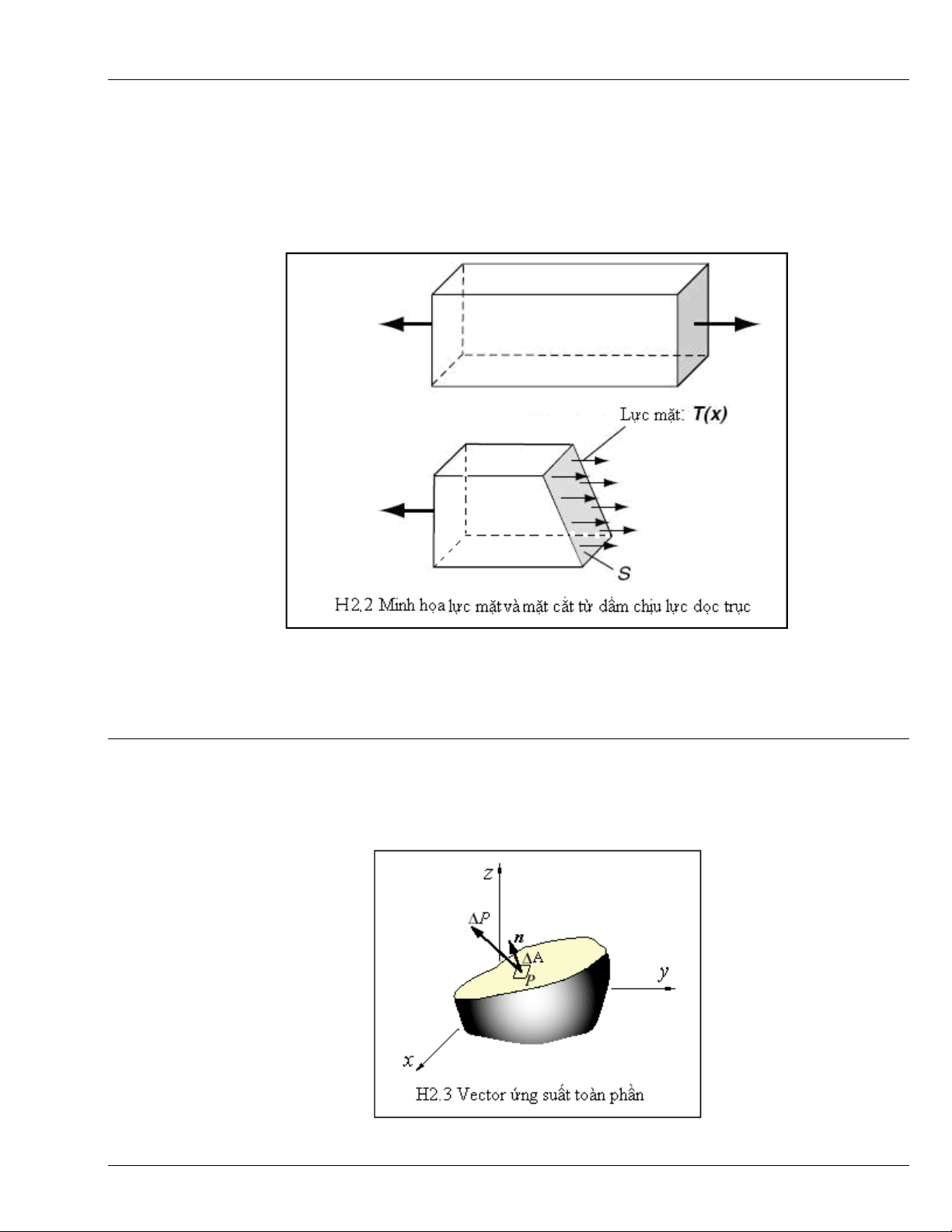
Lực mặt là lực tác dụng lên bề mặt giới hạn không gian bị chiếm chỗ bởi vật thể khảo sát và là kết
quả tương tác vật lý giữa vật thể khảo sát với vật thể khác.
Hình H2.2 biểu diễn lực mặt tác dụng lên mặt cắt tưởng tượng, cắt dầm khảo sát ra làm hai phần.
Lực mặt phân tố tác dụng lên bề mặt vô cùng bé dS được xác định bằng biểu thức
(
)
dSx
n
T
, trong
đó,
(
)
x
n
T
là vector hữu hạn và chính là lực mặt tác dụng lên một đơn vị diện tích của phân tố bề mặt
Vectơ
(
)
x
n
T
được gọi là ứng suất toàn phần hay lực mặt đơn vị (trên mặt có phấp tuyến ngoài n).
Lý Thuyết Đàn Hồi
22
Cũng như trước đây đối với lực khối, lực mặt được định nghĩa như là hợp lực của tất cả các lực
mặt phân tố tác dụng lên bề mặt khảo sát và được tính bằng cách tích phân các lực mặt phân tố trên toàn
diện tích tác dụng:
(
)
∫∫
=
S
n
S
dSxTF
(2.2)
Lực mặt có thể là ngoại lực tác dụng lên bề mặt bao quanh vật thể, cũng có thể là nội lực tác dụng qua lại
giữa các của phần vật thể khi chúng bị “tách” khỏi nhau bởi các mặt cắt nào đó. Trong trường hợp này,
lực mặt có vai trò thay cho tác dụng từ phần vật thể bị cắt bỏ lên phần vật thể khảo sát
§2.2. Vector lực mặt đơn vị và tensor ứng suất
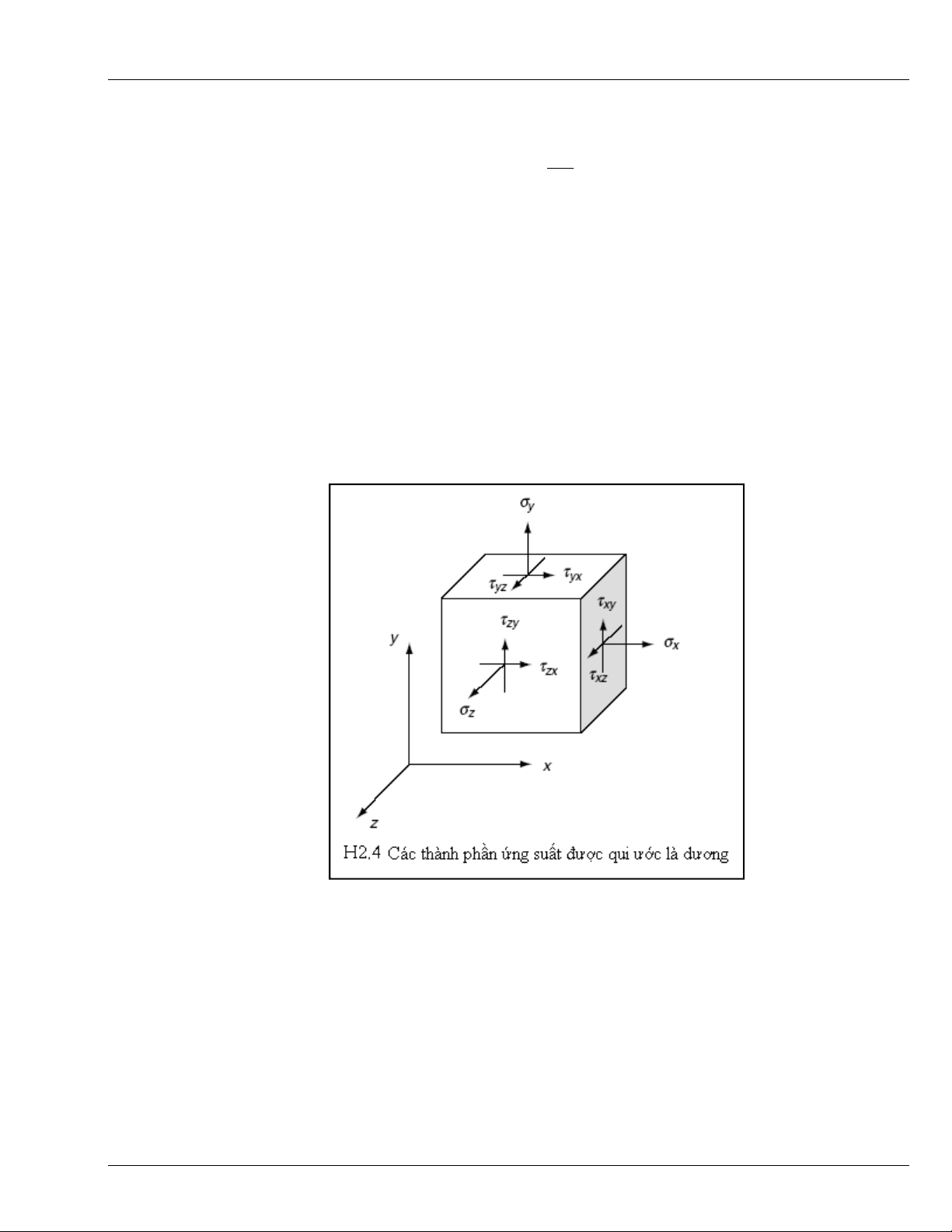
Để xác định sự phân bố của các nội lực tác dụng bên trong các môi trường liên tục, hãy xét một vật
thể bất kỳ chịu tác dụng của các lực ngoài (tập trung hoặc/và phân bố) tùy ý. Ta thực hiện một mặt cắt như
biểu thị trên hình vẽ H2.3.
Lý Thuyết Đàn Hồi
23
Trên mặt cắt, xét một phân tố diện tích vô cùng bé
A
∆
, với pháp tuyến ngoài n. Hợp lực các lực
mặt tác dụng lên
A
∆
được ký hiệu bởi
P
∆
. Trên diện tích vô cùng bé này, không để ý đến bất kỳ ngẫu
lực nào. Vector lực mặt đơn vị, hay còn gọi là vector ứng suất toàn phần, được định nghĩa bởi.
(
((
( )
))
)
A
x
A
∆
∆
∆
P
nT
n
0
lim,
→
→→
→
=
==
=
(2.3)
Ký hiệu x chỉ vị trí của phân tố bề mặt khảo sát.
Lực mặt đơn vị phụ thuộc vào cả vào vị trí trong không gian của phân tố diện tích khảo sát lẫn
vector pháp tuyến ngoài của phân tố diện tích nói trên. Như vậy là cho dù khảo sát ngay tại một điểm
nhưng khi thay đổi phương hướng mặt cắt đi qua điểm này, vector lực mặt đơn vị cũng thay đổi (cả về trị
số lẫn phương, chiều).
Trên cơ sở của nguyên lý Newton về tác dụng - phản tác dụng, ta có
(
((
(
)
))
)
(
((
(
)
))
)
xx
nn
n,Tn,T −
−−
−−
−−
−=
==
= (2.4)
Bây giờ ta xét một trường hợp đặc biệt khi mà phân tố diện tích
A
∆
trùng với mỗi một trong 3 mặt
phẳng tọa độ, tức khi mà vector đơn vị pháp tuyến ngoài của diện tích trùng với hướng dương của trục toạ
độ tương ứng.
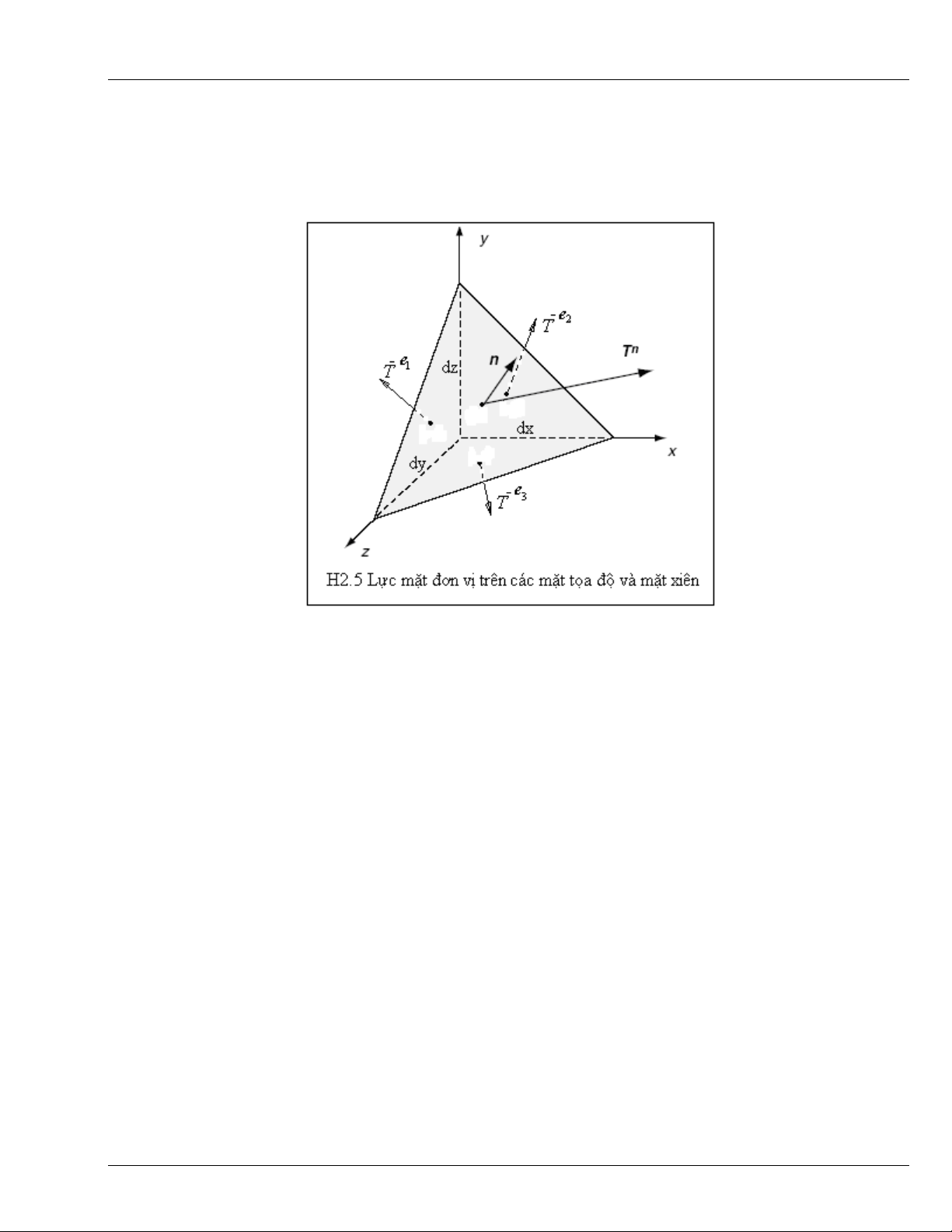
Hình H2.4 là minh họa cho trường hợp này, trong đó, phân tố diện tích
A
∆
chính là mặt bên của
hình hộp phân tố tách ra từ vật thể khảo sát.
Khi đó, lực mặt đơn vị (còn gọi là ứng suất toàn phần) trên từng mặt, song song với các mặt tọa
độ, được xác định theo các công thức sau:
(
((
(
)
))
)
(
((
( )
))
)
(
((
( )
))
)
3213
3212
3211
eeeenT
eeeenT
eeeenT
n
n
n
zzyyzx
yzyyx
xzxyx
σττ
τστ
ττσ
+
++
++
++
+=
==
==
==
=
+
++
++
++
+=
==
==
==
=
+
++
++
++
+=
==
==
==
=
(2.5)
Trong đó,
321
,, eee là các vector đơn vị trên các trục tọa độ, còn 9 đại lượng
{
}
zxxzzyyzyxxyxyx
ττττττσσσ
,,,,,,,,
là các thành phần của lực mặt đơn vị (tức của ứng suất toàn phần) trên mỗi một trong 3 mặt toạ độ, như
minh họa trên hình H2.4, cụ thể:
•
xzxyx
ττσ
,,
là các thành phần của lực mặt đơn vị trên mặt tọa độ x,
(
((
(
)
))
)
1
enT
n
=
==
=;

Lý Thuyết Đàn Hồi
24
•
yzyxy
ττσ
,,
là các thành phần của lực mặt đơn vị trên mặt tọa độ y,
(
((
(
)
))
)
2
enT
n
=
==
=;
•
zxzyz
ττσ
,,
là các thành phần của lực mặt đơn vị trên mặt tọa độ z,
(
((
(
)
))
)
3
enT
n
=
==
=
;
Các đại lượng
{
}
zxxzzyyzyxxyxyx
ττττττσσσ
,,,,,,,,
này được gọi là các thành phần ứng suất.
Khi biến đổi (xoay) hệ tọa độ, các thành phần ứng suất tại một điểm cũng thay đổi theo. Sự thay đổi này
phản ảnh trạng thái ứng suất tại một điểm (chứ không làm thay đổi trạng thái này).
Các thành phần ứng suất,
ij
σ
có thể biểu diễn dưới dạng ma trận như sau:
[
[[
[ ]
]]
]
=
==
==
==
=
zzyzx
yzyyx
xzxyx
σττ
τστ
ττσ
σ
σ
(2.6)
Và cũng có thể biểu diễn dưới dạng một tenso hạng hai,
ij
σ
, tuân thủ qui luật tổng quát chuyển hệ tọa độ
đối với các thành phần của một tensor.
Các thành phần ứng suất
{
}
zyx
σσσ
,,
chính là thành phần của vector ứng suất toàn phần trên các
pháp tuyến ngoài của mặt chịu tác dụng, và được gọi là ứng suất pháp, còn các thành phần ứng suất còn
lại,
{
}
zxxzzyyzyxxy
ττττττ
,,,,,
, nằm trong các mặt phẳng tiếp tuyến với mặt chịu lực, được gọi là các ứng
suất tiếp hay ứng suất cắt.
Qui tắc xác định dấu của các thành phần ứng suất:
Không phụ thuộc gì vào các trục tọa độ, các ứng suất pháp sẽ là dương khi có tác dụng kéo, âm khi
nén (từ ngoài vào bên trong vật thể) và với chúng, chỉ cần sử dụng một chỉ số dưới biểu thị pháp tuyến
ngoài của bề mặt tác dụng để phân biệt vì mỗi một bề mặt chỉ có một pháp tuyến ngoài. Trong khi đó, trên
mỗi bề mặt vuông góc với một trục tọa độ có hai thành phần ứng suất tiếp, theo phương hai trục tọa độ
còn lại. Các ứng suất cắt trong trường hợp này cần đến hai chỉ số dưới để phân biệt: chỉ số trước cho biết
trục tọa độ vuông góc với bề mặt chịu tác dụng còn chỉ số sau biểu thị phương tác dụng của ứng suất này
và qui ước về dấu của các ứng suất cắt này như sau: trên bề mặt có pháp tuyến ngoài trùng với hướng
dương của một trục tọa độ nào đó thì ứng suất cắt sẽ dương nếu như nó theo hướng dương của trục tọa độ
tương ứng và ngược lại. Không có qui ước dấu cho ứng suất tiếp toàn phần (bằng tổng hợp của hai thành
phần ứng suất tiếp theo hai trục tọa độ tương ứng). Qui tắc đơn giản trên đây về dấu của các thành phần
ứng suất cần phải được nắm vững.
Trên hình vẽ H2.4 biểu diễn các thành phần ứng suất được qui ước là dương (trên các mặt có pháp
tuyến ngoài trùng với hướng dương của các trục tọa độ).
Các khái niệm tensor ứng suất và lực mặt đơn vị trên đây được đưa ra dựa trên nguyên lý biến
dạng bé, theo đó, không để ý đến sự sai khác giữa cấu hình biến dạng và không biến dạng của vật thể (cấu
hình không biến dạng được dùng làm cấu hình qui chiếu). Sự sai khác nói trên là nhỏ, thường được bỏ qua
và chỉ xét đến khi nghiên cứu các hiệu ứng cấp cao. Tuy nhiên, trong lý thuyết biến dạng lớn, sự sai khác
về kích cỡ giữa hai cấu hình biến dạng và không biến dạng này lại là chủ đề chính, là cơ sở của việc việc
hình thành các bài toán tương ứng. Chính việc xét đến sự sai khác này làm nảy sinh ra một khái niệm ứng
suất bổ sung, gọi là tensor ứng suất Piola-Kirchhoff, biểu thị lực trên đơn vị diện tích của cấu hình qui
chiếu. Trong một sơ đồ tổng quát hơn, ứng suất được biểu diễn bởi tensor ứng suất Cauchy. Tuy nhiên,
trong giáo trình này, ta chỉ sử dụng nguyên lý biến dạng bé và do đó, không cần thiết phải nói đến sự
khác biệt giữa các khái niệm ứng suất nói trên.
Tiếp đến, hãy khảo sát cân bằng của một tứ diện phân tố có các cạnh dx, dy, dz dưới tác dụng của
các lực mặt trên các mặt tọa độ và mặt xiên (H2.5). Lực khối được bỏ qua vì là vô cùng bé bậc cao hơn
các lực mặt. Có thể biểu diễn vector đơn vị pháp tuyến ngoài
n
của mặt xiên này theo các vector đơn vị
cơ bản của hệ trục tọa độ nhờ biểu thức sau
321
eeen
zyx
nnn ++=
, (2.7)
Lý Thuyết Đàn Hồi
25
trong đó,
zyx
nnn ,,
là các cosine chỉ phương của vector đơn vị pháp tuyến ngoài
n
trong hệ tọa độ cho
trước còn
321
,, eee là các vector đơn vị trên các trục tọa độ của hệ này.
Sử dụng điều kiện hợp lực của tất cả các lực tác dụng lên tứ diện phân tố phải triệt tiêu (với lực
khối được bỏ qua), ta thu được phương trình:
(
((
(
)
))
)
(
((
(
)
))
)
(
((
(
)
))
)
0
321
=
==
=−
−−
−=
==
=+
++
+−
−−
−=
==
=+
++
+−
−−
−=
==
=+
++
+eTeTeTT nnnnnn
zyx
n
Từ đó, liên hệ với (2.4), có:
(
)
(
)
(
)
321
eTeTeTT =+=+== nnnnnn
zyx
n
(2.8)
Sử dụng tiếp quan hệ (2.5), thu được
(
)
( )
( )
3
2
1
.
.
.
e
e
eT
xzzyzyxz
zzyyyxxy
zzxyyxxx
n
nnn
nnn
nnn
σττ
τστ
ττσ
+++
+++
++=
. (2.9)
Hay có th
ể
vi
ế
t g
ọ
n theo ký hi
ệ
u ch
ỉ
s
ố
(ký hi
ệ
u tensor)
jji
n
i
n
σT= (2.10)
Dạng vô hướng của phương trình (2.9) là:
zzyyzxxz
n
z
zzyyyxxy
n
y
zzxyyxxx
n
x
nnnT
nnnT
nnnT
σττ
τστ
ττσ
+
++
++
++
+=
==
=
+
++
++
++
+=
==
=
+
++
++
++
+=
==
=
(2.9*)
với n
z
n
y
n
x
TTT ,,
là các thành phần của lực trên mặt xiên
n
T
theo các trục tọa độ Ox, Oy, Oz (Trong một số
công thức, các thành phần này có thể được ký hiệu bởi
ννν
ZYX ,, ).
Phương trình (2.9)/(2.9*), biểu thị quan hệ giữa các ứng suất toàn phần trên mặt xiên và các mặt
tọa độ của tứ diện phân tố, được gọi là phương trình điều kiện biên. Về thực chất, phương trình điều kiện
biên đúng cho cả phân tố trên mặt biên lẫn phân tố trong lòng vật thể khảo sát.
Các thành phần của vector ứng suất toàn phần trên các trục tọa độ Ox, Oy, Oz của bề mặt có pháp
truyến ngoài n còn được ký hiệu bởi
nnn
ZYX ,, .






















![Bài tập tối ưu trong gia công cắt gọt [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251129/dinhd8055/135x160/26351764558606.jpg)













