Lý Thuyết Đàn Hồi
82
Chương VI
BÀI TOÁN PHẲNG
Như đã được nhắc đến, cho tới nay vẫn chưa tìm được lời giải trực tiếp của bài toán đàn hồi cho trường
hợp tổng quát, vì thế cho nên, lời giải trong các trường hợp riêng có một giá trị hết sức to lớn. Các lời giải
trong các trường hợp này có được nhờ hạn chế bớt, bằng một cách nào đó, tính tổng quát của bài toán
được đặt ra. Việc biến đổi gần đúng bài toán ba chiều (3D) về bài toán hai chiều (2D), dẫn đến việc hình
thành các bài toán phẳng, là một ví dụ. Đây là một loại bài toán mà lời giải của nó có ứng dụng thực tế
rộng rãi.
§6.1 Thiết lập bài toán phẳng
Bài toán phẳng của Lý thuyết đàn hồi có thể phân thành hai nhóm: các bài toán về biến dạng
phẳng và các bài toán về ứng suất phẳng. Trước khi tiến hành giải bài toán, ta hãy xác định các phương
trình cơ bản cùng với các công thức thiết yếu của hai bài toán nói trên, cho vật thể trực hướng.
6.1.1 Trạng thái biến dạng phẳng.
Khái niệm biến dạng phẳng dùng để chỉ một trạng thái của vật thể, mà theo đó, một trong các
chuyển vị bằng 0 còn hai chuyển vị còn lại không phụ thuộc vào toạ độ tương ứng với chuyển vị bằng 0
nói trên. Trục tương ứng với thành phần cv bằng 0, giả sử, là z. Giả thiết thêm rằng, mặt phẳng x-y là mặt
phẳng đàn hồi đối xứng. Định nghĩa của trạng thái biến dạng phẳng có thể được biểu diễn như sau:
(
)
(
)
yxvvyxuuw ,;,;0
=
=
=
. (6.1)
Trên cơ sở của quan hệ biến dạng - chuyển vị (5.2) và định luật Hooke tổng quát (4.31), từ (6.1) có thể
suy ra:
(
)
(
)
(
)
.0;,;,;, ======
zxyzzxyxyyyxx
yxyxyx
γγεγγεεεε
. (6.2)
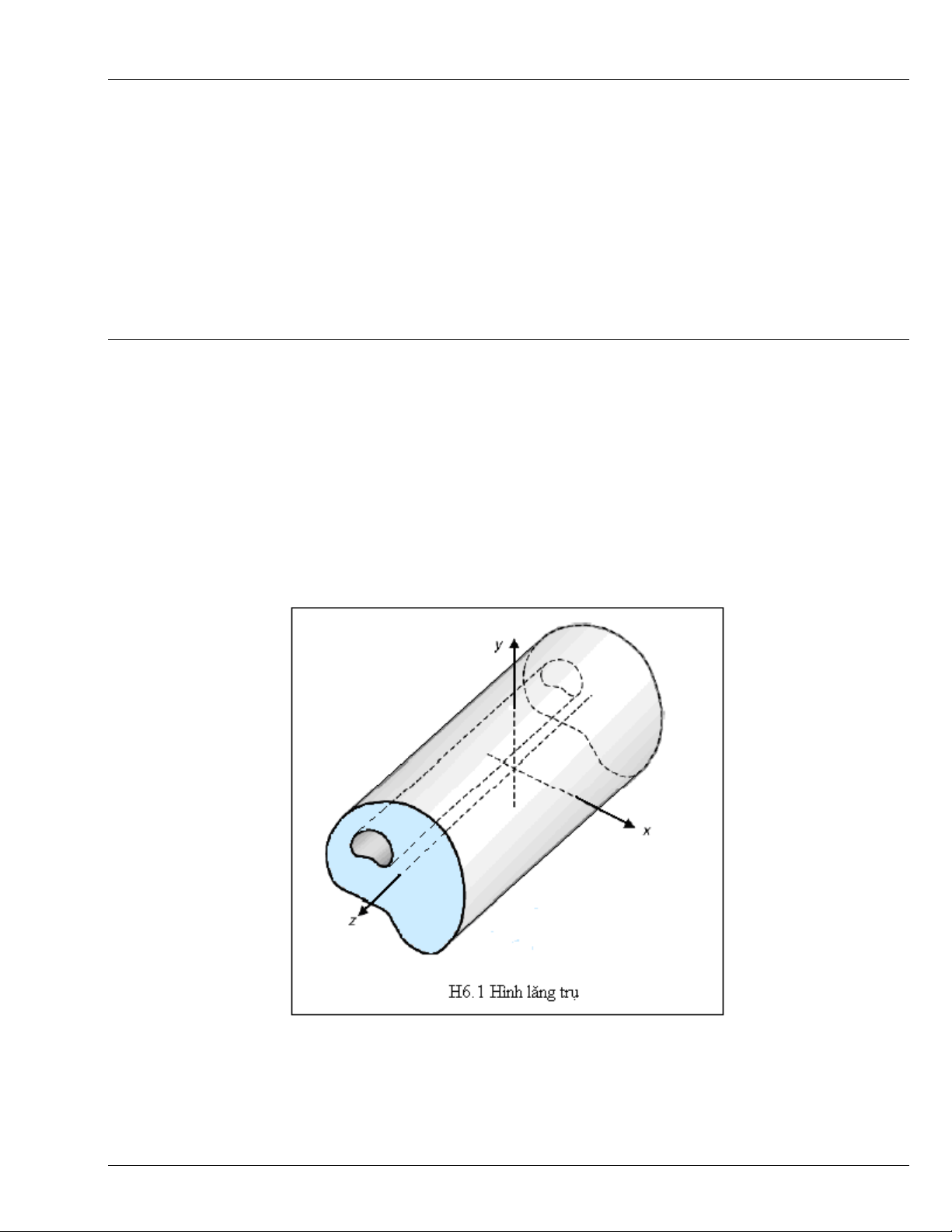
Trạng thái biến dạng phẳng xảy ra trong vật thể hình lăng trụ dài, chịu tải trọng tác dụng vuông góc với
trục của lăng trụ và không đổi dọc theo trục này (H6.1). Có thể nhận thấy rằng các tiết điện ngang R của
Lý Thuyết Đàn Hồi
83
hình lăng trụ trên chuyển vị giống hệt nhau và như vậy, bài toán 3D có thể đưa về 2D, xác lập trong miền
R (mặt phẳng x-y).
Dựa trên các điều kiện (6.1) và (6.2), có thể thu được các phương trình cơ sở và các công thức chủ yếu
của bài toán đàn hồi như sau:
1. Phương trình cân bằng:
Phương trình cân bằng (5.1) trong trường hợp khảo sát có thể viết:
;0 ;0 =
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
yxyx
yxyxy
x
σ
τ
τ
σ
(6.3)
(Phương trình thứ 3 dẫn đến sự đồng nhất 0 = 0 giữa hai vế; Lực khối được bỏ qua:
0===
zyx
FFF
)
2. Quan hệ biến dạng-cv (5.2) sẽ có dạng:
.0;
;0;;
==
∂
∂
+
∂
∂
=
=
∂
∂
=
∂
∂
=
zxyzxy
zyx
y
u
x
v
y
v
x
u
γγγ
εεε
(6.4)
3. Phương trình tương thích:
Từ (5.3) và (6.2), có:
.
2
2
2
2
2
yx
xy
xyy
x
∂∂
∂
=
∂
∂
+
∂
∂
γε
ε
(6.5)
4. Định luật Hooke:
a. Cho vật thể trực hướng:
Để có được công thức của định luật Hooke cho vật thể trực hướng trong trường hợp khảo sát, có thể xuất
phát từ công thức (4.31), được kết quả:
( )
( )
.0;
1
;11
;11
====
−−−=
−−−=
zxyzzxy
xy
xy
xy
xzzy
xy
x
x
yzzy
y
y
y
yx
yZzx
yx
y
y
xzzx
x
x
x
G
EE
EE
γγετγ
ν
νν
ν
σ
νν
σ
ε
ν
νν
ν
σ
νν
σ
ε
(6.6)
b. Cho vật thể đẳng hướng:
Trường hợp vặt thể đẳng hướng, cũng tiến hành như trên, nhưng từ công thức (4.40):
.0;
1
;
1
1
;
1
1
2
2
====
−
−
−
=
−
−
−
=
zxyzzxyxy
yxx
yxx
G
E
E
γγετγ
σ
ν
ν
σ
ν
ε
σ
ν
ν
σ
ν
ε
(6.7)
Ngoài ra, từ công thức (4.41) ta có quan hệ đảo của (6.7):
Lý Thuyết Đàn Hồi
84
( ) ( )
.0;
21
2
;0;
21
1
21
2
;
2
1
2;
2121
1
2
=+=+
−
=
=
−
−
+
−
=
=
−
+
−
−
=
zxyxyxz
yzyxy
xyxyyxx
G
G
GG
τεελεε
ν
ν
σ
τε
ν
ν
ε
ν
ν
σ
γτε
ν
ν
ε
ν
ν
σ
(6.8)
5.
Qui lu
ậ
t bi
ế
n
đổ
i các thành ph
ầ
n
ứ
ng su
ấ
t và các thành ph
ầ
n bi
ế
n d
ạ
ng khi xoay h
ệ
to
ạ
độ
:
Trên c
ơ
s
ở
các công th
ứ
c (2.21) và (3.22) (6.2) có các công th
ứ
c bi
ế
n
đổ
i thành ph
ầ
n
ứ
ng su
ấ
t và
thành ph
ầ
n bi
ế
n d
ạ
ng s
ẽ
nh
ư
sau (H6.2): (v
ớ
i
θ
θ
θ
θ
cos ,sin ,sin ,cos
2211
=
−
=
=
=
mlml
)
( )
;2cos2sin
1
;2sincossin
;2sinsincos
''
22
'
22
'
θτθσστ
θτθσθσσ
θτθσθσσ
xyxyyx
xyyxy
xyyxx
+−=
−+=
++=
(6.9)
( )
.2cos2sin
1
;2sin
2
1
cossin
;2sin
2
1
sincos
''
22
'
22
'
θγθεεγ
θγθεθεε
θγθεθεε
xyxyyx
xyyxy
xyyxx
+−=
−+=
++=
(6.10)
6.
Công th
ứ
c th
ế
n
ă
ng
đơ
n v
ị
cho v
ậ
t li
ệ
u
đẳ
ng h
ướ
ng:
( )
.
1
2
2
1
222
2
+
−
++
−
=
yxxyyx
E
W
σνστ
ν
σσ
ν
(6.11)
7.
Các bi
ế
n d
ạ
ng chính :
( )
,0
;
2
1
2
3
2
2
2,1
=
+−±
+
=
ε
γεε
εε
ε
xyyx
yx
(6.12)
(tr
ụ
c Oz trùng v
ớ
i m
ộ
t trong các tr
ụ
c chính c
ủ
a bi
ế
n d
ạ
ng).
6.1.2 Trạng thái ứng suất phẳng.
Tr
ườ
ng h
ợ
p th
ứ
hai c
ủ
a bài toán
đ
àn h
ồ
i
đượ
c rút g
ọ
n v
ề
2D là bài toán v
ề
tr
ạ
ng thái
ứ
ng su
ấ
t ph
ẳ
ng.
Tr
ạ
ng thái
ứ
ng su
ấ
t
đượ
c g
ọ
i là ph
ẳ
ng khi
ứ
ng su
ấ
t tác d
ụ
ng trên m
ặ
t, vuông góc v
ớ
i m
ộ
t trong các tr
ụ
c
to
ạ
độ
, b
ằ
ng 0,
đồ
ng th
ờ
i, các thành ph
ầ
n
ứ
ng su
ấ
t còn l
ạ
i không ph
ụ
thu
ộ
c vào to
ạ
độ
ứ
ng v
ớ
i tr
ụ
c này.
C
ũ
ng gi
ả
thi
ế
t r
ằ
ng, m
ặ
t ph
ẳ
ng x-y là m
ặ
t ph
ẳ
ng
đ
àn h
ồ
i
đố
i x
ứ
ng.Trên th
ự
c t
ế
, tr
ạ
ng thái
ứ
ng su
ấ
t ph
ẳ
ng
x
ả
y ra trong các t
ấ
m m
ỏ
ng (chi
ề
u dày 2h), ch
ị
u tác d
ụ
ng c
ủ
a các l
ự
c
đặ
t vào vành t
ấ
m, theo ph
ươ
ng song
song v
ớ
i
các m
ặ
t không ch
ị
u l
ự
c
.
Ta ch
ọ
n m
ặ
t ph
ẳ
ng không ch
ị
u l
ự
c (m
ặ
t
đ
á y) làm m
ặ
t t
ọ
a
độ
x-y còn tr
ụ
c z t
ấ
t nhiên là vuông góc v
ớ
i m
ặ
t
t
ọ
a
độ
này. T
ừ
đị
nh ngh
ĩ
a c
ủ
a bài toán, ta có:
(
)
(
)
(
)
.0;,;,;, ======
zxyzzxyxyyyxx
yxyxyx
ττσττσσσσ
(6.13)
Ngoài ra c
ũ
ng có th
ể
k
ế
t lu
ậ
n r
ằ
ng các thành ph
ầ
n chuy
ể
n v
ị
khác 0 c
ũ
ng không ph
ụ
thu
ộ
c vào to
ạ
độ
z
.
Để
th
ỏ
a mãn
đ
i
ề
u ki
ệ
n cácthành ph
ầ
n
ứ
ng su
ấ
t và thành ph
ầ
n chuy
ể
n v
ị
không ph
ụ
thu
ộ
c vào t
ọ
a
độ
z
c
ầ
n
ph
ả
i tri
ệ
t tiêu các thành ph
ầ
n l
ự
c kh
ố
i và l
ự
c m
ặ
t theo ph
ươ
ng
z
. C
ũ
ng có th
ể
cho phép các l
ự
c m
ặ
t và l
ự
c
kh
ố
i này khác 0 khi chúng phân b
ố
đố
i x
ứ
ng qua m
ặ
t ph
ẳ
ng chia
đ
ôi chi
ề
u dày v
ậ
t th
ể
kh
ả
o sát. Tr
ườ
ng
Lý Thuy
ế
t
Đ
àn H
ồ
i
85
h
ợ
p này, v
ớ
i gi
ả
thi
ế
t chi
ề
u dày, 2
h
, bé, có th
ể
s
ử
d
ụ
ng giá tr
ị
trung bình (b
ằ
ng 0) làm c
ơ
s
ở
xác
đị
nh g
ầ
n
đ
úng.
1.
Ph
ươ
ng trình cân b
ằ
ng
:
S
ử
d
ụ
ng (6.14) và tính ch
ấ
t không ph
ụ
thu
ộ
c c
ủ
a các thành ph
ầ
n
ứ
ng su
ấ
t còn l
ạ
i vào to
ạ
độ
z
, t
ừ
ph
ươ
ng
trình cân b
ằ
ng (5.1) ta có k
ế
t qu
ả
:
;0 ;0 =
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
yxyx
yxyxy
x
σ
τ
τ
σ
(6.3)
Đ
ây c
ũ
ng chính là ph
ươ
ng trình cân b
ằ
ng (6.3)
c
ủ
a bài toán bi
ế
n d
ạ
ng ph
ẳ
ng
(v
ớ
i X = Y = Z = 0).
2.
Đị
nh lu
ậ
t Hooke
:
a. Trên c
ơ
s
ở
c
ủ
a
đị
nh lu
ậ
t Hooke cho v
ậ
t li
ệ
u tr
ự
c h
ướ
ng (4.31) và các quan h
ệ
(4.24), ta có:
( )
( )
.0;
1
;
;
1
;
1
xy
===
+−=
−=
−=
zxyzxy
xy
y
y
yz
x
x
xz
z
xyxy
y
y
yxyx
x
x
G
EE
E
E
γγτγ
σ
ν
σ
ν
ε
σνσε
σνσε
(6.14)
b. Trên c
ơ
s
ở
c
ủ
a
đị
nh lu
ậ
t Hooke cho v
ậ
t li
ệ
u
đẳ
ng h
ướ
ng (4.40) và các quan h
ệ
(4.27), ta có:
( )
( )
( ) ( )
.0;
1
;
1
;
1
;
1
===
+
−
−=+=
−=
−=
yzzxxyxy
yxyxz
xyy
yxx
G
E
E
E
γγτγ
σσ
ν
ν
σσ
ν
ε
νσσε
νσσε
(6.15)
3.
Quan h
ệ
bi
ế
n d
ạ
ng - chuy
ể
n v
ị
:
C
ũ
ng v
ớ
i c
ơ
s
ở
trên
đ
ây, có k
ế
t qu
ả
c
ủ
a quan h
ệ
bi
ế
n d
ạ
ng - chuy
ể
n v
ị
trong tr
ườ
ng h
ợ
p kh
ả
o sát:
.0
2
1
;0
2
1
;
2
1
;;;
=
∂
∂
+
∂
∂
=
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
=
∂
∂
=
∂
∂
=
∂
∂
=
x
w
z
u
y
w
z
v
x
v
y
u
z
w
y
v
x
u
zx
yz
xy
zyx
γ
γ
γ
εεε
(6.4)
Quan h
ệ
(6.14) và (6.4) trên
đ
ây
không hoàn toàn gi
ố
ng
v
ớ
i các ph
ươ
ng trình (6.6), (6.7) và (6.4) c
ủ
a
tr
ườ
ng h
ợ
p tr
ạ
ng thái bi
ế
n d
ạ
ng ph
ẳ
ng. Khác bi
ệ
t là
ở
s
ự
có m
ặ
t (khác 0) c
ủ
a thành ph
ầ
n bi
ế
n d
ạ
ng
z
ε
Lý Thuy
ế
t
Đ
àn H
ồ
i
86
trong bài toán tr
ạ
ng thái
ứ
ng su
ấ
t ph
ẳ
ng và
để
cho bài toán là 2D, c
ầ
n ph
ả
i x
ử
lý g
ầ
n
đ
úng nh
ư
trình bày
trong ph
ầ
n d
ướ
i
đ
ây.
4.
Ph
ươ
ng trình t
ươ
ng thích
:
S
ự
có m
ặ
t không mong mu
ố
n c
ủ
a bi
ế
n d
ạ
ng
ε
z
trong bài toán v
ề
tr
ạ
ng thái
ứ
ng su
ấ
t ph
ẳ
ng làm cho các b
ề
m
ặ
t không ch
ị
u l
ự
c
b
ị
vênh chút ít
. Tuy nhiên, v
ớ
i các t
ấ
m m
ỏ
mg,
độ
vênh nói trên là không
đ
áng k
ể
và có
th
ể
b
ỏ
qua. Vì th
ế
cho nên khi l
ấ
y g
ầ
n
đ
úng ε
z
= 0, trên c
ơ
s
ở
ph
ươ
ng trình t
ươ
ng thích
(5.3),
ta có
ph
ươ
ng trình t
ươ
ng thích
trong tr
ạ
ng thái
ứ
ng su
ấ
t ph
ẳ
ng
trùng v
ớ
i
k
ế
t qu
ả
nh
ư
trong tr
ườ
ng h
ợ
p tr
ạ
ng
thái bi
ế
n d
ạ
ng ph
ẳ
ng,
đ
ó là ph
ươ
ng trình:
.
2
2
2
2
2
yx
xy
xyy
x
∂∂
∂
=
∂
∂
+
∂
∂
γε
ε
(6.5)
5.
Qui lu
ậ
t bi
ế
n
đổ
i
các thành ph
ầ
n
ứ
ng su
ấ
t và các thành ph
ầ
n bi
ế
n d
ạ
ng khi xoay h
ệ
to
ạ
độ
:
D
ự
a trên các công th
ứ
c (2.21) và (3.22) ta thu
đượ
c các công th
ứ
c bi
ế
n
đổ
i các thành ph
ầ
n
ứ
ng su
ấ
t, bi
ế
n
d
ạ
ng cho tr
ạ
ng thí
ứ
ng su
ấ
t ph
ẳ
ng. Các công th
ứ
c này c
ũ
ng có d
ạ
ng gi
ố
ng h
ệ
t các công th
ứ
c t
ươ
ng
ư
ng
sc
ủ
a tr
ườ
ng h
ợ
p bi
ế
n d
ạ
ng ph
ẳ
ng.
6.
Th
ế
n
ă
ng bi
ế
n d
ạ
ng
đơ
n v
ị
th
ể
tích
(cho v
ậ
t li
ệ
u
đẳ
ng h
ướ
ng):
(
)
[
]
.22
1
2222
yxxyxyyx
E
W
σστντσσ
−+++=
(6.16)
7
. Các
ứ
ng su
ấ
t chính
trong tr
ạ
ng thái
ứ
ng su
ấ
t ph
ẳ
ng có th
ể
xác
đị
nh theo các công th
ứ
c
( )
.0
;4
2
1
2
3
2
2
2,1
=
+−±
+
=
σ
τσσ
σσ
σ
xyyx
yx
(6.17)
(tr
ụ
c Oz trùng v
ớ
i m
ộ
t trong các tr
ụ
c
ứ
ng su
ấ
t chính)
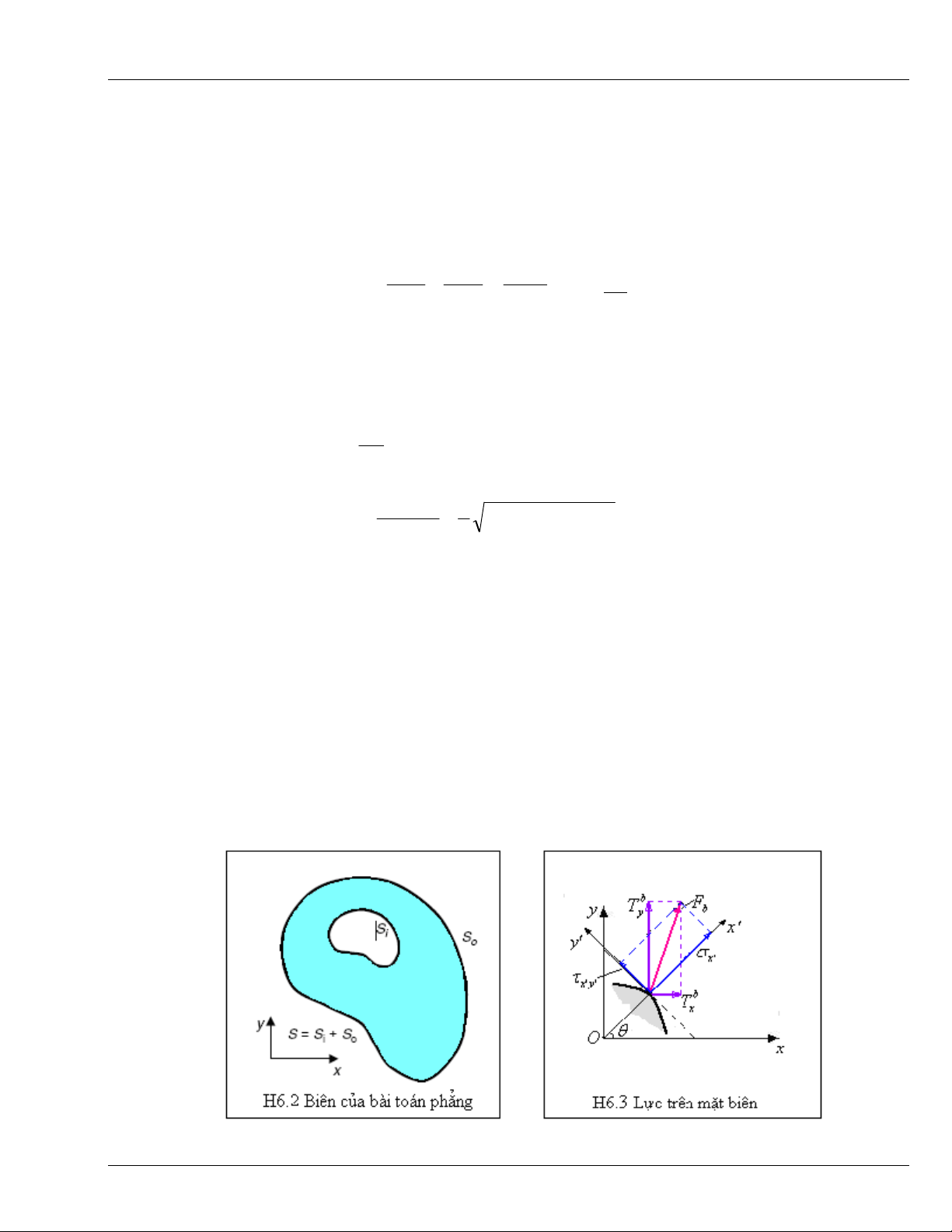
6.1.3 Các điều kiện biên
Đ
i
ề
u ki
ệ
n biên c
ủ
a c
ả
hai bài toán
ứ
ng su
ấ
t ph
ẳ
ng và bi
ế
n d
ạ
ng ph
ẳ
ng là gi
ố
ng h
ệ
t nhau,
đ
ó là
đ
i
ề
u
ki
ệ
n cho tr
ướ
c l
ự
c và/ho
ặ
c chuy
ể
n v
ị
trên biên c
ủ
a hình ph
ẳ
ng (H6.2)
a. Trên ph
ầ
n m
ặ
t biên cv, S
u:
cho tr
ướ
c các cv:
(
)
(
)
yxvvyxuu
bb
,;, == . (6.19)
b. Trên m
ặ
t biên ch
ị
u l
ự
c, S
T
(H6.3):
.sincos
;sincos
θσθτστ
θτθστσ
yxyyxy
b
y
xyxxyx
b
x
mlT
mlT
+=+=
+=+=
(6.20)