
Lý Thuyết Đàn Hồi
52
Chương IV
VẬT LIỆU - ĐNNH LUẬT HOOKE TỔNG QUÁT - THẾ NĂNG BIẾN DẠNG
Lý thuyết ứng suất và Lý thuyết biến dạng cho phép thu được ba hệ phương trình cơ bản của Lý
thuyết đàn hồi, bao gồm:
• 3 phương trình cân bằng (2.16);
• 3 quan hệ biến dạng-chuyển vị (3.14);
• 6 quan hệ tương thích (3.23).
Đây là những phương trình nghiệm đúng cho mọi môi trường liên tục, không phụ thuộc gì vào tính
chất cơ học của vật liệu mô hình tính toán. Hệ 3 phương trình đầu tiên thực chất là các phương trình cân
bằng về hình chiếu, còn điều kiện cân bằng về momen dẫn đến các quan hệ tương đồng ứng suất tiếp, mà
nhờ đó số thành phần ứng suất chưa, biết độc lập nhau, giảm từ 9 xuống còn 6. Trong 6 phương trình
tương thích, thực chất, cũng chỉ có 3 phương trình độc lập nhau. Như vậy là, trong tổng số 15 phương
trình cơ bản chỉ có 9 phương trình là độc lập nhau, và như vậy, không đủ cho tổng số 15 Nn số (bao gồm 6
tành phần ứng suất, 6 thành phần biến dạng và 3 thành phần chuyển vị) của bài toán đàn hồi . Điều này
cũng dễ hiểu vì, cho đến lúc này, ta chưa hề xem xét gì đến tính chất cơ học của mô hình khảo sát, cụ thể
là về cách thức ứng xử của vật liệu mô hình dưới tác dụng của lực ngoài. Các phương trình còn thiếu nói
trên sẽ được bổ sung nhờ việc khảo sát đặc tính cơ học của vật liệu mô hình.
§4.1 Đặc trưng cơ học của vật liệu
Ứng xử cơ học của vật liệu thường được mô tả bởi quan hệ giữa ứng suất và biến dạng. Một cách
tổng quát, ứng suất là hàm của biến dạng, của tỉ số giữa các biến dạng, của tiến trình biến dạng, tốc độ
biến dạng, nhiệt độ và của đặc trưng vật liệu. Tuy nhiên, ta chỉ chọn mô hình tương đối đơn giản, là mô
hình vật thể đàn hồi liên tục, không đề cập đến các yếu tố tốc độ, của tiến trình biến dạng... Có thể hình
dung mô hình này như một môi trường bị biến dạng một cách liên tục khi chịu lực tác dụng và bao giờ
cũng sẽ trở về với cấu hình ban đầu của nó khi các lực tác dụng bị dỡ bỏ. Về sau ta còn giả thiết thêm rằng
quan hệ giữa ứng suất và biến dạng là tuyến tính. Tuy các giả thiết này đã đơn giản hóa đáng kể mô hình
nghiên cứu nhưng chúng lại phù hợp với các số liệu thực nghiệm và là cơ sở cho nhiều phương pháp ứng
dụng trong phân tích kết cấu. Với điều kiện biến dạng bé, nhiều vật liệu kết cấu thực tế như: kim loại, chất
dẻo, gỗ, đá, bêtông cót thép, …. luôn tuân thủ qui tắc tuyến tính trong quan hệ giữa ứng suất và biến
dạng.
Như đã nêu trên, việc xác định tính chất cơ học của vật liệu thực tế thường được tiến hành theo con
đường thực nghiệm. Một trong những kỹ thuật thí nghiệm truyền thống là kỹ thuật kéo đơn giản mẫu thí
nghiệm hình trụ hoặc hình dẹt (H4.1), chịu tải trọng theo một trục (đơn trục), trên các thiết bị kéo.
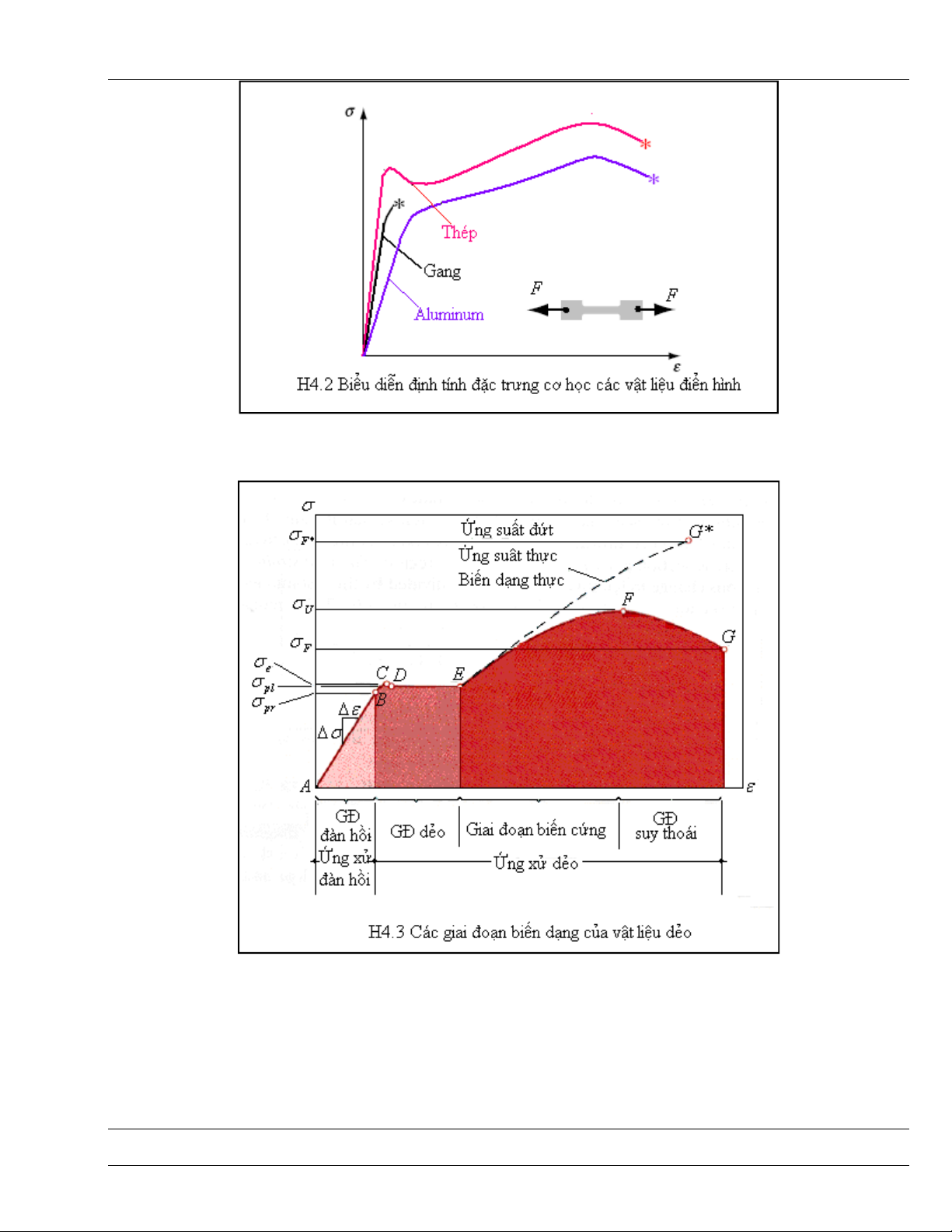
Kết quả nghiên cứu thực nghiệm đối với ba loại vật liệu điển hình (thép carbon thường, nhôm và
gang) được giới thiệu trên H4.2. Thép và nhôm có tính dẻo nên mẫu thử có khả năng chịu biến dạng lớn
còn gang thì dòn và do đó mẫu thử bị đứt ngay khi biến dạng còn chưa lớn mấy. Có thể nhận xét thấy,
trong giai đoạn đầu, khi biến dạng còn là bé, ứng xử của các vật liệu là tuyến tính. Giai đoạn tiếp theo có
ứng xử phi tuyến, thường là tương ứng với biến dạng lớn.
(Thiếu hình 4.1: Hai mẫu thử kéo)
Lý Thuyết Đàn Hồi
53
Với vật liệu dẻo, quá trình biến dạng (đã lý tưởng hóa) được thể hiện trên hình H4.3.
Điểm kết thúc của giai đoạn tuyến tính gọi là giới hạn tỉ lệ. Trong giai đoạn ứng xử đàn hồi, nếu bỏ lực tác
dụng ngoài, vật thể trở về với cấu hình không biến dạng ban đầu và khi đó, không còn biến dạng. Điểm
bắt đầu của giai đoạn ứng xử không đàn hồi của vật liệu gọi là giới hạn đàn hồi. Với nhiều loại vật liệu,
giới hạn đàn hồi và giới hạn tỉ tệ là khác nhau, tuy nhiên, một cách gần đúng có thể coi hai giới hạn này là
như nhau. Điểm dẻo là một điểm khác trên đường cong quan hệ ứng suất-biến dạng, là điểm bắt đầu biến
dạng dẻo lớn (H4.3).

Lý Thuyết Đàn Hồi
54
§4.2 Định luật Hooke tổng quát.
Từ các phân tích ở đầu chương ta thấy rằng, trạng thái ứng suất và biến dạng của vật thể không thể
mô tả được chỉ nhờ các phương trình cơ bản, đã dẫn ra trên đây. Cụ thể là, để xác định 6 thành phần của
tensơ ứng suất, 6 thành phần của tensor biến dạng và 3 thành phần chuyển vị, với tổng cộng là 15 Nn, hiện
chỉ có 9 phương trình độc lập nhau. Vì thế cho nên, để giải quyết các bài toán Lý thuyết đàn hồi, cần xác
định thêm quan hệ giữa ứng suất và biến dạng của vật liệu mô hình tính toán. Nếu như điều này được thực
hiện, có thể biểu diễn, chẳng hạn như, các thành phần ứng suất trong 3 phương trình cân bằng (2.16) qua
các thành phần biến dạng, rồi dùng (3.14) chuyển các thành phần biến dạng qua 3 thành phần chuyển vị u,
v, w và bằng cách này, có thể thay 3 phương trình (2.16) bằng 3 phương trình vi phân chứa 3 hàm chưa
biết là các chuyển vị u, v và w. Vai trò của các phương trình tương thích (3.23) cùng với các điều kiện
biên sẽ là các điều kiện mà nghiệm của bài toán đàn hồi phải thỏa mãn.
Ta sẽ khảo sát vật thể đàn hồi có tính chất đặc biệt là công tiêu tốn làm biến dạng nó không phụ
thuộc vào cách thức thực hiện các chuyển vị của các điểm từ trạng thái đầu đến trạng thái cuối của sự
biến dạng. Vì thế cho nên, khi bỏ đi tải trọng đã gây ra biến dạng của vật thể, vật thể sẽ trở về trạng thái
không biến dạng ban đầu và toàn bộ công tiêu tốn cho quá trình biến dạng trước đó sẽ được hoàn trả đầy
đủ. Vật thể có tính chất nói trên được gọi là vật thể đàn hồi lý tưởng. Vật thể đàn hồi mà quan hệ giữa các
thành phần ứng suất và các thành phần biến dạng là tuyến tính, được gọi là vật thể đàn hồi tuyến tính.
Trên thực tế tồn tại những vật liệu có tính chất đàn hồi lý tưởng nhưng không phải là tuyến tính. Định luật
xác lập quan hệ tuyến tính giữa các thành phần ứng suất và các thành phần biến dạng là tuyến tính có tên
là Định luật Hooke. Định luật có tầm quan trọng hết sức to lớn này đã được Rober Hooke (Anh) và E.
Maroitte (Pháp) đặt nền móng đầu tiên khi, một cách độc lập nhau, hai ông phát hiện ra sự phụ thuộc tỉ lệ
thuận giữa các đại lượng mà ngày nay chúng ta gọi là ứng suất và biến dạng, vào giữa thế kỷ 18 (chính
xác hơn là vào năm 1860).
Biểu thức toán học (dưới dạng vô hướng) của định luật Hooke nêu ra trên đây là như sau:
.
;
;
;
;
;
666564636261
565554535251
464544434241
363534333231
262524232221
161514131211
zxyzxyzyxx
zxyzxyzyxyz
zxyzxyzyxxy
zxyzxyzyxz
zxyzxyzyxy
zxyzxyzyxx
cccccc
cccccc
cccccc
cccccc
cccccc
cccccc
γγγεεετ
γγγεεετ
γγγεεετ
γγγεεεσ
γγγεεεσ
γγγεεεσ
+++++=
+++++=
+++++=
+++++=
+++++=
+++++=
(4.1)
Đả
o l
ạ
i, có th
ể
bi
ể
u di
ễ
n các thành ph
ầ
n bi
ế
n d
ạ
ng theo các thành ph
ầ
n
ứ
ng su
ấ
t nh
ư
sau
.
;
;
;
;
;
666564636261
565554535251
464544434241
363534333231
262524232221
161514131211
zxyzxyzyxzx
zxyzxyzyxyz
zxyzxyzyxxy
zxyzxyzyxx
zxyzxyzyxy
zxyzxyzyxx
aaaaaa
aaaaaa
aaaaaa
aaaaaa
aaaaaa
aaaaaa
τττσσσγ
τττσσσγ
τττσσσγ
τττσσσε
τττσσσε
τττσσσε
+++++=
+++++=
+++++=
+++++=
+++++=
+++++=
(4.2)
trong
đ
ó, các h
ệ
s
ố
aij có th
ể
bi
ể
u di
ễ
n qua các h
ệ
s
ố
cij. Các quan h
ệ
(4.1) và (4.2) chính là các bi
ể
u th
ứ
c
c
ủ
a
đị
nh lu
ậ
t Hooke t
ổ
ng quát (vi
ế
t d
ướ
i d
ạ
ng vô h
ướ
ng).
D
ướ
i d
ạ
ng ma tr
ậ
n, có th
ể
bi
ể
di
ễ
n (4.1) và (4.2) nh
ư
sau:
{
}
[
]
{
}
ε
σ
c
=
(4.1*)
{
}
[
]
{
}
σ
ε
a
=
(4.2*)
trong
đ
ó,

Lý Thuy
ế
t
Đ
àn H
ồ
i
55
{
}
[
]
T
zxyzxyzyx
τττσσσσ
=; (4.3)
{
}
[
]
T
zxyzxyzyx
γγγεεεε
=; (4.4)
[
]
[
]
61 ;61 , ÷=÷−= jicc
ij
; (4.5)
[
]
[
]
61 ;61 , ÷=÷−= jiaa
ij
. (4.6)
T
ừ
(4.1) và (4.2) ta có:
[
]
[
]
1−
=ac
(4.7)
Các h
ệ
s
ố
aij và cij , trong (4.1) và (4.2),
đặ
c tr
ư
ng cho tính ch
ấ
t
đ
àn h
ồ
i c
ủ
a v
ậ
t th
ể
t
ạ
i
đ
i
ể
m kh
ả
o
sát và không ph
ụ
thu
ộ
c gì vào giá tr
ị
c
ủ
a các thành ph
ầ
n bi
ế
n d
ạ
ng ho
ặ
c c
ủ
a các thành ph
ầ
n
ứ
ng su
ấ
t.
Các h
ệ
s
ố
này
đượ
c g
ọ
i là các h
ằ
ng s
ố
(module)
đ
àn h
ồ
i. N
ế
u nh
ư
các h
ệ
s
ố
aij và cij không ph
ụ
thu
ộ
c vào
to
ạ
độ
c
ủ
a
đ
i
ể
m trên v
ậ
t th
ể
, thì v
ậ
t th
ể
đượ
c g
ọ
i là
đồ
ng nh
ấ
t (ho
ặ
c
đồ
ng ch
ấ
t). V
ề
sau, ta s
ẽ
ch
ỉ
kh
ả
o sát
v
ậ
t th
ể
đồ
ng ch
ấ
t.
Ma tr
ậ
n
ứ
ng su
ấ
t và ma tr
ậ
n bi
ế
n d
ạ
ng c
ủ
a v
ậ
t th
ể
đ
àn h
ồ
i tuy
ế
t tính là
đ
ói x
ứ
ng, t
ứ
c các h
ệ
s
ố
trong các quan (4.1) và (4.2) ph
ả
i th
ỏ
a mãn tính ch
ấ
t t
ươ
ng
đồ
ng nh
ư
sau:
jiij
cc =
(4.8)
và
jiij
aa =
(4.9)
Bên c
ạ
nh tính
đồ
ng ch
ấ
t, m
ộ
t tính ch
ấ
t c
ơ
b
ả
n khác c
ủ
a v
ậ
t li
ệ
u là tính
đị
nh h
ướ
ng. Tính
đị
nh h
ướ
ng
ph
ả
n
ả
nh s
ự
khác nhau c
ủ
a các
đặ
c tr
ư
ng
đ
àn h
ồ
i theo các h
ướ
ng khác nhau (c
ủ
a h
ệ
t
ọ
a
độ
). M
ộ
t s
ố
v
ậ
t
li
ệ
u nh
ư
pha lê, g
ỗ
, composite có các module
đ
àn h
ồ
i khác nhau theo các h
ướ
ng khác nhau.
Đ
ó là nh
ữ
ng
v
ậ
t li
ệ
u d
ị
h
ướ
ng. Tuy nhiên v
ớ
i
đ
a s
ố
các v
ậ
t li
ệ
u k
ỹ
thu
ậ
t nh
ư
thép, h
ợ
p kim nhôm và
đ
a ph
ầ
n các ch
ấ
t
d
ẻ
o có c
ấ
u trúc vi mô tinh th
ể
v
ớ
i
đị
nh h
ướ
ng phân b
ố
m
ộ
t cách ng
ẫ
u nhiên khi
ế
n cho các tính ch
ấ
t
đ
àn
h
ồ
i v
ĩ
mô c
ủ
a chúng là nh
ư
nhau theo các h
ướ
ng. Các lo
ạ
i v
ậ
t li
ệ
u này
đượ
c g
ọ
i là
đẳ
ng h
ướ
ng.
Các công th
ứ
c (4.1) ch
ứ
a 36 h
ằ
ng s
ố
đ
àn h
ồ
i, tuy nhiên, không ph
ả
i t
ấ
t c
ả
chúng là
độ
c l
ậ
p nhau.
Để
xác l
ậ
p quan h
ệ
gi
ữ
a các h
ằ
ng s
ố
đ
àn h
ồ
i ta hãy
đề
c
ậ
p
đế
n m
ộ
t khái ni
ệ
m quan tr
ọ
ng,
đ
ó là th
ế
n
ă
ng
bi
ế
n d
ạ
ng.
§4.3 Thế năng biến dạng đàn hồi
D
ướ
i tác d
ụ
ng c
ủ
a các l
ự
c m
ặ
t và l
ự
c kh
ố
i, v
ậ
t th
ể
đ
àn h
ồ
i b
ị
bi
ế
n d
ạ
ng. Trong quá trình bi
ế
n d
ạ
ng
này, các l
ự
c nói trên th
ự
c hi
ệ
n công c
ơ
h
ọ
c. N
ế
u quá trình bi
ế
n d
ạ
ng là ch
ậ
m, không kèm theo các hi
ệ
u
ứ
ng quán tính và không phát nhi
ệ
t thì, trên c
ơ
s
ở
c
ủ
a nguyên lý b
ả
o toàn n
ă
ng l
ượ
ng, toàn b
ộ
công này
đượ
c tích l
ũ
y vào v
ậ
t th
ể
d
ướ
i d
ạ
ng th
ế
n
ă
ng bi
ế
n d
ạ
ng. V
ớ
i v
ậ
t th
ể
đ
àn h
ồ
i, khi b
ỏ
l
ự
c ngoài, toàn b
ộ
th
ế
n
ă
ng này
đượ
c hoàn tr
ả
tr
ọ
n v
ẹ
n. Công và th
ế
n
ă
ng là các khái ni
ệ
m h
ế
t s
ứ
c quan tr
ọ
ng mà nh
ờ
s
ử
d
ụ
ng
chúng m
ớ
i có th
ể
có
đượ
c nh
ữ
ng thông tin b
ổ
ích c
ũ
ng nh
ư
các qui t
ắ
c và ph
ươ
ng pháp h
ữ
u hi
ệ
u trong
viêc gi
ả
i quy
ế
t các bài toán c
ơ
h
ọ
c v
ậ
t th
ể
bi
ế
n d
ạ
ng nói chung và các bài toán
đ
àn h
ồ
i nói riêng. Có th
ể
nói, khái ni
ệ
m n
ă
ng l
ượ
ng (công và th
ế
n
ă
ng)
đ
ã t
ạ
o ra cách nhìn m
ớ
i, m
ộ
t c
ơ
s
ở
m
ớ
i
để
gi
ả
i các bài toán
đ
àn h
ồ
i c
ũ
ng nh
ư
cho phép có
đượ
c nhi
ề
u l
ờ
i gi
ả
i m
ớ
i,
ư
u vi
ệ
t h
ơ
n, cho nhi
ề
u v
ấ
n
đề
đ
ã
đượ
c gi
ả
i quy
ế
t
tr
ướ
c
đ
ây b
ằ
ng các công c
ụ
khác. Trong th
ờ
i gian g
ầ
n
đ
ây, các ph
ươ
ng pháp d
ự
a trên khái ni
ệ
m n
ă
ng
l
ượ
ng (có tên chung là các ph
ươ
ng pháp n
ă
ng l
ượ
ng)
đ
ã
đượ
c v
ậ
n d
ụ
ng h
ế
t s
ứ
c r
ộ
ng rãi trong vi
ệ
c phát
tri
ể
n các ph
ươ
ng pháp ph
ầ
n t
ử
biên c
ũ
ng nh
ư
ph
ươ
ng pháp ph
ầ
n t
ử
h
ữ
u h
ạ
n. D
ướ
i
đ
ây ta ch
ỉ
có th
ể
th
ả
o
lu
ậ
n m
ộ
t cách ng
ắ
n g
ọ
n v
ề
đề
tài nói trên mà thôi.
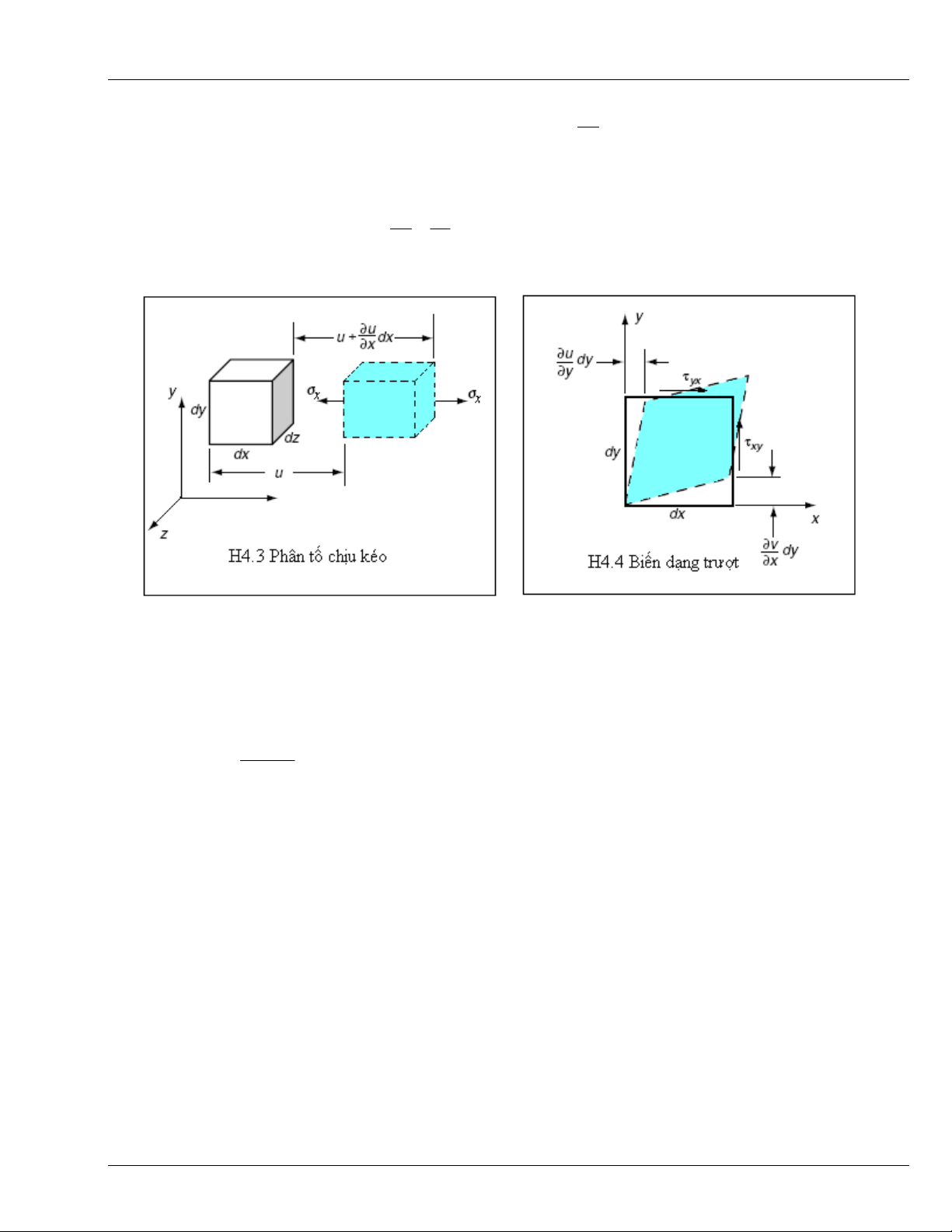
Xét m
ộ
t phân t
ố
hình kh
ố
i ch
ữ
nh
ậ
t, có các c
ạ
nh dx, dy, dz vô cùng ng
ắ
n, trong v
ậ
t th
ể
đ
àn h
ồ
i, cân
b
ằ
ng d
ướ
i tác d
ụ
ng c
ủ
a các l
ự
c ngoài. Gi
ả
s
ử
trên b
ề
m
ặ
t phân t
ố
này ch
ỉ
t
ồ
n t
ạ
i thành ph
ầ
n
ứ
ng su
ấ
t
σ
x
phân b
ố
đề
u, còn các thành ph
ầ
n
ứ
ng su
ấ
t khác
đề
u b
ằ
ng 0.
Đồ
ng th
ờ
i, c
ũ
ng không t
ồ
n t
ạ
i các l
ự
c kh
ố
i
(H4.3).
Lý Thuy
ế
t
Đ
àn H
ồ
i
56
Khi l
ự
c tác d
ụ
ng lên phân t
ố
σ
xdydz
đượ
c b
ổ
sung m
ộ
t l
ượ
ng d(
σ
xdydz), thì các c
ạ
nh cùng ph
ươ
ng
v
ớ
i tr
ụ
c x c
ủ
a hình kh
ố
i phân t
ố
s
ẽ
có
độ
giãn dài b
ổ
sung
dxddx
x
u
d
x
ε
=
==
=
∂
∂∂
∂
∂
∂∂
∂
)(
. Công (phân t
ố
) c
ủ
a l
ự
c tác
d
ụ
ng
σ
xdydz lên hình h
ộ
p, l
ấ
y chính xác
đế
n
đạ
i l
ượ
ng bé c
ấ
p 2, b
ằ
ng dxdydzd
xx
εσ
.
N
ế
u gi
ả
thi
ế
t r
ằ
ng trên m
ặ
t bên c
ủ
a hình h
ộ
p phân t
ố
ch
ỉ
tác d
ụ
ng c
ủ
a
ứ
ng su
ấ
t c
ắ
t
τ
xy (H4.4), thì,
c
ũ
ng v
ớ
i l
ậ
p lu
ậ
n nh
ư
trên, l
ư
u ý là xy
x
v
y
u
γ
=
∂
∂
+
∂
∂, có th
ể
thu
đượ
c bi
ể
u th
ứ
c gia s
ố
công do
ứ
ng l
ự
c c
ắ
t
gây ra:
dxdydzd
xyxy
γτ
Khi phân t
ố
ch
ị
u tác d
ụ
ng c
ủ
a t
ấ
t c
ả
các thành ph
ầ
n
ứ
ng su
ấ
t, gia s
ố
công s
ẽ
b
ằ
ng t
ổ
ng công do
t
ừ
ng
ứ
ng l
ự
c thành ph
ầ
n (t
ươ
ng
ứ
ng v
ớ
i các thành ph
ầ
n
ứ
ng su
ấ
t) t
ạ
o ra:
[
]
,dxdydzdddddddA
zxzxyzyzxyxyzzyyxx
γτγτγτεσεσεσ
+++++=
(4.10)
và công cho m
ộ
t
đơ
n v
ị
th
ể
tích s
ẽ
là:
.
zxzxyzyzxyxyzzyyxx
dddddd
dxdydz
dA
dW
γτγτγτεσεσεσ
+++++==
(4.11)
Trên c
ơ
s
ở
c
ủ
a công th
ứ
c (4.11) có th
ể
coi các thành ph
ầ
n
ứ
ng su
ấ
t và các thành ph
ầ
n bi
ế
n d
ạ
ng là các
l
ự
c suy r
ộ
ng và các chuy
ể
n v
ị
suy r
ộ
ng t
ươ
ng
ứ
ng, theo
đị
nh ngh
ĩ
a quen thu
ộ
c c
ủ
a khái ni
ệ
m này.
Ta gi
ả
thi
ế
t r
ằ
ng quá trình bi
ế
n d
ạ
ng x
ả
y ra ch
ậ
m và v
ớ
i nhi
ệ
t
độ
không
đổ
i,
đồ
ng th
ờ
i,
toàn b
ộ
công tiêu t
ố
n cho s
ự
bi
ế
n d
ạ
ng
đề
u t
ậ
p trung vào vi
ệ
c làm t
ă
ng th
ế
n
ă
ng c
ủ
a v
ậ
t th
ể
. Khi
đ
ó,
công th
ứ
c (4.11) chính là công th
ứ
c xác
đị
nh th
ế
n
ă
ng c
ủ
a
đơ
n v
ị
th
ể
tích v
ậ
t th
ể
. C
ầ
n l
ư
u ý m
ộ
t
đ
i
ề
u là
khi thi
ế
t l
ậ
p các công th
ứ
c (4.10) và (4.11) ta không c
ầ
n vi
ệ
n d
ẫ
n
đế
n m
ộ
t tính ch
ấ
t v
ậ
t lý xác
đị
nh nào
c
ủ
a v
ậ
t th
ể
, do
đ
ó, chúng nghi
ệ
m
đ
úng cho m
ọ
i v
ậ
t th
ể
liên t
ụ
c.
Có th
ể
ch
ứ
ng minh
đượ
c r
ằ
ng, công
đơ
n v
ị
th
ể
tích c
ủ
a các l
ự
c n
ộ
i l
ự
c không ph
ụ
thu
ộ
c vào vi
ệ
c ch
ọ
n
h
ướ
ng c
ủ
a h
ệ
to
ạ
độ
, ngh
ĩ
a là có th
ể
vi
ế
t
.
'''''''''''''''''' xzxzzyzyyxyxzzyyxx
zxzxyzyzxyxyzzyyxx
dddddd
dddddd
γτγτγτεσεσεσ
γ
τ
γ
τ
γ
τ
ε
σ
ε
σ
ε
σ
+++++=
=
+
+
+
+
+
(4.12)
trong
đ
ó,
'''''''''
, , , , ,
xzzyyxzyx
τττσσσ
và
'''''''''
,,,,,
xzzyyxzyx
γγγεεε
- là các thành ph
ầ
n
ứ
ng su
ấ
t và các
thành ph
ầ
n bi
ế
n d
ạ
ng trong h
ệ
t
ọ
a
độ
(x’,y’, z’).


![Bài tập tối ưu trong gia công cắt gọt [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251129/dinhd8055/135x160/26351764558606.jpg)













