
Lý Thuy
ế
t
Đ
àn H
ồ
i
70
Ch
ươ
ng V
THI
Ế
T L
Ậ
P BÀI TOÁN LÝ THUY
Ế
T
Đ
ÀN H
Ồ
I
§5.1 Các phương trình cơ sở tổng quát của lý thuyết đàn hồi
Tr
ạ
ng thái v
ậ
t lý t
ạ
i
đ
i
ể
m v
ậ
t ch
ấ
t trên v
ậ
t th
ể
đ
àn h
ồ
i
đượ
c xác
đị
nh b
ở
i các
đạ
i l
ượ
ng: 6 thành ph
ầ
n
ứ
ng su
ấ
t, 6 thành ph
ầ
n bi
ế
n d
ạ
ng và 3 thành ph
ầ
n chuy
ể
n v
ị
. Các
đạ
i l
ượ
ng nói trên
đượ
c g
ọ
i là các bi
ế
n
c
ơ
b
ả
n c
ủ
a bài toán lý thuy
ế
t
đ
àn h
ồ
i. Các bi
ế
n c
ơ
b
ả
n t
ạ
i m
ộ
t
đ
i
ể
m bên trong v
ậ
t th
ể
ph
ả
i ch
ị
u s
ự
ràng
bu
ộ
c b
ở
i các quan h
ệ
đ
ã
đượ
c thi
ế
t l
ậ
p
đượ
c t
ừ
các ch
ươ
ng II, ch
ươ
ng III và ch
ươ
ng IV, bao g
ồ
m:
•
h
ệ
các ph
ươ
ng trình cân b
ằ
ng:
.0
;0
;0
=+
∂
∂
+
∂
∂
+
∂
∂
=+
∂
∂
+
∂
∂
+
∂
∂
=+
∂
∂
+
∂
∂
+
∂
∂
z
z
yz
xz
y
zyyxy
x
zx
yx
x
F
zyz
F
zyx
F
zyx
σ
τ
τ
τστ
τ
τ
σ
(5.1)
•
các quan h
ệ
ứ
ng su
ấ
t-bi
ế
n d
ạ
ng :
;
;
;
z
w
y
v
x
u
z
y
x
∂
∂
=
∂
∂
=
∂
∂
=
ε
ε
ε
.
2
1
;
2
1
;
2
1
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
=
∂
∂
+
∂
∂
=
x
w
z
u
z
v
y
w
y
u
x
v
zx
yz
xy
γ
γ
γ
(5.2)
•
h
ệ
ph
ươ
ng trình các t
ươ
ng thích:
;2
;2
;2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
x
z
e
z
e
x
e
zy
e
y
e
z
e
yx
e
x
e
y
e
zxx
z
yz
z
y
xyy
x
∂∂
∂
=
∂
∂
+
∂
∂
∂∂
∂
=
∂
∂
+
∂
∂
∂∂
∂
=
∂
∂
+
∂
∂
.
;
;
2
2
2
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
=
∂∂
∂
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
=
∂∂
∂
∂
∂
+
∂
∂
+
∂
∂
−
∂
∂
=
∂∂
∂
y
e
x
e
z
e
xyx
e
x
e
z
e
y
e
yxz
e
z
e
y
e
x
e
xzy
e
zx
yzxy
z
yzxy
zx
y
xy
zx
yz
x
(5.3)
•
đị
nh lu
ậ
t Hooke t
ổ
ng quát:
.
;
;
;
;
;
666564636261
565554535251
464544434241
363534333231
262524232221
161514131211
zxyzxyzyxx
zxyzxyzyxyz
zxyzxyzyxxy
zxyzxyzyxz
zxyzxyzyxy
zxyzxyzyxx
cccccc
cccccc
cccccc
cccccc
cccccc
cccccc
γγγεεετ
γγγεεετ
γγγεεετ
γγγεεεσ
γγγεεεσ
γγγεεεσ
+++++=
+++++=
+++++=
+++++=
+++++=
+++++=
(5.4).
Trong 6 ph
ươ
ng trình t
ươ
ng thích (5.3) trên
đ
ây, ch
ỉ
có 3 ph
ươ
ng trình
độ
c l
ậ
p nhau và là các
đ
i
ề
u ki
ệ
n
c
ầ
n và
đủ
để
cho các thành ph
ầ
n chuy
ể
n v
ị
là
đơ
n tr
ị
và liên t
ụ
c (cho v
ậ
t th
ể
đơ
n liên), khi các thành ph
ầ
n
bi
ế
n d
ạ
ng xác
đị
nh tr
ướ
c.
Các ph
ươ
ng trình trên
đ
ây
đượ
c g
ọ
i là các ph
ươ
ng trình c
ơ
s
ở
chung c
ủ
a lý thuy
ế
t
đ
àn h
ồ
i. V
ề
th
ự
c
ch
ấ
t, các ph
ươ
ng trình c
ơ
s
ở
chung bao g
ồ
m 15 ph
ươ
ng trình vi phân và các quan h
ệ
đạ
i s
ố
,
độ
c l
ậ
p nhau,
gi
ữ
a các thành ph
ầ
n
ứ
ng su
ấ
t, các tp bi
ế
n d
ạ
ng và các tp chuy
ể
n v
ị
.
Để
hoàn t
ấ
t vi
ệ
c thi
ế
t l
ậ
p bài toán còn
ph
ả
i thi
ế
t l
ậ
p các
đ
i
ề
u ki
ệ
n biên. Các
đ
i
ề
u ki
ệ
n biên
đượ
c xác
đị
nh tùy theo
đ
i
ề
u ki
ệ
n v
ậ
t lý, hình h
ọ
c t
ạ
i
t
ừ
ng
đ
i
ể
m trên m
ặ
t bao v
ậ
t th
ể
kh
ả
o sát. Trong khi các ph
ươ
ng trình c
ơ
s
ở
là nh
ư
nhau thì các
đ
i
ề
u ki
ệ
n

Lý Thuy
ế
t
Đ
àn H
ồ
i
71
biên l
ạ
i khác nhau, tùy thu
ộ
c vào t
ừ
ng bài toán.
Để
có
đượ
c l
ờ
i gi
ả
i c
ủ
a các bài toán, c
ầ
n bi
ế
t cách xác
đị
nh
đ
úng các
đ
i
ề
u ki
ệ
n biên. Các ph
ươ
ng trình c
ơ
s
ở
k
ế
t h
ợ
p v
ớ
i các
đ
i
ề
u ki
ệ
n biên s
ẽ
hình thành các bài
toán giá tr
ị
biên c
ơ
b
ả
n (g
ọ
i t
ắ
t là bài toán biên) c
ủ
a lý thuy
ế
t
đ
àn h
ồ
i. Có hai hình th
ứ
c bài toán biên
th
ườ
ng g
ặ
p,
đ
ó là: bài toán theo chuy
ể
n v
ị
và bài toán theo
ứ
ng su
ấ
t. Vì, nói chung, r
ấ
t khó tìm l
ờ
i gi
ả
i c
ủ
a
bài toán biên nên
đ
ã có khá nhi
ề
u các chi
ế
n thu
ậ
t gi
ả
i quy
ế
t v
ấ
n
đề
đượ
c
đề
ra ph
ụ
c v
ụ
cho m
ụ
c
đ
ích này.
Tr
ướ
c khi th
ả
o lu
ậ
n v
ề
các bài toán biên c
ơ
b
ả
n, ta th
ả
o lu
ậ
n thêm v
ề
các
đ
i
ề
u ki
ệ
n biên và cách xác
đị
nh
đ
úng các
đ
i
ề
u ki
ệ
n biên. Ph
ầ
n cu
ố
i ch
ươ
ng nêu ra các chi
ế
n thu
ậ
t th
ườ
ng s
ử
d
ụ
ng và gi
ớ
i thi
ệ
u các
nguyên lý t
ổ
ng quát
đượ
c
ứ
ng d
ụ
ng r
ộ
ng rãi khi gi
ả
i quy
ế
t các bài toán lý thuy
ế
t
đ
àn h
ồ
i. Các quan h
ệ
đề
c
ậ
p
đế
n trong ch
ươ
ng này và v
ề
sau ch
ủ
y
ế
u
đượ
c mô t
ả
d
ướ
i d
ạ
ng vô h
ướ
ng ho
ặ
c ma tr
ậ
n.
§5.2 Điều kiện biên
N
ế
u nh
ư
các giá tr
ị
các bi
ế
n bên trong v
ậ
t th
ể
ch
ỉ
ch
ị
u s
ự
ràng bu
ộ
c c
ủ
a các ph
ươ
ng trình c
ơ
s
ở
thì
các bi
ế
n c
ơ
b
ả
n t
ạ
i các
đ
i
ể
m trên m
ặ
t biên còn ph
ả
i tuân th
ủ
thêm các các
đ
i
ề
u ki
ệ
n biên. V
ề
m
ặ
t v
ậ
t lý,
các
đ
i
ề
u ki
ệ
n biên ph
ả
n
ả
nh t
ươ
ng tác trên biên gi
ữ
a v
ậ
t th
ể
v
ớ
i môi tr
ườ
ng còn v
ề
m
ặ
t toán h
ọ
c, các
đ
i
ề
u
ki
ệ
n biên k
ế
t h
ợ
p v
ớ
i các ph
ươ
ng trình cân b
ằ
ng t
ạ
o
để
nên các bài toán biên hoàn ch
ỉ
nh. Thông th
ườ
ng,
đ
i
ề
u ki
ệ
n biên cho bi
ế
t v
ậ
t th
ể
đượ
c gi
ữ
cân b
ằ
ng trong không gian b
ằ
ng cách nào và ch
ị
u tác d
ụ
ng th
ế
nào t
ừ
các
đố
i t
ượ
ng bên ngoài. Các
đ
i
ề
u ki
ệ
n này
đượ
c xác
đị
nh, v
ề
m
ặ
t toán h
ọ
c, thông qua vi
ệ
c ch
ỉ
đị
nh (cho bi
ế
t tr
ướ
c) các chuy
ể
n v
ị
ho
ặ
c l
ự
c m
ặ
t t
ạ
i các
đ
i
ể
m trên m
ặ
t bao v
ậ
t th
ể
. N
ế
u ký hi
ệ
u b
ề
m
ặ
t cho
tr
ướ
c chuy
ể
n v
ị
là S
u
(g
ọ
i t
ắ
t là m
ặ
t biên chuy
ể
n v
ị
) còn b
ề
m
ặ
t cho tr
ướ
c l
ự
c m
ặ
t, (m
ặ
t biên l
ự
c), là S
T
thì
b
ề
m
ặ
t toàn b
ộ
c
ủ
a v
ậ
t th
ể
, S , b
ằ
ng t
ổ
ng c
ủ
a m
ặ
t biên chuy
ể
n v
ị
và m
ặ
t biên l
ự
c: S = S
u
+ S
T
. N
ế
u
chuy
ể
n v
ị
bi
ế
t tr
ướ
c là b
ằ
ng 0, thì m
ặ
t biên
đượ
c g
ọ
i là biên c
ố
đị
nh. N
ế
u trên m
ặ
t biên không có l
ự
c tác
d
ụ
ng và chuy
ể
n v
ị
c
ũ
ng không bi
ế
t tr
ướ
c, ta có
đ
i
ề
u ki
ệ
n biên t
ự
do.
Nói chung, trên m
ỗ
i m
ặ
t biên t
ồ
n t
ạ
i m
ộ
t
đ
i
ề
u ki
ệ
n biên: ho
ặ
c là biên l
ự
c ho
ặ
c là biên chuy
ể
n v
ị
.
Tuy nhiên, theo hai h
ướ
ng khác nhau trên cùng m
ộ
t m
ặ
t biên có th
ể
t
ồ
n t
ạ
i
đ
i
ề
u ki
ệ
n biên chuy
ể
n v
ị
theo
h
ướ
ng này và
đ
i
ề
u ki
ệ
n biên l
ự
c còn theo h
ướ
ng kia. Trong ví d
ụ
v
ề
t
ấ
m ch
ữ
nh
ậ
t ch
ị
u kéo
đố
i x
ứ
ng trên
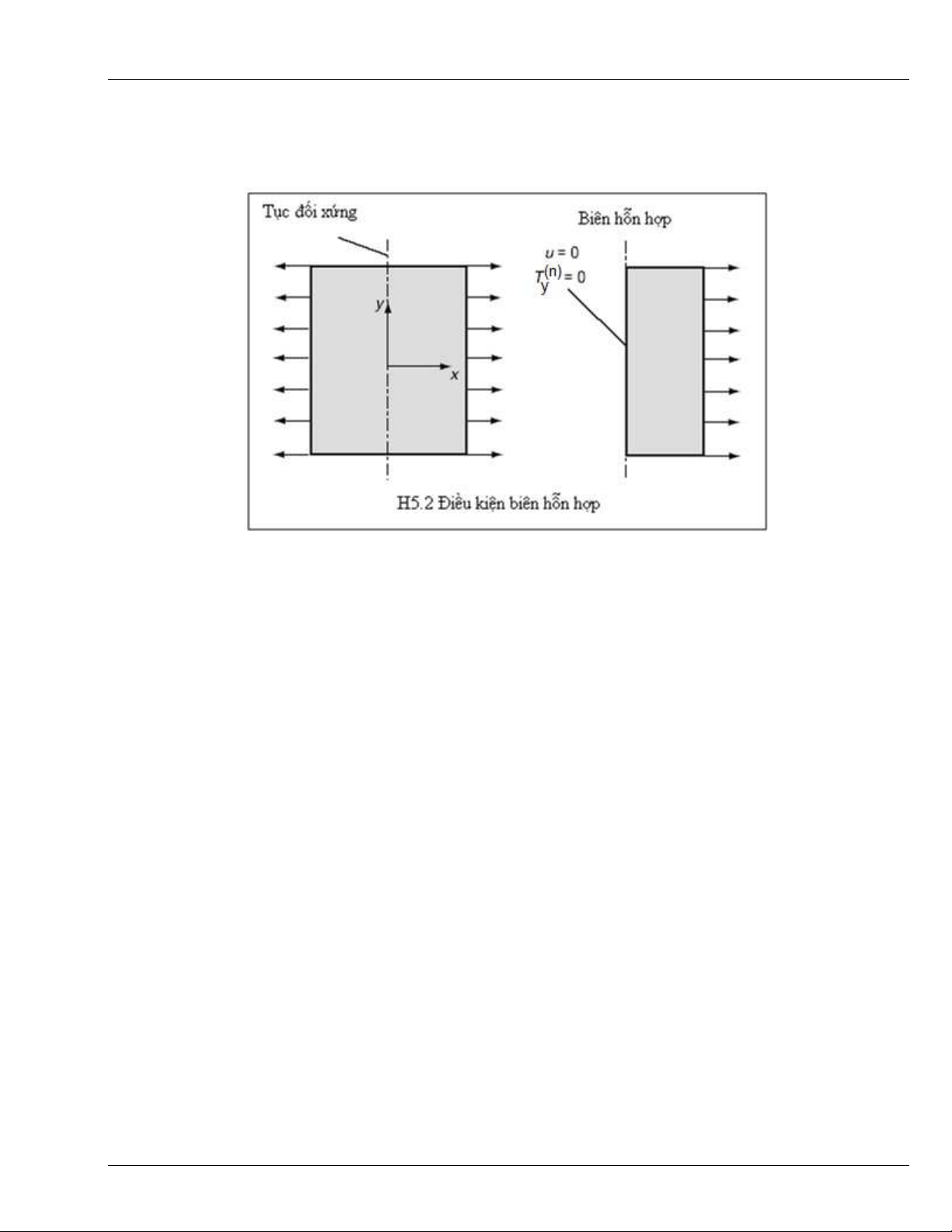
hình H5.2, hai c
ạ
nh song song v
ớ
i tr
ụ
c y là các biên l
ự
c, còn hai c
ạ
nh kia là các biên không ch
ị
u l
ự
c, c
ũ
ng
v
ẫ
n thu
ộ
c lo
ạ
i biên l
ự
c. Tuy nhiên, n
ế
u s
ử
d
ụ
ng tính ch
ấ
t
đố
i x
ứ
ng c
ủ
a bài toán, ch
ỉ
c
ầ
n kh
ả
o sát m
ộ
t n
ử
a
t
ấ
m, nh
ư
trên hình, và tr
ụ
c
đố
i x
ứ
ng tr
ở
thành m
ộ
t "biên". Các
đ
i
ể
m trên tr
ụ
c
đố
i x
ứ
ng không có chuy
ể
n
v
ị
đườ
ng theo ph
ươ
ng x (là
đ
i
ề
u ki
ệ
n biên chuy
ể
n v
ị
) và không ch
ị
u l
ự
c m
ặ
t (là
đ
i
ề
u ki
ệ
n biên không ch
ị
u
l
ự
c) theo ph
ươ
ng y, do
đ
ó, tr
ụ
c
đố
i x
ứ
ng v
ừ
a là biên l
ự
c v
ừ
a là biên chuy
ể
n v
ị
. T
ấ
t nhiên các y
ế
u t
ố
chuy
ể
n v
ị
và l
ự
c c
ủ
a lo
ạ
i
đ
i
ề
u ki
ệ
n biên này ph
ả
i t
ươ
ng
ứ
ng v
ớ
i nhau.
Thi
ế
t l
ậ
p các
đ
i
ề
u ki
ệ
n biên là b
ướ
c r
ấ
t quan tr
ọ
ng trong quá trình l
ậ
p bài toán và gi
ả
i quy
ế
t bài toán
lý thuy
ế
t
đ
àn h
ồ
i. Vi
ệ
c xác
đị
nh sai các
đ
i
ề
u ki
ệ
n biên có th
ể
bi
ế
n bài toán này thành bài toán khác ho
ặ
c
làm cho l
ờ
i gi
ả
i sai l
ệ
ch và nhi
ề
u khi là không gi
ả
i
đượ
c. K
ỹ
n
ă
ng thi
ế
t l
ậ
p
đ
úng các
đ
i
ề
u ki
ệ
n biên c
ầ
n
đượ
c rèn luy
ệ
n k
ỹ
thông qua th
ự
c hành gi
ả
i các bài t
ậ
p.
Lý Thuy
ế
t
Đ
àn H
ồ
i
72
Vi
ệ
c xác l
ậ
p
đ
i
ề
u ki
ệ
n biên chuy
ể
n v
ị
có th
ể
th
ự
c hi
ệ
n m
ộ
t cách tr
ự
c ti
ế
p và, nói chung, là
đơ
n gi
ả
n
h
ơ
n so v
ớ
i
đ
i
ề
u ki
ệ
n biên l
ự
c. Vi
ệ
c áp
đặ
t
đ
i
ề
u ki
ệ
n biên l
ự
c t
ạ
i m
ộ
t
đ
i
ể
m trên biên có ngh
ĩ
a là áp
đặ
t
đ
i
ề
u
ki
ệ
n cân b
ằ
ng c
ủ
a t
ứ
di
ệ
n phân t
ố
t
ạ
i
đ
i
ể
m nói trên (xem
§
2.2). D
ự
a trên k
ế
t qu
ả
thu
đượ
c t
ừ
ch
ươ
ng II,
đ
i
ề
u ki
ệ
n cân b
ằ
ng c
ủ
a t
ứ
di
ệ
n phân t
ố
đượ
c bi
ể
u di
ễ
n (d
ướ
i d
ạ
ng vô h
ướ
ng) b
ở
i ph
ươ
ng trình
:
,
;
;
zzyyzxxz
n
x
zzyyyxxy
n
y
zzxyyxxx
n
x
nnnT
nnnT
nnnT
σττ
τστ
ττσ
++=
++=
++=
(5.5)
trong
đ
ó,
zyx
nnn ,,
là các cosine ch
ỉ
ph
ươ
ng pháp tuy
ế
n ngoài c
ủ
a
đ
i
ể
m trên biên trong h
ệ
t
ọ
a
độ
kh
ả
o sát;
n
z
n
y
n
x
TTT ,,
là các thành ph
ầ
n c
ủ
a vector l
ự
c m
ặ
t
đơ
n v
ị
t
ạ
i
đ
i
ể
m kh
ả
o sát;
zxyzxyzyx
τττσσσ
,,,,,
là các thành ph
ầ
n
ứ
ng su
ấ
t t
ạ
i
đ
i
ể
m kh
ả
o sát.
Công th
ứ
c (5.5) cho th
ấ
y,
để
th
ỏ
a mãn
đ
i
ề
u ki
ệ
n cân b
ằ
ng trên biên, l
ự
c m
ặ
t
đơ
n v
ị
ph
ả
i có quan h
ệ
xác
đị
nh v
ớ
i các thành ph
ầ
n
ứ
ng su
ấ
t t
ạ
i các
đ
i
ể
m trên biên. Vi
ệ
c xác l
ậ
p
đ
i
ề
u ki
ệ
n biên l
ự
c cho m
ộ
t bài
toán c
ụ
th
ể
chính là vi
ệ
c xác
đị
nh các cosine ch
ỉ
ph
ươ
ng
zyx
nnn ,,
cùng v
ớ
i các thành ph
ầ
n l
ự
c m
ặ
t
n
z
n
y
n
x
TTT ,,
t
ạ
i các
đ
i
ể
m trên biên
để
t
ừ
đ
ó xác l
ậ
p
đượ
c các quan h
ệ
d
ạ
ng (5.5), mà các thành ph
ầ
n
ứ
ng
su
ấ
t t
ạ
i
đ
i
ể
m trên biên ph
ả
i th
ỏ
a mãn.
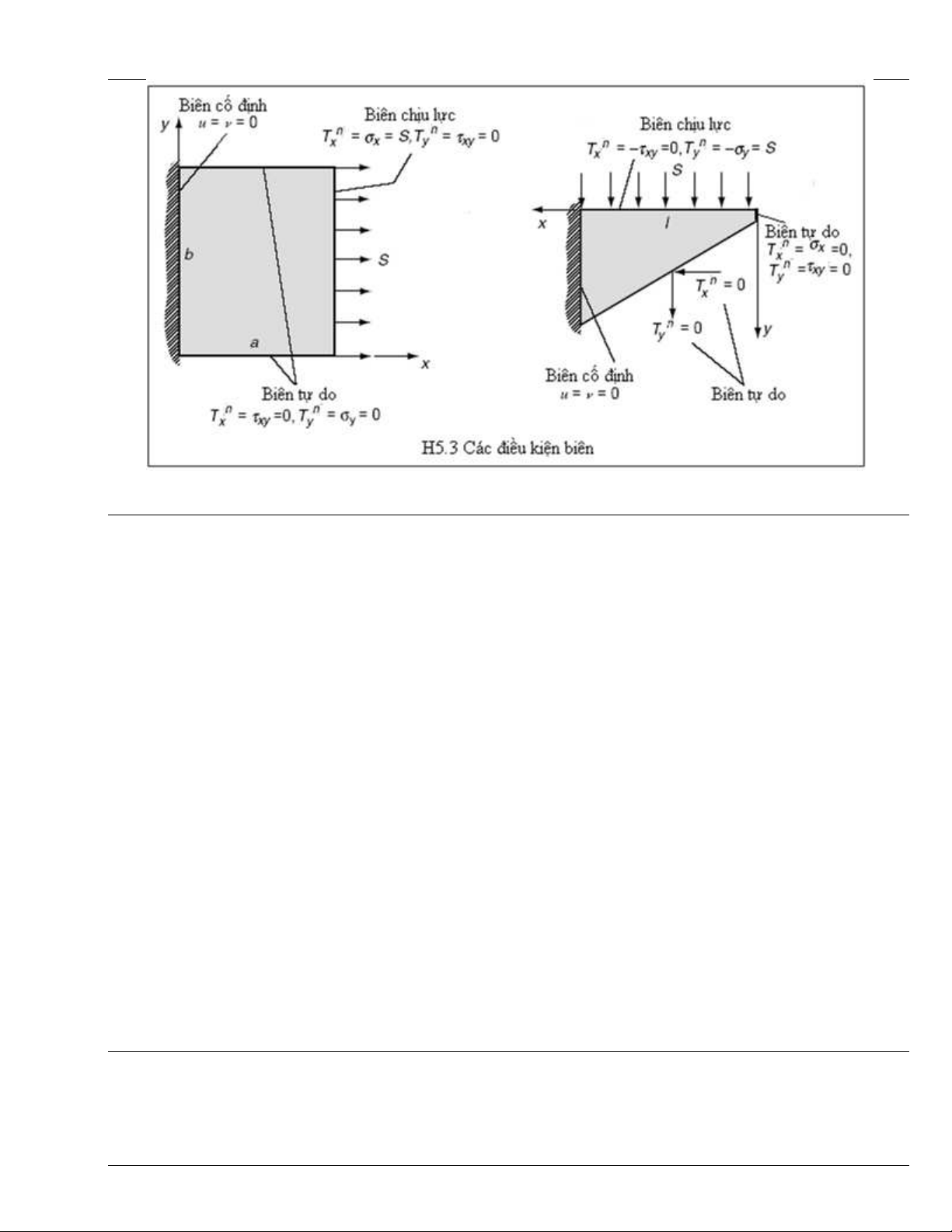
H5.3 là các ví d
ụ
đơ
n gi
ả
n, c
ụ
th
ể
v
ề
các
đ
i
ề
u ki
ệ
n biên.
Lý Thuy
ế
t
Đ
àn H
ồ
i
73
§5.3 Các bài toán biên
Gi
ả
i m
ộ
t bài toán lý thuy
ế
t
đ
àn h
ồ
i c
ụ
th
ể
là vi
ệ
c xác
đị
nh phân b
ố
ứ
ng su
ấ
t, bi
ế
n d
ạ
ng và \ ho
ặ
c
chuy
ể
n v
ị
th
ỏ
a mãn các ph
ươ
ng trình c
ơ
s
ở
(5.1) cùng các
đ
i
ề
u ki
ệ
n biên c
ụ
th
ể
c
ủ
a bài toán. Nh
ư
trên
đ
ây
đ
ã
đề
c
ậ
p
đế
n, các ph
ươ
ng trình c
ơ
s
ở
k
ế
t h
ợ
p v
ớ
i m
ộ
t lo
ạ
i
đ
i
ề
u ki
ệ
n biên xác
đị
nh s
ẽ
hình thành m
ộ
t bài
toán giá tr
ị
biên t
ươ
ng
ứ
ng. Ta g
ọ
i t
ắ
t bài toán giá tr
ị
biên là bài toán biên. Có 3 bài toán biên biên c
ơ
b
ả
n,
đượ
c xác
đị
nh nh
ư
sau:
1.
Bài toán biên lực
: Xác
đị
nh s
ự
phân b
ố
c
ủ
a các
ứ
ng su
ấ
t, chuy
ể
n v
ị
và bi
ế
n d
ạ
ng t
ạ
i các
đ
i
ể
m trên
v
ậ
t th
ể
đ
àn h
ồ
i cân b
ằ
ng khi cho tr
ướ
c các l
ự
c kh
ố
i và s
ự
phân b
ố
c
ủ
a các l
ự
c tác d
ụ
ng lên b
ề
m
ặ
t
đượ
c mô t
ả
b
ở
i:
(
)
(
)
S
ij
S
i
n
j
xfxT =
(5.6)
trong
đ
ó,
S
i
x
bi
ể
u th
ị
đ
i
ể
m trên m
ặ
t biên (ch
ị
u l
ự
c) còn
(
)
S
ij
xf
bi
ể
u th
ị
giá tr
ị
c
ủ
a l
ự
c m
ặ
t t
ạ
i
đ
i
ể
m
trên biên nói trên.
2.
Bài toán biên chuyển vị
: Xác
đị
nh s
ự
phân b
ố
c
ủ
a các
ứ
ng su
ấ
t, chuy
ể
n v
ị
và bi
ế
n d
ạ
ng t
ạ
i các
đ
i
ể
m trên v
ậ
t th
ể
đ
àn h
ồ
i cân b
ằ
ng khi cho tr
ướ
c các l
ự
c kh
ố
i và s
ự
phân b
ố
c
ủ
a chuy
ể
n v
ị
trên b
ề
m
ặ
t
đượ
c mô t
ả
b
ở
i:
(
)
(
)
S
ij
S
ij
xgxu =
(5.7)
trong
đ
ó,
S
i
x
bi
ể
u th
ị
đ
i
ể
m trên m
ặ
t biên (ch
ị
u l
ự
c) còn
(
)
S
ij
xg
bi
ể
u th
ị
giá tr
ị
c
ủ
a chuy
ể
n v
ị
t
ạ
i
đ
i
ể
m trên biên nói trên.
3.
Bài toán biên hỗn hợp
: Xác
đị
nh s
ự
phân b
ố
c
ủ
a các
ứ
ng su
ấ
t, chuy
ể
n v
ị
và bi
ế
n d
ạ
ng t
ạ
i các
đ
i
ể
m
trên v
ậ
t th
ể
đ
àn h
ồ
i cân b
ằ
ng khi cho tr
ướ
c các l
ự
c kh
ố
i và s
ự
phân b
ố
c
ủ
a các l
ự
c tác d
ụ
ng lên b
ề
m
ặ
t
ch
ị
u l
ự
c S
T
đượ
c mô t
ả
b
ở
i (5.6) và s
ự
phân b
ố
c
ủ
a chuy
ể
n v
ị
trên b
ề
m
ặ
t S
u
đượ
c mô t
ả
b
ở
i (5.7).
§5.4 Tính duy nhất nghiệm của bài toán biên
Ta xét bài toán v
ớ
i
đ
i
ề
u ki
ệ
n biên h
ỗ
n h
ợ
p, t
ứ
c t
ồ
n t
ạ
i
đồ
ng th
ờ
i c
ả
m
ặ
t biên cv, S
u
l
ẫ
n m
ặ
t biên
ch
ị
u l
ự
c S
T
. Tính ch
ấ
t duy nh
ấ
t nghi
ệ
m bài toán gía tr
ị
biên
đượ
c ch
ứ
ng minh b
ằ
ng ph
ươ
ng pháp ph
ả
n
ch
ứ
ng. Gi
ả
s
ử
t
ồ
n t
ạ
i
đồ
ng th
ờ
i nghi
ệ
m phân bi
ệ
t nhau hai:
(
)
(
)
(
)
{
}
111
iijij
ue
σ
và
(
)
(
)
(
)
{
}
222
iijij
ue
σ
, cho

Lý Thuy
ế
t
Đ
àn H
ồ
i
74
cùng m
ộ
t bài toán v
ớ
i l
ự
c m
ặ
t, l
ự
c kh
ố
i c
ũ
ng nh
ư
các
đ
i
ề
u ki
ệ
n biên h
ệ
t nh
ư
nhau. Hi
ệ
u c
ủ
a hai nghi
ệ
m
trên
đượ
c bi
ể
u di
ễ
n b
ở
i:
(
)
(
)
( ) ( )
( ) ( )
.
;
'
21
21
21
iii
ijijij
ijijij
uuu
eee
−=
−=
−=
σσσ
(5.8)
Vì hai nghi
ệ
m (1) và (2) th
ỏ
a mãn
đ
i
ề
u ki
ệ
n cân b
ằ
ng v
ớ
i cùng m
ộ
t l
ự
c kh
ố
i nh
ư
nhau nên hi
ệ
u c
ủ
a chúng
s
ẽ
ph
ả
i th
ỏ
a mãn
đ
i
ề
u ki
ệ
n cân b
ằ
ng không l
ự
c kh
ố
i, t
ứ
c:
0
,
=
jij
σ
(5.9)
C
ũ
ng nh
ư
v
ậ
y, hi
ệ
u hai nghi
ệ
m s
ẽ
ph
ả
i th
ỏ
a mãn
đ
i
ề
u ki
ệ
n biên 0, t
ứ
c
đ
i
ề
u ki
ệ
n không có l
ự
c m
ặ
t trên m
ặ
t
ch
ị
u l
ự
c S
T
c
ũ
ng nh
ư
không có chuy
ể
n v
ị
trên m
ặ
t biên cv, hay:
0==
jij
n
i
nT
σ
trên S
T
(5.10)
và c
ả
đ
i
ề
u ki
ệ
n không chuy
ể
n v
ị
trên biên chuy
ể
n v
ị
S
u
: 0=
i
u trên S
u
(5.11)
Ta có th
ể
bi
ế
n
đổ
i bi
ể
u th
ứ
c th
ế
n
ă
ng v
ậ
t th
ể
ứ
ng tr
ạ
ng thái hi
ệ
u c
ủ
a hai nghi
ệ
m nh
ư
sau:
(
)
( )
∫∫
∫∫ ∫
∫∫∫
−=
−==
−==
V
ijij
S
ijij
V
ijij
V V
iijjiij
V
ijjiij
V
ijij
V
dVudSun
dVudVudVu
dVudVeWdV
,
,,
,
2
σσ
σσσ
ωσσ
(5.12)
trong
đ
ó,
(
)
ijjiij
uu
,,
2
1−=
ω
là tensor xoay [xem công th
ứ
c (3.8)m
ụ
c
§
3.1].
Để
có k
ế
t qu
ả
trên,
đ
ã v
ậ
n
d
ụ
ng
đị
nh lý divergent
để
chuy
ể
n tích phân trên th
ể
tích v
ề
tích phân m
ặ
t t
ươ
ng
ứ
ng. Ngoài ra, c
ầ
n nh
ớ
r
ằ
ng ngo
ạ
i tích c
ủ
a m
ộ
t tensor
đố
i x
ứ
ng v
ớ
i m
ộ
t tensor ph
ả
n x
ứ
ng luôn b
ằ
ng 0, nên có
0=
ijij
ωσ
. V
ớ
i l
ư
u
ý r
ằ
ng m
ặ
t biên bao g
ồ
m hai ph
ầ
n: biên ch
ị
u l
ự
c và biên cv, t
ứ
c
uT
SSS += , trên c
ơ
s
ở
(5.9)÷(5.12) ta
có
02 =
∫
V
WdV . (5.13)
Vì th
ế
n
ă
ng W là hàm xác
đị
nh d
ươ
ng nên t
ừ
(5.13) ta có
0
=
W
trên toàn mi
ề
n V và t
ừ
đ
ó, suy ra r
ằ
ng
các thành ph
ầ
n
ứ
ng su
ấ
t và các thành ph
ầ
n bi
ế
n d
ạ
ng
đề
u tri
ệ
t tiêu, t
ứ
c
0==
ijij
e
σ
, trên toàn mi
ề
n. Vì
0=
ij
e
trên toàn mi
ề
n nên v
ậ
t kh
ả
o sát không b
ị
bi
ế
n d
ạ
ng mà ch
ỉ
có th
ể
chuy
ể
n v
ị
nh
ư
v
ậ
t r
ắ
n. Nh
ư
ng vì
trên biên chuy
ể
n v
ị
ph
ả
i th
ỏ
a mãn
đ
i
ề
u ki
ệ
n 0=
i
u nên suy ra r
ằ
ng, chuy
ể
n v
ị
c
ũ
ng tri
ệ
t tiêu, t
ứ
c, 0=
i
u
trên toàn mi
ề
n V. Nói cách khác, hai nghi
ệ
m cho tr
ướ
c ph
ả
i
đồ
ng nh
ấ
t, hay, nghi
ệ
m bài toán là duy nh
ấ
t.
L
ư
u ý r
ằ
ng, n
ế
u nh
ư
không t
ồ
n t
ạ
i m
ặ
t biên chuy
ể
n v
ị
thì
(
)
1
i
u
và
(
)
2
i
u
sai khác nhau b
ở
i chuy
ể
n v
ị
c
ủ
a v
ậ
t
r
ắ
n.
§5.4 Dạng chuyển vị và dạng ứng suất của các phương trình cơ sở chung
Vi
ệ
c tìm l
ờ
i gi
ả
i b
ấ
t k
ỳ
m
ộ
t trong 3 bài toán biên trên
đ
ây
đề
u h
ế
t s
ứ
c ph
ứ
c t
ạ
p.
Để
ph
ụ
c v
ụ
cho vi
ệ
c
tìm các l
ờ
i gi
ả
i này, ta ti
ế
p t
ụ
c rút g
ọ
n, bi
ế
n
đổ
i các ph
ươ
ng trình c
ơ
s
ở
(5.1)÷(5.4) v
ề
d
ạ
ng thích h
ợ
p v
ớ
i
t
ừ
ng bài toán biên nêu trên. Các ph
ươ
ng trình c
ơ
s
ở
(5.1)÷(5.4) ch
ứ
a 15
N
n s
ố
c
ơ
b
ả
n, bao g
ồ
m các thành
ph
ầ
n
ứ
ng su
ấ
t, các thành ph
ầ
n bi
ế
n d
ạ
ng và các thành ph
ầ
n chuy
ể
n v
ị
. B
ằ
ng cách s
ử
d
ụ
ng
đị
nh lu
ậ
t Hooke
để
bi
ể
u di
ễ
n các thành ph
ầ
n
ứ
ng su
ấ
t và dùng quan h
ệ
ứ
ng su
ấ
t- bi
ế
n d
ạ
ng lo
ạ
i tr
ừ
các thành ph
ầ
n bi
ế
n
d
ạ
ng, ta thu
đượ
c h
ệ
3 ph
ươ
ng trình ch
ỉ
v
ớ
i 3
N
n s
ố
là các thành ph
ầ
n chuy
ể
n v
ị
.
Đ
ó là d
ạ
ng chuy
ể
n v
ị
c
ủ
a các ph
ươ
ng trình c
ơ
s
ở
. D
ạ
ng chuy
ể
n v
ị
c
ủ
a các ph
ươ
ng trình c
ơ
s
ở
chung
đượ
c s
ử
d
ụ
ng r
ấ
t r
ộ
ng rãi
và
đặ
c bi
ệ
t thích h
ợ
p cho các bài toán biên chuy
ể
n v
ị
, khi mà các
đ
i
ề
u ki
ệ
n biên ch
ỉ
ch
ứ
a chuy
ể
n v
ị
. M
ộ
t


![Bài tập tối ưu trong gia công cắt gọt [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251129/dinhd8055/135x160/26351764558606.jpg)













